Численный алгоритм расчета температурных полей пневматических шин в процессе вулканизации

Вулканизация многоэлементных изделий сложной конфигурации, например покрышек, представляет собой сложнейший вариант теплового процесса [1]. Расчет температурных полей в вулканизируемом изделии, теплофизические характеристики которого зависят от температуры, является одной из наиболее важных задач теплофизики. Решение этой задачи позволяет моделировать процессы вулканизации изделий с целью неразрушающего контроля их качества, рассчитывать продолжительность процессов в широком диапазоне температур и оптимумов вулканизации с учетом теплофизических свойств и геометрических параметров объектов. [2].

Произведем постановку задачи. В качестве математической модели процесса вулканизации рассмотрим систему уравнений теплового баланса вида:

C k P k 8 T ( t , x ) / d t — V Л ⁽ Т ) V T ⁽ t , x ^)] + q k ⁽ t , x ) , x e V _k , k =1,2,^, K ;                                (1)

где c _k , p _k , Л _к ( т ) соответственно удельная теплоемкость, плотность, теплопроводность k-го слоя; T ( t , x ) , q_k ( t , x ) - температура и плотность тепловыделения в точке x к -го слоя в момент времени t: q k ( t , x ) — q T • exp [ E k " ( Т ( t , x ) - T . ) / ( R • T ( t , x ) • T . ) ] , q k"* - суммарное количество тепла, выделяемое в в к -м слое; Е_к - энергия активации процесса вулканизации к- го слоя; R - универсальная газовая постоянная; T - эквивалентная температура, к которой приводятся результаты неизотермической вулканизации [1-5].

Систему уравнений (1) дополним:

- начальными условиями:

Т ( 0, x ) — Т _о,                   (2)

В (5), (6) x 'e V_k , x" e V_{k + 1} , x e S _{k + 2} , S k +2 -поверхность контакта смежных слоёв V k и V k +1 , n -вектор нормали к S k +2 ; k =1,2,..., К -1; K - количество разнородных материалов, входящих в расчетную модель.

Зависимость теплопроводности от температуры будем аппроксимировать линейными функциями вида:

Л ( Т ) = a k — b k • Т ,               (7)

где a _k , b _k - константы.

Величину энергии активации определим по данным контрольных испытаний образцов смеси, полученных при изотермических условиях вулканизации (рисунок 1):

_ ( Т 2 + 273,15 ) - ( Т 1 + 273,15 )     t "

Е —--1П — , k             т - т              t',

где t - время достижения максимального значения динамического модуля М ( t ) при температуре Т 1 ; t ”- время достижения максимального значения динамического модуля М ( t ) при температуре Т 2 .

Степень завершенности процесса вулканизации X ( t ) в точке x k -го слоя в момент вре-

мени t будем оценивать по формуле:

X ( t ) =

M ( t. ( t )) - M о

M

max

^{- M} 0

где t ₃ ( t ) - эквивалентное время вулканизации

при температуре T 1 =190 °С :

t э

t

( t ) — /

E k

R e

Т + 273,15 Т ( т ) + 273,15

d T ,

M(t ) - текущее, M_o , M_max - соответственно,

минимальное и максимальное значение динамического модуля М при T 1 =190 °С (рисуник 1), Т ( т ) - текущее значение температуры в точке

где Т - начальная температура, которая зависит от времени года и соответствует температуре в сборочном цехе;

• -    граничными условиями:

Т ( t , x ) — Ф 1 ( t , x ) , x e S 1 ;           (3)

T ( t , x ) — ^ , ( t , x ) , x e S 2 ,          (4)

где S 1 - поверхность контакта пресс-форма-теплоноситель, S 2 - поверхность контакта диафрагма-теплоноситель;

• -    контактными условиями в точках, принадлежащим поверхностям соприкосновения разнородных слоев:

lim T ( t , x ') — lim T ( t , x "),            (5)

lim Л ( T ( t , x ’ )) d T ( t , x’ ) / d n —

— lim A _{k + 1} ( T ( t , x'' )) d T ( t , x” ) / d n .           (6)

x' ' ^ x

x в момент времени т в °С .

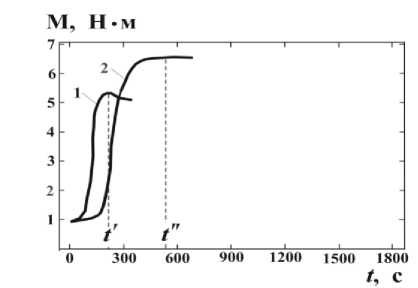
Рисунок 1. Кинетика вулканизации k -го слоя по экспериментальным данным, полученным с помощью реометра. 1-график зависимости динамического модуля М ( t ) от времени при температуре T 1 =190 °С; 2-график М ( t ) при температуре T 2 =170 °С

Далее приведено решение системы уравнений (1)-(6). Введем в рассмотрение функции Л _к ( т ) , определенные следующим

T образом: Лк(т) = J Хк (г dk

T 0

Тогда система уравнений теплопроводности (1) примет вид:

скрк дT (t, x) / дt = А Л к (t, x) + qk (t, x), x e Vk, где А = V2 - оператор Лапласа, Лк (t, x) = Лк (т(t, x)).

Начальное условие (2) примет вид:

Л к (0, x )= 0, ^=1,2,.,K.(10)

Граничные условия (3), (4) примут вид:

Л(t,x) = Л(1)(t,x), x e Sx;(11)

Л(t,x) = Л(2)(t,x), x e S2,(12)

где Л ^{( 1 )} ( t , x ) = Л m ( ф 1 ( t , x )) , m - номер слоя, граница

Решение системы уравнений (10)-(15) будем осуществлять с помощью метода их конечно-разностной аппроксимации на системе точек { t ⁽ m ) , x j j, где t ⁽ m ) = t ⁽ m ^{- 1 )} + А t ; t ^{( 0 )} = 0 ; m = 1,2,...,M_t , А t - шаг дискретизации по времени, x j,₁ =^r _J ,„h ji) , i = 1,2,..., ^ ; j = 1,2,... K , . Точки x ,, , , x ₂ , i ,^, x^ ; i =1,2,..., N расположены на отрезках [ x _t,, x_K._it ], x, _t e S ,, x_{K i} e S ₂ (рисунок 3).

которого в точке x совпадает с S ; Л ^{( 2} ) ( t , x ) =Л n ( ф ₂ ( t , x )) , n - номер слоя, граница которого в точке x совпадает с S .

Контактные условия (5), (6) примут вид:

^{Л (} t , x )

x ^{e S}k + 2

=л ;+

x ^e S t + 2

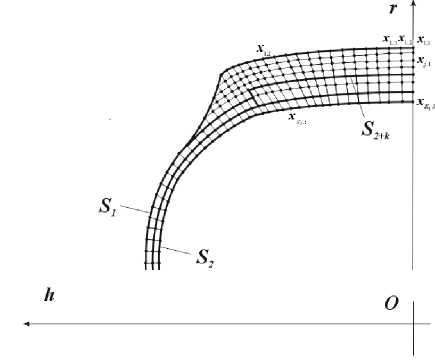
Рисунок 3. Расположение точек x j , i = ( r j -, ,, h j , _i )

^дЛ к ⁽ t , x )

^дЛ к + 1 ⁽ t , x )

д n

x ^e ^+ 2

д n

x ^e ^+ 2

Учитывая форму объекта моделирования, систему уравнений (9) удобно записать в цилиндрической системе координат (рисунок 2).

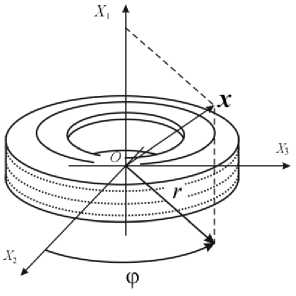
Рисунок 2. Объект моделирования

Выполним конечно-разностную аппроксимацию дифференциального оператора в правой части (15) в точке { t ^{( m} ) , x_b J.

Для этого перенесем начало системы координат Orh в точку x_]4 и выполним ее ортогональное вращение таким образом, чтобы ось O ' h ' новой системы координат O ' r ' h ' совпала с прямой, проходящей через точки x j _{+ 1} , i , x j , i , x j - 1,. (рисунок 4).

Введем обозначения:

Л_г , = дЛ / д r ', Л_г ,_г, = д ² Л / д r '² , Л_А , = дЛ / д h ', Л _h , _h , =д ² Л / д h ^,2, Л _r,_h, =д ² Л / д r ' / д h '.

Пренебрегая в первом приближении формой рисунка протектора, можно считать, что шина имеет осесимметрическую форму. Тогда система уравнений (9) будет иметь вид:

^{д т} ( t , r , h )_6^ _t ⁽ t , r , h ) ^{1 дЛ} к ( t , r , h ) ^дХ0 , r , h )

с^{к Р к}    д t    "    д r^{2    +} r    д r    ⁺    д h^{2    +} q ⁽ t ’ r ’

^{x (} r , h ^{) e} V ,                                      ⁽¹⁵⁾

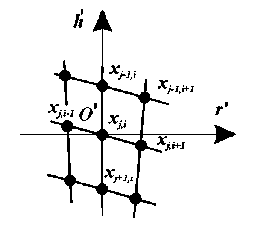
Рисунок 4. Расположение точек в системе координат O' r'h' .

где h = x 1 .

Разложим функцию Л_к( t . x ) в окрестности точки х_п в ряд Тейлора и, ограничившись членами второго порядка малости относительно A h j, A h j, получим систему уравнений для определения Л _h. . Л_h._h. :

|A h_x •Л h +A ^/2 •Л h.h ‘ = f .     ₍₁₆₎

| A h ₂ • Л_К + A h ₂ / 2 • Л _w = f ,

2     h       2          hh      2

где          Ah 1 = hj-1,i - h',,          Ah2 = hj+1,i - hj,i, f, =Л k (t(m). ^-Л k (t(m). x„), f2 =Л k (t(m), xj+1,)-Л k (t(m). x,,).

Аналогично, используя соответствующие разложения Л_к ( ⁽ m ) , x ) , получим систему уравнений для определения Л r . Л rr . Л rh, :

A r •Л r + A r • A h з • Л ry + A r ₃ ² / 2 • Л rr = f , ,

< A r ₄ •Л r +A r ₄ •A h ₄ •Л ry +A r ₄ ² /2 •Л _rV = f„            (17)

^{A r} ₅ •A _r, +^{A r} ₅ • ^A h ₅ •^Л ry + ^{A r} ₅ ² / ² •^Л rr = f . .

где ^A h з = h j - i, _{! +} i ^- j ,   ^{A r} з = r - i,i + i - r:i , ^A h 4 = h j , _{! +} i - h j . i,

AГ4 = rj.i+i - rj .i , Ah5 = hj,i-i - hj.i , AГ5 = rj.i-i - rj.i , f! =Лk(^ ^Xj-i,i +i)-Лk (^ ^Xj.i )-Ah3Лh'-Ah3 /2 •ЛKK , f, =Л k (t(m). xj.,+i )-Л k (t(m). xj., )- Ah4 •Л h-A42 /2 •Л hh, f, =Л k (t(m). xj., _i )-Л k (t(m), xj,, )-A h5 •Л h-Ah 52/2 •Л hh.

Учитывая     инвариантность     оператора

S²A_A. ( t , r , h ) 5²лД t , r , h )

—k    + —k      относительно переноса dr2           dh2

начала системы координат Orh и относительно ее ортогонального вращения, вокруг точки О'

получим:

дЛ _k ( t , r , h )   д ² Л _k ( t , r , h ) _ d ² A _k ( t , r ', h ')   d ² A _k ( t , r ', h ')

d r ²             d h ²     "      d r '²             d h' ²

. (18)

Соответственно:

dA _k ( t , r , h ) /d r = A _r. • n _i +Л _h , • n ₂ ,                 (19)

где n _i , n ₂ - направляющие косинусы вектора

Or в системе координат Or 'h' .

Таким образом, выражение для аппроксимации дифференциального оператора в правой части (15) будет иметь вид:

^д 2 ^{Л k (} t , r , h ) + ^ ^{дЛ k (} t , r , h ) + ^д 2 ^{Л k ( t} , r , h ) + q ( t , r , h ) » b,. Л_к ( t⁽m ) , x ,,) + d r ²        r d r           d h ²         ' j               J^

+ b ji+Ak ( t ⁽ m ) , x j , i + i ) + b j , _! - 1 Л k ( t ⁽ m ) , x j . i - i ) + b j - 1,₁ + 1 Л k ( t ⁽ m ) , x j - i. i + i ) + + b j - iAk ^{( t (} m ) . ^x j - i, ⁾⁺ b j + iAk ^{( t (} m ) . x j + i, ⁾⁺ 4 k ^{( t (} m ) . x j, ) где коэффициенты b_yi определяются п одстановкой вычисленных, путем решения систем уравнений (16), (17), значений Л _h, . Л _hh, , Л _r, . Л _r,_r, . Л _rh, в выражения (18), (19).

Учитывая, что Х_к ( T ) является медленно меняющейся функцией температуры, решение системы (10)-(15) во внутренних точках к -го слоя ( x _j . i е V _k \ 5 V_k ) при шаге дискретизации по времени:

^{A t} ^ c k P k ^{a 2/} ( ⁴ a k )              ⁽²⁰⁾

можно осуществить, используя явную разностную схему:

T ( t ( m ^{+ i )} . x j J= T ( t ( m ) . x j-i O+A t ( C k P k ) - ¹ [ b J , _! Л k ( t ( m ) . x j . _! ) +

+ b j, + 1 Л k ( t ⁽ m ) . x j, + i ) + b ,. , - 1 Л k ( t ⁽ m ) . x ji - i ) + b j - 1, _! + 1 Л k ( t ⁽ m ) . x j - ij + i ) + + b j - i.i Л k ( t ⁽ m ) . x j - i. , ) + b j + i^ k ( t ⁽ m ) . x j + i. i )₊ q k ( t ⁽ m ) . x j . , )] ,    (21)

где A - минимальное расстояние между точками xbt; ak -параметры аппроксимации теплопроводности к-го слоя. Для точек, принадлежащих поверхностям смежных слоев   (xj.i g Sk+2), аппроксимацию дифференциального оператора в (15) будем осуществлять по аналогичной схеме на основании метода баланса [6].

Приведем пример расчета. В примере выполнен расчет температурного поля для шины (рисунок 5), имеющей наружный диаметр -1,078 м и посадочный диаметр - 0,6096 м.

Значения удельной плотности и теплоемкости:

• -    для протектора p _i =1127; c_i =717;

• -    для брекера p =1106; с ₂ =641;

• -    для каркаса p =1071; с ₃ =615;

• -    для боковины р ₄=1134; с ₄ =663;

• -    для борта р =7700; с ₅ =460;

• - для наполнительного шнура р ₆ =1118; с ₆ =664.

Размерность величин р , к =1,2,_,5 дана в кг /м3 . Размерность величин c _k , k =1,2,_,5 дана в Дж/(кгтрад).

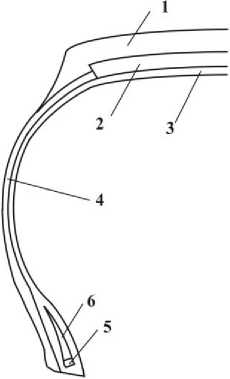
Рисунок 5. Конструкция пневматической шины.

1 - протектор; 2 - брекер; 3 - каркас; 4 - боковина;

5 - борт; 6 - наполнительный шнур

Параметры аппроксимации коэффициентов теплопроводности (7):

– для протектора a =0,1612; b =0,0002;

– для брекера a =0,1793; b =0,0003;

– для каркаса a =0,07; b =0,0;

– для боковины a =0,1941; b =0,0004;

– для борта a =50,0; b =0,0;

– для наполнительного шнура a =0,3426; b =0,0006.

Значения коэффициентов a , k =1,2,…,5 даны в Вт/ (м ·град) . Значения коэффициентов b , k =1,2,…,5 даны в Вт/ (м ·град· с).

При заданных начальных: T =20 °С и граничных:

0 1 ⁽ t , x ) = 0 2 ⁽ t , x ) =

150 °C,

20 °C,

при при

0 < t < 2700 c, t > 2700c условиях получено решение в виде изменения температурного поля во времени.

В таблице 1 приведены результаты расчетов, выполненных с разными значениями шага дискретизации по времени A t . Расчеты проводились в точках x , j =1,2,…,15.

Т а б л и ц а 1

Результаты расчетов температурного поля в момент времени t =1800 c, выполненные с разным значением A t

Номер точки	Значения шага дискретизации по времени A t , с
	8	4	2	1
1	150,0	150,0	150,0	150,0
2	149, 4	149,5	149,5	149,5
3	149,0	149,0	149 ,0	149,0
4	148, 6	148,5	148,5	148,5
5	148, 2	148, 2	148,1	148,1
6	147,9	147,9	147,9	147,9
7	147, 8	147,7	147,7	147,7
8	147, 7	147, 7	147,6	147,6
9	147, 8	147,7	147,7	147,7
10	147,8	147,8	147,8	147,8
11	148,0	148,0	148,0	148,0
12	148 ,4	148,4	148,4	148,4
13	148,9	148,9	148,9	148,9
14	149,4	149 ,4	149,4	149,4
15	150,0	150,0	150,0	150,0

Примечание. В таблице 1 подчеркнуты расхождения с результатами, выполненными с шагом дискретизации

A t =1 с

Результаты расчетов показывают устойчивую сходимость решения при уменьшении A t .

В таблице 2 приведены результаты расчетов, выполненные с разными значениями параметра A - минимального расстояния между точками x . С этой целью количество точек K i на отрезках [ x , x ] последовательно увеличивалось в 2, 4 и 8 раз. Величина A при этом уменьшалась соответственно 2, 4 и 8 раз.

Шаг дискретизации A t определялся в соответствии с условием (20). Значения температуры в таблице 2 рассчитаны для тех же точек, что и в таблице 1.

Т а б л и ц а 2

Результаты расчетов температурного поля в момент времени t =1800 c, выполненные с разным значением A

Номер точки	Значения A , м
	1,6×10-3	8,0×10-4	4,0×10-4	2,0×10-4
1	150,0	150,0	150,0	150,0
2	14 9 , 5	14 9 , 2	14 9 , 0	148,9
3	14 9 , 0	148, 4	148, 1	148,0
4	148, 5	147, 7	147, 3	147,1
5	14 8 , 1	14 7 , 7	146, 6	146,3
6	14 7 , 9	14 6 , 7	146, 0	145,7
7	14 7 , 7	14 6 , 4	145, 7	145,2
8	14 7 , 6	14 6 , 3	145, 5	145,0
9	14 7 , 7	14 6 , 3	145, 4	145,0
10	14 7 , 8	14 6 , 4	145, 6	145,2
11	14 8 ,0	14 6 , 8	14 6 , 1	145,7
12	14 8 ,4	14 7 , 3	146, 7	146,4
13	14 8 , 9	14 8 , 1	147, 6	147,4
14	14 9 , 4	148, 9	148, 7	148,6
15	150,0	150,0	150,0	150,0

Примечание. В таблице 2 подчеркнуты расхождения с результатами, выполненными с шагом дискретизации

A =2,0х10^-4 м.

Приведенные в таблице2 результаты показывают устойчивую сходимость решения с уменьшением величины A .

На рисунках 6-10 приведены распределения температуры и степени завершенности процесса X ( t ) (см. формулу (8)) в шине для различных значений времени.

Рисунок 6. Температура (в °С) в момент времени t =1800 c

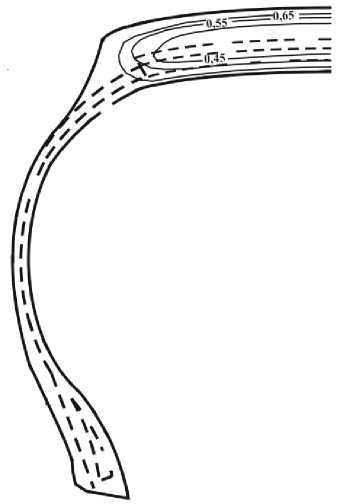
Рисунок 7. Степень завершенности процесса X ( t ) в момент времени t =1800 c

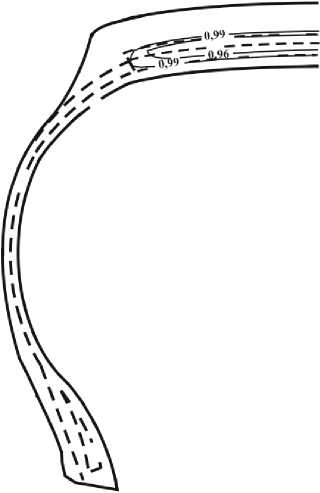
Рисунок 9. Степень завершенности процесса X ( t )

в момент времени t =3000 c

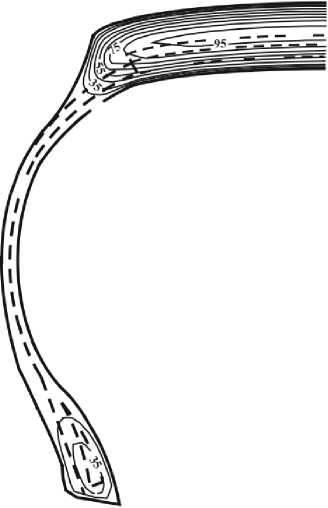
Рисунок 8. Температура (в °С) в момент времени t =3000 c

Рисунок 10. Температура (в °С) в момент времени t =3600 c

На момент времени t =3600 c степень завершенности процесса вулканизации во всех точках шины практически равна 1.

Заключение:

• 1)    рассмотрена математическая постановка задачи определения температурного поля в вулканизируемом изделии в условиях зависимости его теплофизических характеристик от температуры и с учетом заданных граничных и начальных условий;

• 2)    рассмотрен способ конечноразностной аппроксимации системы диффе-

• ренциальных уравнений теплопроводности, позволяющий учитывать сложную конфигурацию элементов вулканизируемого изделия, и получен численный алгоритм решения задачи;

• 3)    выполнены расчеты температурного поля для шины при заданных начальных и граничных значениях температуры;

• 4)    получены результаты, демонстрирующие устойчивость и точность решения;

• 5)    для различных моментов времени t выполнен расчет степени завершенности процесса вулканизации в изделии.

Вестник ВГУИТ, №2, 2015