Численный анализ автоколебаний активного фрактального осциллятора

В последнее время под влиянием возросшего интереса к естественнонаучным приложениям [1; 2] теории дробного интегродифференцирования [3] формируется новый раздел динамики – дробная динамика, или в англоязычном варианте – фрактальная динамика (fractional dynamics) [4]. Он охватывает исследования систем с интегродифференциальными уравнениями движения дробного порядка. Среди них одно из центральных мест, несомненно, принадлежит автоколебательным системам с фрактальными связями – активным фрактальным осцилляторам.

В работе [5] на основе схемы радиоэлектронного автогенератора с дробной цепью обратной связи введена в рассмотрение модель активного фрактального осциллятора (АФО). Предложенная нелинейная динамическая система исследована методом эквивалентной (гармонической) линеаризации. В статье автоколебания фрактального осциллятора исследуются методом численного интегрирования его уравнений движения.

1. Дифференциальная модель осциллятора

Физический прототип АФО подробно описан в статье [5]. Показано, что математически он определяется дифференциальным уравнением движения относительно нормированной осциллирующей переменной x ( t ), содержащим производную дробного порядка 0 < а < 1:

L 2 x ( t ) 7^ (0 ^a D ^а g ( x ( t ) ) .                         (1)

Здесь L ² _t – оператор квазигармонического осциллятора с собственной частотой to g и добротностью Q :

2 d ²

L t = d ? ⁺

^to 0 d

Q dt

+ ^to 0 ;

D ^а — оператор дифференцирования Капуто по-

рядка а:

d а о

¹-----[ ^{(.) т} d т ;

Г(1 -a) J ( t -т)^а

g ( x ) – нормированная передаточная функция активной нелинейности в цепи обратной связи; Г(.) — гамма-функция; у — параметр глубины обратной связи. Предполагается также, что АФО возбуждается из нулевого состояния через флуктуацию производной: x (0) = 0, у (0) = x '(0) = У 0 .

Отметим, что система (1) с кубической нелинейностью, например,

g ( x ) =

-

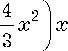
в пределе а ^1 переходит в классический осциллятор Ван дер Поля.

Предполагая в дальнейшем численное интегрирование уравнений движения, проведем в (1) нормировку времени путем перехода t ^ to 0 1 . Сохранив для временного аргумента прежнее обозначение, получим

L t x ( t ) = y D a g ( x ( t ) ) .                               (3)

Уравнение (3) примем за основу разностной модели АФО.

2. Разностная модель осциллятора

Определив сетку дискретного времени t n = n А, аппроксимируем дробную производную Капуто

конечными разностями:

da f (t )|   = n А

АаГ(2 - а)

У ( f ( к А) — f (( к — 1)А) ) х к = 1

х (n - к + 1)1-а - (n - к)1-а )+ O(А2).

Второму порядку погрешности в (3) соответствует аппроксимация дифференциального оператора L ² _t по методу Хойна (двухэтапному методу Рунге – Кутта; см., например, [6]). Введем обозначения x n = x ( n А), y n = x '( n А) для приближенных решений в момент времени t n = n А и

1 ⁿ

D n ( x ) = -;;-------- X ( g ( x [ к ]) - g ( x [ к - 1]) ) х

^П² -а) к =                    (5)

х (n - к + 1)1-а - (n - к)1-а)

для приближения дробной производной (4). В этих обозначениях разностный алгоритм интегрирования задачи Коши для дифференциального уравнения (3) имеет вид к1 x = yn,

к1 y = -xn - yn + YDn (x),

Q к2 x = yn + к1 yА, xn+1 = xn + "2" (к1 x + к2x ),                        (6)

к2 y = -(xn + к1 x А)-Т?(Уп + к1 У А)+У D“+1(x), Q yn+1 = yn + "2 (к1 y + к2 y ), n = 0,1,2,...; x о = 0, yo = a, Dga (x) = 0.

Явный алгоритм второго порядка точности (6) определяет разностную модель АФО.

• 3.    Результаты моделирования

Результаты моделирования процесса установления автоколебаний АФО по алгоритму (6) с шагом А = 0.15 иллюстрируют приведенные ниже рисунки.

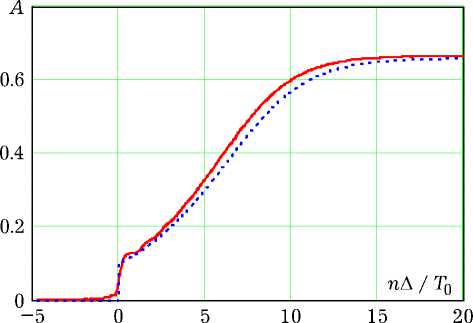
На рис. 1 сплошной линией представлен график изменения огибающей A ( n А) автоколебаний x ( n А) осциллятора с нелинейностью (2) и пара

метрами a = 0.5, Q = 10, у = 0.25. Временной аргумент нормирован на собственный период 7 0 = 2п контура в системе (3). Комплексная огибающая выделялась по методу аналитического сигнала с предварительной фильтрацией высших гармоник автоколебаний.

Пунктирной линией на рис. 1 показан график изменения огибающей, рассчитанный интегрированием первого из укороченных уравнений

dA A . Q-’(1 - A2 \in [ a — , — dt 2 । I 2 JJ (7) d ф dt 1 - 2Y (1 - A2) f n) зos a , I 2J полученных в [5] методом эквивалентной линеаризации (МЭЛ).

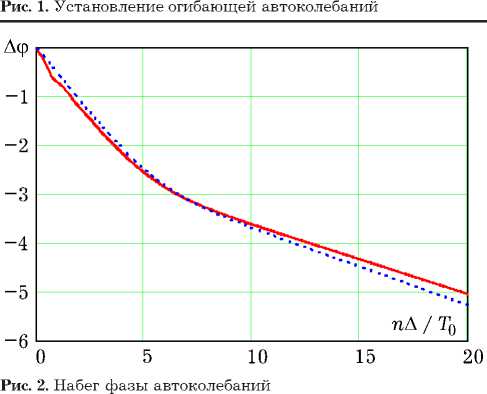
На рис. 2 пунктирной линией показан график набега фазы Аф( t ) = ф( t ) - ф(0) автоколебаний АФО, построенный по решению второго укороченного уравнения (7). График набега фазы автоколебаний x ( n А) в разностной модели АФО (6) изображен на рисунке непрерывной линией.

Из сопоставления представленных и аналогичных им численных и приближенных аналитических результатов следует, что МЭЛ при

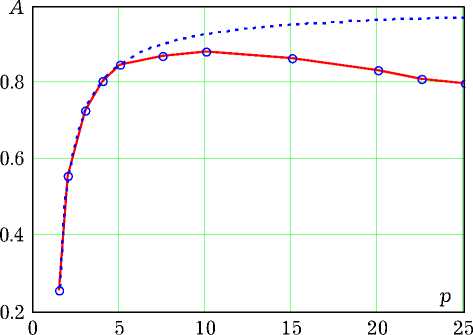
Рис. 3. Зависимость амплитуды автоколебаний от параметра возбуждения

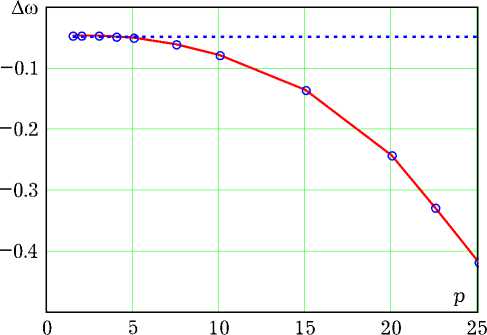
Рис. 4. Зависимость поправки на частоту автоколебаний от параметра возбуждения умеренных уровнях возбуждения (уQ < 5) вполне применим для анализа АФО в широком диапазоне их параметров: а > 0.25 и Q > 10.

В существенно нелинейном режиме возбуждения (уQ > 10) целесообразно использовать численную модель (6), т. к. МЭЛ в этом случае дает завышенные значения амплитуды. Этот факт отражает рис. 3, на котором приведены зависимости амплитуды установившихся автоколебаний от параметра возбуждения p = уQ для АФО с а = 0.5 и Q = 10. Пунктирная линия соответствует результатам МЭЛ, а непрерывная – результатам численного моделирования. В то время как зависимость A = A(p) в МЭЛ с ростом p выходит на насыщение, результаты численного моделирования демонстрируют некоторое уменьшение амплитуды первой гармоники, что объясняется перекачкой энергии в высшие гармоники автоколебаний – эффектом, учтенным в численной модели и не учтенным в МЭЛ. Известно [7], что обогащение спектра автоколебаний гармониками основной частоты приводит к понижению частоты генерации и возникновению у автоколебательной системы свойства неизохрон-ности. Указанное явление иллюстрирует рис. 4 с приведенными на нем графиками зависимости поправки на частоту Ato = ф'(t) установившихся автоколебаний, рассчитанными в приближении МЭЛ (пунктирная линия) и в рамках численной модели (6).

Заключение

Представленный здесь численный алгоритм расширяет возможности математического моделирования активных фрактальных осцилляторов и позволяет установить пределы применимости приближенных аналитических методов моделирования.