Численный анализ динамики криволинейного трубопровода

В результате различных внешних факторов (подвижки грунта, вибраций от техногенных процессов, сейсмической активности и других), а также собственной неустойчивости, трубопроводы отклоняются от своего проектного положения [1, 2]. Исследование процессов изменения трассы трубопроводов и разработка методов диагностики состояния их профиля является одной из актуальных проблем.

Данной тематике посвящено большое число монографий и обзорных статей. Влияние сейсмических явлений на трубопроводы подробно изложено в [2]. Задачи взаимодействия инженерных конструкций с жидкостью выделились в новое направление вычислительной и прикладной механики, получившее за рубежом название «Fluid-Structure Interaction Problems». Обзоры соответствующих публикаций сделаны в [3, 4]. В серии сборников [5] представлены вопросы морских технологий, связанные с конструированием и эксплуатацией подводных райзеров — трубопроводов, предназначенных для подъема из скважины полезного продукта, отвода использованного бурового раствора и тому подобное.

В цикле работ [6–11] выполнены исследования кинематики и динамики изогнутого трубопровода, построены математические модели, созданы алгоритмы для их численного анализа, решены тестовые примеры. В [7] проанализирована геометрия трубопровода и построена математическая модель для решения внутренней задачи распространения квазилинейных гидроупругих колебаний. В [8] проведена верификация этой математической модели на основе известных из литературы данных и установлено, что предложенная модель является более универсальной, чем существующие. В [9] рассмотрены нелинейные волны в прямых и изогнутых трубах; для анализа волн получены уравнения Кортевега–де Вриза и Клейна–Гордона–Фока; доказана достаточность уравнений для достижения необходимой точности математического моделирования.

В статьях [6, 10, 11] обсуждается внешняя задача медленного деформирования подземного трубопровода. Работа [10] посвящена анализу кинематики и обоснованию математической модели движения трубопровода во внешней среде. В [6] построенная математическая модель уточнена, создан и протестирован алгоритм для ее численной реализации. В [11] изучено движение трубопровода как растяжимого стержня в вязкой среде.

В [6–10] для редукции получившихся систем дифференциальных уравнений к одномерным по пространству уравнениям используется универсальная геометрия изогнутого трубопровода. Алгоритм редукции является общим для всех этих задач.

Целью данной работы является численный анализ математической модели трубопровода как геометрически нелинейной оболочки, содержащей поток жидкости и окруженной вязкой внешней средой. Решаются задачи: а) нахождения перемещений и деформаций протяженных трубопроводов при постоянном перепаде внутреннего давления в потоке жидкости; б) расчета динамики оболочки с продольным профилем в виде цепной линии, в которой перемещается быстрый поток жидкости; в) определения перемещений протяженного трубопровода при переменном перепаде внутреннего давления.

В численных экспериментах показано, что поперечные сечения протяженного тонкостенного криволинейного трубопровода испытывают депланацию, а деформации стенки трубы носят сильно неравномерный характер в больших окрестностях точек закрепления или экстремумов кривизны профиля. Установлено, что предложенная математическая модель описывает известный эффект «обратного поведения трубопровода» в случае профиля, имеющего вид цепной линии. Найдено, что исследуемая модель применима в случае динамически меняющегося внутреннего потока.

2.    Построение математической модели

Рассматривается металлическая труба длиной L с круглым поперечным сечением радиусом R0 и малой толщиной стенки h ; в недеформированном состоянии ее осевая линия — слабоизогнутая плоская кривая Г0 = {x0, у0 : x0 = x0(5), у0 = у0(5)}, где 5 — естественный параметр (длина дуги). Под действием постоянного перепада давления по трубе со скоростью 950 движется стационарный поток жидкости.

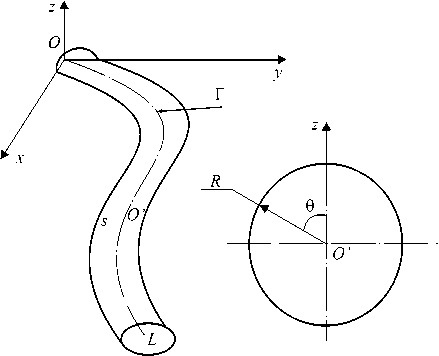
Рис. 1. Геометрия механической системы: { O , x , у , z } - глобальные декартовы координаты, { O , 5 , 0 , R } - криволинейные координаты

продольного профиля.

На основе алгоритма перехода от трехмерного

Ставится задача вычислить положение осевой линии Г = { x ( 5 , t ) , у ( 5 , t )} и деформации стенок трубопровода. Предполагается, что на больших интервалах времени внешняя среда ведет себя как сильно вязкая жидкость, а начальный радиус кривизны осевой линии р ₀ ( 5 ) велик по сравнению с радиусом трубы.

Системы координат (Рис. 1), используемые для математического моделирования движения трубопровода, описаны в [7, 10]. Криволинейные координаты { O , 5 , 0 , R } строятся на оси Г так, что 5 — длина дуги ( 00 ' ) , { O ', 0 , R } — полярные координаты в поперечном сечении трубы. В отличие от криволинейных координат в [12], используемые здесь координаты позволяют рассматривать более общую геометрию с переменной кривизной

упругого тела к оболочке, предложенного в [13],

построена математическая модель трубопровода как технической оболочки, погруженной в вязкую среду [10]. Для применимости этой модели необходимо выполнение условий В.З. Власова [13]:

h* = h/R ₀ <  0,1;    min ( L , р ₀ )/ R >  4.

Предполагается малым параметр:

X = R max |к₀ ( 5 )| « 1,                                         (2)

• к ₀ ( 5 ) — кривизна осевой линии Г ₀.

Согласно традиционному подходу [13], перемещения срединной поверхности трубы вдоль осей криволинейных координат 5 , 0 , R обозначаются как и , v , w , соответственно. После перехода к безразмерным переменным и неизвестным С = 5 /I, т = ю t , и ' = u/R ₀, v ' = v/R ₀, w' = w/R ₀, где I , ю — характерные масштабы длины и времени, безразмерные перемещения запишутся в виде:

и '(С, 0, т) = и0 (С) + Xи1 (С, T)sin 0 + O(X2), v '(С, 0, т) = X v,(C, T)cos 0 + O (X2),                                        (3)

w '(С, 0, т) = Wo(C) + х w^C, T)sin 0 + O (X2), u0,v0,w0, u1,v1,w1 — функции одной пространственной переменной. Возможность такого разложения обоснована в [7, 10]. Посредством (3) из уравнений устраняется независимая переменная 9, тем самым задача редуцируется к одномерной по координатам. Окончательная формулировка уравнений математической модели [6] выглядит следующим образом:

д2u„      дж    з Г дwn д2wn а2 —т- + va —- -а3 —-—з0

дZ ² дZ ( dZ dZ ²

-

- .PC, s0

E h 2

h *2 I 2 w „ +-- а

⁰ 12 I

^{д 2 ж} 0 dZ ²

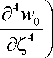
д u„

+ va —- дZ

-

a I д w ₀ I |"s^ ^J

-¹- [ P a + / Р9 20 ( L -Z ) -P gr gh 0 } E h                        ^J

2 д u. a —г

—

1 -v u 21

—

1 + v д v,      д w   . 1 -v

---a— + va + f ---u,

2 дZ дZ L 2

1 -v

—

„    д² u„      ,, _s д w,

2 a²—£+a (1 -v )—0- дZ          дZ

-

з Г д w д² w„ ■ a —¹— t

(дZ дZ

дч ^{д 2} w 1_{+ 3 a} 3 f ^{д w} 0 ^ w дZ дZ ^{2 J J} дZ дZ ²

p t R ₀ ² to ² д ² u 1 .

E*    дт ’

1 -v ₂ д ² v .           1                2 u * ц                 1 + v д u .

a v +a

2      дZ ^{2    1} E h R 0 ( 0,5 - In |yp gr X u_xR 0 /(4 ц )| )     2 дZ

^{+ w} 1 ^{+ f} l ^w 0

-

3 - v д u„ --a —-

-

дZ

a ²

д w ₀ д w 1 _p _tR 0 ² to ² д ² v 1 . дz дz = E* дт? ’

h I ₄ д w wi +-- a —-— a ^{w 1} 12 |    дZ ⁴

₂ д ² w )     д u.

-²—₂ +va —¹ -V1 + f дZ ² J     дZ ^v

д u„

^{2 v} w 0 + ^{(1 -v )} a-дZ^L

-

₂ д w , д w a —-—¹

дZ дZ

₊ a . Г ^{д w} 1

2 ⁷ ( дZ ^J

1 _p . 2 _f 2 u; цp tR^ д ² w , E*h* L ^{P f} s 0     R 0 ( 0,5 - In |yp gr X u * R 0 /( 4 ц )|) ]      E*    дт ^{2 .}

Для замыкания постановки задачи деформирования трубы-оболочки в вязкой среде в результате действия внутренних нагрузок система уравнений (4)–(8) дополняется краевыми и начальными условиями:

u0 = w0 = v = w = 0, ^0- = —- = 0 при Z = 0, Z = L' и любом т; 0     0    1     1 дZ дZ u. = v, = w = 0, ^u1 = ^1 = 1- = 0 при любом Z и т = 0.

¹¹¹ дт дт дт

₽ = 7Г;     Ф t (9 s 0 ) = R"₽920;

4 R ₀                  2

Re = ⁹ V o R ⁰ ;     v _f =ц _f /p _f ;

X 1 = I⁴ -

Re

0.221

^X 1 = ^0,0032 + ₁;¹<0лз7 ^,

Re ^,

Re < 2000;

Re > 2000.

Формулы для X 1 , р найдены И. Никурадзе и приведены в классическом труде Л.Г. Лойцянского [14], в котором изложена методика учета трения потока жидкости в шероховатых трубах.

Текущие координаты произвольной точки x , у , кривизна к и скорость поперечного движения u * осевой линии выражаются через искомые функции с помощью формул:

ГУ- х          ,    dx0     , Xa dy0 /, А x(Z,т) - x0(Z) + a777 uо + ”—"V7+v 1 + w 1), d Z x      zz-x dy 0      Xa dX 0 /\

y(^,т) - y0(Z) + a — u0 — ,  ,„ (v 1 + w 1), d Z

1 d2 y f dx V •- R оюГ д V1 dw 12 ^^( Z, т)                           , u                      1

/ d Z I d Z)      ¹     2 l дт дт J

Соотношения (4), (5) называются уравнениями в нулевом приближении, а (6)–(8) — уравнениями в первом приближении. В нулевом приближении трубопровод ведет себя как прямолинейный и цилиндрический, и точное решение краевой задачи (4), (5), (9) найдено в статье [6]. Его прямой подстановкой в (4), (5) проверяется утверждение, что на большом (по сравнению с R ₀ ) расстоянии от концов трубы перемещения можно аппроксимировать функциями:

w « [ P. + 1 09 20 ( L '-Z ) -P gr gh 0]/ ( E * h *) , u 0 « ^ 09 2c Z ( L '— Z )/ ( 4 E*h a) .

Начально–краевая задача первого приближения решена по явной трехслойной разностной схеме с уточнением значений, способ построения которой изложен в [15]. В предложенном здесь алгоритме v ₁ и w ₁ вычисляются по явной схеме, а для определения u ₁ употребляется неявная схема. Если ограничиться применением только явной разностной схемы, то не удастся добиться устойчивости ни при каком, даже сколь угодно малом шаге по времени. Этот эффект известен из теории разностных схем газовой динамики [15].

Расчетные формулы для v ₁ и w ₁ имеют вид:

v i

- 2 v j

—

v i

E у h !

P tR>" h Z

1 — V f J

1 V

2 ^{l +}

— 2 v j + * ] ■

E * h _т ²

P R v

v j

—

2 ц h 2                   u ,**                   E * h 2 J 1 + v a * j.     *

-+5(u,+1 — u,_,) + w + hR0Pt®  0,5 — ln|ypgrXu/R/(4ц)|  ptR0 to [ 4 hZ wi+1 - 2 wj — w* 1

va _Г j

+--1 u^J_t

2 h _Z ^{l 1 +}

—

+^

—

3 — v a / w0i      4   h" (u0(,+1) — u0(, —1)

E * h _т ²

p t R ₀ ² ® ²

. h *² w, +^TT

uh ) ^{— v j +} f i*

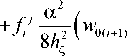
^— 4 h ⁽ w 0( i + 1) ^— w 0( i — 1) ⁾⁽ w * ^— * )

₁₂ h ⁷" ( w i+ 2 ^{— 4 wj} +1 ^{+ 6} w i ^{— 4} w j—1 ⁺ w i—2 )

^{2 v w} 0 i ^{+ (1 — v)}^ h “ ( ^u 0( i + 1) ^{— u} 0( i — 1) )

^{— w} 0( i — 1) )

E ’ h⁷

—

air * h ^{2 (} w^{i + h} Z

a ²

4 h _Z ^{2 (   0(} ‘ ^{+ 1)}

— 2 w j + w^ )

+

^{— w} 0( i — 1) )( w j+1 ^— w — 1 ) ⁺

P<9 2„ f * г^{2Ц UL}j

R 0 ( 0 , 5 — In |YP gr x u * * R 0/( 4 ц )| )

^;( * ^{+ 1)} - R ⁰ ^ f v ^{+ 1} — v * + w * ^{+ 1} — w 2   ( i - 2 ,

2 h _т ^l '          '        '           ' ^J               ,

N — 2).

После этих расчетов вычисляется u * ^{+ 1} по неявной схеме:

T7 * _ 2 u*+1 — -E-У- h 2 ■ (u^ 2u* + u*1 )+ _        т2 u* - 2ui ui 2  PtR0® 1 + E * h2 . 1 1 + v a f v*+1 hZ -    PtR >г PtR 2®2 I 4 h Z i u0i — 2T2"(u0(i+1) — 2u0i + u0(i—1)) + (1 — v) 7й”(w0(i+1) — w0(i—1)) z,            ru                                           Z-1U

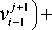
+^a ( w A¹— w *+ ) +^

2 h _Z^v              '

З а ³ jj

⁺ 2 h 3 f, ⁽ w 0⁽ _{Z +} 1 ₎

- ^w 0( i - 1) ) ( W o( _{i + r)} - 2 w _{O i} + w 0 , - 1) ) [;

u j ^{+ 1} = 0 ,      u ^{+ 1} = 0 (i = 1 , N - 1) .

В соотношениях (11), (12) обозначено: h _т и h , — шаги по времени и координате; N — количество узлов сетки по продольной координате; Z , = i ' h _z , u , * j = u* i ( Z , ,t j ), u ₀ , = u ₀( Z ), w _{0 i} = w ₀ ( Zj ), u ^j = u ₁ ( Z,T j ), v j = v ₁( Z , ,t j ), w j = w ₁( Z , ,t j ). Краевые условия учитываются стандартным образом [15]. Для правильного учета нелинейности на каждом шаге по времени выполняется пересчет кривизны по формулам (10). Количество шагов по времени ограничивалось условием достижения стационарного решения.

В заключение рассуждений, связанных с построением математической модели движения трубопровода с протекающим по нему потоком жидкости, следует обратиться к соотношениям (3). Отсюда следует, что физический смысл произведения ( X u ₁ R ) — это расстояние, на которое точка поперечного сечения выходит из его плоскости, то есть депланация [16]. Этот факт проверяется прямым вычислением при u ₁ = const. По-видимому, впервые отклонение от закона плоских сечений в цилиндрической трубе наблюдалось в опытах В.З. Власовым [17].

3.    Численный анализ математической модели

Для верификации используемого подхода и построенной математической модели решено несколько модельных задач, в которых рассматриваются различные геометрии продольного профиля трубопровода, условия внутреннего нагружения. Математической моделью во всех задачах является система уравнений (4)–(8) с начальными и краевыми условиями (9) и дополнительными соотношениями (10).

• 3.1.    Варианты физических и геометрических параметров трубопровода

• 3.2.    Деформации и перемещения протяженных трубопроводов

Рассмотрены три варианта продольного профиля трубопровода.

Задача 1. Профилю отвечает кубическая парабола: у = 10 - 8 x ( x - 6000 )( x - 12000 ) , 0 <  x <  12000. Значения основных геометрических параметров: L = 12500 м; min |р₀| ® 3951,5 м. Скорость внутреннего потока жидкости равняется 9 _{5 0} = 1 м/с, расчетный интервал времени — T end = 864000с или 10 суток.

Задача 2. Профиль описывает дробно-рациональная функция: у = 40 ( 1 - 0,001 x )/ ( 1 + 10 ^{- 6} x ² ) , - 6000 < x <  6000. Значения основных геометрических параметров: L = 12000 м; min|р ₀| ® 1194,5 м. Скорость внутреннего потока жидкости составляет 9 _{5 0} = 1м/с , расчетный интервал времени — T end = 691200с или восемь суток.

Задача 3. Профилю соответствует уравнение цепной линии: у = - 21901,4 + + 21901,4ch ( ( x + 21859,2)/21901,4 - 1 ) , 0 < x < 3000 . Значения основных геометрических параметров: L = 3009 м; min|р₀ 1 ® 17092,4 м. Скорость внутреннего потока жидкости 9 _{5 0} = 10 м/с, расчетный интервал времени T end = 86400с или 1 сутки. Дополнительные параметры данной задачи: h = 0,023 м; R ₀ = 0,23 м; ц f = 0,1 Па^с; р f = 998 кг/м³.

Прочие физические и геометрические параметры во всех задачах совпадают: р gr = 1700кг/м ³ ; ц = 10000 Па^с; р t = 7200 кг/м³; h = 0,005 м; E = 2,07 - 10 ¹¹ Па; v = 0,24; R = 0,3 м; ц f = 0,667 Па^с; р f = 850 кг/м³ и примерно соответствуют потоку легкой нефти в стальной трубе. Отличия, имеющиеся в Задаче 3, обусловлены ее спецификой и будут пояснены ниже.

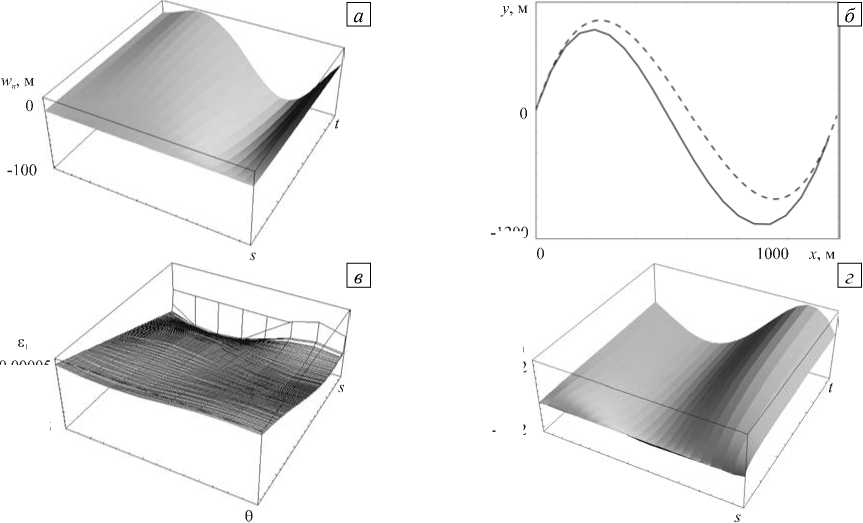
В результате численных экспериментов найдены функции перемещений осевой линии w n ( t , 5 ) , продольных и угловых деформаций стенки е ₁ ( 5 , 9 ) , ю ( 5 , 9 ) в конечный момент времени t = T end , координат осевой линии x ( t , s ), y ( t , s ). Для Задач 1, 2 вычислена также функция u ₁ ( t , s ), отражающая величину депланаций поперечных сечений. Во всех расчетах достигнуто стационарное состояние.

В Задачах 1, 2 моделируются относительно протяженные профили. На рисунке 2 изображены перемещения осевой линии, координаты профиля трубопровода, его продольные деформации и депланации, соответствующие условиям Задачи 1. Перемещения осевой линии (Рис. 2 а, б) иллюстрируют согласованность предложенной математической модели с фундаментальными законами механики: вычисленное с ее помощью результирующее перемещение профиля направлено в сторону равнодействующей распределенной по стенке трубы нагрузки, создаваемой текущим потоком жидкости. Продольная деформация стенки (Рис. 2 в), сильно изменяющаяся в большой окрестности точки закрепления, указывает на возможные депланации поперечных сечений трубы. Это предположение подтверждается графиком функции продольного перемещения стенки (Рис. 2, г), геометрический смысл которой и есть депланация сечения. Таким образом, численный эксперимент показал существование у протяженного тонкостенного криволинейного трубопровода депланации поперечного сечения величиной порядка 0, 02R0 .

-1200

-0,00005

-0,02

0,00005

Хи_х 0,02

а

Рис. 2. Перемещение осевой линии ( а ), координаты профиля в начале (пунктирная линия) и в конце (сплошная линия) расчета ( б ), продольные деформации стенки трубы ( в ), продольное перемещение в первом приближении ( г )

4xl0"6f

-4x10"

в

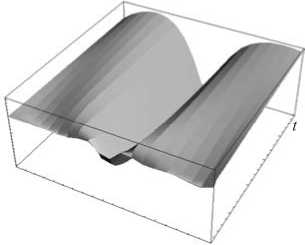
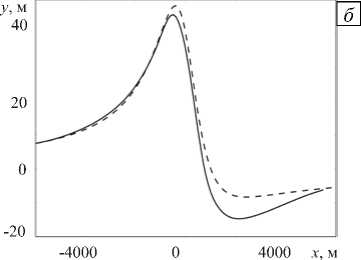
Рис. 3. Перемещение осевой линии ( а ), координаты продольного профиля в начале (пунктирная линия) и в конце (сплошная линия) расчета ( б ), угловые деформации стенки трубы ( в ), продольное перемещение в первом приближении ( г )

На рисунке 3 изображены координаты профиля трубопровода, его угловые деформации и депланации, полученные согласно условиям Задачи 2. Аналогично Задаче 1, изменение координат профиля в начале и конце расчета (Рис. 3, б ) указывает на соответствие используемой модели законам механики. Угловые деформации (Рис. 3, в ) иллюстрируют искажения поперечных сечений в большой окрестности точек изгиба и закрепления профиля. Также имеют место депланации поперечного сечения порядка 0,003 R ₀ .

• 3.3.    Деформации и перемещения трубопровода с профилем «цепная линия»

Свободно провисающая под действием силы тяжести нерастяжимая нить принимает форму, описываемую уравнением цепной линии. Приближенно можно полагать, что именно такую форму имеет осевая линия морского трубопровода–райзера [18]. Целью, которая преследуется решением Задачи 3, является анализ взаимодействия протяженной трубы с быстрым внутренним потоком и сравнение с результатами из [18], где найдены условия существования «обратного поведения райзера» — условия, при которых профиль трубопровода движется в сторону, противоположную направлению его прогиба.

В [18] главной характеристикой растяжимости трубы является параметр Ирвина, применяемый в механике кабелей: E irv = F/N a ^ ES t / N a , где F — внешняя распределенная вдоль трубы растягивающая сила; N a — внутренняя сила натяжения, N_a = ES_t s 1 ; E — модуль Юнга материала трубы; S t — площадь поперечного сечения ее стенки. В данной задаче единственной растягивающей силой является сила увлечения стенки трубы вследствие трения внутренним потоком жидкости, поэтому F = S_tb -Ф _t ( 9 _$ 0 ) , S b — площадь внутренней поверхности трубы, S b = 2 п (R - h / 2) L . Прямое вычисление дает E_irv ® 37,6. Это значение достаточно далеко от E_irv = 286 из [18], при котором явление «обратного поведения» не наблюдается.

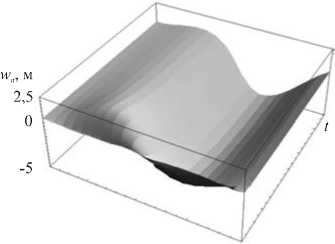
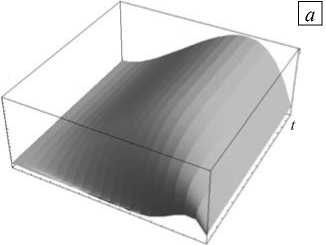
Результаты численного решения Задачи 3 изображены на рисунке 4. Показаны график нормальных перемещений осевой линии и координаты осевой линии для нескольких моментов времени. На рисунке 4, б видно, что труба смещается в направлении, противоположном первоначальному прогибу, что иллюстрирует явление «обратного поведения». Таким образом, результаты расчета по исследуемой модели согласуются с известными данными.

а

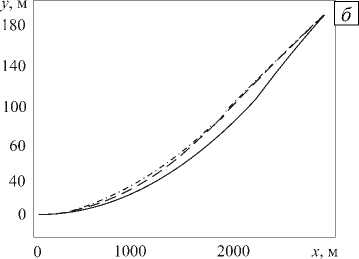
Рис. 4. Нормальные перемещения осевой линии ( а ) и ее координаты в разные моменты времени t ( б ): 10 минут (сплошная линия); 1 час (пунктирная линия); 24 часа (штрих-пунктирная линия)

• 3.4.    Перемещения трубопровода под действием динамического перепада давления

В Задачах 1–3 перепад давления на концах трубы считается постоянным, обеспечивающим стабильную скорость внутреннего потока жидкости. Для всех задач были поставлены численные эксперименты, в которых перепад давления менялся по кусочно-линейному закону:

	A Р 0 ,		t ^ t 0 ,
	A Р 0	k , — 1 k p + A ( t t 0	-A t )	, t 0 <  t <  1 0 + A t ,
A р =	k, A	Р 0 , Г k„ - 1/      x"		1 0 + A t ^ t ^ t 1 - A t ,
	A Р 0	1 +-— ( t l - t ) A t v 1    7 J	,	t 1 - A t <  t <  t 1 ,
	A Р 0			t >  t 1 .

Здесь Aр0 — перепад давления, обеспечивающий скорость потока 9$0; 10, t1 — время начала и конца скачка давления, соответственно; At — время, в течение которого меняется давление; кр — коэффициент повышения давления. Начальный перепад давления определяется из закона сопротивления для трубы [14]: Ap0 =X1 (L4R0 )pf920, остальные параметры задаются при постановке численного эксперимента. В примере, приведенном здесь Tend = 1209600с или 14 суток; kp = 1,5; 10 = 86400 с, t1 = 360000 с или 4 суток; At = 2 часа. Прочие параметры соответствуют Задаче 2.

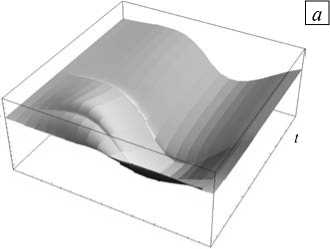
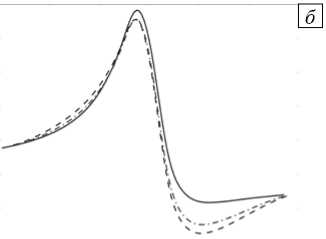
Результаты расчета перемещений содержит рисунок 5, а , где изображен участок 3D-графика перемещений, охватывающий интервал времени 125 часов с выделенной черным цветом той его части, на протяжении которой явно видно влияние скачка давления, приводящего к увеличению прогиба. Затем, по мере уменьшения давления, труба возвращается в положение, соответствующее положению окончательного равновесия при условиях Задачи 2. Координаты осевой линии в начале расчета, в момент времени, соответствующий наибольшему отклонению профиля, и в конечный момент времени показаны на рисунке 5, б . Установлено, что медленно меняющийся перепад давления в итоге приводит к такому же стационарному состоянию, как и постоянный перепад давления, но при условии, что конечные значения этих перепадов на трубопроводе будут равны между собой.

а

Рис. 5. Нормальные перемещения осевой линии ( а ) и ее координаты в разные моменты времени t ( б ): 10 минут (сплошная линия); 4 суток (пунктирная линия); 14 суток (штрих-пунктирная линия)

у, м

о

-10

-4000          0           4000 Л", м

Аналогичные результаты получены не только для трех рассмотренных здесь задач, но и для некоторых других [6], где адекватность математической модели нашла дополнительное подтверждение.

4.    Заключение

Результаты решения модельных задач доказали наличие депланаций поперечного сечения трубы при условиях перехода от трехмерного упругого тела к оболочке (условиях В.З. Власова). Установлено, что используемая математическая модель описывает явление «обратного поведения трубопровода» в случае профиля в виде цепной линии. Показано, что математическая модель сохраняет свою применимость в случае как медленного, так и динамического изменения внутреннего давления в заполняющем трубопровод потоке жидкости. Вычислены угловые и продольные деформации стенки трубопровода при достижении им состояния равновесия. Обнаружено, что неравномерность деформаций имеет место в больших окрестностях точек закрепления или экстремумов кривизны профиля.

Автор благодарен академику В.П. Мясникову за постановку задачи медленного деформирования подземного трубопровода и чл.-корр. РАН А.А. Буренину за постановку задачи движения трубопровода при динамическом перепаде давления, а также выражает признательность д.ф.-м.н. В.А. Рукавишникову за обсуждение текста статьи и поддержку.

Работа выполнена при финансовой поддержке РФФИ   (проекты   № 10-01-00060,

№ 11-01-98502-р_Восток_а) и Президиума ДВО РАН (интеграционный проект 12-I-П18-01).