Численный анализ композитной фермы

Одна из тенденции архитектуры 1990–2024 гг. [1]-[4] является пространство в зданиях и сооружениях, свободных от опор, перекрытое большепролетной конструкцией. Популярные конструкции покрытия – это металлические фермы совместно с профилированным настилом или сборными ребристыми плитами. В Российской Федерации мало уделяется внимания композитным (сталежелезобетонным) фермам. Одним из часто применяемых сечений в строительстве является металлическая ферма, на которую опирается железобетонная плита по профилированному листу. Совместная работа верхнего пояса фермы и железобетонной плиты обеспечивается с помощью гибких упоров.

Исследование композитных ферм актуально [5]-[6] тем, что конструкция имеет множество преимуществ. Например, бетон в плите эффективно работает на сжатие и обладает высокой огнестойкостью. Сталь в металлической ферме эффективно работает на растяжение. Арматура эффективно работает на сжатие и растяжение и способен компенсировать прочность в растянутой зоне бетона. Так же к преимуществам композитных ферм можно отнести высокую жесткость благодаря решетчатой структуре, которая состоит из поясов, раскосов и стоек.

Исследованием поведения трубчатой композитной фермы моста в области отрицательного момента занимались: Бейчен Пу, Сюйхун Чжоу, Юнцзянь Лю, Бинь Лю, Лэй Цзян. Описан новый тип композитной фермы, выполнен физический эксперимент и численные исследования прочности композитной фермы. Описано напряженно-деформированное состояние элементов композитной фермы. Определена область применение композитной фермы нового типа [7].

Исследованием совместной работы металлической фермы и железобетонной плиты занимались: Мачачек Йозеф, Чарват Мартин. Выполнены численные исследования при возрастающем уровне нагрузки сдвиговых усилий, изучены температурные эффекты и ползучесть Mirsayapov l.; Pavlov M.

Numerical analysis of composite truss;

бетона. Исследованы напряжения узлов соединений в области верхнего пояса фермы и влияние этих напряжений на железобетонную плиту [8]-[9].

Исследованием прочности в зоне действия изгибающего момента композитных стропильных ферм занимались: Лишэн Ло, Сяофэн Чжан. Выполнен физический эксперимент, численные и аналитические исследования несущей способности. Представлены графики зависимостей прочность-изгиб. Предложен метод расчета, основанный на степени сдвиговых усилий между металлической стропильной фермой и железобетонной плитой [10].

Исследованием соединений в композитных мостовых ферменных конструкций занимались: Го-ань Инь, Фа-синь Динь, Хаи-бо Ван, Ю Бай, Сюэ-мэй Лю. Выполнен физический эксперимент и численные исследования прочности соединений металлических раскосов в тело бетона. Представлены графики зависимостей нагрузка-напряжения. Описан характер разрушения исследуемых соединений. Представлены рекомендации по проектированию соединений исследуемого типа [11].

Исследованием соединений в композитной ферме занимались: Адбельхамид Бушаир, Ян Бужнак, Патриция Дюратна. Выполнены численные исследования влияний параметров диаметра материала, расположения соединительных элементов. Представлены графики зависимостей перемещения-усилия [12].

Исследованием прочности композитных ферменных балок занимались: Ян Буйнак, Петер Михалек, Веслав Баран, Збигнев Перковский. Выполнен физический эксперимент и численные исследования прочности балок и элементов, обеспечивающие совместную работу металлической фермы и железобетонной плиты. Представлены графики зависимостей прочность-перемещения. Представлены рекомендации по проектированию композитных ферм [13]-[16].

Исследованием напряженно-деформированного состояния композитной фермы занимались: Джоэл Мартинс, Синевал Перьера Младший, Эллен Ксавьер, Луис Нейва, Арлин Сарманьо. Выполнен физический эксперимент и численные исследования прочности композитной фермы. Описан характер разрушение композитной фермы. Представлены график зависимости напряжений-деформаций [17].

Исследованием напряженно-деформированного состояния композитной фермы занимались: Аугусто О. Б. Сильва, Ньютон О. П. Жуниор, Жуан А. В. Рекена. Выполнены численные исследования, предложен ручной метод расчета композитной фермы [18]-[19].

Анализ научных публикаций показывает, что одна из проблем композитных ферм – это обеспечение совместной работы металлической фермы и железобетонной плиты. В большинстве случаев совместную работу обеспечивают гибкие упоры. В практике проектирование по конструктивным требованиям невозможно расположить достаточное количество гибких упоров для обеспечения полной совместной работы металлической фермы и железобетонной плиты.

Авторы предлагают рассмотреть сечение, в котором верхний пояс из сварного таврового элемента заделывается на уровне верхнего армирования в железобетонную плиту. Совместная работа обеспечивается трением между сталью и бетоном, то есть адгезии материалов. В таком случаи железобетонная плита раскрепляет верхний пояс металлической фермы и усиливает сопротивление сжимающим усилиям. Элементы раскосов и стоек соединяются к верхнему поясу фермы через косынки путем сваривания элементов. Аналогично соединяется нижний пояс к раскосам и стойкам. Нижний пояс, раскосы выполнены из равнополочного уголкового сечения. Данное решение позволяет отказаться от гибких упоров для обеспечения совместной работы и горизонтальных связей для раскрепления верхнего пояса фермы, что приводит к экономии на материале и строительно-монтажных работах.

Таким образом, цель авторов заключается в исследовании напряженно-деформированного состояния композитной фермы численным методом. Выполнить анализ и определить элементы и участки разрушения с учетом физической нелинейности деформирования бетона, металлической фермы и арматуры. Определить несущую способность композитной фермы. Сравнить несущую способность с металлической фермой, где в качестве настила используется профилированные листы или сборные железобетонные плиты.

• 2    Materials and Methods

В качестве исходных данных для исследования принято сечение на (рис. 1) металлическая ферма из стали С345 геометрические характеристики представлены в (табл. 1). Железобетонная плита толщиной 200 мм из класса бетона В25, армированная сеткой диаметром 12 мм класс А500С. Общая высота сечение 1900 мм.

________________________________________ 1000 ________________________________________

^50,      250         100       200       100         250 J

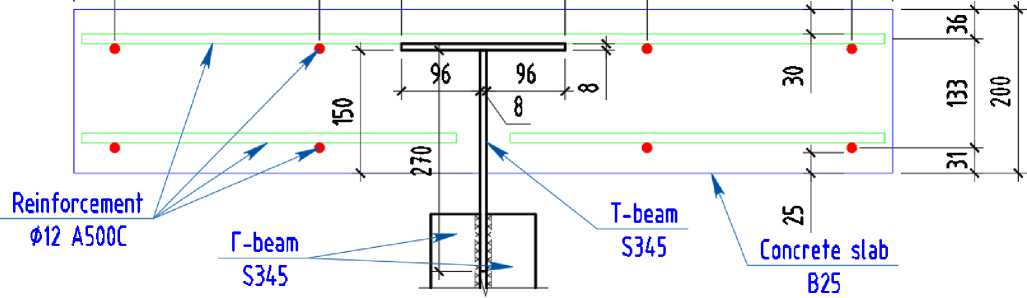
Рис. 1 – Исследуемое сечение фрагмент верхнего пояса

Fig. 1 – The section under study is a fragment of the upper belt

Таблица. 1 – Принятые сечения металлической фермы

Table. 1 – Accepted sections of the metal truss

Элементы фермы	Сечение, мм	Площадь сечения А, см2
Верхний пояс	Тавр 200х160х8	28.8
Нижний пояс	Парный уголок равнополочный 80х5	8.63х2=17.26
Опорные раскосы	Парный уголок равнополочный 80х5	8.63х2=17.26
Раскосы	Парный уголок равнополочный 60х6	6.92х2=13.84
Стойки	Парный уголок равнополочный 50х5	4.8х2=9.6

Расчетная схема (рис. 2) представляет собой ферму, опертую на две опоры шарнирно. Нагрузка приложена на железобетонную плиту равномерно по всей длине.

the axis of symmetry

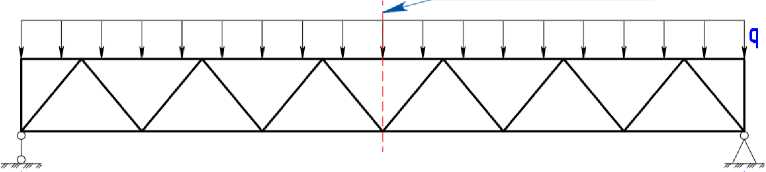
Рис. 2 – Расчетная схема фермы

Fig. 2 – The design scheme of the truss

3000x6=18000

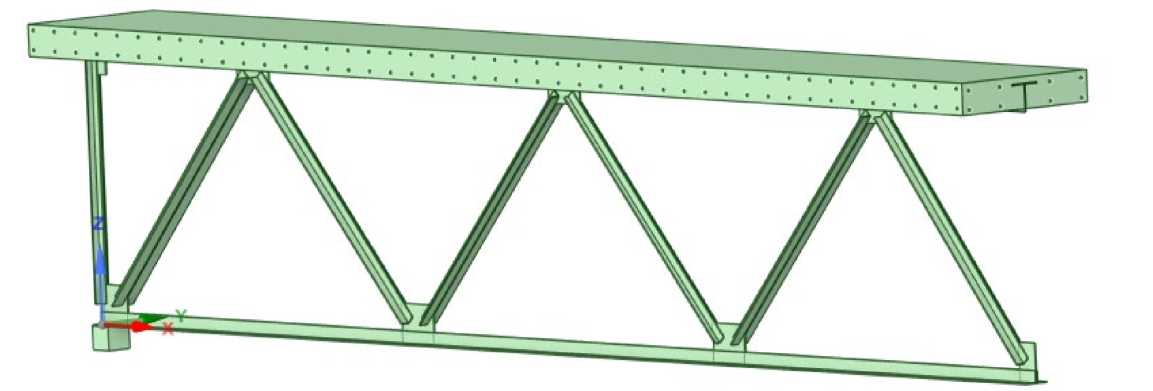
Рис. 3 – Расчетная модель в SpaceClaim

Fig. 3 – Calculation model in SpaceClaim

Характеристики материалов приняты нелинейными.

Для бетона принята диаграмма работы в соответствии с диаграммой деформации бетона на сжатие и растяжение предложенная академиком Н.И. Карпенко [20] (рис. 4). В ПК Ansys [ansys.com] задана теория прочности и пластичности Menetrey-Willam модель разупрочнения бетона HSD 6 (Hardening-Softening and Dilatation). Задана нормативные значения класс бетона В25 (рис. 5).

Для стали принята кусочно-линейная диаграмма в соответствии с приложением В1. Свод правил стальные конструкции 16.13330.2017 [21] (рис. 6). Заданы нормативные значения стали С345 (рис. 7).

Для арматуры принята двухлинейная диаграмма в соответствии с пунктом 6.2.14. Свод правил бетонные и железобетонные конструкции 63.13330.2018 [22] (рис. 8). Заданы нормативные значения класс арматуры А500С (рис. 9).

Для тумбочек, которые имитируют опоры, задана линейная работа стали.

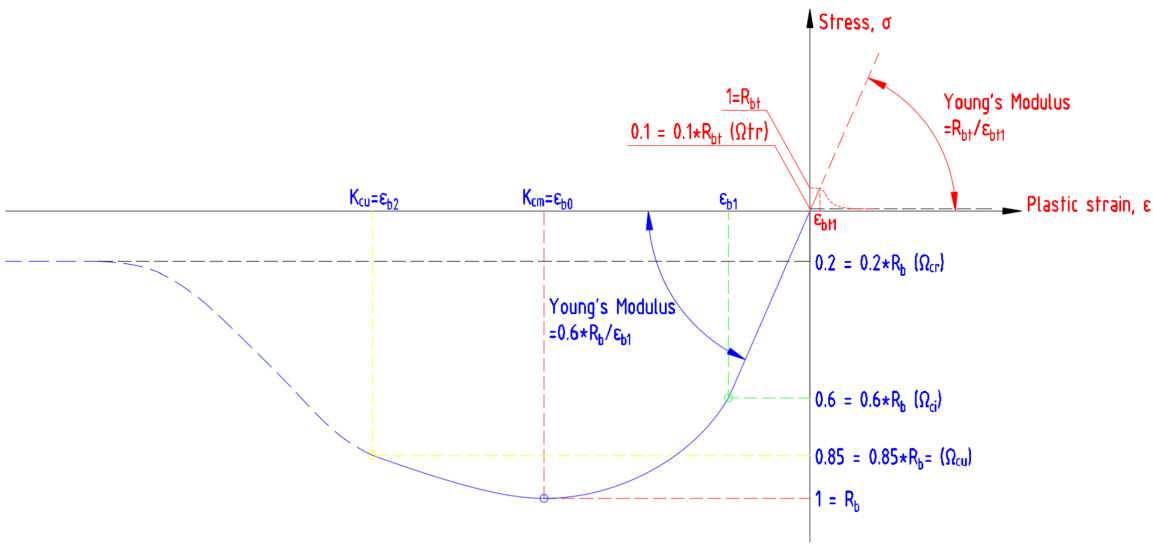
Рис. 4 – Экспоненциальная диаграмма работа бетона, адаптированная к теории Менетри-Виллама

Fig. 4 – Exponential diagram of concrete performance, adapted to the Menetrey-Willam theory

Properties of Outline Row 4: B25_V3

	A	В	C	D	E
1	Property	Value	Unit	*	ip)
2	Й Material Field Variables	Table
3	Й Density	2400	kg тл-3                       ^	□	□
4	0        Isotropic Elasticity			□
5	Derive from	Young's Modulus and Poisson's Ratio        _2
6	Young's Modulus	30000	MPa                  2		□
7	Poisson's Ratio	0,2			□
8	Bulk Modulus	l,6667E+10	Pa		□
9	Shear Modulus	l,25E+10	Pa		□
10	0 ^ Menetrey-Willam			□
11	В       Menetrey-Willam Base
12	Uniaxial Compressive Strength	18,5	MPa                  2		□
13	Uniaxial Tensile Strength	1.55	MPa                        _L		□
14	Biaxial Compressive Strength	22,2	MPa                  X		□
15	Й Dilatancy Angle	13	degree                          _▼		□
16	В Й Softening			□
17	Active Table	Exponential                              2.
18	Plastic Strain at Uniaxial Compressive Strength	0,0015008			□
19	Plastic Strain at Transition from Power Law to Exponential Softening	0,0028 584			□
20	Relative Stress at Start of Nonlinear Hardening	0,6			□
21	Residual Relative Stress at Transition from Power Law to Exponential Softening	0,85			□
22	Residual Compressive Relative Stress	0,2			□
23	Mode 1 Area Specific Fracture Energy	155,55	N тл-1		□
24	Residual Tensile Relative Stress	0,1			□

Рис. 5 – Характеристики бетона, заданные в ПК Ansys

Fig. 5 – Concrete characteristics, specified in the PC Ansys

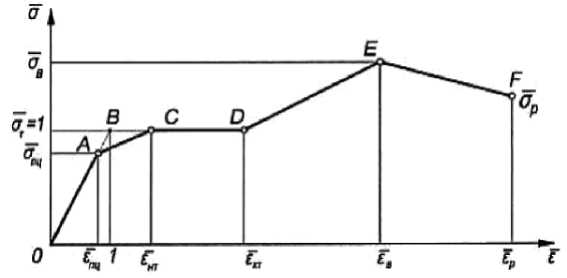
Рис. 6 – Кусочно-линейная диаграмма работы стали

Fig. 6 – Piecewise linear diagram of steelwork

Properties of Outline Row 5: S345

	A	В	C	D	E
1	Property	Value	Unit
2	^ Material Field Variables	Table
3	Й Density	7850	kg тл-3                                  _▼	□	□
4	0 *j^] Isotropic Elasticity
5	Derive from	Young's Modulus and Poisson's Ratio                        ’
6	Young's Modulus	2E+O5	MPa                                  _X		□
7	Poisson's Ratio	0,3			□
8	Bulk Modulus	1,6667E+11	Pa		□
9	Shear Modulus	7,6923E+10	Pa		□
10	В Й Multilinear Isotropic Hardening	Tabular		□
11	Scale	1			□
12	Offset	0	MPa		□

Chart of Properties Row 10: Multilinear Isotropic Hardening

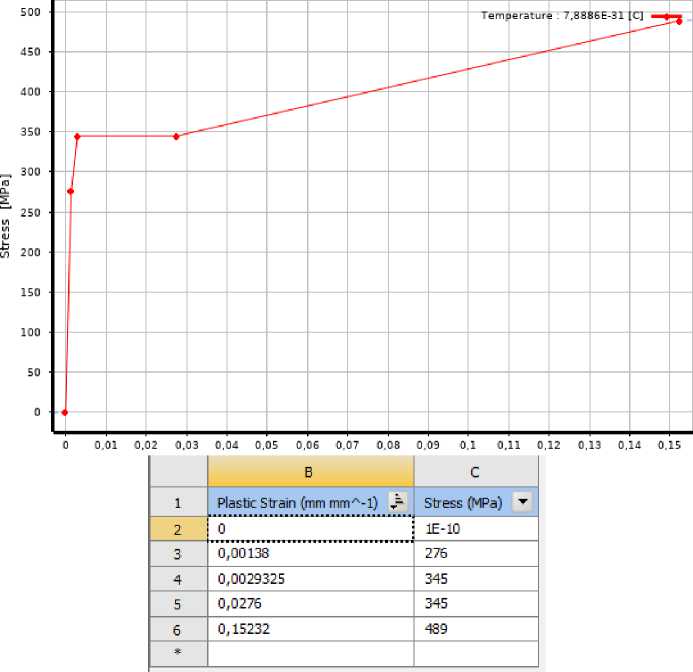
Рис. 7 – Характеристики стали, заданные в ПК Ansys

Рис. 7 – Steel characteristics specified in the PC Ansys

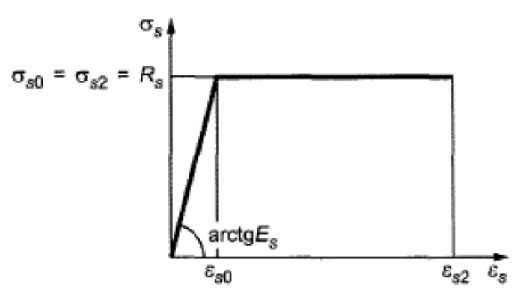
Рис. 8 – Двухлинейная диаграмма работы арматуры

Fig. 8 – Two-line diagram of the reinforcement

Properties of Outline Row 3: A500C

	A	В	c	D	E
1	Property	Value	Unit	•J	$3
2	Material Field Variables	В Table
3	Й Density	7850	kg тл-3                                  _▼	□	□
4	□        Isotropic Elasticity
5	Derive from	Young's Modulus and Poisson's Ratio                         T
6	Young's Modulus	2E+O5	MPa                                  _L		□
7	Poisson's Ratio	0,3			□
8	Bulk Modulus	1,6667E+11	Pa		□
9	Shear Modulus	7,6923E+10	Pa		□
10	□        Multilinear Isotropic Hardening	В Tabular		□
11	Scale	1			□
12	Offset	0	MPa		□

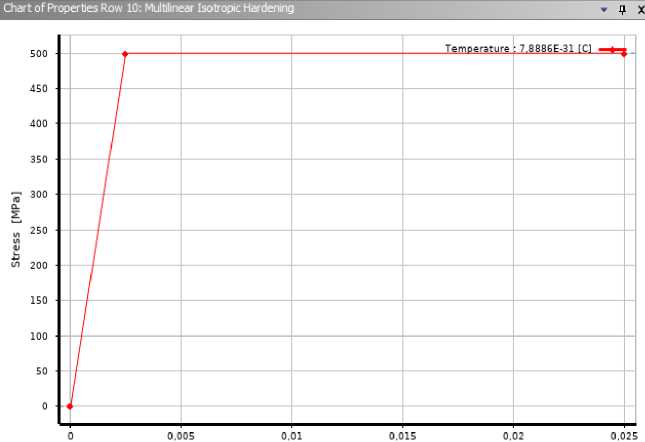
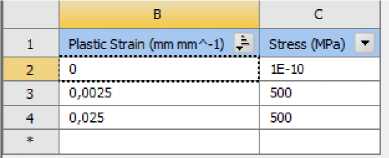
Рис. 9 – Характеристики арматуры, заданные в ПК Ansys

Fig. 9 – Reinforcement characteristics specified in the PC Ansys

Приняты следующие контакты между элементами сечения: 1) между тумбочкой и нижним поясом фермы значение «Frictional» с коэффициентом 0.5 [23] для имитации шарнирной опоры; 2) между железобетонной плитой и частью верхнего пояса фермы, которая заделана в плиту значение «bonded» то есть трение между элементами отсутствует за счет обжатия и адгезионных свойств материалов; 3) между стальными элементами значение «bonded».

Приняты следующие граничные условия: 1) на нижнюю поверхность опор задана «Fixed Support» моделирует жесткую заделку; 2) на боковые грани железобетонной плиты поперек фермы задан «Displacement» которая ограничивает перемещение по Y.

На первом шаге задается загружение от собственного веса конструкции значение «Standard Earth Gravity». На втором шаге задается равномерно распределенная нагрузка по всей поверхности железобетонной плиты значение «Force» с силой по 225000 N.

Для моделирования симметрии задано значение «Symmetry region» на торец сечения по оси симметрии (рис. 2).

Для анализа результатов необходимо вывести следующие данные: 1) Normal Stress (нормальные напряжения); 2) Stress Equivalent (von-Mises) (эквивалентные напряжения); 3) Equivalent Total Strain (относительные деформации); 4) Total Deformation (полные деформации); 5) Shear Stress (касательные напряжения); 6) Force Reaction (опорная реакция) [24].

• 3    Results and Discussion

  Отказ сечение зафиксирован на 0.95 секунде после начала испытания численной модели. Несущая способность составила P_ult = (225000 ∙ 2) ∙ 0.95 = 427500 N = 43.6 т . Общие деформации (рис. 10) вертикальные перемещение в момент отказа сечения составляет 93.1 мм.

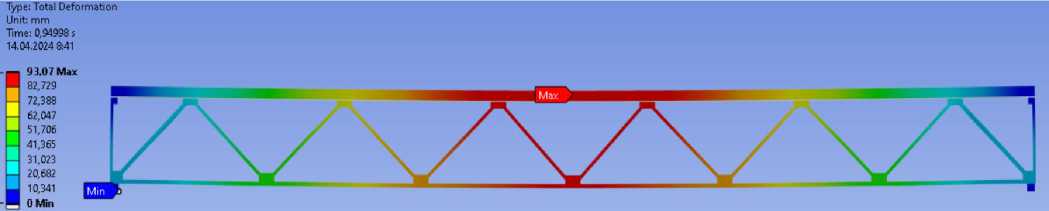
Рис. 10 – Прогиб композитной фермы

Fig. 10 – Deflection of the composite truss

Рассмотрим участок действия нормальных напряжений посередине пролета.

Нормальные напряжения в железобетонной плите (рис. 11). В сжатой зоне 13.45 МПа, что не превышает сопротивление бетона на сжатие Rb,n=18.5 МПа. В растянутой зоне 1.534 МПа, что не превышает сопротивление бетона на растяжение Rbt,n=1.55 МПа.

Относительные деформации в железобетонной плите (рис. 12). В сжатой зоне 0.00041 мм/мм, что не превышает максимально допустимые относительные деформации £ _Ь2 = 0.0035 мм/мм. В растянутой зоне 0.000187 мм/мм, что превышает максимально допустимые относительные деформации £ _bt2 = 0.00015 мм/мм.

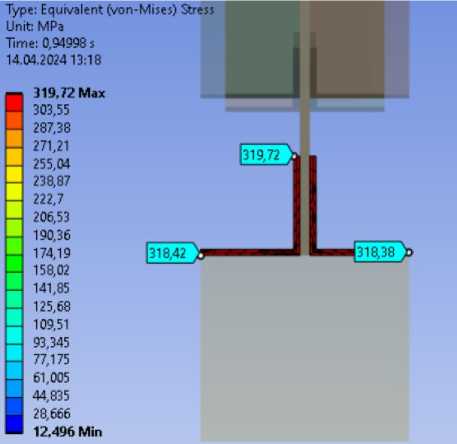
Эквивалентные напряжения по фон Мизесу (рис. 13). В растянутой зоне 319.72 МПа, что не превышает значение сопротивление стали для упругой работы R y =345 МПа. В сжатой зоне 63.63 МПа, в косынке 108.7 МПа.

Относительные деформации (рис. 14) В растянутой зоне составляют 0.00396 мм/мм, что превышает значение упругой работы стали 0.00138 мм/мм, в косынке 0.0011 мм/мм.

На основании полученных результатов можно представить расчетную модель следующим образом (рис .15). Пренебрежем вклад арматуры в несущую способность сечения.

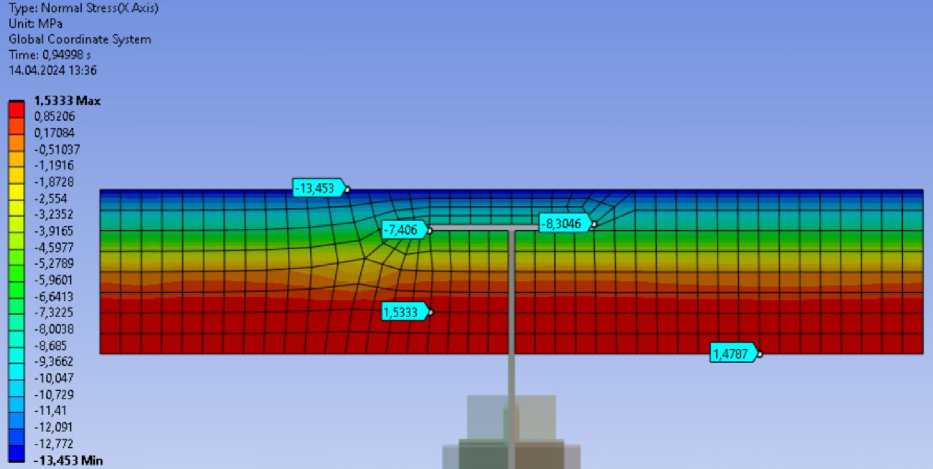
Рис. 11 – Нормальные напряжения

Fig. 11 – Normal stress

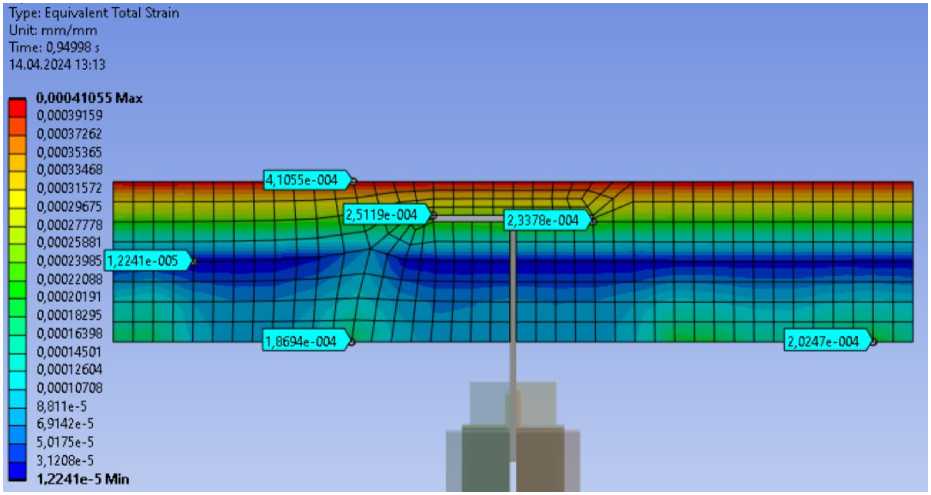
Рис. 12 – Относительные деформации

Fig. 12 – Equivalent strain

Type: Equivalent (von-Mises) Stress

Unit: MPa

Time: 0.94999 i

14.04.2024 16:45

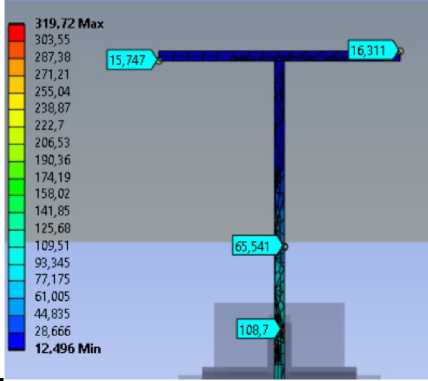
Рис. 13 – Эквивалентные напряжения (a – верхний пояс, b – нижний пояс)

Fig. 13 – Stress Equivalent (a – upper belt, b – lower belt)

a.

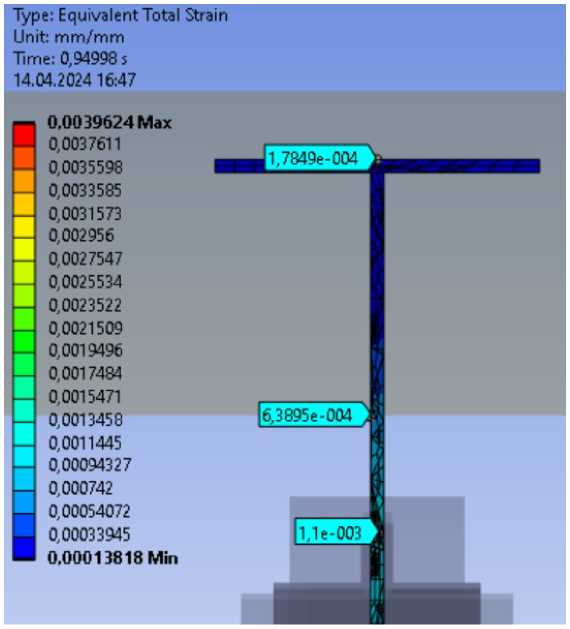
Рис. 14 – Относительные деформации (a – верхний пояс, b – нижний пояс)

Fig. 14 – Equivalent strain (a – upper belt, b – lower belt)

b.

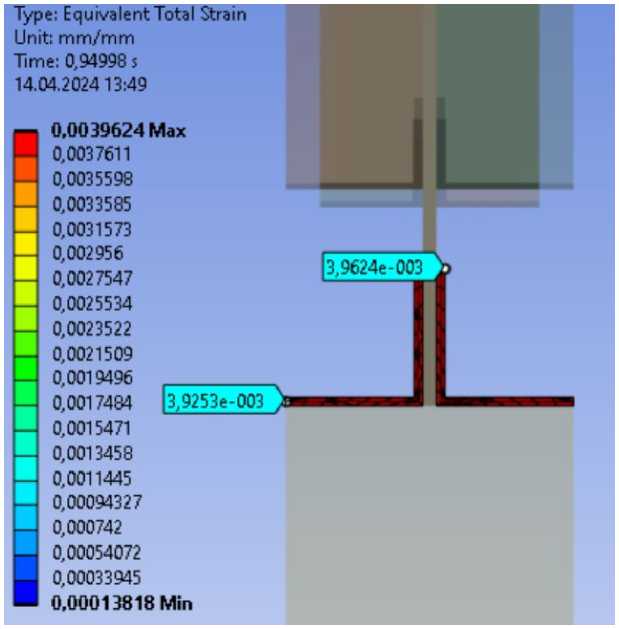
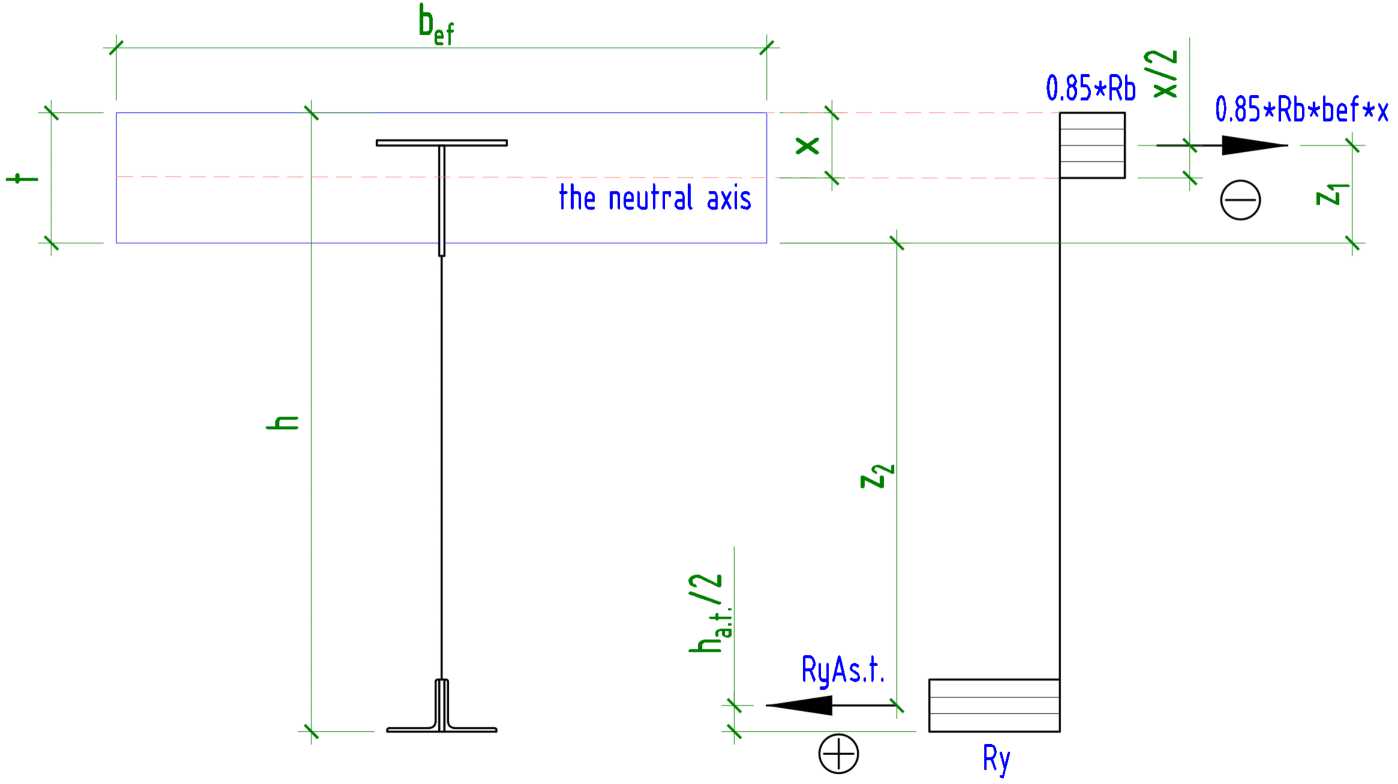
Рис. 15 – Расчетная схема для определения изгибающего момента

Fig. 15 – Calculation scheme for determining the bending moment

Выражение для определения предельного изгибающего момента будет иметь следующий вид:

xh

M = 0.85 • R, • b • x • ( t —) + R • A . • ( h — t —^^) ult                 b ef              2 y     s . t .                  2

Рассмотрим участок на расстоянии 1500 мм от опоры.

Нормальные напряжения в железобетонной плите (рис. 16). В сжатой зоне 5.43 МПа, что не превышает сопротивление бетона на сжатие Rb,n=18.5 МПа. В растянутой зоне 1.08 МПа, что не превышает сопротивление бетона на растяжение Rbt,n=1.55 МПа.

Относительные деформации в железобетонной плите (рис. 17). В сжатой зоне 0.003 мм/мм, что не превышает максимально допустимые относительные деформации £ _Ь2 = 0.0035 мм/мм. В растянутой зоне 0.000032 мм/мм, что не превышает максимально допустимые относительные деформации £ _bt2 = 0.00015 мм/мм.

Эквивалентные напряжения по фон Мизесу (рис. 18). В растянутой зоне 55.06 МПа, что не превышает значение сопротивление стали для упругой работы R y =345 МПа. В сжатой зоне (включая косынку) 341.05 МПа.

Относительные деформации (рис. 19). В растянутой зоне составляют 0.000552 мм/мм, что не превышает значение упругой работы стали 0.00138 мм/мм. В сжатой зоне (включая косынку) 0.004586 мм/мм, что превышает значение упругой работы стали 0.00138 мм/мм.

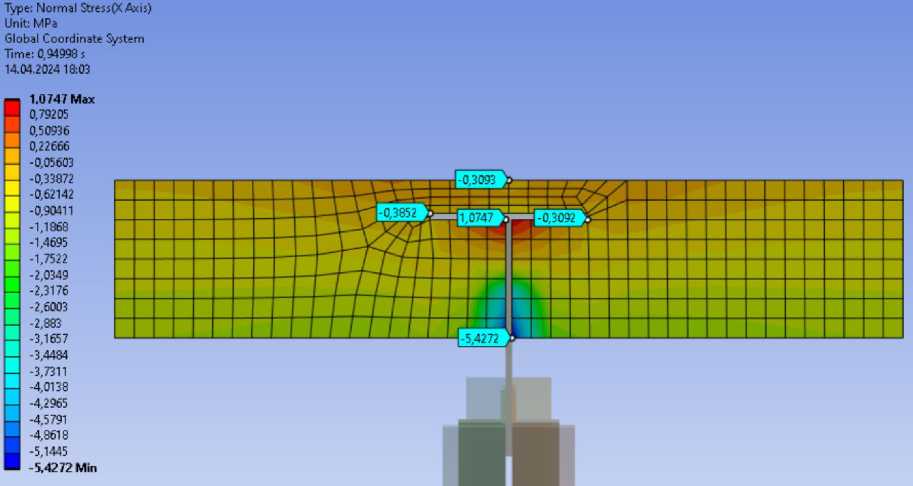
Рис. 16 – Нормальные напряжения

Fig. 16 – Normal stress

Type: Equivalent Total Strain

Unit: mm/mm

Tme: 0,94998 s

14.04.2 02418:05

0,0030976 Max

0,002 8776 0,0027476 0,0026176 0,0024876 0,0023576 0,0022276 0,002 0976 0,0019676 0,0018376 0,0017076 0,0015776 0,0014476 0,0013176 0,0011876 0,0010576 0,00092765 0,00079765 0,00066766 0,00053766 0,00040767 0,0002 7767 0,00014768

1J68e-5Min

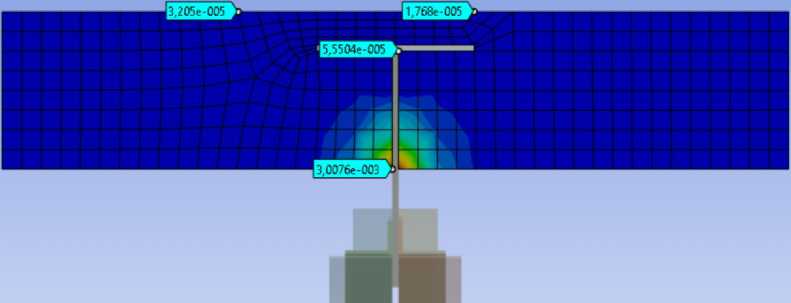
Рис. 17 – Относительные деформации

Fig. 17 – Equivalent strain a.

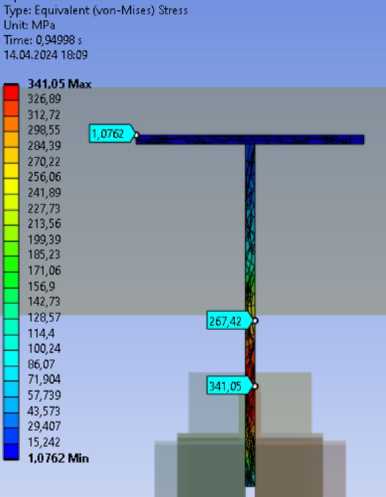
Рис. 18 – Эквивалентные напряжения (a – верхний пояс, b – нижний пояс)

Fig. 18 – Equivalent strain (a – upper belt, b – lower belt)

b.

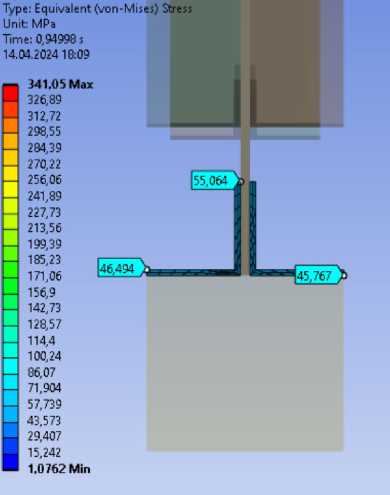
a.

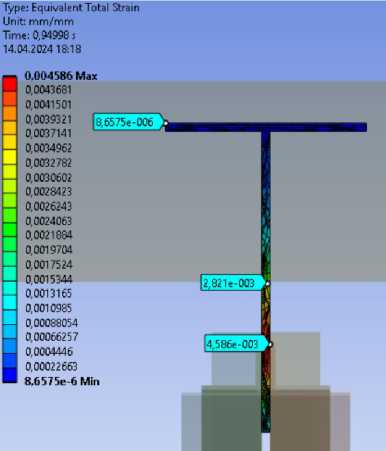
Рис. 19 – Относительные деформации (a – верхний пояс, b – нижний пояс)

Fig. 19 – Equivalent strain (a – upper belt, b – lower belt)

b.

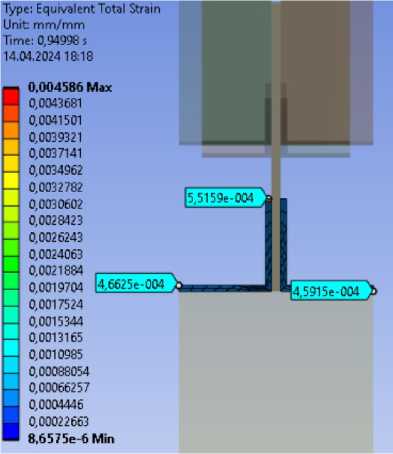
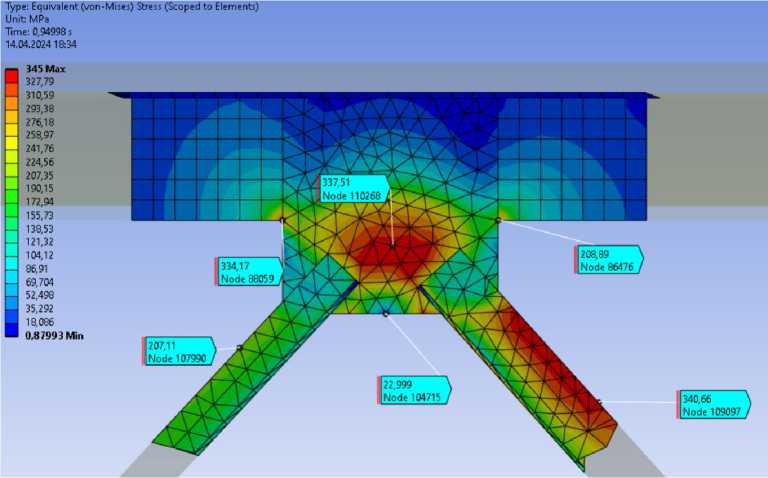
Рис. 20 – Эквивалентные напряжения в узле над опорным раскосом

Fig. 20 – Equivalent stresses in the node above the support brace

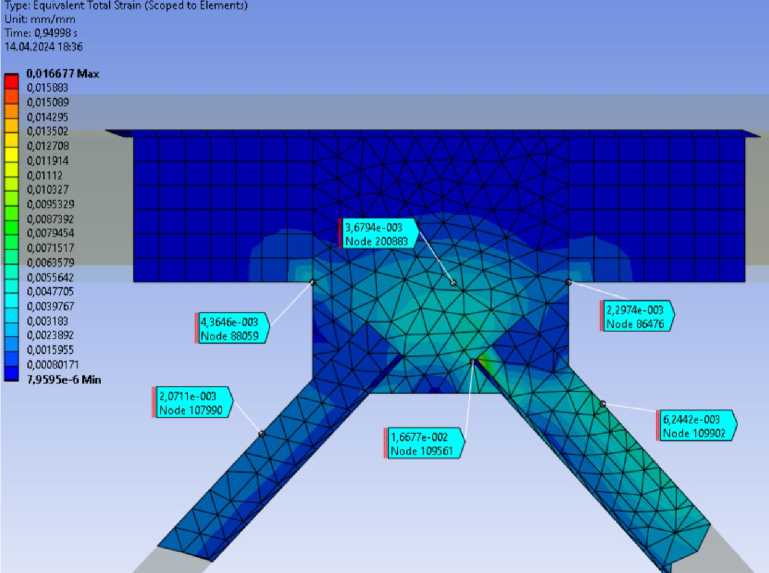
Рис. 21 – Относительные деформации в узле над опорным раскосом

Fig. 21 – Equivalent strain in the node above the support brace

На основе анализа напряженно-деформированного состояния композитной фермы можно сделать вывод, что отказ сечения происходит на участке опорного раскоса вследствие потери устойчивости. Остальные раскосы работают упруго. Нижний пояс фермы находиться на площадке текучести. Тавровое сечение, разгружено работает упруго и обеспечивает совместную работу с железобетонной плитой. Железобетонная плита работает по неразрезной схеме вдоль фермы. В растянутой зоне бетона усилия воспринимает арматура.

Предельный изгибающий момент, воспринимаемый композитной фермой численным методом в ПК Ansys [ansys.com] Mutt,a = 1163.8 кН • м. По формуле (1) Muit = 1224.36 кН • м. Несущая способность по нелинейной деформационной модели Мииндм = 1190.98 кЮм. Расхождения в полученных результатах определение несущей способности композитной фермы в пределах 5%. Наибольшие расхождения с результатами по формуле (1) произошло в следствии недоиспользовании несущей способности на сжатие железобетонной плиты в расчете ПК Ansys [ansys.com].

Для сравнения несущей способности выбраны: 1) исследуемая композитная ферма; 2) металлическая ферма совместно с профилированным настилом [25]; 3) металлическая ферма совместно с железобетонными сборными плитами [26].

Расчет для 2 и 3 образца выполнен в упругой поставке сечения и характеристики материалов заданы такие же, как у исследуемого сечения. Несущая способность 2-го образца P _ult = 28.8 • 1.22 = 35.14 т . Несущая способность 3-го образца P _ult = 28.8 • 1.15 = 33.12 т .

Из анализа несущей способности видно, что исследуемая композитная ферма в 1.24 раза превосходит ферму 2-го образца и в 1.31 раза ферму 3-го образца.

Можно сказать, что при использовании композитной фермы: 1) увеличивается несущая способность; 2) происходит экономия материалов, не требуется установка гибких упоров и других элементов для обеспечения совместной работы фермы и железобетонной плиты; 3) происходит экономия материалов, не требуются горизонтальные связи для раскрепления верхнего пояса фермы.

• 4    Conclusions

На основании проведенных исследований композитной фермы позволили прийти к следующим выводам:

• 1.    Описаны достоинства предложенного варианта композитной фермы. На основе напряженно-деформированного состояние определен характер разрушения сечения, который происходит при потере устойчивости опорного раскоса.

• 2.    Проанализировано напряженно-деформированное состояние. Применены актуальные теории поведения бетона и стали. Определена высота сжатой зоны сечения.

• 3.    Предложены эпюры нормальных напряжений на участке изгибающего момента для исследуемой композитной фермы.

• 4.    Выполнено сравнение с известными металлическими фермами с разными настилами.

• 5.    Авторами намечены дальнейшие исследования: рекомендации по оптимальному конструированию сталежелезобетонной фермы, испытания сил сцепления между сталью и бетоном.

• 5    Conflict of Interests

The authors declare that there is no conflict of interest. The authors made equivalent contributions to the publication.