Численный анализ многократного рассеяния акустической волны на множестве звукопроницаемых сфер в трехмерном пространстве

Исследование рассеяния звуковой волны на препятствиях малых размеров имеет важное значение как для изучения самой природы данного явления, так и с точки зрения практического использования. Рассеяние лежит в основе многих применений акустических волн, таких как гидролокация [1, 2], зондирование атмосферы и океана [1–3], неразрушающий контроль металлоизделий [4], сканирование в медицине [5, 6], создание позиционируемого 3D звука (выделение из множественного звукового потока индивидуального потока и нахождение в 3D пространстве его местоположения) [7], управление звуковыми волнами, переносимыми водой с помощью метаповерхностей (поверхностей, способных менять направление движения звуковых волн, фокусировать их, ограничивать их пропускание или менять частоту, например, за счет содержания полостей) [8–10] и организация микроструктуры в случайных средах [11, 12]. При встрече с множеством препятствий волны звука, рассеченные каждым из них, рассеиваются повторно и многократно другими препятствиями, то есть имеет место образование дополнительных звуковых полей, поэтому задача определения основных характеристик процесса — полного и позиционного сечений рассеяния, сечения обратного рассеяния и другого, является актуальной и важной. Ее решение позволит установить, при каких параметрах системы взаимодействие между частицами существенно и им нельзя пренебрегать или, наоборот, незначительно, и достаточно анализировать множество одиночных частиц. Основные характеристики рассеяния волн на одиночном сферическом препятствии, хорошо отражены в научной литературе [13–22]. Обзор исследований до 1950 г. содержит работа [13]. Следует отметить классическую работу [14], в которой авторы одними из первых для интерпретации рассеяния на одиночном препятствии рассмотрели полное сечение рассеяния (scattering cross section). Теоретические результаты для одиночных газовых пузырьков в воде, достаточно подробно изложены в обзорной работе [15] и монографии [16], а также в статьях [17, 18], где основное внимание уделено резонансным свойствам пузырьков. Одной из первых работ, которая позволяет получить формулу для определения полного сечения рассеяния на идеальной (звуконепроницаемой) жесткой сфере, является работа [19]. Наиболее полно выражения и анализ основных характеристик рассеяния плоской волны на идеальных и звукопроницаемых одиночных сферах представлены в [16]. По аналогии с этой работой в [20] и [21] дается вывод формулы полного сечения рассеяния для случая падения сферической волны от монопольного источника излучения на одиночные звуконепроницаемую и звукопроницаемую сферы соответственно, а также расчет данной характеристики в зависимости от основных параметров системы «окружающая среда–сфера». Заслуживает внимания также работа [22], где найдено выражение сечения рассеяния на движущейся жесткой сфере малого радиуса с постоянной скоростью, много меньшей скорости звука, в приближении малых волновых радиусов.

Ряд публикаций посвящен отысканию основных характеристик рассеяния волны на паре сфер. Теоретическая работа [23] является одной из первых, где с помощью теорем сложения для сферических волновых функций [24] получено выражение сечения рассеяния для двух акустически жестких или мягких сфер одного и того же радиуса при падении плоской волны. Численные расчеты сечения обратного рассеяния и его аппроксимации на бесконечности содержит работа [25] при рассмотрении системы двух сфер с различными краевыми условиями на их поверхностях в зависимости от расстояния между сферами и угла падения плоской волны. В работе [26] представлены результаты расчета интегрального сечения рассеяния плоской акустической волны на двух близко расположенных импедансных сферах, а в работе [27] — выражение сечения рассеяния для системы из двух пузырьков в приближении, что расстояние между центрами пузырьков меньше длины волны. В части работ исследуется величина, называемая формфункцией (form function), которая определяется как квадратный корень из соответствующего сечения рассеяния. Так, например, в [28] численно анализируется формфункция для обратного рассеяния в случае пары взаимодействующих звуконепроницаемых сфер в широких частотных диапазонах (от средних до резонансных значений), а также при расстояниях между сферами в интервале от очень близких, когда сферы соприкасаются друг с другом, до удаленных. Численные расчеты формфункции на бесконечности для системы двух жестких сфер в зависимости от волнового радиуса для различных расстояний между сферами приведены в работе [29], где также сравниваются величины формфункций для двух сфер из нержавеющей стали в воде, установленные экспериментально и теоретически. Аналитические выражения для формфункции системы, состоящей из двух сфер (как проницаемых, так и непроницаемых), одна из которых имеет акустически малый радиус, получены в [30]. Особо следует отметить экспериментальную работу [31], в которой представлены результаты определения обратного рассеяния звука от системы двух воздушных пузырьков в воде. С ними автор настоящей работы сравнивал свои расчетные данные и получил хорошее согласование. Существующие работы, направленные на нахождение сечений рассеяния от множества (более двух) сфер либо сводятся к случаю одиночной сферы, либо ограничиваются рассмотрением некоторых упрощенных случаев. Так, в работе [32] задача рассеяния на множестве воздушных пузырьков сведена к рассеянию на сфере, заполненной пузырьками воздуха различных радиусов, имитирующей промысловый косяк пузырных рыб ограниченных размеров, и численно исследовалось сечение обратного рассеяния данной сферической (одиночной) двухфазной области, а в [33] подобным образом определялась величина эффективного поперечного сечения поглощения сферической волны. В статье [34] представлены численные расчеты обратного сечения рассеяния для простых кластеров из двух и трех пузырьков в различных конфигурациях и при разных углах падения плоской волны. В работе [35] выводится формула для полного сечения рассеяния для множества пузырьков в приближении, позволяющем пренебречь обратным рассеянием между отдельными препятствиями, в результате чего формула сводится к выражению полного сечения рассеяния для одиночной звукопроницаемой сферы, содержащей рассматриваемую систему пузырьков.

Анализ литературы по определению основных характеристик рассеяния показал, что в настоящее время нет формулы, по которой можно вычислить полное сечение рассеяния звука на системе, состоящей из множества сфер, с учетом многократного рассеяния между препятствиями.

Целями настоящей работы является вывод явной формулы для полного сечения рассеяния на множестве взаимодействующих звукопроницаемых сфер, а также численный анализ многократного рассеяния на системах сфер, расположенных в базовых конфигурациях, включая конфигурацию, рассмотренную в экспериментах [31], где пары сфер (воздушные пузырьки) находятся на одном расстоянии от источника монопольного излучения.

2.    Постановка задачи и основные уравнения

Рассматривается акустическое рассеяние на системе N звукопроницаемых сфер различных радиусов a1,a2,., aN , произвольным образом распределенных в бесконечном трехмерном пространстве, заполненном однородной средой, при воздействии внешнего поля. В декартовой системе координат Oxyz центры сфер имеют координаты г = (xv, yv, zv) (v = 1,.., N).

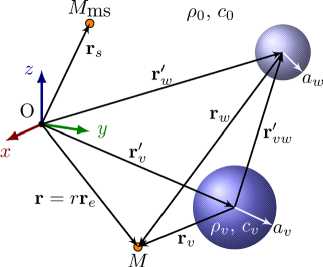
Рис. 1. Схема задачи и основные обозначения в разных системах отсчета

Окружающая среда характеризуется плотностью ρ₀ и скоростью звука c ₀ , среда внутри сфер — плотностью ρ _v и скоростью звука c_v . Внешнее поле в виде сферической волны создает монопольный источник излучения, расположенный в точке M ms ( x ms , У _ms, z _ms ) пространства. Схема для системы сфер и основные обозначения представлены на рисунке 1. Предполагается, что центры сфер неподвижны и отсутствует радиальное движение сферической поверхности.

Задача рассеяния звука на множестве звукопроницаемых сфер сводится к решению уравнений Гельмгольца для комплексных потенциалов у ( г ) (вне сфер) и у ⁽ Пt ) (внутри v -й сферы) [16, 36]:

В формуле (1) k ₀ и k_v — волновые числа для сред вне и внутри сфер.

Потенциал внешнего поля представляется как сумма потенциалов падающего поля — y_in ( г ) , и поля рассеяния — y_scat ( г ) , [34, 37]:

У ( ^г ) = y in ( ^г ) ⁺ У scat ( ^г ) .                                                  ⁽²⁾

Поскольку потенциал поля рассеяния удовлетворяет первому уравнению Гельмгольца в (1), а также условию излучения Зоммерфельда [38], соответствующему затуханию волны на бесконечности, его общее решение определяется как [36]

N со n

V s., ( г ) = xxz A n^{v 1} " s m ( г . ) .

v = 1 n = 0 m =- n

Здесь: а П ^v ) ^m — коэффициенты разложения по мультиполям; S " ( г . ) = h_n ( k 0 r_v ) Y n" ( 9 . ,ф . ) — мультиполь порядка n и степени m ; h n ( z ) — сферические функции Ханкеля 1-го типа; Y n" ( 9 . ,ф . ) — ортогональные сферические гармоники, вычисляемые по формуле:

Y m ( 9,ф ) = ( - 1 ) m 2^ ( n-m ) ! P ( cos9 ) e m ^ф , V 4n ( n + | m |) !

где P nm ( ц ) — присоединенные функции Лежандра [39]. В соответствии с методом повторного разложения по мультиполям [34, 37] коэффициенты A ⁽ v ) m находятся из решения системы линейных уравнений, которая для рассматриваемой задачи записывается в следующем матричном виде [36]:

LA = D ,

где

A = { A u ) = ( A">_. , A ' " • ) = ( { A } T , _ { A ( ' ¹ * } T )’ ,

A u 0

D—I D}

= ( D ^{( 1 )} , . , D ⁽ N ) ) = ( { D^{1 m} } ^T , _ , { D nN ) m } ^T ) ,

	' L ( 11 )	L ( 12)     •	. L^1 N ) ^		' ( C} I L U2 ) } •	■ I L UN ’ )'
L — { L u . t . } —	L ( 21 )	L ( 22)    •	„  L( 2 N )	—	{ Lc. ; ’ } I L; ?}	■ I L uN ’}
	l ( N 1 )	L ( N 2 )   •	• •   l( NN )v		. I L ( N 1 ' } I L ( N ’ ’ } •	■ I C ’},

, jn (k0aw ) jn (kwaw ) - Kwjn (k0aw ) jn (kwaw )

—

= A v ) s ,     D^ — D n ^w ) m —

h (kna ) j (ka ) — к h (k„a ) j (ka )

n 0 w n ww wn 0 w n ww

m '

in, n ( r w ) ,

( у ( ^г )^- V⁽n v t)|_r__a = 0,

1 dy 1 dy v — Р о ^d Г P v 0 r

= 0,

v = 1, ., N .

v

Jl ( ^k 0 a w ) J l ( k w a w ) ^{— к} w Jl ( ^k 0 a w ) Jl ( k w a w )/_с mV™/ • \

L u ₀ t ₀

- j ( wv ) _ “ i t i

, , Ът7----A-----, ,----'    ,----7 ( 5 I R X, (rvw )     для v * w, hl ( k0 aw ) jl ( kwaw )-K whl ( k0 aw ) jl ( kwaw )

I5U1t1      для v — w, u 0 — ( v — 1)( n tr + 1) +(l + 1) — (l — s ) , 10 — (w —1)( ntr +1)2 +(n +1)2 — (n — m), l — 0,1,., ntr;     s — — l,., l;     n — 0,1,., ntr;

U i — ( / + 1 ) — ( / — s ) , t₁ — ( n + 1 ) 2 — ( n — m ) , m — — n , . , n ;     v , w — 1, . , ' .

Здесь: J_n ( z ) и J l ( z ) — сферические функции Бесселя 1-го типа и их производные [39]; к _w — ( k ₀р _w )/( k w р₀ ) — введенный параметр; C i^n ( r w ) — коэффициенты разложения потенциала падающего поля y in около r — r w ; ( 5 | R ) _/n (r _izw ) — коэффициенты перехода при повторном разложении по мультиполям [37]; 5 _u t — символ Кронекера; n _tr — число членов ряда после его усечения. Важно, что при численной реализации решения система уравнений (3) должна быть конечной, поэтому необходимо проводить усечение рядов при разложении по l и n . Вопрос выбора числа n _tr при усечении рядов, используемых в настоящей работе, будет рассмотрен далее, в разделе 4.

3.    Формула полного сечения рассеяния для системы взаимодействующих сфер

Величина полного сечения рассеяния σ_s определяется как отношение мощности рассеянной волны P _scat к интенсивности падающей волны I ₀ (см., например, [16, 41]), то есть

P

« . — -у- — у J Is-d⁵ , I 0 I 0 ( 5 )

где I scat — интенсивность рассеянной волны; интеграл берется по сферической поверхности 5 — 4п r ² радиуса r , окружающей препятствие. Физический смысл величины σ_s — это площадь перпендикулярной потоку области (круга), попадая в которую налетающая волна испытывает рассеяние.

Для одиночной звукопроницаемой сферы σs вычисляется по формуле [21]:

co

O s = B 0 £ ( 2 I + 1)1 B, Г ,

I = 0

в которой коэффициенты для монопольного источника излучения имеют следующий вид:

B ₀ = 4n d ²,

B = j ( k о a ) j ( ^k i a ) - К /' 1 ( k о a ) j ( k i a ) h ( k d ) l h ( k о a ) j ( k i a ) -« h 1 ( k о a ) j ( k a ) ^{1 0 .}

Чтобы найти полное сечение рассеяния для системы, состоящей из множества сфер, нужно знать интенсивность рассеянной волны. Она определяется как [16]

I = Ref p   • v_r2 .

scat              scat     r s

Здесь: v r, = ( d p scat д r )J( ii mp₀ ) — колебательная скорость рассеянной волны в радиальном направлении; д p d rr — частная производная функции p по переменной r ; знак «*» в верхнем индексе обозначает сопряженную величину. Интенсивность падающей волны равна 1 ₀ = | p ₀|² Д2р₀ c ₀ ) , где p ₀ — давление в дальнем поле. Связь между акустическим давлением p и потенциалом у имеет вид: p = р₀ ( б у/д t ) = i юр₀у.

C учетом формулы (4) и асимптотик для сферической функции Ханкеля и ее производной по аргументу k 0 r v при k 0 r , . o [39]

hn ( k 0 rv )| k0 r, .o = (-1) n+1 ^0 rV /( k0 rv ) ,     hn ( k 0 rv )|kr ... = ihn ( k0 rv ) , а также асимптотики для экспоненты [34]

ik„r,               ik0 ( r-rv •re )/ e 0 v / rv « er где re — единичный вектор вдоль направления рассеяния, получаются следующие выражения:

ik 0 r N o n‘ a- = 7°—ZZ Z An* (-1)•+1 e-0|rv"’y: (»,Ф), k 0    r v=1 n=0 m=-n ik0 r N o 1

v r s = — ZZZ A w ) ¹ ( - i ) ¹ e ik ^{0 (} r v" ) Y 1 s ( °,Ф ) .

r w = 1 1 = 0 s =-

После их подстановки в формулу ( 6 ) и некоторых преобразований следует формула для интенсивности рассеянной волны:

1 mn ( N o n o l                               * j ‘ x                         \

I scat = 77^ 2- Re ZZZZZ ( - 1 ) n i n ⁺ l An ^v ) m ( A^ w ) s ) e i ^{0 (} r vw ") Y m ( 9,Ф ) Y? * ( 9,Ф ) | .

² k 0 r      \ v , w = 1 n = 0 m =- nl = 0 s =- 1                                                                    )

Можно видеть, что все величины в ее правой части являются известными, поскольку коэффициенты а П ^v ) ^m определены из решения системы линейных уравнений (3).

С учетом ортонормированности поверхностных сферических гармоник и соотношения

Y₁ ^s * ( 6,ф ) == ( - 1 ) s Y₁ ^{- s} ( 6,ф ) [39], значение полного сечения рассеяния (4) преобразуется к следующему виду:

Л

σ

s

ωρ₀ 2 k 0 I 0

N o n          2      1           N o n o l                                  *

ZZZ A nv ' " | + ^Re ZZZZZ ( - 1 ) ^{n +} "-'■ ⁺ l A n^{v 1} " ( A lw ¹ ■ ¹ v = 1 n = 0 m =- n             ^4П       v , w = 1 n = 0 m =- nl = 0 s =- 1

d v * w

X ( 2 n + 1)( 2 I +1 )

• Int⁽ vw ’ ms Int nl '

(vw’ ms где в правой части интеграл Intnl    равен:

2ππ'

Int nw ’ ms = J e i" ^- s ^{) ф} J e '¹ 0 ^(r"^{T e} ’ P n" ( cos9 ) p s ( cos9 ) sin9d9d_V.

В осесимметричном случае, подробно рассмотренном в работе [42], когда центры всех сфер располагаются на одной оси, которая к тому же является координатной осью O z , выражение интеграла в правой части упрощается:

π

Int nvw ’ ms = 2n§ ms ( - 1 ) - m J e i⁰r w ^cos9 p nm ¹ ( cos9 ) P m ( cos9 ) sin9d9.                         (9)

Для записи интегралов (8) и (9) в явном виде следует применить формулы разложения произведения двух присоединенных функций Лежандра и интегрального представления волновых функций (см., например, работу [24]):

P nm ( cos9 ) P ls ( cos9 ) = n T b ( n^nm1s ’ P im ^{- s} ( cos9 ) ,

' i =1 ^{n - 1}

J e m ^e J ek ° n - ^R p nm ( cosa ) sinadadp = 4n i ⁿ j_n ( к ₀ r ) P nm ( cos9 ) e '" ^ф , 00

где b 'ⁿ"^1s ’ — коэффициенты Клебша-Гордана, значения которых могут быть вычислены, например, как в книге [24]; векторы n и R имеют сферические координаты ( 1, a,P ) и ( r , 9,ф ) . Тогда с учетом свойства присоединенных функций Лежандра:

р - ^т(т\-1 |Г ^{( n -} " ’ ! т"ЧЛ

^P- ⁽ * ^,"^{( - 1 )} ( n * " ) ! ^{P (} * ’ '

для полного сечения рассеяния (7) получаются следующие выражения: – в общем виде

σs

ωρ₀ 2 k 0 I 0

r

N да n . _l9 +++ A n^v ’ " l v = 1 n = 0 ■ =- n

r

N да n да 1

* Re ZZZZZ ( - 1 ) n * " i n * ¹ A n v ’ m

к

v , w = 1 n = 0 m =- n 1 = 0 s =- 1 к v * w

*

( A ( w ) s ) x

X ( 2 n +1 )( 2 1 +1 )

c ( ^m ' ^s ) e i ( ^{m - s} ) ф vw

n + 1

+ b<^nm1s ’ i i j 1 ( к 0 r w ) P ”- ^{- s} ( cos9 vw )    ;

' 1 =1 ^{n -} l

– в осесимметричном случае o = ^Pk s    2k0I0

r

N да n .         .9

+++ A nv ’ " I + Re v = 1 n = 0 ■ =- n

к

r

N да n да                                         *

SEZK-1)n * "in * 1A^1 ■ (Ai"’") x v' w =1 n=0 ■=-n I=0

к v * w

x, ( 2 n +1 )( 2 1 +1 ) ( n ^-| m l) ' < 1 ^- m ) ! + + : b_:™m - i i j ( к 0 r vww ) I 11 vw

В формуле (10) коэффициенты c ⁽ m ’ ¹ ) определяются из следующих выражений:

	[ 1,	для	m >  0	и	s >  0;
	ш ( n + m )!
	( -1 ) ” 7—kk,	для	m <  0	и	s >  0;
	( n - m ) !
c ( m ’ s ) _	( n- s ( l + 1 s i) ! ( 1)              l\i,	для	m >  0	и	s <  0;
	( l - s ) !
	(-1)-| m |-I s | ( n + I m l) ! ( 1 + I s l) !	для	m <  0	и	s <  0
	[( )         ( n - | m |) ! ( l - | s |)!

Интенсивность падающей сферической волны от монопольного источника излучения на системе сфер может быть вычислена как

I _ юроVo k0 0   32π2dM2s где ю _ 2пf — угловая частота, f — частота внешнего поля, Vo — производительность монопольного источника излучения, dms — расстояние от монопольного источника Mms до геометрического центра системы сфер.

4.    Численные результаты

Расчет полного сечения рассеяния по формулам (10) или (11) осуществляется с помощью разработанного автором программного кода на языке Fortran 90 для Windows со стандартной сборкой компиляторов (GCC) в среде MSYS2 (MinGW-w64) c подключением библиотеки LAPACK [43] для решения системы (3). Специальные сферические функции h_t ( z ) , j_t ( z ) и присоединенные функции Лежандра P ls ( z ) и их производные вычислялись с помощью адаптированных программных кодов, написанных на языке Fortran 77 для специальных цилиндрических функций и полиномов Лежандра [44]. Вычислительные эксперименты проводились в ОС Windows 10 на процессоре Intel Core i7-4702MQ (4 ядра и 8 потоков по 2,2 ГГц, кэш 6 Мб) с 32 Гб ОЗУ. Затраченное на выполнение программы общее время t_cpu определялось консольной командой time .

Ряды, использовавшиеся при разложениях, являлись сходящимися. При проведении вычислительных число членов ряда при усечении ( ntr ) выбиралось таким образом, чтобы обеспечивалась заданная точность δfix в соответствии с подходом, изложенным в [40], то есть когда относительная погрешность двух последовательных значений суммы искомого ряда (Еi и Еi+1) становилась меньше 5fix :

|( Е i - Е i _{+ 1} ) /Е n | -100 % <  5_fix , число n tr полагалось равным i : n _tr _ i .

Рассматривалась бистатическая акустическая система, воздействующая на пару рассеивателей, что соответствовало лабораторным экспериментам, представленным в работе [31]. Это позволило провести верификацию авторского общего численного алгоритма [36], примененного в настоящей работе для отыскания полного сечения рассеяния системы.

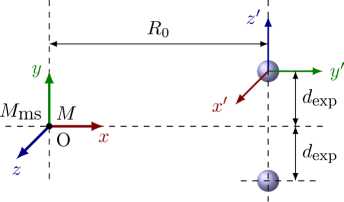
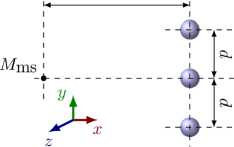
Рис. 2. Схема эксперимента с парой рассеивателей (воздушных пузырьков) [31] и обозначения основных параметров; системы координат: O xyz – общий алгоритм [36], O x ' y ' z ' – осесимметричный алгоритм [42]

В экспериментах [31] исследовалась пара воздушных пузырьков в воде, помещенных на очень тонкую нить на одинаковом расстоянии от комбинированного луча двух, лежащих на одной оси преобразователей. Один из преобразователей являлся источником акустической волны (монопольный источник в точке M _ms ), а второй — приемником рассеянной волны (в расчетной точке M ). На рисунке 2 показаны схема эксперимента и обозначения основных параметров. Значения физических параметров (плотности ρ и скорости звука c ) приведены в таблице 1; геометрические параметры, использованные при расчетах, были

Таблица 1. Значения физических параметров при 20ºС

Вещество	р , кг/м3	с , м/с
Воздух	1,205	343,1
Вода	998	1484
Дихлорэтан	1252,6	1034

следующими: расстояние между преобразователями равнялось нулю (в представленных экспериментах M = M ms ), ось, соединяющая центры пузырьков, отстояла от преобразователей на расстоянии R 0 = 0,58 м; внешнее поле имело частоту f = 80 и 140 кГц; радиусы пузырьков составляли a 1 = a 2 = a = 585 ± 35 мкм.

На рисунке 3 а для сравнения изображены данные лабораторных (см. символы) [31] и вычислительных (линии) экспериментов для функции

TS = 20 lg

У ( r i ) r

V in ( Г ) ¹ ’

выраженной в децибелах, которая характеризует обратное рассеяние в точке M = M ms . Следует отметить, что для расчета полного потенциала (2), который используется в последней формуле, к решению системы уравнений (3) применен общий оптимизированный алгоритм [36], позволяющий найти коэффициенты разложения потенциала поля рассеяния. Общее время расчета t_cpu при числе усечения рядов n tr = 10, отвечающем условию 5 fix = 10 - 4 %, и шаге по k ₀ d exp , равном A h = 0,05, составляет 4,21 с. Поскольку в экспериментах образовывались пузырьки среднего радиуса a = 585 ± 35 мкм, то каждая пара линий (сплошных или штриховых) устанавливает верхнюю (при a = 620 мкм) и нижнюю (при a = 550 мкм) границы для соответствующих экспериментальных данных. Видно, что численные данные качественно и количественно согласуются с экспериментальными. Отметим, что для пары пузырьков также может быть использован упрощенный осесимметричный алгоритм, рассмотренный в работе [42], если в качестве оси O z выбрать ось, соединяющую центры сфер. При этом общее время расчета сокращается: t_cpu = 0,82 с.

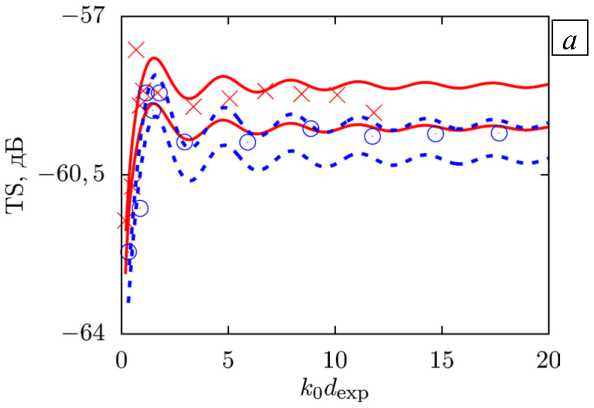
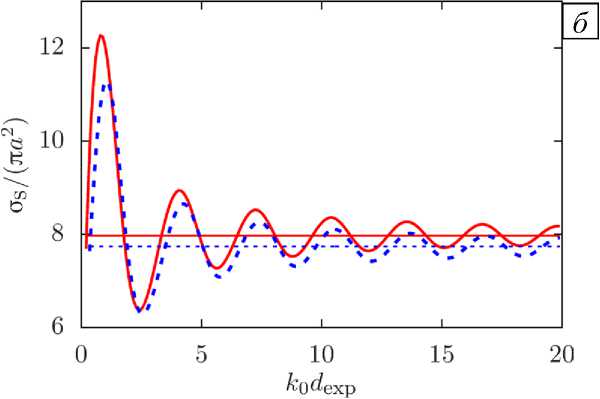
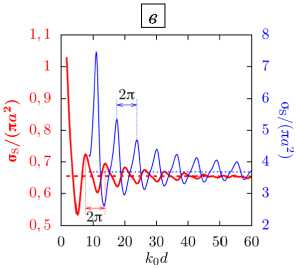
Рис. 3. К сравнению расчетных (линии) и экспериментальных (символы) [31] данных при a = 585 ± 35 мкм ( а ) и нормированное полное сечение рассеяния a s Дл a ² ) для a = 585 мкм, рассчитанное по формуле (11) ( б ); зависимости построены для двух воздушных пузырьков в воде при монопольном источнике излучения с разной частотой f , кГц: 80 (сплошные линии и крестики) и 140 (штриховые линии и кружки); горизонтальные линии на ( б ) ‒ суммы значений a s Дл a ² ) , полученные согласно формуле (5) для двух одиночных невзаимодействующих пузырьков

Для численного анализа эффектов многократного рассеяния вводились обозначения: о- ио- — значения полного сечения рассеяния с учетом и без учета взаимодействия между сферами. При этом о-определялось по формуле (10) (в общем случае) и (11) (в осесимметричном случае), а о- имело вид суммы значений одиночных сфер (5). Относительное отклонение величины о- от о- задавалось как о + -о

5 = -s----s- - 100 %.

—

о

На рисунке 3 б для сравнения представлено нормированное значение

■ _sДл a ² ) c величиной о_s, рассчитанной по формуле (11) (о - ) при

полного сечения рассеяния среднем радиусе пузырька

а = 585 мкм. Горизонтальные прямые показывают нормированное значение полного сечения рассеяния в случае невзаимодействующих пузырьков (а - ).

Следует отметить, что когда отношения упругостей вещества сферы (х v = р v c 2 ) и внешней среды (X 0 = Р 0 с 2 ), а также отношения плотностей внутренней (р _v ) и внешней (р₀ ) сред стремятся к бесконечности (X _v /х₀ ^да и р _v /р₀ ^ да ), то имеет место согласование со случаем малых мягких сфер (см. например [16]), причем для воздушных пузырьков согласование возможно вне области резонанса (при k ₀ а » 0,013). Для одиночных мягких сфер при малых волновых числах ( к ₀ а ^ 1 ) значение a s Д п а ² ) ® 4, а для пары сфер при к ₀ а ^ 1 и к ₀ d exp » 1 в работе [23] получено, что значение a s Д п а ² ) ® 8 . Если посмотреть на рисунок 3 б , то для пары воздушных пузырьков при f = 80 кГц, для которой к ₀ а ® 0,2, также можно видеть, что значение a s Д п а ² ) ^ 8 при k ₀ d exp ^ да . Это согласуется с результатами для пары мягких звуконепроницаемых сфер (см. [23]).

На рисунке 4а представлен характер безразмерного значения as Д па2), когда рассеивателями служат две капли воды в воздухе, для которых выполняются условия: хv/х0 »1 и рv/р0 »1. Это согласуется со случаем малых жестких сфер. Для малых волновых чисел к0а ^ 1 одиночная жесткая сфера имеет сечение рассеяния asДпа2)~(7/9)(к0а)4, которое во много раз меньше ее геометрического сечения [16]. Расчеты для пары капель воды в воздухе показали, что при к0а ^ 0 и k0dexp ^ да безразмерное сечение рассеяния составляет asДпа2 ) да (14/9)(к0а)4, то есть стремится к сумме сечений рассеяния на двух одиночных жестких сферах. Вычислительный эксперимент по рассеянию коротких волн (к0а »1)

при k0dexp ^ да показал, что как для пары воздушных пузырьков воде, так и для пары капель воды в воздухе сечение рассеяния as Дпа2 )^ 4

что также согласуется с результатом для одиночных мягких и жестких сфер, при которых as Дпа2 )^ 2 [16].

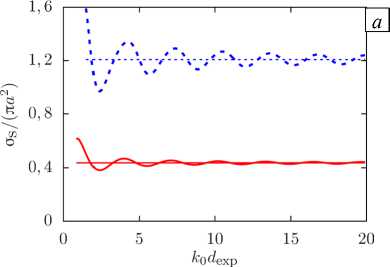
Рис. 4. Нормированное полное сечение рассеяния a s Д п а ² ) , рассчитанное по формуле (11), для капель воды в воздухе ( а ),

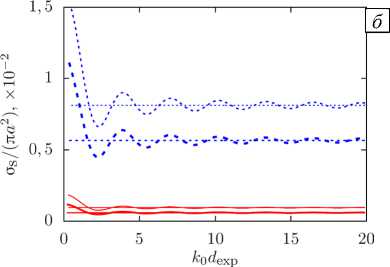
капель дихлорэтана в воде (толстые линии) и капель воды в дихлорэтане (тонкие линии) ( б ) в зависимости от параметра k ₀ d _exp при а = 585 мкм и монопольном источнике излучения с разной частотой f , кГц: 80 (сплошные линии) и 140 (штриховые линии); горизонтальные линии - суммы значений a s Дп а ² ) при двух одиночных невзаимодействующих каплях, рассчитанные по формуле (5)

На рисунке 4 б представлены промежуточные случаи: капли дихлорэтана в воде ( х _v /х ₀ ~ 0,6 и р v /р₀ да 1,3, толстые линии) и капли воды в дихлорэтане ( х _v /х₀ ~ 1,6 и р _v /р₀ ® 0,8, тонкие линии). При данных параметрах рассеяние от пары капель жидкости, помещенных в другую жидкость, незначительно. При k ₀ d exp ^да значение a s Д п а ² ) для пары взаимодействующих капель также стремится к сумме значений данной величины для двух невзаимодействующих звукопроницаемых капель.

Из рисунков 3 и 4 видно, что наибольшее по абсолютной величине рассеяние имеет место в системе с воздушными пузырьками в воде, где модуль отклонения δ относительного сечения рассеяния при частотах 80 и 140 кГц в точках максимума (при k0dexp , равном 0,79 и 1,03) составляет 53,82 и 46,02%, а в точках минимума (при k0dexp , равном 2,38 и 2,51), соответственно 19,72 и 18,76%. Наименьшее по абсолютной величине рассеяние наблюдается в системе с каплями дихлорэтана в воде, но при этом модуль отклонения δ в точках максимума и минимума становится больше: при частотах 80 и 140 кГц в точках максимума (при соприкосновении сфер) отклонение, соответственно, достигает 98,82 и 95,91%, а в точках минимума (при к0dexp = 2,28 и 2,21) — 20,86 и 20,73%. В случаях воздушных пузырьков в воде, капель дихлорэтана в воде и капель воды в дихлорэтане модуль отклонения δ не превышает 5% при к0dexp > 9 и не зависит от частоты, а для капель воды в воздухе — при к0dexp > 5,7 и f = 80 кГц, при к0dexp > 9,2 и f = 140 кГц. Таким образом, для разных сред вокруг и внутри сфер получено, что эффектами многократного рассеяния при близком расположении препятствий (в общем случае при к0dexp < 9,2 ) пренебрегать нельзя.

В трехмерном пространстве представляет интерес система из трех ( N = 3 ) звукопроницаемых сфер для четырех базовых конфигураций (I–IV) , в которых центры первой и третьей сфер смещаются вдоль оси O y в противоположных направлениях, а центр второй сферы располагается по-разному (Рис. 5 а ):

• ‒    в конфигурации I зафиксирован и лежит на одной линии с центрами первой и второй сфер;

• ‒    в конфигурации II движется вдоль оси O x к монопольному источнику излучения M _ms ;

• ‒    в конфигурации III удаляется по оси O x от монопольного источника излучения M _ms ;

• ‒    в конфигурации IV из своего первоначального положения сдвигается по оси O z .

Во всех конфигурациях начало декартовых осей координат совпадало с положением монопольного источника излучения (см. точку M ms ) ; система из трех сфер имела основные параметры: R ₀ = 0,58 м; f = 80 и 400 кГц; радиусы сфер a i = a = 585 мкм ( i = 1, 2, 3). Начальное значение безразмерного параметра k ₀ d ₀ определялось из условия, что сферы соприкасаются.

Вычислительные эксперименты проводились для двух случаев, когда внешняя и внутренняя среды существенно отличались упругостью: воздушные пузырьки в воде и капли воды в воздухе. Для всех конфигураций и заданной точности решения 5 fix = 1% при частоте f = 80 кГц оказалось достаточным число усечения рядов n tr = 8 , а при частоте f = 400 кГц — n tr = 6 для воздушных пузырьков в воде и n tr = 7 для капель воды в воздухе. При шаге по координате к 0 d , равном A h = ( 20 - к ₀ d ₀ ) /200 (с одинаковым количеством расчетных точек в каждом вычислительном эксперименте), общее время расчета ( t_r„„ ) для n„ = 8 составило 85 с, для n„ = 7 — 47 с и для n„ = 6 — 30 с. cpu              tr                                                    tr                                       tr

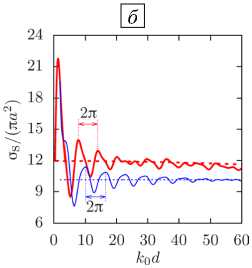
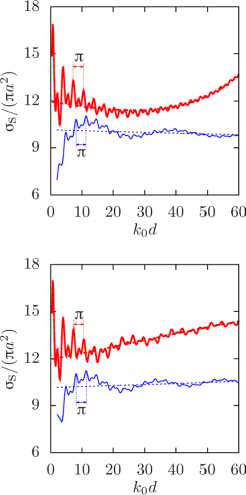
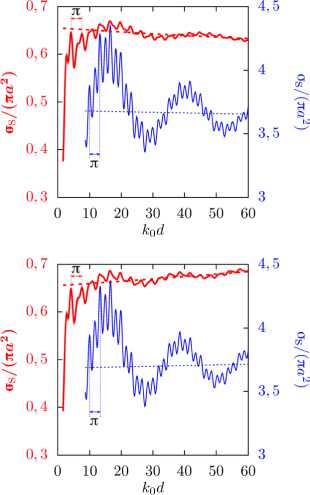
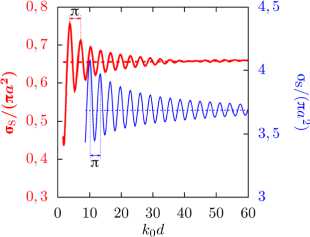
На рисунках 5 б представлены зависимости нормированной величины o s Дп а ² ) от безразмерного параметра k ₀ d для конфигураций воздушных пузырьков в воде с учетом взаимодействия между сферами (о + , толстые линии) для случая, когда полное сечение рассеяния определяется по формулам (11) для конфигурации I или (10) для конфигураций II-IV, и без взаимодействия (о - , тонкие линии). Рисунки 5 в демонстрируют аналогичные графики в случае капель воды в воздухе. В таблицах 2 и 3 приведены следующие данные: k ₀ d ₀ — начальное значение, при котором сферы соприкасаются; значения δ_max и k ₀ d _max , отвечающие максимальному отклонению δ , вычисленному по формуле (12) (максимальный рост рассеяния); значения δ_min и k ₀ d _min , соответствующие минимальному отклонению δ (максимальное падение рассеяния); к ₀ d ₁₀ % и к ₀ d 5% — минимальные значения, начиная с которых выполняются условия |3| <  10% и 15| <  5%. Параметры системы, рассмотренные для конфигураций пузырьков в воде, дают волновые радиусы k ₀ a , лежащие вне монопольного резонанса, и резонансов, возникающих при более высоких частотах [17], то есть эффекты, связанные с резонансом в пузырьковых системах, исключены из исследований.

Анализ численных результатов (см. Рис. 5 и Табл. 2 и 3) показал следующее. Частота колебаний величины полного сечения рассеяния σ_s зависит от конфигурации системы (период колебаний при конфигурации I в 4 раза больше, чем при конфигурациях II и III, и в 2 раза — при конфигурации IV), и на его величине не сказываются физические параметры системы (плотность и скорость звука окружающей и внутренней сред). При одних конфигурациях системы характер многократного рассеяния меняется несущественно (как при конфигурациях II и III), а при других — значительно (как при конфигурациях I, II (или III) и IV). Эффекты многократного рассеяния проявляются максимально в основном на некотором волновом расстоянии k ₀ d между сферами, а при его дальнейшем увеличении эти эффекты затухают. Значение предельного волнового расстояния между центрами сфер k ₀ d , до которого эффекты многократного рассеяния являются существенными, для рассмотренных конфигураций и частот, можно определить с помощью таблиц 2 и 3.

а

Ro

Конфигурация I

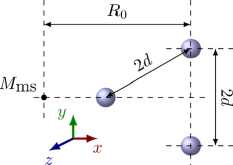
Конфигурация II

Ro

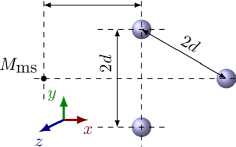
Конфигурация III

Ro

Конфигурация IV

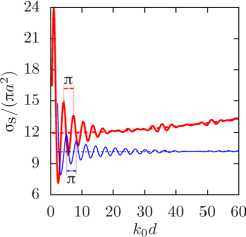
Рис. 5. Схема конфигурации ( а ), зависимость нормированного полного сечения

рассеяния a s Д n a ² ) от безразмерного

параметра k ₀ d для воздушных пузырьков в воде ( б ) и капель воды в воздухе ( в ) для двух значений частоты f , кГц: 80 (толстые линии) и 400 (тонкие линии), с учетом (сплошные линии) и без учета (штриховые линии) взаимодействия между сферами

Таблица 2. Результаты вычислительных экспериментов в случае системы из трех воздушных пузырьков в воде при воздействии монопольного источника излучения с разной частотой f

(в скобках соответствующие значения волнового радиуса k ₀ a )

Конфигурация	f = 80 кГц ( k 0 a = 0,20 )							f = 400 кГц ( k 0 a = 0,99 )
	к d 00	8 ma X , %	k 0 d max	S • , %	k 0 d min	k.d.. 0 10%	k 0 d 5%	к d 00	S max , %	k 0 d max	8 „in , %	k 0 d min	k.d.. 0 10%	k 0 d 5%
I	0,40	82,33	1,39	–28,77	5,16	12,32	49,67	1,98	92,90	1,98	–24,62	6,43	13,39	25,96
II		41,51	0,59	–12,14	2,98	7,55	13,91		9,50	11,26	–31,26	1,98	4,30	15,13
III		41,84	0,59	–11,70	2,98	7,75	15,30		9,82	11,46	–21,85	3,53	4,30	15,13
IV		100,91	0,99	–40,86	2,38	9,14	13,91		45,26	1,98	–21,87	3,14	6,82	14,75

Таблица 3. Результаты вычислительных экспериментов в случае системы из трех капель воды в воздухе при воздействии монопольного источника излучения с разной частотой f

(в скобках соответствующие значения волнового радиуса k ₀ a )

Конфигурация	f = 80 кГц ( к 0 а = 0,87 )							f = 400 кГц ( к 0 а = 4,33 )
	к d 00	8 „a X , %	k 0 d max	5 min , %	k 0 d min	k.d... 0 10%	k 0 d 5%	к d 00	5 max , %	k 0 d max	5 min , %	k 0 d min	k.d 0 10%	k 0 d 5%
I	1,71	57,19	1,71	–18,38	5,02	7,93	17,84	8,57	102,91	10,97	–28,89	13,37	49,20	58,46
II		3,33	16,48	–42,73	1,71	5,60	9,10		18,33	16,46	–8,67	27,43	20,23	42,17
III		3,60	16,48	–40,35	1,71	5,79	9,10		18,47	16,63	–8,55	27,43	20,23	42,17
IV		15,47	3,85	–33,50	1,91	5,79	12,01		10,76	10,11	–6,80	8,57	10,47	19,88

Выявлено, что на скорость затухания влияют расположение сфер, частота излучения монопольного источника и физические параметры системы. Так, для воздушных пузырьков в воде наибольший вклад многократного рассеяния в величину полного сечения рассеяния дает конфигурация IV при f = 80 кГц. Для капель воды в воздухе наибольший рост данной величины относительно случая без взаимодействия сфер имеет место при конфигурации I и f = 400 кГц, а наибольшее падение — при конфигурациях II и III и f = 80 кГц.

Далее рассмотрена конфигурация системы препятствий, представленная в работе [37]: рассеивающий слой, состоящий из N = 11 x 11 = 121 сфер одинакового радиуса a = 1. Сферы равномерно распределены в плоскости O yz с наименьшим расстоянием между соседними центрами , которое равно δ l (см. Рис. 6 а ). Но, в отличие от работы [37], где сферы являются звуконепроницаемыми и жесткими, в настоящем исследовании сферы звукопроницаемы. В связи с этим для возможности сравнения с численными результатами работы [37] выбрана внешняя среда с физическими свойствами воздуха, а внутренняя — со свойствами воды. Монопольный источник излучения M ms ( - 10 а ,0,0 ) располагался на оси O x на расстоянии d = 10 a от плоскости, проходящей через центры сфер, а точка расчета M — на оси O x симметрично точке M _ms . На рисунке 6 б представлены результаты расчета функции

STF = 20lg

ψM ψin M характеризующей рассеяние в точке Mms (-10а,0,0), для волновых радиусов к0а = 1,3,5, полученные в работе [37] при 51 = 5а и фиксированного числа усечения рядов ntr = 5 (закрашенные кружки большого радиуса) для звуконепроницаемых жестких сфер, и в настоящей работе для к0а = 1,5 при 51 = 3а и 5а , а также при

n _tr

, отвечающем

заданной точности 8_& = 1% (см. Табл. 4), (средние и малые закрашенные

б

a

в

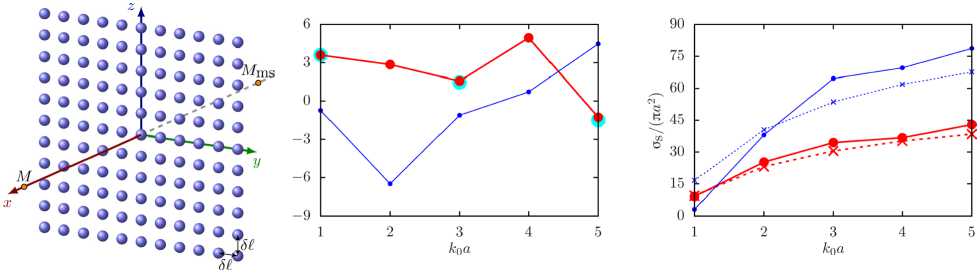
Рис. 6. Конфигурация рассеивающего слоя из капель воды числом 121, имеющих одинаковый радиус и равномерно распределенных в воздухе ( а ); зависимость функции STF в точке M ( 10 а , 0, 0 ) от волнового радиуса к о а , рассчитанная по алгоритму из [36] (толстые и тонкие линии с закрашенными кружками среднего и малого радиуса), и данные для слоя из жестких сфер [37] (закрашенные кружки большого радиуса) ( б ); характер нормированного полного сечения рассеяния o_sДп а ² ) в зависимости от k ₀ a ( в ) с учетом (сплошные линии) и без учета (штриховые линии) взаимодействия между сферами; на фрагментах

(б) и (в) тонкие линии с символами отвечают расстоянию 51 = 3а , толстые линии с символами - 51 = 5а кружки) для капель воды в воздухе. Относительные погрешности авторских результатов, отнесенных к расчетным данным работы [37] составили: 0,19% для k0a = 1; 0,92% для k0а = 3 ; 4,64% для k0а = 5. Увеличение погрешности связано с тем, что с ростом волнового радиуса k0 a требуется большее ntr , при котором достигается устойчивое решение (см. Табл. 4). Следовательно, растет отклонение конечного результата от случая малой жесткой сферы. Таблица 4 также содержит процессорное время tcpu , затраченное на расчет в рассматриваемой точке.

Таблица 4. Значения числа усечения рядов n tr , при котором достигается точность 8 fix = 1% при расчете конфигурации из 121 сферы, и процессорное время t cpu для различных значений 5 1 и к ₀ а

5 1	k 0 a
	1		2		3		4		5
	n tr	t cpu , c	n tr	t cpu , c	n tr	t cpu , c	n tr	t cpu , c	n tr	t cpu , c
3 a	4	38	7	550	9	1430	10	2464	12	6848
5 a	3	12	5	112	8	1165	8	1153	12	6580

Рисунок 6 в демонстрирует результаты расчетов нормированного полного сечения рассеяния o s Дп а ² ) с учетом взаимодействия между сферами. Видно, что для рассмотренных параметров системы учет взаимодействия между сферами является важным, хотя оно и уменьшается с ростом расстояния между центрами сфер: среднее арифметическое отклонение модуля величины δ , определяемой по формуле (12), составляет около 27,3 и 8,4%, соответственно, при 8 l = 3 а и 8 l = 5 а .

5. Заключение

В настоящей работе для анализа многократного рассеяния акустической волны на множестве звукопроницаемых сфер впервые получена явная формула для основной характеристики данного явления — полного сечения рассеяния, учитывающая взаимодействие между сферами в системе. Формула применима для любого числа сфер различных радиусов, произвольным образом расположенных в трехмерном пространстве, и при произвольном внешнем воздействии в границах применимости алгоритмов, используемых для общего [36] или осесимметричного [42] случаев.

На примерах систем сфер, имеющих базовые конфигурации, проведен анализ влияния основных параметров системы (плотности и скорости звука вокруг и внутри сфер, частоты внешнего воздействия, расстояния между центрами сфер, положения сфер относительно друг друга) путем сравнения полного сечения рассеяния, полученного с помощью формул (10) и (11) в общем и осесимметричном случаях, учитывающих взаимодействие между рассеивателями, и формулы (5) без учета взаимодействия.

Вычислительные эксперименты, выполненные с учетом и без учета взаимодействия между сферами, подтвердили, что эффектами многократного рассеяния при близком расположении сфер пренебрегать нельзя, а именно:

‒ для систем из двух сфер, расположенных на одинаковом расстоянии от монопольного источника излучения, данные эффекты для капель воды в воздухе, то есть при выполнении условий % v /% 0 » 1, р v /р₀ » 1 и частоте f = 80 кГц, существенны при волновом расстоянии между центрами сфер k ₀ d exp <  5,7, а для большей частоты ( f = 140 кГц) и других соотношений физических параметров сред (независимо от частоты) — при k ₀ d _exp <  9,2. Дальнейшее увеличение волнового расстояния k ₀ d _exp дает модуль отклонения δ , определяемого по формуле (12), менее 5%;

‒ для систем из трех сфер (воздушных пузырьков в воде и капель воды в воздухе), образующих четыре базовых конфигурации, при частоте излучения 80 и 400 кГц установлена величина предельного волнового расстояния k ₀ d ₅ % , начиная с которого модуль отклонения |8| <  5% (см. Табл. 2 и 3);

‒ для системы из 121 сферы (капель воды в воздухе), центры которых равномерно расположены в одной плоскости [37], эффекты многократного рассеяния существенны при всех рассмотренных параметрах.

На примере систем из трех сфер также показано, что существуют конфигурации, где положение сфер при одних и тех же параметрах системы практически не влияет на характер многократного рассеяния. Однако в большинстве случаев эффекты многократного рассеяния существенно зависят не только от основных параметров системы, но и от положения сфер в конфигурации.

Работа выполнена при поддержке государственного задания № 0246-2019-0052.