Численный анализ напряженно-деформированного состояния листовых рессор

Несомненным достоинством таких подходов является их аналитический характер, однако достигается это за счет существенных упрощений рассматриваемой проблемы, в частности:

• •    не выполняются реальные граничные условия в центральном сечении листовой рессоры (здесь появляются не существующие в действительности касательные усилия);

• •    не принимаются во внимание обусловливающие нелинейный характер деформирования рессорной конструкции большие перемещения листов, а контактные взаимодействия между ними рассматриваются не фактические, а гипотетические;

• •    не учитываются особенности напряженного состояния листовых рессор, вызываемые усилиями их стягивания и условиями взаимодействия с транспортным средством (ТС).

Все эти факторы устраняются при численном подходе к исследованию напряженно-деформированного состояния данных конструкций. Поэтому целью настоящей работы является построение моделей, позволяющих проводить анализ напряженного состояния листовых рессор современными численными методами с использованием надежных пакетов прикладных программ.

Полное исследование статического нагружения листовой рессоры состоит из анализа ее напряженно-деформированного состояния без заделки в ТС и в условиях заделки. В каждом из этих случаев последовательно рассматриваются сборочные напряжения и напряжения, обусловленные приложением к конструкции контрольной нагрузки.

Целью расчета является определение напряженного состояния в листах рессоры, стрелы выгиба, прогиба под действием нагрузки, жесткости, усилия стягивания листов и коэффициента использования материала К _ИМ . Параметр К _ИМ характеризует эффективность конструкции и находится из отношения энергии деформации нагруженной рессоры к энергии деформации, вычисляемой в предположении, что в каждой точке конструкции реализуется максимальное напряжение. В случае, когда листы рессоры имеют прямоугольное сечение, указанное отношение для вычисления параметра К _ИМ приобретает следующий вид:

^ j S i ( x ) c 2 ( x ) dx

• 1    i = 1 L_i

• 2.    Напряженно-деформированное состояние рессоры без заделки в ТС

К _ИМ =         _n            ,                                                          (1)

3    (∑Vi)σ2max i=1

где n — число листов рессоры; S_i ( x ) — площадь сечения i -го листа рессоры с координатой x (Рис. 1); V i — объем i -го листа; c 2 ( x ) — максимальное в произвольном сечении x значение нормального напряжения в i -м листе; σ _max — максимальное нормальное напряжение в листах рессоры.

Известные методики расчета листовых рессор [2–5] ограничиваются именно этим случаем, то есть расчетом напряженно-деформированного состояния рассматриваемой конструкции без заделки в ТС. В настоящей работе задача о расчете четвертной (тип рессоры) [4] листовой рессоры без ее заделки в ТС решается как задача с контактным взаимодействием без трения геометрически нелинейных упругих рессорных листов, находящихся в плоском напряженном состоянии.

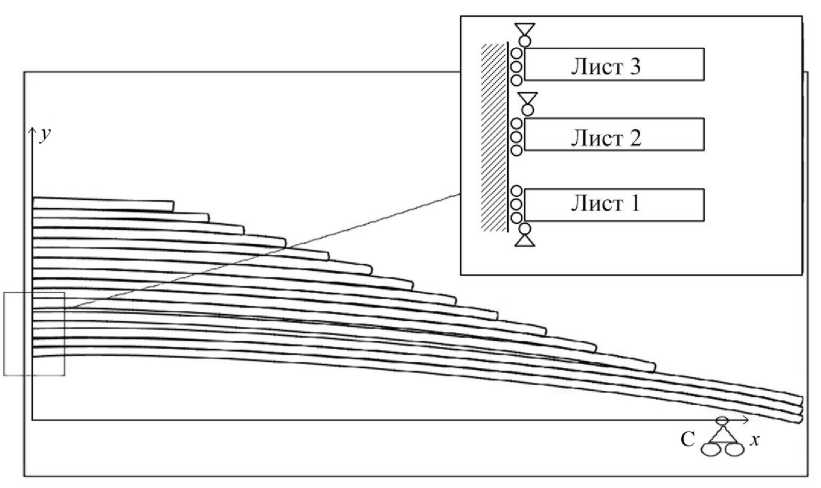
Рис. 1. Расчетная схема многолистовой рессоры без заделки

Формулируются следующие граничные условия. Для левых торцевых сечений листов (Рис. 1) выполняются условия симметрии. Однако при задании только этих условий листы рессоры оказываются не закрепленными как абсолютно твердые тела. Поэтому в дополнение к условиям симметрии фиксируются перемещения одной из точек в торцевом сечении каждого листа. В такой точке при решении задачи может возникать нарушающее условие симметрии касательное усилие. Это усилие устраняется последовательными приближениями посредством перемещения точки закрепления листа в направлении действия касательного усилия. В точке С ограничивается перемещение по вертикали 1-го листа. В естественном состоянии листы рессоры имеют заданную кривизну и своей нижней точкой правого торцевого сечения опираются на нижний смежный лист. Перемещения и углы поворота в листах не ограничиваются по величине. Напряженно-деформированное состояние рессоры на каждом шаге решения находится методом конечных элементов с использованием пакета ANSYS.

• 3.    Расчет сборочных напряжений

Под сборочными напряжениями понимаются напряжения в рессоре, обусловленные наличием заданной кривизны ее листов в естественном состоянии и возникающие вследствие стягивания листов рессоры в центральном сечении. Сборочные напряжения разыскиваются в следующей последовательности. На первом этапе лист 2 стягивается с листом 1, что достигается движением закрепленной в левом сечении точки на листе 2 в направлении листа 1. Такое действие осуществляется пошагово, и на каждом шаге решается контактная задача геометрически нелинейной теории упругости. На втором этапе к уже собранной группе листов 1 и 2 аналогичным образом подтягивается лист 3. На этом этапе контактные взаимодействия наблюдаются как между 2-м и 3-м, так и между 2-м и 1-м листами. Затем аналогично притягивается лист 4 и так далее. После сборки всех листов рессоры в точках торцевых сечений, где имеются закрепления листов, указанным выше способом устраняются нарушающие условия симметрии касательные усилия. В результате вертикальные усилия остаются только в нижней точке торцевого сечения первого листа и верхней точке торцевого сечения последнего листа. Значения этих усилий одинаковы и равняются усилию затяжки в расчете на единицу ширины листов рессоры.

Для примера рассматривается 15-листовая (многолистовая) рессора автомобиля УралАЗ. Усилие стягивания, равное 5243,6 Н, выбирается таким, чтобы расстояние между нижней поверхностью 1-го листа и верхней поверхностью 15-го листа рессоры равнялось суммарной высоте поперечных сечений ее листов в естественном состоянии. Упругое взаимодействие листов проявляется в том, что некоторые листы вминаются друг в друга, между ними возникают распределенные контактные взаимодействия (пары листов 1–2, 2–3 и так далее). Между другими парами листов наблюдаются невыбранные зазоры (пара 12–13, Рис. 2).

Нормальные сборочные напряжения на нижней стороне 3-го листа, вычисленные по различным методикам (вариант 1 — метод концевых сил; вариант 2 —метод беззазорного касания; вариант 3 — метод Таланцева Н.Ф., вариант 4 — численный расчет ANSYS), показаны на рисунке 3. По отношению к численному расчету (вариант 4) погрешность вычисления максимальных напряжений в данном листе составляет (в скобках указан номер варианта): 25,8% (1); 6% (2); 41% (3).

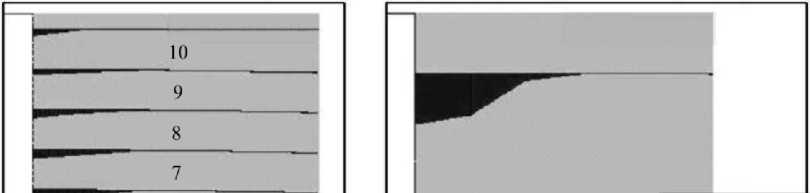
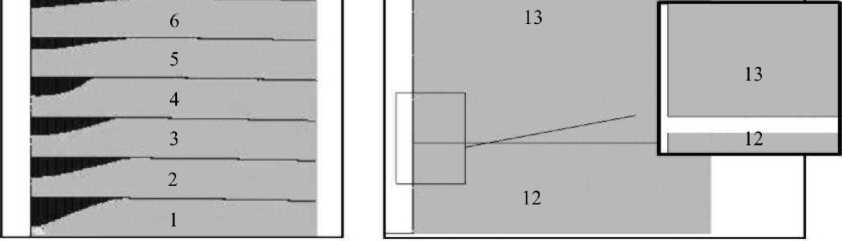
Рис. 2. Контактные усилия между листами рессоры в окрестности центрального сечения

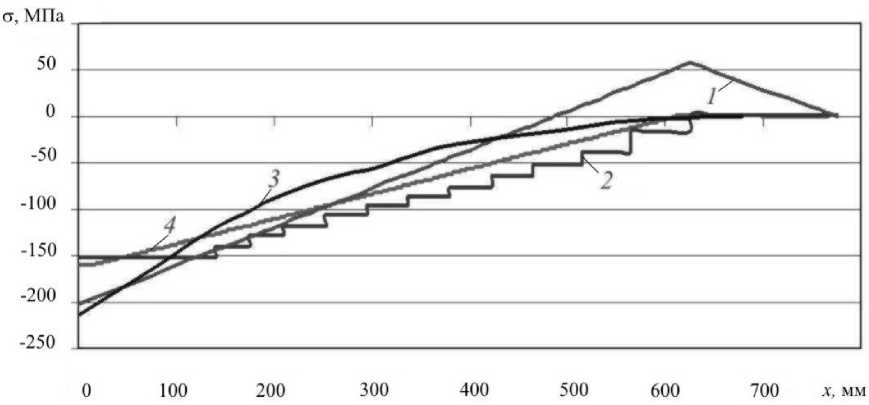
Рис. 3. Нормальные сборочные напряжения на нижней стороне 3-го листа многолистовой рессоры:

1 – метод концевых сил; 2 – метод беззазорного касания;

3 – метод Таланцева Н.Ф.; 4 – численный расчет ANSYS

Наибольшая погрешность вычисления таких напряжений в целом по рессоре оказывается следующей (в скобках указан номер листа, в котором она вычислена): вариант 1— 34,4% (1-й), вариант 2— 188% (15-й), вариант 3— 56% (1-й). Стрела выгиба собранной рессоры определяется формой 1-го листа и оказывается равной 104,6 мм.

• 4.    Расчет на внешнюю нагрузку

  Вследствие нелинейности рассматриваемой задачи принцип суперпозиции для вычисления суммарных напряжений, обусловленных и затяжкой, и внешним нагружением, оказывается неприемлемым. Поэтому расчет на внешнюю нагрузку рассматривается как следующий после сборки шаг нагружения рессоры. Предварительно нагруженная сборочными напряжениями, принявшая форму рабочей конструкции рессора нагружается кинематически в точке опоры С до состояния, отвечающего контрольной нагрузке P_k . Верхняя точка верхнего листа и нижняя точка нижнего листа в левом торцевом сечении закреплены от перемещения по вертикали. Между листами реализуется силовое взаимодействие, определяемое посредством решения контактной задачи на каждом шаге нагружения. В результате нагружения рессоры нарушается условие симметрии решения в центральном сечении: в точках закрепления листов вновь появляются касательные усилия, которые были устранены при расчете сборочных напряжений. Так же, как и в предыдущем случае, эти усилия обнуляются посредством перемещений точек их приложения. В результате вертикальные усилия в центральном сечении оказываются приложенными лишь в двух точках — в самой верхней и самой нижней. Значение нагрузки в нижней точке и является измененным усилием стягивания рессоры в центральном сечении. В рассматриваемом примере усилие стягивания рессоры изменяется до значения 2920 Н, то есть уменьшается на 44,3%. В нагруженной рессоре передача усилий между смежными листами происходит как за счет их сосредоточенных, так и распределенных составляющих.

• 5.    Напряженно-деформированное состояние листовой рессоры с заделкой

На рисунке 4 изображены контактные взаимодействия для первых четырех листов рессоры вблизи ее правого конца. Видно, что влияние друг на друга первых трех листов осуществляется в виде распределенных усилий по контактным поверхностям, а взаимодействие между 3-м и 4-м листами — практически посредством сосредоточенной силы на конце четвертого листа. Максимальные нормальные напряжения на нижней стороне листов, вычисленные по различным методикам, отличаются от напряжений, полученных по варианту 4, следующим образом: вариант 1 — 204% (3-й лист); вариант 2 — 32% (15-й лист); вариант 3 — 13% (14-й лист). При этом локализация

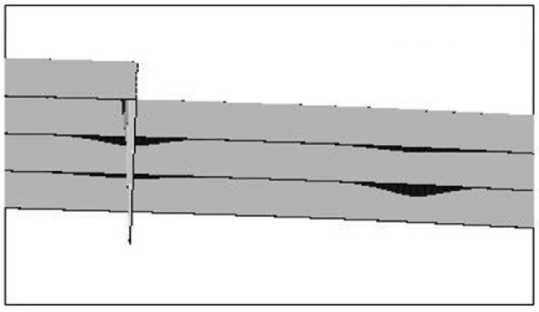
Рис. 4. Контактное давление между листами вблизи правого конца

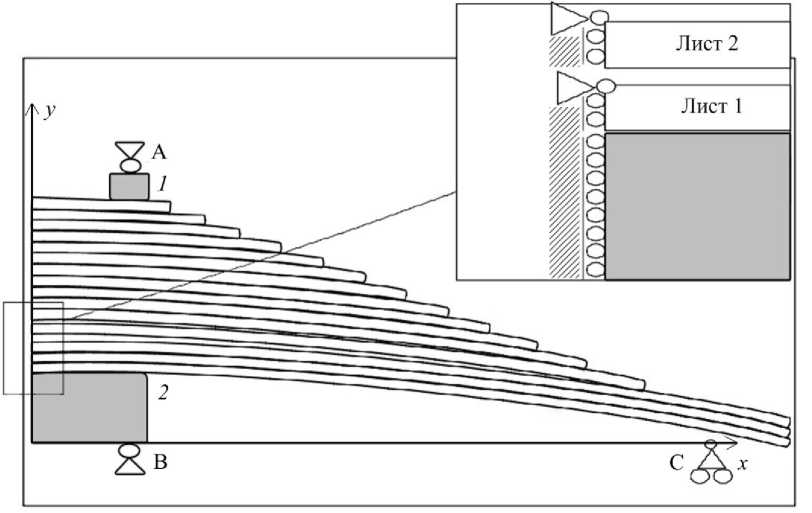
Рис. 5. Расчетная схема рессоры с заделкой в ТС сечений листов, где наблюдается максимальное напряжение, в рассматриваемых методах расчета оказывается различной, отличающейся от точек реализации таких напряжений в численном решении.

Таким образом, проведенные расчеты свидетельствуют, что допущения, использующиеся в практике расчета листовых рессор, приводят к недостаточно точному определению максимальных напряжений и недостоверному определению сечений, в которых такие напряжения наблюдаются.

При установке рессоры в ТС она стягивается усилиями, передаваемыми в точках А и В через U -образную стремянку на упругие элементы, представляющие собой массивную подушку 1 и накладки 2 (Рис. 5). Острые углы этих элементов сглаживаются. Принимаются следующие граничные условия:

• •    в центральном сечении для листов и подушки выполняются условия симметрии;

• •    в точке В подушка шарнирно опирается на горизонтальную плоскость;

• •    между листами рессоры, а также между рессорой, подушкой и накладкой допускается контактное взаимодействие без трения;

• •    в точке С рессора шарнирно опирается на горизонтальную плоскость.

• 6.    Расчет сборочных напряжений

Сформулированных условий недостаточно для того, чтобы обеспечить закрепление элементов рессоры как абсолютно твердых тел. Поэтому в центральном сечении дополнительно фиксируется перемещение по вертикали по одной точке в каждом листе. В таких точках при нагружении возникают вертикальные реакции, которые устраняются движением этих точек в направлении действия сил.

В рассматриваемом случае сборочные контактные усилия и напряжения в элементах рессоры формируются нагружением стремянки, в результате которого точка А перемещается по вертикали к точке В. При этом рессорные листы, имеющие заданную кривизну, стягиваются. В точке опоры С какая-либо реакция не возникает. Усилие стягивания стремянки ограничивается сверху пределом прочности ее стержневых элементов. От величины усилия стягивания стремянки зависят величины формирующихся в этом процессе контактных усилий и напряжений в листах рессоры.

В настоящей работе во всех приведенных примерах принимается, что усилие стягивания листов рессоры порождает напряжения в стержнях стремянки 200 МПа.

На рисунке 6 приводятся нормальные напряжения на нижней стороне с 6-го по 10-й листы рессоры, а на рисунке 7 — контактные взаимодействия между элементами рессоры. В обоих случаях рассматривается рессора с заделкой в ТС без нагружения контрольной нагрузкой P_k . Повышенные значения напряжений в листах рессоры наблюдаются лишь вблизи центрального сечения. Контактные взаимодействия локализуются в области, заключенной между подушкой и накладкой. При этом между листами рессоры эти взаимодействия проявляются в виде распределенных усилий.

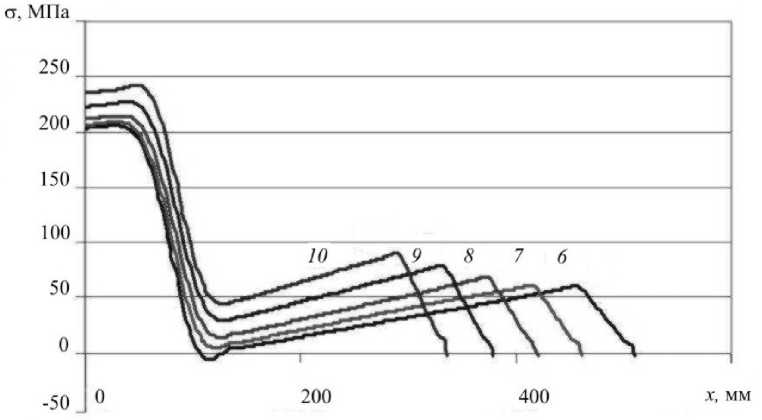
Рис. 6. Нормальные напряжения, возникающие на нижней стороне с 6-го по 10-й лист ненагруженной рессоры с заделкой в ТС

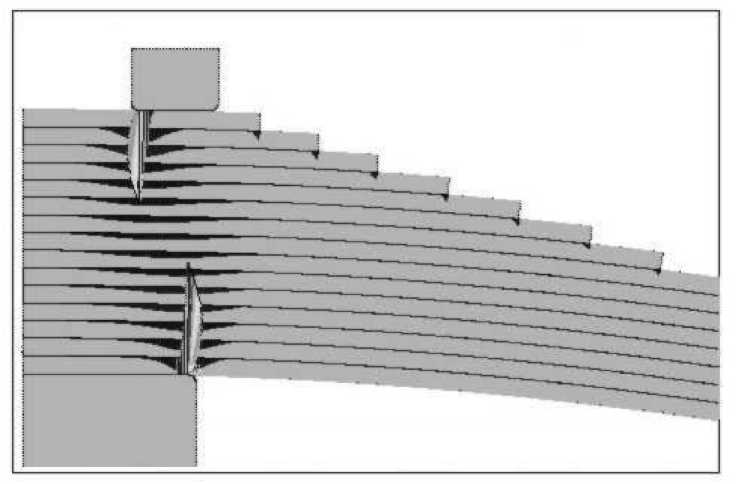
Рис. 7. Контактные усилия, возникающие при стягивании листов в ненагруженной рессоре с заделкой в ТС

• 7.    Расчет на внешнюю нагрузку

• 8.    Сравнение характеристик много- и малолистовой рессор

Рессора, стянутая стремянкой, подвергается кинематическому нагружению в точке опоры С до достижения реакцией в этой точке величины P_k . Граничные условия сохраняются те же, что и в предыдущем случае. Результаты вычислений нормальных напряжений на нижней стороне листов с номерами 6–10 представлены на рисунке 8, а контактное давление между элементами рессоры — на рисунке 9.

Следует заметить, что при рассматриваемом усилии стягивания напряжения в листах рессоры практически равномерно распределяются по всей длине листов. Это означает, что стягивание листов нагруженной рессоры не приводит к исключению из работы области, примыкающей к центральному сечению. Все листы воспринимают прикладываемую к конструкции нагрузку. Сравнение напряженного состояния нагруженной рессоры в случаях с заделкой и без заделки в ТС показывает, что при заделке в ТС уменьшение значений максимальных нормальных напряжений на нижней стороне листов достигает 24%. При этом сечения, в которых такие напряжения

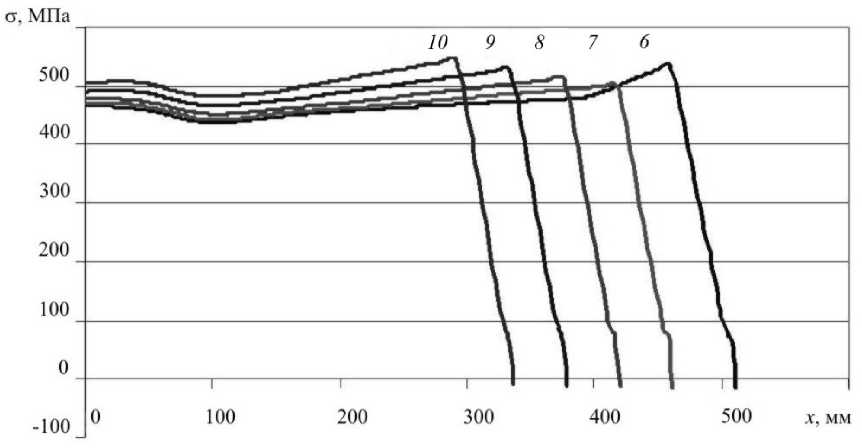
Рис. 8. Нормальные напряжения, возникающие на нижней стороне с 6-го по 10-й лист рессоры с заделкой в ТС под действием нагрузки P_k

Рис. 9. Контактное давление между листами многолистовой рессоры реализуются, оказываются различными. Контактные усилия между первыми тремя листами в нагруженной рессоре являются только распределенными. Начиная с 4-го, по концам листов действуют сосредоточенные силы, в области центрального сечения — снова распределенные. При нагружении рессоры напряжение в стержнях стремянки уменьшается на 79%. Жесткость рессоры рассчитывается как отношение приложенного к рессоре усилия к ее прогибу. При заделке в ТС жесткость рессоры увеличивается на 15,1%. Увеличение жесткости обусловливает уменьшение на 13,6% прогиба рессоры под действием контрольной нагрузки.

Предлагаемый в настоящей работе подход к исследованию напряженно-деформированного состояния листовых элементов подвески ТС является универсальным и позволяет оценить на основе принципа равномерности распределения плотности энергии деформации эффективность новых, менее материалоёмких, конструкций, имеющих аналогичные функциональные возможности. С этой целью рассматривается 5-листовая рессора переменного поперечного сечения, расчетная схема которой приведена на рисунке 10 ( 3 — прокладки между листами рессоры; здесь сохранены обозначения рисунка 5).

Методика исследования данной конструкции совпадает с приведенной выше методикой исследования многолистовой рессоры. Поэтому здесь приводятся лишь сравнительные характеристики расчетных параметров. Принципиальным отличием контактного взаимодействия между листами рассматриваемых конструкций при их нагружении в условиях заделки в ТС является то, что в многолистовой рессоре по концам отдельных листов возникают значительные по величине сосредоточенные силы (Рис. 9), а в малолистовой рессоре силового взаимодействия по концам листов рессоры не происходит. Такое взаимодействие осуществляется преимущественно посредством распределенных сил. Незначительные усилия, распределенные на коротких участках (их можно условно назвать сосредоточенными) возникают в окрестностях сопряжения образующих листов рессоры (Рис. 11).

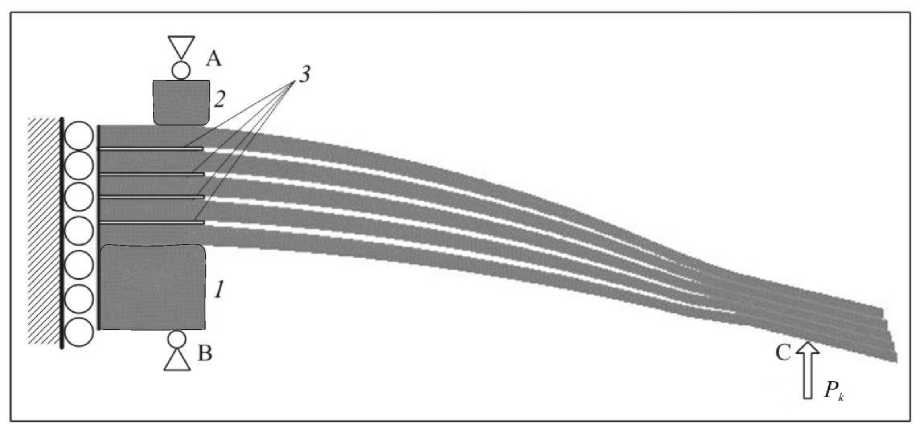
Рис. 10. Расчетная схема малолистовой рессоры при заделке в ТС

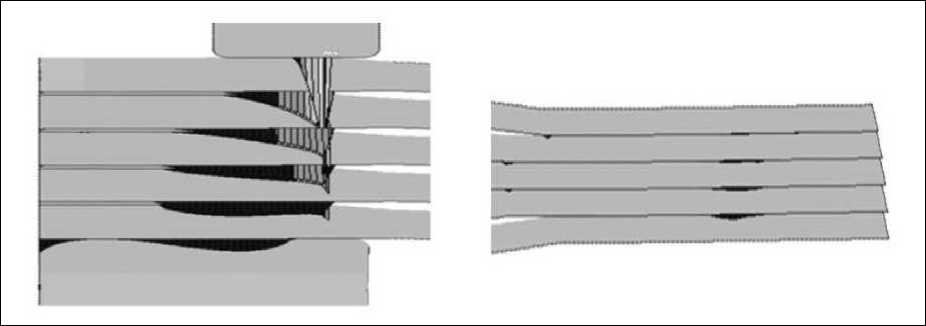
а б

Рис. 11 Контактные давления между листами малолистовой рессоры при нагрузке P_k : а – в окрестности центрального сечения; б – вблизи концов листов

В таблице 1 приводится диапазон изменения максимальных нормальных напряжений в листах многолистовой и малолистовой рессор. Видно, что малолистовая рессора нагружена более равномерно. В подобной конструкции этот факт обусловливается большим коэффициентом использования материала (см. формулу (1)). Сравнение К _ИМ для рассматриваемых рессор приводится в таблице 2. Таблица свидетельствует, что параметр К _ИМ малолистовой рессоры значительно выше (на 74%) параметра К _ИМ многолистовой рессоры. По этому параметру малолистовая рессора является более эффективной конструкцией по сравнению с многолистовой.

Параметры жесткости (отношение приложенного контрольного усилия к соответствующему прогибу) рессор сравниваются в таблице 3. Жесткости рассматриваемых рессор практически одинаковы.

Таблица 1. Изменение максимальных напряжений в листах рессоры (МПа) при заделке в ТС

Тип рессоры	Диапазон изменения
	от	до
15-листовая	369,3	755,8
5-листовая	591,8	660,9

Таблица 2. Коэффициент использования материала 3 К _ИМ

Взаимодействие с ТС	Тип рессоры
	15-листовая	5-листовая
Без заделки	0,19	0,49
С заделкой	0,31	0,54

Таблица 3. Параметры жесткости (Н/мм) рессор

Взаимодействие с ТС	Тип рессоры		Увеличение жесткости 5-листовой рессоры,%
	15-листовая	5-листовая
Без заделки	245,86	252,08	2,5
С заделкой	282,99	291,84	3,1

• 9.    Выводы

Предлагаемая в работе численная методика исследования параметров напряженно-деформированного состояния листовых рессор обладает большей универсальностью и достоверностью в отличие от используемых на практике аналитических методов. Она позволяет проводить детальное исследование конструкций в условиях без заделки в ТС и с заделкой, определять контактное взаимодействие между отдельными элементами, изучать изменения параметров конструкции в зависимости от усилий стягивания листов и прикладываемой нагрузки.