Численный анализ напряженно-деформированного состояния пряди каната c линейным касанием при растяжении и кручении

Стальной канат широко используется в современной технике, особенно в подъемнотранспортных машинах и механизмах. Существует большое количество видов канатов, но основными конструктивными факторами, определяющими форму и границы применимости того или иного вида, являются: порядок свивки, профиль поперечного сечения отдельной проволоки, форма контакта между проволоками в пряди, контакт прядей в канате.

В конструкции каната одинарной свивки проволоки с осями в форме винтовых линий свиты в один или несколько слоев вокруг центральной прямолинейной проволоки. Канаты одинарной свивки называются также спиральными канатами. Если произвести дальнейшую свивку спирального каната, получится так называемый канат двойной свивки; при этом спиральный канат будет называться прядью. Заметим, что в канатах двойной свивки центральная проволока пряди имеет форму винтовой линии. Продолжая аналогичным образам процесс свивки, можно получить канат любого порядка свивки. Наибольшее распространение получили спиральные канаты и канаты двойной свивки. При свивке проволок в пряди по слоям с разным шагом контактирование слоев проволок будет происходить в точках. Если же шаг свивки слоев проволок одинаков, то проволоки

лежащего выше слоя укладываются в углубления, образованные проволоками нижнего слоя; контакт слоев проволок в этом случае происходит по линиям. В прядях с большим количеством слоев возможна комбинация точечного и линейного контакта слоев проволок.

Проанализировав по работам [1–3] историю развития представлений о самом канате и явлениях, связанных с его работой, можно выделить несколько основных подходов к теории расчета канатов и проследить эволюцию этих подходов.

Теория гибкой нити, в которой канат отождествлялся с некоторой эквивалентной по внешним свойствам нитью без структурных особенностей, господствовала до начала 60-х годов XX-го века и сыграла в силовом расчете канатов свою прогрессивную роль, особенно в задачах динамики шахтного подъема. А.Н. Динник [1] впервые связал внешние упругие характеристики каната с его внутренней геометрией.

В работах М.Ф. Глушко [2] и его учеников было развито перспективное направление в механике канатов, обеспечивающее более высокую точность расчета и максимальную приближенность к конструкции реального каната по сравнению с теорией гибкой нити. В основу этого направления положена дискретная модель: канат представляется в виде сложной статически неопределимой стержневой системы, в общем поддающейся расчету методами строительной механики.

Альтернативным и относительно новым в механике канатов является направление, основанное на континуальном подходе, принципиально отличающееся и от дискретной модели, и от теории гибкой нити [3]. Непрерывная модель подразумевает, что канат представляет собой сплошной цилиндр с анизотропией, соответствующей моделируемой конструкции. При этом подходе точность расчетной модели (в отличие от дискретной) повышается с увеличением плотности упаковки проволок в канате, а форма поперечного сечения отдельной проволоки не имеет значения.

Отдельно стоит отметить работы [4] и [5], которые можно отнести к последним исследованиям в этой области. В [4] предложены два новых подхода, первый из которых опирается на теорию волокнистых композитов и решение задачи Сен-Венана для цилиндра с винтовой анизотропией. Второй подход базируется на решении методом конечных элементов трехмерной задачи теории упругости для сплошного неоднородного цилиндра, образованного конечным числом упругих волокон, имеющих формы винтовых линий и соединенных слабым (имеющим модуль Юнга на несколько порядков ниже модуля Юнга волокна) заполнителем. В работе [5] проведен анализ процессов фреттинг-разрушения (механического изнашивания соприкасающихся тел при колебательном относительном микросмещении), приводящего к снижению долговечности канатов.

Вне зависимости от используемых подходов связь между продольной силой T , крутящим моментом M , продольной деформацией 8 и относительным углом закручивания ф имеет следующий аналитический вид:

d ii8 + dпф = T, (1) d 128 + d 22ф = M, где d11 и d22 — обобщенные коэффициенты жесткости при растяжении и кручении; d12 — некоторый обобщенный коэффициент влияния. Отсюда следует, что:

– в общем случае продольная сила, помимо продольной деформации, порождает кручение, а крутящий момент, помимо кручения, — продольную деформацию (под общим случаем здесь понимается ситуация, когда один из концов каната закреплен, а второй полностью свободен);

– жесткости при растяжении De и кручении Dt существенно зависят от характера закрепления концов каната.

Пример 1 . Пусть канат растягивается силой T , и его концы закреплены от вращения ( ф = 0 ). Тогда, разрешив (1) относительно деформаций, получим:

T = d, ,8,    M = d, 2е,     8 = —,    M = d12 T.(2)

d11

Жесткость при растяжении в этом случае равна D e = d 11 . Такой вариант нагружения называется чистым растяжением каната. Под действием растягивающего усилия в канате возникает крутящий момент, уравновешивающийся моментом в закреплении. Очевидно, что при 8 = 1 получим: T = d 11 ; M = d ₁₂. Следовательно, коэффициент d 11 , равный силе, вызывающей единичную деформацию растяжения, есть жесткость каната при чистом растяжении.

Пример 2. Если уберем закрепление второго конца от вращения ( ф / 0 ), то канат под действием внутреннего крутящего момента будет раскручиваться. Тогда получим:

8 =

Td ₂₂

d ₁₁ d ₂₂

² d ₁₂

ф =

Td 12

d ₁₁ d ₂₂

d

Такой вид нагрузки принято называть свободным растяжением каната. Отрицательное кручение означает, что канат раскручивается относительно положительного направления свивки. В этом случае жесткость при растяжении равняется De =

d ₁₁ d ₂₂

d 1 ² 2

Пример 3. Пусть канат закручивается моментом M , а его концы закреплены от осевых перемещений ( 8 = 0):

M = d 22 Ф ,     T = d 12 Ф ,    Ф = M , T = d ¹² M .

Такой вид нагрузки принято называть чистым кручением каната. Коэффициент d ₂₂ является жесткостью каната при чистом кручении.

Из примеров следует, что коэффициент влияния d ₁₂ имеет двоякий механический смысл. При чистом растяжении ( 8 = 1, ф = 0 ) он равен крутящему моменту в канате, при чистом кручении ( 8 = 0, ф = 1 ) — осевому усилию.

Сравним математическое описание деформирования спирального каната и прямолинейного упругого сплошного изотропного стержня. Основное отличие заключается в том, что деформации стержня при растяжении и кручении описываются двумя независимыми уравнениями [2]:

T = EF 8 , M = GI p ф (5)

( E — модуль Юнга материала, F — площадь поперечного сечения, I _p — полярный момент инерции сечения стержня относительно его оси), тогда как для каната имеем систему двух уравнений (1). При этом все известные подходы элементарной теории прямолинейных изотропных стержней (метод гипотез, теория Сен-Венана, асимптотические методы теории упругости) к построению решения задачи НДС стержня дают один и тот же результат для его жесткости при растяжении: D e = d 11 = EF .

В теории канатов разные подходы приводят к различным аналитическим выражениям для жесткостей d_ij [4].

Проиллюстрируем применение подходов М.Ф. Глушко [2] и И.П. Гетмана, Ю.А. Устинова [4] к расчету обобщенных жесткостей и коэффициентов влияния. Аналитические выражения для обобщенных жесткостей и коэффициентов влияния имеют вид:

– по М.Ф. Глушко [2]

d 11	46 Г           3      , ту Т sin ai     3     , Т sin ai     2 A = L ( EF i cos a i + Ei I i    2 cos a i + G i I pi    2 cos ab                      (6) i                                      riri
d 12	42 V"1 / 7-           2      •              T cos a; • 3        7- T Z1 .      2 X cos a. • 3 X      /-7Х = > ( EFr cos a,, sin a,. + GJ. ------L sin a,.- EJ, (1 + cos a,.)------L sin a,.),   (7) iii         i       i     ipi                   i     ii              i                    i i                                                     riri
d 22	= ^ ( EiFir i^ cos a i sin 2 a i + G i I pi cos 7 a i + E i I i (1 + cos 2 a i ) 2 sin 2 a i cos a i );         (8)

– по И.П. Гетману, Ю.А. Устинову [4]

d 11 = n k 1 a ² E 1

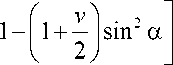
d ₁₂ = n k₁ a ³ E 1 tg a

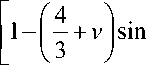
d ₂₂ = n k 1 a ⁴ E 1 tg² a —

1 f 3,3 v b 2

1 - — +--sin a

I 2 4 )

.

В выражениях (6)–(8) индекс i является идентификатором произвольной проволоки, у которой E_i — модуль упругости материала, F_i — площадь поперечного сечения, r i — расстояние между осью каната и ее центральной осью, a₄ — угол свивки, I_i — момент инерции сечения относительно ее оси; G_i — модуль сдвига материала; I_pi — полярный момент инерции.

В выражениях (9)–(11) приняты обозначения: k ₁ — параметр, который равен отношению суммарной площади поперечных сечений волокон к площади поперечного сечения каната как кругового цилиндра; a — радиус каната как кругового цилиндра; E 1 — модуль упругости материала волокон; a — угол наклона внешнего волокна к оси каната; v — коэффициент Пуассона волокон.

Достоинством перечисленных подходов является их аналитический характер. Но, чтобы получить конечные формулы, в рассматриваемой задаче приходится прибегать к ряду существенных упрощений, в частности:

• 1.    В теории академика А.Н. Динника не учитывается поперечное сужение каната и напряжения вследствие изгиба и кручения проволок. Эта теория оказалась малоэффективной при оценке прочности каната, так как не давала реальной картины распределения напряжений в поперечном сечении каната. Согласно ей напряжения в сечении распределяются равномерно, что противоречит многочисленным опытным данным анализа разрушения каната при растяжении.

• 2.    В теории М.Ф. Глушко не учитываются внутренние силы трения между элементами каната. К тому же дискретная модель не универсальна. Во-первых, потому, что размерность задачи напрямую зависит от числа проволок в пряди. Во-вторых, дискретная модель предусматривает точечный контакт элементов, составляющих конструкцию.

• 3.    Согласно теории М.Ф. Глушко полагается, что геометрически равноценные проволоки или пряди в каждом поперечном сечении каната равноценны и в силовом отношении .

• 4.    В работе [4] при анализе НДС методом конечных элементов не учитываются контактные взаимодействия между проволоками, что приводит к занижению значения жесткости d11.

2.    Общие данные об изучаемом объекте

Все эти факторы учитываются в данной работе, которая посвящается построению моделей, позволяющих проводить анализ напряженного состояния прядей каната с линейным касанием современными численными методами с использованием надежных, универсальных и высокопроизводительных пакетов прикладных программ.

Несмотря на широкое распространение современных комплексов программ конечно-элементного анализа, в отечественной литературе крайне слабо освещена проблема численного исследования НДС канатов. Близкими к данной области можно считать работы [6] и [7]. В зарубежной литературе отметим работу [8]. К сожалению, какой-либо дополнительной информации авторам получить не удалось, поэтому статья содержит некоторые описательные моменты, поясняющие материал.

Объектом исследования является прядь каната с линейным касанием двойной свивки типа ЛК-Р конструкции 6 x 19(1+6+6/6)+!.о.с. Канат 25-ГЛ-В-Л-О-Н-Т-1770 ГОСТ 2688-80 (1.о.с. означает органический сердечник). Общее количество проволок в пряди — 19 шт; шаг свивки проволок — 60 мм; диаметр пряди — 8 мм; кратность свивки — 7,5; длина пряди каната l = 100 мм; модуль упругости материала проволок E = 2∙105 МПа; коэффициент Пуассона ν = 0,3; коэффициент трения μ = 0,2. Одна из торцевых поверхностей жестко закреплена (здесь и далее под торцевой поверхностью пряди каната подразумевается совокупность торцевых поверхностей составляющих её проволок). На противоположенном торце, который свободен, моделируется поверхность с жестким поведением как наиболее точно соответствующая реальным условиям нагружения пряди каната.

Исследования распространяются на случаи статического нагружения торцевой поверхности пряди с жестким поведением. К ней поочередно прикладываются продольная растягивающая сила T (Вариант 1 ), момент M , вызывающий скручивание пряди (Вариант 2 ), комбинация силы и момента (Вариант 3 ) (Рис. 1). Условия симметрии не вводятся.

Задача расчета НДС пряди каната решается как задача контактного взаимодействия с учетом трения геометрически нелинейных проволок, находящихся в пространственном напряженном состоянии. Целью расчета является определение следующих характеристик пряди каната: продольного перемещения Δ l , интенсивности напряжений σ экв , перемещения проволок относительно друг друга (дистанции скольжения) s и контактных давлений в зонах взаимодействия проволок p . НДС пряди каната будем находить методом конечных элементов с использованием пакета ANSYS.

Для создания расчетной геометрии исследуемого объекта используется одна из распространенных в инженерной практике систем твердотельного трехмерного проектирования. На рисунке 2 показаны результаты моделирования геометрии пряди каната. В таблице 1 приведены некоторые геометрические характеристики проволок, необходимые для построения конечно-элементной модели пряди каната.

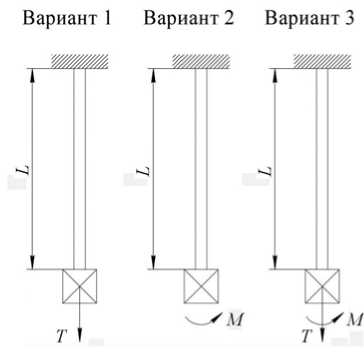
Рис. 1. Расчетные схемы нагружения

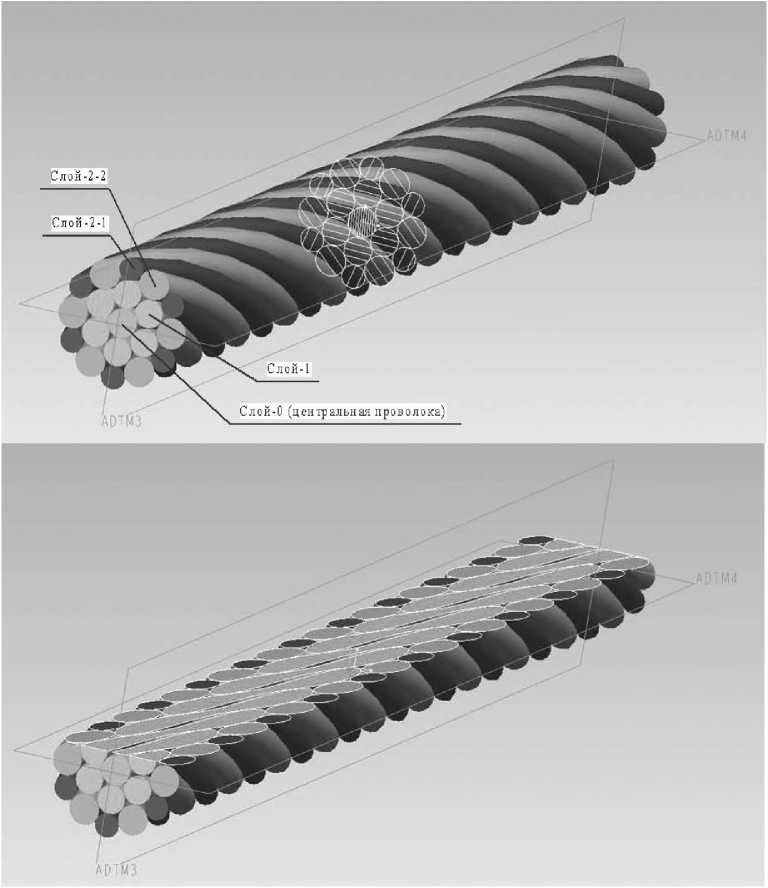
Рис. 2. Расчетная геометрия пряди каната с линейным касанием

Таблица 1. Геометрические характеристики проволок пряди каната

Номер слоя	Количество проволок, шт	Диаметры проволок, мм	Радиусы винтовых спиральных осей проволок, мм	Углы свивки, град
0	1	1,8	–	–
1	6	1,7	1,75	10,38
2–1	6	1,4	3,3	19,06
2–2	6	1,8	≈3,059	17,76

Генерация конечно-элементной сетки осуществляется посредством встроенной в ANSYS процедуры — «методом протягивания» (Sweep Method). Суть метода заключается в следующем: один из торцов проволоки выбирается «источником», второй «целью», а винтовая ось проволоки — «путем». Торец «источник» разбивается на конечные элементы (гексаэдры), которые затем «протягиваются» по «пути» до торца «цели». Данная процедура выполняется для всех проволок пряди каната. Далее определяется длина ребер конечных элементов на торцевой поверхности пряди каната. Затем для обеспечения необходимой точности расчетов и структурированности (регулярности) сетки проводится «обезразмеривание» на линиях, образующих окружности торцов всех проволок (здесь под «обезразмериванием» понимается разбиение конечных элементов на заданное количество делений по выбранной линии с целью создания более подробной сетки). Основные параметры сетки приведены в Таблице 2; полученная таким образом конечно-элементная модель пряди представлена на рисунке 3.

К основным проблемам численного анализа НДС канатов с линейным касанием следует отнести сложную структуру и множественное пространственное контактное взаимодействие между элементами каната (Рис. 4). Общее количество контактных областей (границ) в рассматриваемой пряди составляет 42. Контактные области

Таблица 2. Основные параметры конечно-элементной сетки

№ п/п	Наименование квадратичного элемента	Имя в Mechanical APDL	Количество элементов в модели пряди каната
1	20-ти узловой гексаэдр	Mesh200	11854
2	8-ми узловой контактный четырехугольник	Conta174	9996
3	8-ми узловой целевой четырехугольник	Targe170	9912

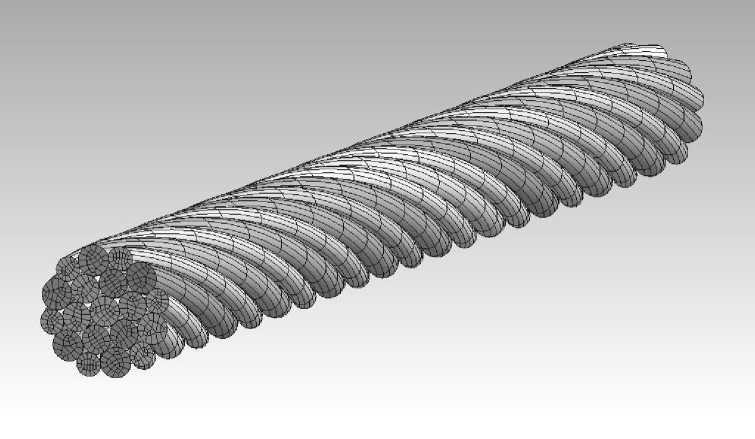
Рис. 3. Конечно-элементная модель пряди каната

Рис. 4. Контакт проволок слоя 2-1 и слоя 2-2 в пряди каната определяются следующим образом: цилиндрическая поверхность всех проволок разбивается на две полуповерхности — контактную и целевую. Следовательно, в контактах «слой 0 и слой 1», «слой 2-1 и слой 1» задействована вся цилиндрическая поверхность проволок, а в остальных случаях в контакте участвует только одна из цилиндрических полуповерхностей. При этом контакт между проволоками имеет симметричный характер.

Далее вводится команда RMODIF из пакета ANSYS, идентифицирующая параметр ICONT, задающий расстояние между точкой Гаусса контактной поверхности (точкой детектирования) и целевой поверхностью. Если указанное расстояние больше значения параметра ICONT, то контакт отсутствует (контакт со статусом «открытый»). В противном случае поверхности приходят в соприкосновение (статус контакта — «закрытый»). Введение параметра ICONT позволило снизить степень дискретизации сетки (особенно на криволинейных поверхностях).

Для математического описания контактных взаимодействий воспользуемся расширенным методом Лагранжа, который является основным алгоритмом решения подобных задач в программном комплексе ANSYS 11.0 [9]. Он базируется на итерационной процедуре метода штрафных функций. Согласно методу штрафных функций для определения контактной области между двумя поверхностями вводится понятие контактной «пружины». Жесткость такой искусственно введенной в алгоритм «пружины» называется контактной жесткостью k и является параметром штрафной функции. Если статус контакта «открытый», то есть поверхности не пришли в соприкосновение, «пружина» неактивна, при соприкосновении поверхностей она активируется и включается в алгоритм расчета. «Пружина» растягивается на величину Δ, в области контакта наступает равновесие, так как величина контактного усилия F = к А становится равной величине внешних нагрузок. Для обеспечения равновесия внешних и внутренних сил величина Δ должна быть больше нуля. В реальности проникание одной контактирующей поверхности в другую не происходит, а в ANSYS, для успешной генерации контактной пары, проникание вводится искусственно. Основные параметры контакта (контактное давление и напряжение трения) увеличиваются в процессе выполнения дополнительных итераций таким образом, чтобы конечное проникание было меньше, чем задаваемая величина допуска на внедрение. К преимуществам расширенного метода Лагранжа следует отнести то, что алгоритм на его основе минимизирует проникание одной контактной поверхности в другую, обладает меньшей чувствительностью к величине контактной жесткости, имеет лучшие условия сходимости, чем непосредственно метод штрафных функций [9].

3.    НДС пряди при различных вариантах нагружения

Рассмотрим некоторые результаты проведенного исследования. В Таблице 3 представлены данные, полученные в отдельных слоях пряди каната, а на рисунках 5–7 изображены продольные деформации и распределение интенсивности напряжений в пряди каната в целом при различных вариантах нагружения.

Таблица 3. Основные результаты расчета НДС пряди каната

Номер варианта нагружения	Нагрузка	Слои проволок	Продольные перемещения A l, мм	Интенсивность напряжений СТ экв , мПа	Контактные давления p , мПа	Дистанции скольжения s ∙10–3, мм
1	T = 1000 Н M = 0	0	0,034	58–80	0,3	1,4
		1	0,034	21–90	0,39	1,2
		2–1	0,034	12–121	4,8	1,5
		2–2	0,034	10–87	6,8	1,8
2	T = 0 M = 1 Нм	0	–0,041	70–84	0	0
		1	–0,041	14–78	0,6	0,7
		2–1	–0,041	10–97	0,5	1,2
		2–2	–0,041	5–66	7,0	1,5
3	T = 1000 Н M = 1 Нм	0	0,008	14–20	0,5	0,7
		1	0,008	12–30	0,6	1,4
		2–1	0,008	28–70	5,1	1,6
		2–2	0,008	12–33	6,8	2,1

Для оценки точности полученных результатов сравним их с результатами расчетов по методикам других авторов (см. [2], [4]). Для этого разрешим уравнения (1) относительно деформаций:

8 =

Td 22

Md 12

d 11 d 22

d

d 11 d 22

ф =

Td ₁₂

d 11 d 22

d

+

Md ₁₁

d 11 d 22

s

d

Далее по формулам (6)–(8) и (9)–(11) вычислим обобщенные коэффициенты жесткости и влияния. Учитывая, что

A l 8 =-- l

найдем продольные перемещения A l для различных

вариантов нагружения:

Td

A l =------—r l, d d-,-, d

A l =

Md

12 2 l d11 d22 - d 12

Md 12  )

d ₂₂ - d 1 ² _{2 v}

Результаты расчетов сведены в Таблицу 4.

Таблица 4. Продольные перемещения Δ l в пряди каната , вычисленные по разным методикам

Номер варианта нагружения	Нагрузка	Продольные перемещения Δ l , мм
		Методика М.Ф. Глушко [2]	Методика И.П. Гетмана, Ю.А. Устинова [4]	Решение авторов
1	T = 1000 Н M = 0	0,0340	0,077	0,034
2	T = 0 M = 1 Нм	–0,0300	–0,098	–0,041
3	T = 1000 Н M = 1 Нм	0,0048	–0,021	0,008

Из таблицы видно, что решение авторов наиболее близко к результатам по методике Глушко М.Ф., которая является в настоящее время максимально приближенной к реальной конструкции     канатов .     Значительное расхождение с результатами

И.П. Гетмана, Ю.А. Устинова объясняется достаточно большой разницей в значениях коэффициентов жесткости d ₂₂ и влияния d ₁₂ , которая, в свою очередь, образуется из-за отсутствия внутренних связей между отдельными волокнами (подробно этот вопрос освещается в работе [4]). Однако при расчете коэффициента жесткости d ₁₁ как по методикам [2] и [4], так и в решении авторов, получаются результаты с разбросом в пределах 3%. Авторам удалось получить результаты, лишь качественно совпадающие с результатами работы [3], поэтому сравнение с этим методом здесь не приводится. Отдельно стоит отметить, что методики [2] и [4] не позволяют определять дистанции скольжения.

Проанализируем поведение пряди каната в целом при разных видах нагружения.

Вариант 1.    Напряженно-деформированное    состояние пряди каната при приложении продольной растягивающей силы (Рис. 5).

Этот вид нагружения вызывает удлинение пряди каната в направлении действия силы (Рис. 5, а ), сопровождающееся раскручиванием. Интенсивность напряжений имеет неоднородный характер. Так в центральной проволоке напряжения распределяются равномерно по ее сечению, а в проволоках 2-го слоя наблюдаются минимумы напряжений, сконцентрированные в центре, и максимумы, локализованные в областях контакта со смежным слоем проволок (1-й слой) и в областях контакта проволок в самом слое (Рис. 5, б ).

Вариант 2.    Напряженно-деформированное    состояние пряди каната при приложении скручивающего момента (Рис. 6).

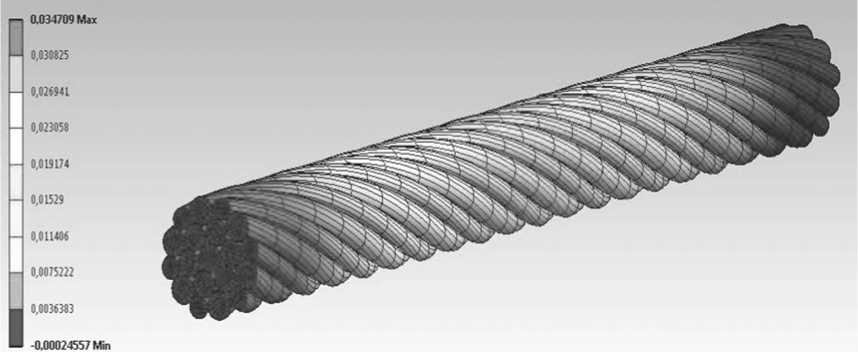
а

Рис. 5. Продольные деформации ( а ) и распределение интенсивности напряжений ( б ) при приложении к пряди каната продольной растягивающей силы

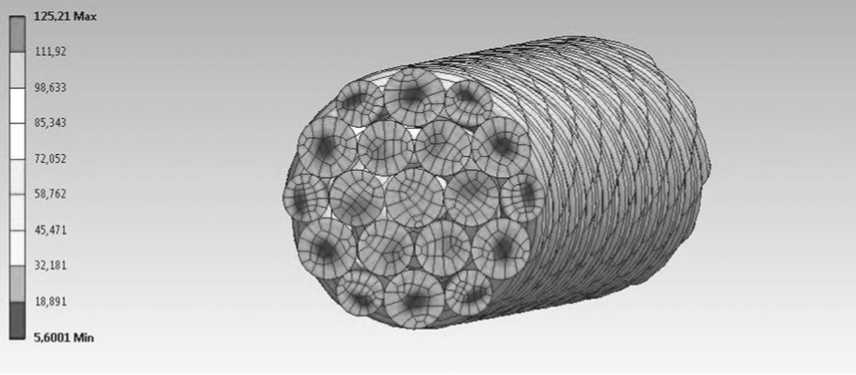
б

Рис. 5. Продолжение

а

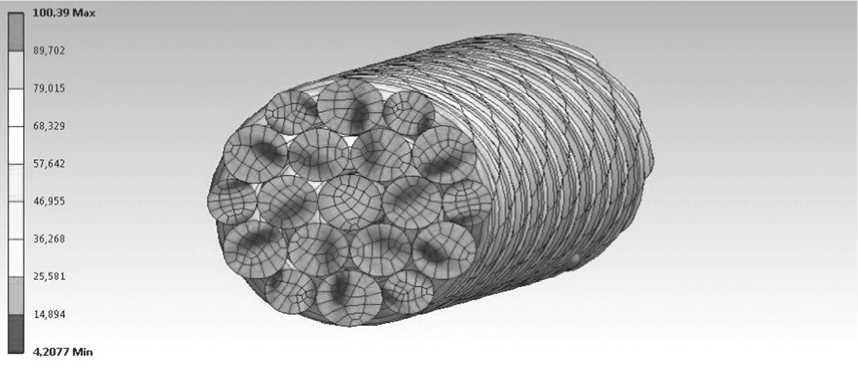
б

Рис. 6. Продольные деформации ( а ) и распределение интенсивности напряжений ( б ) при приложении к пряди каната скручивающего момента

а

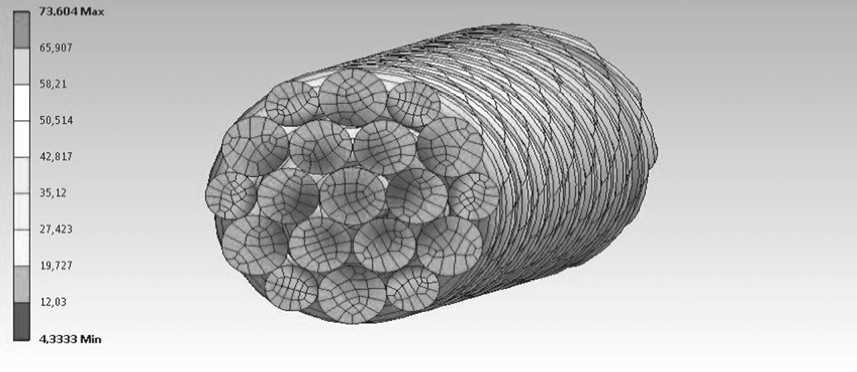
б

Рис. 7. Продольные деформации ( а ) и распределение интенсивности напряжений ( б ) при приложении к пряди каната продольной растягивающей силы и скручивающего момента

При втором варианте нагружения прядь каната скручивается, увеличиваются углы свивки проволок, происходит уплотнение пряди, сопровождающееся ее сжатием (укорочением) (Рис. 6, а ). Распределение интенсивности напряжений неравномерно (Рис. 6, б ): в центральной проволоке, вследствие ее кручения, наблюдается рост напряжений по мере приближения к ее границе; в проволоках 1-го слоя присутствуют локальные максимумы в зонах контактного взаимодействия с соседними проволоками; в наружном слое максимум интенсивности напряжений смещен в сторону контактных областей проволок самого слоя.

Вариант 3. Напряженно-деформированное состояние пряди каната при приложении продольной растягивающей силы и скручивающего момента (Рис. 7).

При комплексном нагружении абсолютное значение удлинения пряди мало по сравнению с другими вариантами нагружения, что объясняется присутствием комбинации нагрузок: растягивающая сила стремится растянуть прядь каната, а скручивающий момент, напротив, — сжать ее (Рис. 7, а ). Как и в предыдущих случаях, распределение интенсивности напряжений имеет неоднородный характер (Рис. 7, б ). Однако в центральной проволоке и проволоках 1-го слоя разброс не так велик. Слой 2–1 характеризуется наличием максимумов интенсивности напряжений в контактных областях с проволоками 1-го слоя.

Во всех трех случаях максимальные контактные напряжения наблюдаются в проволоках наружного слоя, дистанции скольжения распределяются равномерно по длине проволок (см. Таблицу 3). В работе [10] показано, что основными факторами, обуславливающими изнашивание при контактном взаимодействии, являются контактные давления и скорость скольжения. Скорость скольжения может быть определена через дистанции скольжения и время приложения нагрузки. Это позволяет научно обосновано определить закон изнашивания, то есть закон изменения размеров проволок в направлении оси, которая перпендикулярна к поверхности трения, в результате их формоизменения в процессе трения. В дальнейшем это позволит подойти к вопросу построения методов расчета канатов на долговечность.

В целом поведение смоделированной пряди каната хорошо согласуется с уравнениями (1). Наличие значительных контактных давлений и скольжения проволок относительно друг друга дает основания предполагать, что они вносят значительный вклад в работу каната в целом и требуют дальнейшего изучения.

4.    Выводы

Рассмотренная в работе методика численного анализа позволяет исследовать поведение пряди каната с линейным касанием проволок при различных вариантах нагружения, определять контактные взаимодействия между проволоками и может использоваться как вспомогательный инструмент в технических приложениях. Так на ее основе можно:

• –    дать рекомендации по использованию того или иного смазочного материала, для этого в формулировку контактного алгоритма пакета ANSYS необходимо внести величины коэффициента трения между проволоками пряди каната, полученные из экспериментов с различными смазками, рассчитать и сравнить отвечающие им НДС;

• –    более обосновано подойти к вопросам выбраковки канатов (смоделировать обрыв одной или нескольких проволок и оценить перераспределение напряжений и деформаций);

• –    рассчитать НДС канатов других, более сложных конструкций (фасоннопрядных и так называемых закрытых и полузакрытых канатов) путем создания поперечного сечения проволок отличного от кругового.