Численный анализ отражений электромагнитной волны е-поляризации от неоднородного слоя диэлектрика

В настоящее время в технике СВЧ- и оптического диапазонов широкое применение находят диэлектрические материалы, на основе которых изготавливаются такие устройства, как диэлектрические резонаторы, фазовращатели, фильтры, согласующие устройства [1–3]. Кроме того, диэлектрики в линиях передачи используются в качестве среды для передачи СВЧ-сигналов и их преобразования. Диэлектрические материалы применяются в СВЧ-технике в качестве антенных обтекателей, теплозащитных радиопрозрачных антенных окон спускаемых космических аппаратов, защитных радиопоглощающих покрытий. Диэлектрические материалы в большинстве случаев являются неоднородными. Существуют два типа неоднородных диэлектриков: среды, в которых диэлектрическая проницаемость является непрерывной функцией пространственных координат и материалы, состоящие из разделенных резкими границами однородных частей, каждая из которых обладает свои значением диэлектрической проницаемости. На сегодняшний день остается актуальным вопрос о взаимодействии электромагнитной волны со слоистыми неоднородными структурами [4–7].

С другой стороны, в настоящее время в СВЧ-и оптическом диапазонах значительный интерес представляет исследование метаматериалов, обладающих нетипичными для естественных сред электромагнитными свойствами [8—12]. Неоднородные диэлектрические слои могут использоваться как составная часть метаматериала.

К сожалению, строгие решения задачи отражения электромагнитных волн от неоднородного слоя диэлектрика конечной толщины с вещественной диэлектрической проницаемостью известно лишь для нескольких случаев. В данной статье приведен вариант численного решения задачи для монотонных профилей диэлектрической проницаемости: линейного и параболического. Для нахождения решения использовалось дифференциальное уравнение для коэффициента отражения волны Е-поляризации, полученное методом дифференциальной прогонки.

1. Наклонное падение электромагнитной волны с Е-поляризацией на неоднородный диэлектрический слой

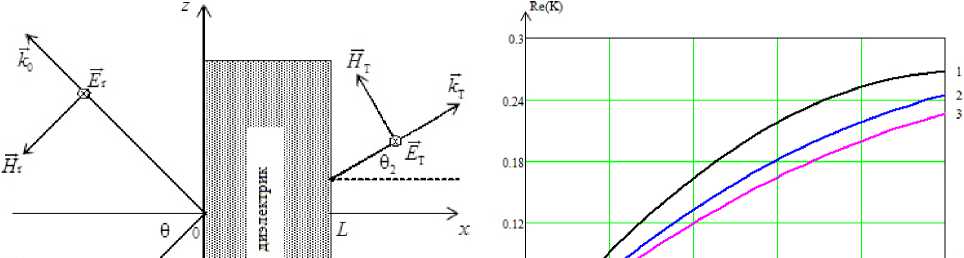
Рассмотрим электродинамическую систему (рис. 1). В области 1 (вакуума) на границу слоя под углом 9 падает плоская волна с Е-поляризацией с векторами напряженности электрического Ё _s = { о, E _s у , о } и магнитного

H s = { - H s x , 0, H sz } полей. Составляющие векторов напряженностей поля падающей волны описываемыми следующими выражениями:

Hsx (x, z, t) = - — sin 9 x x           Z0

x exp [ j ( to t + k_ti x cos 9 + k ₀ z sin 9 ) ];

Hsz (x, z, t) = — cos 9 x z          Z0

x exp [ j ( to t + k ₀ x cos 9 + k ₀ z sin 9 ) ];

ESy (x,z, t) = E0 x x exp [ j (tot + ky x cos 9 + ky z sin 9)],

где E ₀ – амплитуда напряженности электрического поля падающей волны; k y = to/ c — волновое число для плоской электромагнитной волны в вакууме; to — круговая частота; c — скорость света; Z 0 = Д Ц 0 /ед — характеристическое сопротивление вакуума; j = V-1 — мнимая единица;

Б 0 и Ц у — относительные диэлектрическая и магнитная проницаемости вакуума.

Кроме падающей волны в области 1, в общем случае существует также отраженная волна, выражения для составляющих векторов напряженностей электрического и магнитного полей имеют вид:

Hr ж (x, z, t) = - ~ Re sin 9 x x            Z0 e x exp [j (tot - kyx cos 9 + kyz sin 9)];

HRz (x, z, t) = - — Re cos 9 x z             Z0 e x exp [j (tot - kyx cos 9 + kyz sin 9)];

ERy (x, z, t) = E0 Re x x exp [j (tot - kyx cos 9 + kyz sin 9)],

где R _e – коэффициент отражения (по полю) для случая падения волны Е-поляризации.

HTx (x, z, t) = - — Te sin 9 x x            Z2 e

x exp | j (tot + k2 {x - L} cos 92 + k2 z sin 92)]; HTz (x, z, t) = — Te cos 9 x z           Z2 e x exp | j (tot + k2 {x - L} cos 92 + k2 z sin 92)]; (3) E t y (x, z, t ) = E 0 Te x x exp | j (tot + k2 {x - L} cos 92 + k2 z sin 92)], где Te – коэффициент прохождения (по полю) для случая падения волны Е-поляризации

Z 2 = V^ 2/^e2 — характеристическое сопротивление области 2; L – толщина диэлектрического поля; k 2 = k y Д Б 2 Ц 2 — волновое число для плоской электромагнитной волны в области 2; Б 2 и

Ц 2 — относительные диэлектрическая и магнитная проницаемости области 2, соответственно.

Выражения (1)–(3) определяют электромагнитные поля в областях 1 и 2.

В неоднородном диэлектрическом слое пространственные зависимости y-составляющей на- пряженности электрического поля и z-составляющей напряженности магнитного поля в предпо- ложении отсутствия зависимости векторов от координаты y и при гармонической зависимости от координаты z, описываются двумя уравнениями Максвелла в дифференциальной форме, которые для гармонических полей с временной зависимостью exp (jtot) имеют вид:

d E y

= - j toЦ o H z ; d x

d H_z d x

- jtoБo I б (x) - sin2 9 I Ey, где функция б (x) задает профиль вещественной части относительной диэлектрической проницаемости слоя.

Введем в выражениях (4) нормированные параметры:

U e (9 = ^ Д                      (5)

E ₀

– нормированная напряженность электрического поля;

V e Ю = ^Л'                   (6)

E ₀

– нормированная напряженность магнитного поля.

В выражениях (5) и (6): Г = x/L - нормированная координата.

С использованием нормировочных соотношений (5) и (6) дифференциальные уравнения (4) можно записать следующим образом:

Д|Д = - jKV e ( Г ) ;

dr                                                 (7)

d V e^ = - jK Гб ( r ) - sin² e] U e ( r ) ,

dr          L             ]

где K = k 0 L — волновое число, нормированное на толщину слоя.

Для компактной записи уравнений (7) введем следующие обозначения:

a ^{( e )} ( 6 ) —-j k ;

•<’ ( 6 ) —-j K [s ( 6 ) - sin² 0].

С учетом этих соотношений (8) уравнения Максвелла (7) в нормированном виде можно представить как d ) = A'/'(-) V (6);

d ⁶                                               (9)

" — A ^) U e ( 4 ) .

d6

Определим граничные условия для системы уравнений (9), исходя из непрерывности тангенциальных составляющих напряженностей электрического и магнитного полей на границе раздела двух сред:

E s y ( x — 0 ) + E r y ( x — 0 ) — E y ( x — 0 ) ;

H s _г ( x — 0 ) + H Rz ( x — 0 ) = H z ( x — 0 ) ;

E t y ( x — L ) — E y ( x — L ) ;

H _T z ( x — L ) = H _z ( x — L ) .

= A 2 e ) ( 6 ) U e ( 6 ) .

Используя соотношения (9) и (14), получаем следующее дифференциальное уравнение:

dO-^ —-a e ( 6 ) A ⁽ e ) ( 6 ) + a 2 e ) ( 6 ) .           (15)

d6

Очевидно, что V _e ( 0 ) — a_e ( 0 ) U_e ( 0 ) . С учетом граничных условий (12) получаем:

( 1 - R_e ) cos 0 = a_e ( 0 )( 1 + R_e ) .                  (16)

Коэффициент отражения в случае падения плоской электромагнитной волны Е-поляризации можно определить как r cos 0 - ae (0)

^e cos 0 + a_e ( 0 )

Соотношение (17) можно применять и для ча- стичного коэффициента отражения:

R e ( 6 ) =

cos 0 - a_e ( 6 ) cos 0 + a_e ( 6 )

Найдем производную по нормированной координате 6 в выражении (18):

Подставляя в граничные условия (10) выраже-

ния для составляющих векторов напряженностей электрического и магнитного полей (1)–(3),

d R_e ( 6) _        2 cos 0      da_e ( 6 )

------ —----- d⁶       [cos 0 + a_e ( 6 ) ]    d⁶

получаем:

E y ( 0 ) — E 0 ( 1 + R e ) ;

H ( 0 ) = E 0 ( 1 - R ) cos 0;                      (11)

• ^z       Z 0        ^e

E y ( L ) = E 0 T e ; H z ( L ) = E ⁰ T e cos 0.

Z ₂

Из выражения (18) следует, что коэффициент a_e ( 6 ) определяется через частичные коэффициенты отражения:

a_e ( 6 ) — cos 0

1 - R e ( 6 )

1 + R e ( 6 ) .

С учетом (5) и (6) запишем граничные условия (11) в нормированном виде:

U e ( 0 ) — 1 + R e ; V e ( 0 ) = ( 1 - R e ) cos 0;

U e ( 1 ) — T e ; V e ( 1 ) = -° T e cos 0.

Z ₂

Система уравнений (9) и граничные условия (12) составляют двухточечную граничную задачу.

• 2.    Дифференциальное уравнение для коэффициента отражения в случае падения волны Е-поляризации

Будем считать, что в общем виде:

V e ( 6 ) — a e ( 6 ) U e ( 4 ) •                             (13)

Находя производную в формуле (13) и с использованием второго соотношения из системы (9), получаем:

Из соотношений (19) и (20) получаем дифференциальное уравнение для частичного коэффициента отражения в случае падения волны Е-поляризации:

dR-^- — -^— (Aje) (6) cos2 0 [1 - Re (6)]2 - d6      2 cos 0( 1             L e ]    (21)

- A 2 ^{e )}( 6 ) [1 + ^R e ( 6 ) ] 2 } .

Интегрируя уравнение (21) по координате 6, можно получить значение коэффициента отражения в любом сечении неоднородного диэлектрического слоя. При интегрировании достаточно только задать начальное условие R_e ( 1 ) .

Для нахождения R_e ( 1 ) воспользуемся уравнением (18) и после некоторых преобразований

получим следующее соотношение для задания

начального условия:

doe_ ( 6 ) d6

d U e ( 6 ) d6

R (1)= cos 0-ae (1)

^e cos 0 + a e ( 1 )

^— 2 ^{- Z} 0

Z 2 ⁺ Z 0

В случае, когда область 1 на рис. 1 представляет собой диэлектрик с материальными пара-

Hs /

Рис. 1. Геометрия задачи: наклонное падение плоской электромагнитной волны Е-поляризации на диэлектрический слой

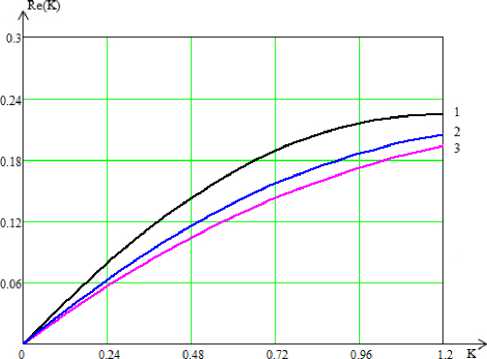
Рис. 2. Частотные характеристики модуля коэффициента отражения электромагнитной волны Е-поляризации при нормальном падении для однородного (1), линейного (2) и параболического (3) профилей диэлектрической проницаемости метрами Si и Ц1, то в выражении (22) необходимо провести замену: Zo ^ Z1 = ^Ц1 /si .

• 3.    Результаты расчетов

Представим результаты численного расчета модулей коэффициентов отражения от слоев диэлектрика с различными профилями изменения вещественной части комплексной диэлектрической проницаемости при наклонном падении электромагнитной волны Е-поляризации. Проведены вычисления при различных углах падения электромагнитной волны. При моделировании использовались следующие профили распределения диэлектрической проницаемости слоя вдоль нормированной координаты £:

• —    однородный слой с s ( ^ ) = Sl;

• —    линейный слой с s ( £ } = s L ( 1 - |1 - 2^| ) - j s L ;

006 Z/z

О          024        04S        022        096         1.2 К^

Рис. 3. Частотные характеристики модуля коэффициента отражения электромагнитной волны Е-поляризации при угле падения 30 ° для однородного (1), линейного (2) и параболического (3) профилей диэлектрической проницаемости

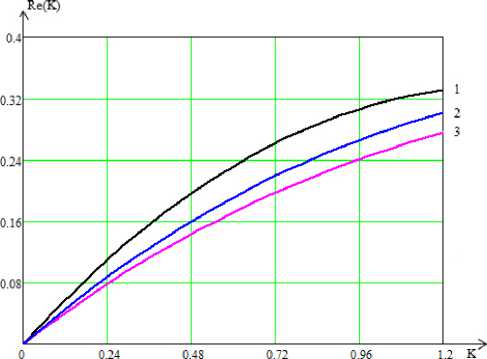
Рис. 4. Частотные характеристики модуля коэффициента отражения электромагнитной волны Е-поляризации при угле падения 45 ° для однородного (1), линейного (2) и параболического (3) профилей диэлектрической проницаемости

• —    параболический слой с е ( ^ ) = 4sL^ ( 1 - ^ ) - j s L , где ^S L = ^S L ^- j ^S L .

При расчете значение относительной комплексной диэлектрической проницаемости диэлектрического слоя выбиралось следующим: Sl = 1.5 - 0.5j.

На рис. 2–4 представлены результаты расчетов частотных характеристик модулей коэффициентов отражения от диэлектрического слоя с однородным (кривая 1), линейным (кривая 2) и параболическим (кривая 3) профилями вещественной части комплексной диэлектрической проницаемости при нормальном (рис. 2), наклонном под углами 30° (рис. 3) и 45° (рис. 4) падениях плоской электромагнитной волны Е-поляризации. Видно, что отражения от параболического профиля меньше, чем от линейного и однородного. На рис. 5 и 6. представлены

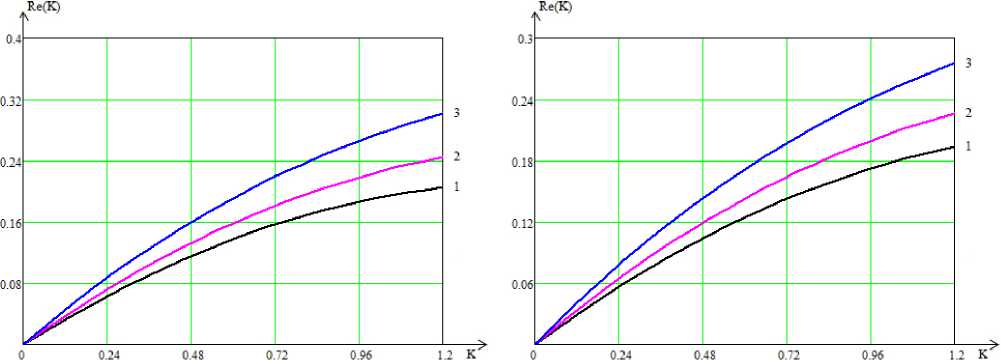
Рис. 5. Частотные характеристики модуля коэффициента отражения электромагнитной волны Е-поляризации линейного профиля диэлектрической проницаемости при нормальном падении (1) и углах падения 30 ° (2) и 45 ° (3)

частотные характеристики модулей коэффициентов отражения от слоя диэлектрика с линейным и параболическим профилями изменениями диэлектрической проницаемости при различных углах падения электромагнитной волны. Видно, что при возрастании угла падения отражения становятся больше.

Заключение

Проведено численное моделирование взаимодействия электромагнитной волны линейной поляризации с неоднородными диэлектрическими слоями. На основе дифференциального уравнения для частичного коэффициента отражения от слоя неоднородного диэлектрика рассчитаны модули коэффициентов отражения. Показано, что диэлектрики с неоднородным профилем проницаемости обеспечивают меньшие отражения. Это обстоятельство делает возможным использовать их при проектировании малоотражающих покрытий. Также, полученные в работе результаты могут найти широкое применение в области диагностики параметров СВЧ-диэлектриков, в частности степени их неоднородности.