Численный анализ процессов сложного пластического деформирования конструкционных сталей при малоцикловом нагружении

Многолетние экспериментальные и теоретические исследования накопления усталостных повреждений в конструкционных материалах позволяют сделать вывод о том, что усталость охватывает три значительно отличающиеся друг от друга области циклического нагружения [1-3]:

– многоцикловая усталость (МнЦУ) при квазиупругой работе материала (пластические деформации в пределах допуска 0,002) соответствует долговечностям при симметричном циклическом одноосном нагружении до 105–108 циклов и выше;

– малоцикловая усталость (МЦУ) при нестационарном упругопластическом деформировании материала соответствует долговечностям при симметричном циклическом одноосном нагружении до числа циклов, меньшего 10–4;

– оба механизма действуют одновременно в переходной области, соответствующей долговечностям до 104–105 циклов.

Отличить малоцикловую усталость от многоцикловой позволяет макроскопическая пластическая деформация.

Экспериментальные исследования [4–11] упругопластического деформирования металлов (в основном нержавеющих сталей) при непропорциональном циклическом нагружении показали, что изотропное упрочнение значительно превышает упрочнение при пропорциональном циклическом нагружении. Это явление было названо эффектом «дополнительного упрочнения» или «локального дополнительного упрочнения» [4, 12]. Эффект дополнительного упрочнения зависит от вида траектории циклического непропорционального нагружения. Из экспериментов также получено, что наибольшим дополнительным упрочнением обладает непропорциональное нагружение по траектории в виде окружности [4–11]. Очевидно, что отмеченный эффект дополнительного упрочнения при циклическом непропорциональном деформировании необходимо учитывать в прочностных расчётах конструкций при сложном нагружении.

В [13, 14] развита математическая модель термопластичности с кинематическим и изотропным упрочнением, описывающая процессы сложного пластического деформирования конструкционных материалов (металлов и их сплавов) при монотонных и циклических, пропорциональных и непропорциональных, режимах термосилового нагружения. В обозначениях, принятых в этих работах, для изменения радиуса С_р поверхности текучести F _p при изотропном упрочнении с учетом разделения процессов монотонного и циклического нагружения принимается следующая структура уравнения:

С р = [ q х Н ( F p ) + a ( Q s - C р ) Г ( F p )] X + q 3 Т ,

t

С p = ср + J С* pdt , 0

ij eij

( 2

2pp х I g eij eij

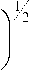
tt

X m = J x H ⁽ F ) dt ,    X = j ^X dt ,         ⁽²⁾

= q 2 А У 1 ^{+ (1 -} А) Q i q ^X      A у 1 + (1 - A )  ’

Q s

q 2 А у 2 + (1 - А ) Q i A у ₂ + (1 - A)

(0 <у , < 1, i = 1,2),     (3)

		е
A = 1 - cos2 0 ,	cos 0 = и ® и 2 ,	е               ij
		n j     , , К
		( e j e j г

n i^sj

S ij ( S ij S ij )¹²

,

Н ( F p ) =

'1, F p = 0 лр j p j > 0

0, F p < 0 vp p j < 0

I                        i j

Г ( F p ) = 1 - Н ( F p ).

Здесь q ₁ , q ₂ , q ₃ — модули изотропного упрочнения; Q ₁ и Q ₂ — модули циклического изотропного упрочнения; a — постоянная, определяющая скорость процесса стабилизации петли гистерезиса; Q_s — значение радиуса поверхности текучести в стабилизированном состоянии при данных p _max и T ( p _max — максимальный за историю нагружения модуль переменной p j ); Cр 0 — начальное значение Ср .

В уравнении (1) первый член описывает изотропное упрочнение в результате монотонного пластического деформирования (Н(Fp) = 1 и Г(Fp) = 0), второй член — циклическое упрочнение материала (Н(Fp) = 0 и Г(Fp)=1), а третий — изменение радиуса поверхности текучести при изменении температуры.

Модуль изотропного упрочнения q _х учитывает изменение изотропного упрочнения материала в зависимости от направления деформирования в данной точке траектории — угла О между вектором приращения девиатора деформаций, имеющим направляющие косинусы n_i^е_j , и нормалью к поверхности текучести в точке, определяемой направляющими косинусами nS . При пропорциональном нагружении выполняются условия: угол О = 0 ; параметр A = 0 ; q _х = q ₁, где q₁ — модуль изотропного упрочнения материала (одноосное растяжение материала. Непропорциональному нагружению отвечают условия: О = п/ 2; A = 1; q _х = q ₂, где q ₂ — модуль упрочнения при нагружении по касательной к поверхности текучести («нейтральное» нагружение). Для циклического изотропного упрочнения при циклическом пропорциональном нагружении в (1)-(5) аналогично полагается О = 0 и Qs = Q₁, а при циклическом непропорциональном нагружении — О = п/2 и Q_s = Q 2 . Коэффициенты тарирования (весовые коэффициенты) у ₁ и у ₂ являются параметрами, позволяющими корректировать влияние модулей q ₁ , q ₂ , Q ₁ , Q ₂ на изотропное упрочнение материала. При стационарном циклическом деформировании материала с постоянной амплитудой деформации и Т = const радиус поверхности текучести Cp стремится к Q s = const, и параметры петли гистерезиса стремятся к своему стабилизированному значению, определяемому величиной Qs , зависящей от текущих значений T и p max .

Далее проводится оценка применимости развитых определяющих соотношений термопластичности [13, 14] путём сопоставления вычисленных на их основе результатов исследования процессов циклического пластического деформирования конструкционных сталей при малоцикловом нагружении с имеющимися в литературе экспериментальными данными и численными результатами других авторов.

2.    Сравнение численных результатов с экспериментальными данными

В работах [9–11] приведены результаты экспериментальных исследований пропорционального и непропорционального циклического упругопластического деформирования конструкционных материалов (металлов и их сплавов), которые были получены в лаборатории механических испытаний кафедры сопротивления материалов, теории упругости и пластичности Тверского государственного технического университета на автоматизированном расчетно-экспериментальном комплексе СН-ЭВМ под общим руководством профессора В.Г. Зубчанинова. Эксперименты выполнялись при нормальной температуре T = 20 ° C на тонкостенных цилиндрических образцах с длиной рабочей части l = 100 мм, толщиной стенки h = 1 мм и радиусом срединной поверхности R = 15,5 мм, изготовленных из стали 45.

По заданной программе испытаний образцы нагружались осевой силой P , внутренним давлением интенсивности q и крутящим моментом М . Компоненты тензоров напряжений и деформаций в рабочей части образца вычислялись по формулам:

о_п = Р /( 2 п Rh ) ,    g ₂₂ = qR/h ,    о ₁₂ = M Д 2 п R ² h ) ,     о ₃₃ = а ₁₃ =о ₂₃ = 0 ,

е11 = Aljl,    е22 = AR/R ,    е12 = фR/(2l), где ф — угол закручивания.

В опытах измерялись деформации e₁₁, e ₂₂, e ₁₂ и напряжения а_п, а ₂₂, а ₁₂. Векторы напряжений σ и деформаций ε в трёхмерном совмещённом векторном подпространстве девиаторов с общим неподвижным репером { e k } имели вид:

° = Sk e k ,        e = Эк е k      ( k = 1,2,3 ) .

Компоненты S_k , Э_k векторов напряжений а и деформаций e и их модули с и е вычислялись по формулам:

S 1 = лЫ^с 11 ^-с о

— 2 ^(с 22 ^+с 33

) ’   S 2 = ^ ^(с 22 + ^С 33 ) ,   S 3 = V2^C 12 ,

Э 1 = V 2 ⁽ еи е о ) , с = V S 1 ² + S ₂ ² + S ₃² ,

сп

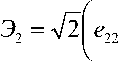
+— е,, 2 11

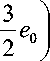
Э₃ = V2 е ₁₂,

е = V Э 1 ² + Э ₂ ² + Э ₃²,

где e о = 3 ^{( e} 11 ⁺ e 22 ⁺ e 33 ) , ^с о = ^{1 (с} 11 ^{+ с} 22 ^{+ с} 33 ) .

При обработке экспериментальных данных принималось условие несжимаемости e 11 + e ₂₂ + ^е ₃₃ = 0 и считалось, что с ₃₃ = 0 [9-11]. Эксперименты выполнялись по схеме «жесткого нагружения». В качестве траекторий сложного нагружения рассматривались траектории постоянной кривизны в плоскости Э 1 - Э ₃ девиаторного пространства деформаций А.А. Ильюшина [10, 11].

При численном моделировании экспериментальных результатов с использованием развитых определяющих соотношений упругопластичности [9, 10] заданными являлись экспериментальные траектории деформаций (закономерности изменения компонент тензора деформации ejj ( t ) ), а траектории напряжений находились путем интегрирования определяющих соотношений термопластичности по заданной истории изменения e_ij . Полученные численные результаты сопоставлялись с экспериментальными данными.

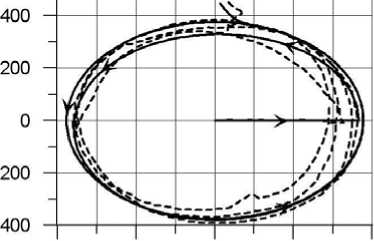
На рисунке 1 (см. легенду) представлена программа деформирования, по которой производились эксперимент и теоретический расчет тонкостенного трубчатого образца из стали 45 [9]. Трубчатый образец закручивали за предел текучести до значения Э ₃ = 0,012. После излома траектории деформирования на 90° процесс осуществлялся по окружности радиуса R = £ = 0,125. По завершению 4-х витков деформирование продолжалось по прямолинейному участку, параллельному оси деформации Э ₁ . Особенностью программы являлось то, что на траектории в виде окружности модуль вектора деформации оставался постоянным.

Расчёт процессов деформирования лабораторных образцов с использованием модели термопластичности [9] проводился при следующих материальных параметрах стали 45: модуль сдвига G = 76920 МПа; модуль объёмного сжатия K = 166670 МПа; начальный радиус поверхности текучести С^ = 340 МПа; модули анизотропного упрочнения g 1 = 8000 МПа, g ₂ = 80 (ввиду отсутствия надежных экспериментальных данных для стали 45 моделировалось только кинематическое упрочнение).

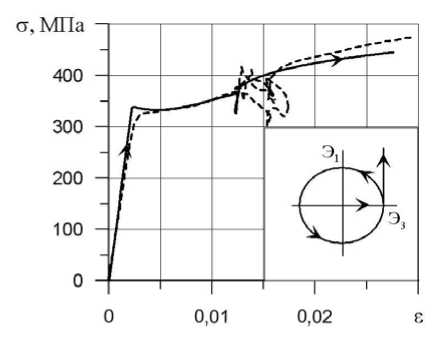
На рисунке 1 также приведены скалярные свойства материала — диаграмма сложного деформирования. Сплошной линией обозначены численные результаты, полученные авторами, а пунктирной — опытные данные [9]. Видно качественное и количественное совпадение опытных и модельных представлений.

На рисунке 2 показан отклик в пространстве напряжений S 1 - S ₃ на реализованную программу сложного деформирования, а на рисунке 3 — локальные диаграммы деформирования S 1 - Э 1 и S ₃ - Э ₃.

S„ МПа

Рис. 1. Диаграмма сложного деформирования предварительно закрученного образца при малоцикловом

-400 -200 0 200 Sp МПа

нагружении

S',, МПа

О

-200

-400

-0,02 -0,01    0    0,01   0,02 Э,

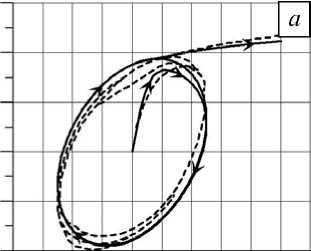
Рис. 2. Траектория напряжений на плоскости S 1 - S 3 , соответствующая реализованной плоской замкнутой циклической круговой траектории деформирования

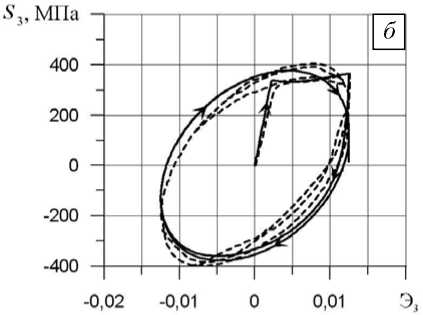
Рис. 3. Локальные диаграммы деформирования образца в координатах S 1 -Э 1 ( а ) и S 3 -Э 3 ( б )

В целом для выбранной сложной программы малоциклового нагружения расчеты и эксперимент качественно и количественно соответствуют друг другу и показывают, что используемая модель пластического деформирования материала [13, 14] приемлема для инженерных расчетов.

Следующий пример содержит результаты исследования пропорционального и непропорционального циклического упругопластического деформирования цилиндрических образцов, выполненных из стали 304 — аналога отечественных нержавеющих сталей, при нагружении осевой силой и крутящим моментом [2]. Программа испытаний была составлена таким образом, что любая комбинация линейных сегментов в пространстве деформаций e 11 - e 1 ₂ (жесткое нагружение) могла, вследствие ее непрерывности, задать цикл нагружения. Блок нагружения задавался как произвольный набор одинаковых циклов . Кроме того программа испытаний позволяла устанавливать любое число блоков, каждый из которых имел свой циклический путь нагружения. Обобщенные результаты трех типов экспериментов, включающие последовательность конечных значений регистрируемых осевых ( e ₁₁ ) и сдвиговых ( e ₁₂ ) деформаций каждого блока в пределах конкретного вида нагружения, представлены в таблице.

Расчётный анализ процессов деформирования лабораторных образцов с использованием определяющих соотношений модели пластичности с кинематическим и изотропным упрочнением [13, 14] проводился при следующих материальных параметрах стали 304: модуль сдвига G = 78700 МПа; K = 172920 МПа; C 0 = 285 МПа; g 1 = 23236 МПа, g 2 = 358,6 (ввиду отсутствия надежных экспериментальных данных для стали 304 моделировалось только кинематическое упрочнение).

Таблица. Процессы сложного деформирования при малоцикловом нагружении

Тип экспе-риме-нта	Номер блока
	Блок 1	Блок 2	Блок 3	Блок 4
A	Конечная точка последовательности:	Конечная точка последовательности:	Конечная точка последовательности:
	1. е 11 = е 12 =0	1. е 11 = е 12 =0	1. е 11 = е 12 =0
	2. е 11 =0,0041; е 12 =0,003	2. е 11 =0,0041; е 12 = – 0,003	2. е 11 =0,0041; е 12 =0,003
	3. е 11 =-0,0041; е 12 = – 0,003	3. е 11 = – 0,0041; е 12 =0,003	3. е 11 =0,0041; е 12 = – 0,003
	4. возврат к п. 1	4. возврат к п.1	4. е 11 = – 0,0041; е 12 =0,003
	2 1 / / *еи	2 e„K	5. е 11 = – 0,0041; е 12 = – 0,003
			6. возврат к п.1
			X * en 5Л \4
	25 циклов	25 циклов	25 циклов
B	Испытание с постоянным шагом	е 11=0,005 sin(ω t )
		e 12 =0,00375 sin(ω t – β)
	е 11 max=0,007; е 12 max=0,0525	β=0°	β=30°	β=60°
	L 12	C"A ---—*e	--7^ / >e
	10 циклов	15 циклов	25 циклов	25 циклов
C	1. е 11 = е 12 =0
	2. е 11 =0; е 12 =0,00425
	3. е 11 =0; е 12 = – 0,00425
	4. е 11 = – 0,0039; е 12 =0,00285
	5. е 11 =0,0039; е 12 = –0,00285
	6. е 11 = – 0,0046; е 12 =0,00195
	7. е 11 =0,0046; е 12 = – 0,00195
	8. е 11 =0,0051; е 12 =0
	9. е 11 = – 0,0051; е 12 =0
	10. е 11 =0,0046; е 12 =0,00195
	11. е 11 = – 0,0046; е 12 = – 0,00195
	12. е 11 =0,0039; е 12 =0,00285
	13. е 11 = – 0,0039; е 12 = – 0,00285
	14. возврат к п. 1
	6ц A 5, -8 JO 7A / T9 4
	50 циклов

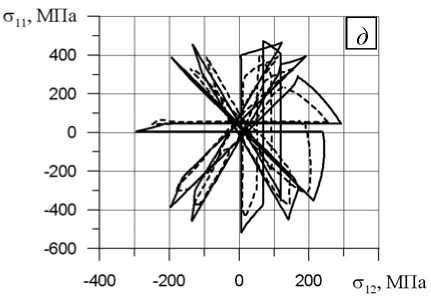
На рисунках 4, а – д показаны отклики в пространстве напряжений σ ₁₂ - σ ₁₁ на реализованные программы сложного деформирования для одного из последних циклов заданного непропорционального блока. Сплошной линией обозначены численные результаты, полученные авторами, а штриховой — опытные данные [2]. Видно их хорошее качественное и количественное совпадение.

Анализ результатов позволяет отметить существование определенных, зависимых от траектории цикла различий в степени циклического упрочнения. Так, например, блок 3 эксперимента B (Рис . 4, в ) имеет предельный уровень эквивалентного напряжения, превышающий аналогичный уровень напряжения блока 2 эксперимента B (Рис . 4, б ).

Сравнение полученных численных результатов с экспериментальными данными показывает их качественное и количественное совпадение в целом для сложного пластического деформирования конструкционных сталей при малоцикловом нагружении. Некоторые имеющееся отличия можно объяснить, например, неточностями при задании материальных параметров и тем, что при обработке экспериментальных данных принималось условие несжимаемости материала.

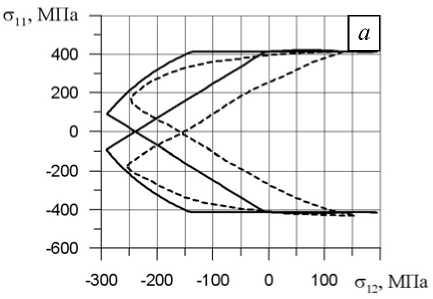
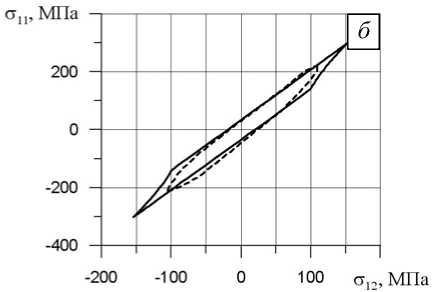
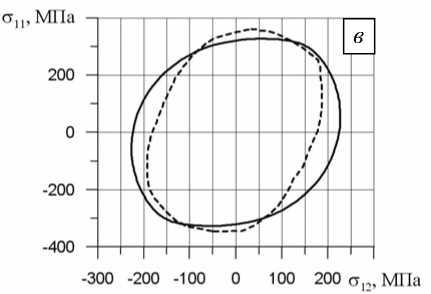
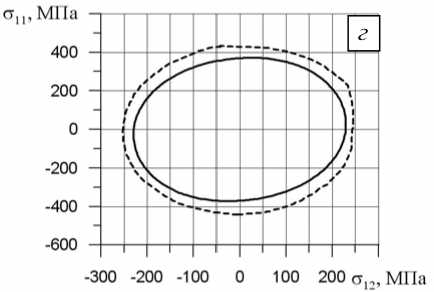
Рис. 4. Отклики в пространстве напряжений σ ₁₂ -σ ₁₁ на реализованные программы сложного деформирования на примере одного из последних циклов заданного непропорционального деформирования: эксперимент А, блок 3 ( а ); эксперимент B, блок 2 ( б ); эксперимент B, блок 3 ( в ); эксперимент B, блок 4 ( г ); эксперимент C, блок 1 ( д )

3.    Заключение

Проведена оценка адекватности определяющих соотношений модели пластичности с изотропным и кинематическим упрочнением [13, 14] путём сопоставления результатов численных экспериментов с опытными данными для сложного пластического деформирования при малоцикловом нагружении. Оценка подтвердила правильность моделирования пропорционального и непропорционального циклического пластического деформирования конструкционных материалов (металлов и их сплавов).

Отмечено, что адекватное описание сложного пластического деформирования конструкционных материалов при циклическом нагружении не возможно в рамках модельных представлений, используемых для описания монотонных процессов деформирования.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 09-08-00266-а).