Численный анализ процессов тепломассопереноса полимеров в винтовом канале экструдера с учетом теплопроводности шнека

Для многих отраслей современной промышленности большой практический интерес представляет использование полимерных композиций, обладающих уникальными эксплуатационными характеристиками. Основным способом переработки подобных нелинейно-вязких материалов на сегодняшний день остается экструзия, систематическим исследованиям проблем которой посвящено большое количество работ как отечественных, так и зарубежных авторов [1–5]. Однако следует отметить, что, несмотря на значительные успехи в развитии теоретических основ переработки полимеров, современная литература практически не содержит информации о влиянии на экструзию процессов теплопереноса в шнеке.

В математических моделях, описывающих плавление и течение полимерных материалов в винтовом канале экструдера, употребляются в основном два подхода при записи граничных условий по температуре на поверхности шнека: либо задается закон распределения температуры [6–8], либо процесс теплообмена

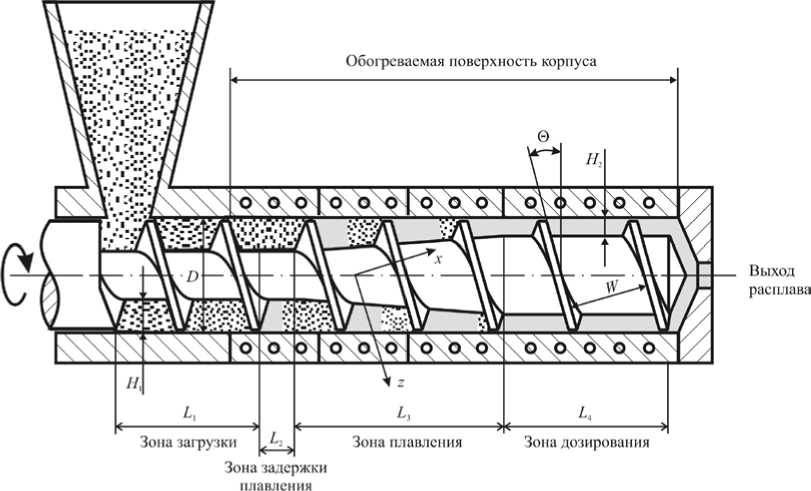
Рис. 1. Схема одношнекового пластицирующего экструдера

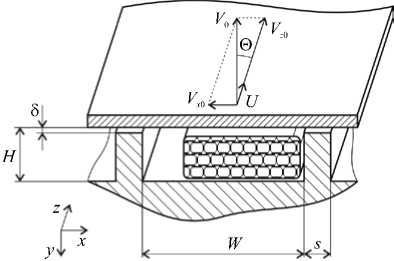
Рис. 2. Схема развернутого винтового канала

считается адиабатическим [8–11]. Численные результаты, полученные при данных условиях, имеют, как правило, существенные расхождения с результатами натурных экспериментов, что подтверждает необходимость учета процессов теплопереноса в шнеке [12, 13].

Математическое описание процессов тепломассообмена нелинейно-вязких полимерных материалов в винтовом канале пластицирующего экструдера (Рис. 1) с учетом теплопереноса в шнеке основывается на законах сохранения энергии, массы и количества движения [1, 2]. При создании модели учитываются следующие допущения: процесс стационарен при заданном массовом расходе; справедлив принцип обращенного движения, то есть рабочий канал экструдера можно развернуть в плоскость (Рис. 2); диффузионный перенос тепла вдоль канала в расплаве полимера не рассматривается; скорость и плотность твердой полимерной пробки из гранул постоянны; расплав полимера — чисто вязкая несжимаемая среда; градиенты по оси z составляющих скорости пренебрежимо малы, так как протяженность канала на два–три порядка превышает его высоту и ширину, и геометрия канала меняется по длине экструдера плавно или остается неизменной; воздействие массовых и инерционных сил мало по сравнению с влиянием сил вязкого трения.

Таким образом, процесс тепломассообмена полимера в одношнековом экструдере моделируется как течение и теплоперенос в длинном канале прямоугольного сечения (Рис. 2), верхняя стенка которого движется под углом 0 к оси канала и с неизменной скоростью V ₀ , эквивалентной окружной скорости шнека.

система дифференциальных уравнений, записанная

С учетом перечисленных допущений в динамических переменных, имеет вид:

д v    9 v

—- +—- = 0 д x    д у

д (   дvr)   д (   ( дvr   дv ]]   дP

2—I цЭ —^ I +   цЭ I —-x + —y I = —, дx (   дx )  ду I   ( ду   дx ))  дx

з д ( 2^1 Цэ дУ |

д v - )    д (   ( д v_x д v

—- I + цЭ I —- + —-ду J дx I | ду дx

д P

ду ’

д (   д v, ] д (    д v, | дP

цЭ —- I +—I цЭ —- 1 = —, дx |   дx ) ду |   ду )  дz

P m C m

д T    д T

v --+ v --+ v z дz x дx y

д T )

дУ J

дT) д Г, дT)     12

T" |+^l Xm^T I + ^V , дx J дy V дy J     2

WH

G 0 = P jj v z ( x , У ) dxdy

= const,

где x , y , z — прямоугольные координаты; v_x , v_y , v_z — составляющие вектора скорости; ц_э — эффективная вязкость; P — давление; T — температура; р m , C m , X _m — плотность, теплоемкость и коэффициент теплопроводности расплава полимера; v _z — среднеинтегральное значение скорости v_z в расплаве полимера; 1 ₂ — квадратичный инвариант тензора скоростей деформации; р — плотность полимера; W и H — ширина и высота рабочего канала экструдера; зависимость эффективной вязкости от скорости сдвига и температуры представляется реологическим уравнением вида:

Ц э =Ц о exp ( -в ( T - T o ) ) ( 1 2 /2)⁽ n " ^1У2

где ц ₀ — коэффициент консистенции расплава при температуре T ₀; в — температурный коэффициент вязкости; n — показатель аномалии вязкости; второй инвариант в уравнениях (5) и (7) определяется как

I ² = 2

Г д vx | Г д vy |

I I+1-ГI

I д х ) Voу

V v у у J

Г дvr   дv ]    ( дv, )    Г дv, |

+   / + I +1 ^z I +1^1

( ду   дx J   ( дx J   ( дy J

.

Уравнение энергии (5) для твердой пробки полимера имеет вид:

C P и — = ss дz где р$, Cs, Xs — плотность, теплоемкость и коэффициент теплопроводности твердого полимера;

U — скорость пробки, вычисляемая исходя из величины заданного расхода.

Температурное поле шнека находится из решения уравнения теплопроводности, которое для осесимметричной задачи в цилиндрических координатах выглядит так:

1 д д T -—I ^X tr— r д r V д r

= О,

где r , z — радиальная и продольная цилиндрические координаты; X _t — значение коэффициента теплопроводности или металла шнека — Х м , или полимера — Х _п.

В результате решения уравнений (1)–(3), записанных через физические переменные v_x , v_y и P , можно непосредственно получить составляющие скорости и давления в поперечном сечении канала. Но при численной реализации этих уравнений возникает ряд трудностей. Во-первых, сложно задавать и находить граничные условия для давления на тех стенках канала, на которых выполняются условия второго рода. Во-вторых, вследствие нелинейности уравнений искомое решение может быть неустойчивым. В этом случае целесообразно использовать широко известный переход к другим переменным — функции тока у и вихрю ю [14].

Уравнения, связывающие новые переменные с составляющими скоростей v_x и v_y , имеют вид:

д vx

д y

^д v y д x

ду ^vx =Т", д y

v y

ду дx

Тогда уравнения (1)–(3) перепишутся следующим образом:

. ю) + 4 ^ .^У- 2 52цЭ .5^ —2 .„ .5^ 0

d x д у д x д у     д x ²   д у ²      д у ²   д xx

д2   Л где А = —т- +--т-. Введение новых переменных позволяет избавиться от необходимости оперировать dx2 ду2

уравнением несжимаемости в явном виде, поскольку в этом случае оно выполняется автоматически. Для замыкания постановки задачи систему уравнений (4)–(14) необходимо дополнить краевыми условиями.

В представленной модели скрытая теплота фазовых переходов учитывается путем введения температурной зависимости теплоемкости. Значение коэффициента теплопроводности полимера также является непрерывной функцией температуры. Кроме того, считается, что плотности расплава и твердого полимера постоянны в пределах соответствующей фазы и в общем случае не равны друг другу.

На входе в канал экструдера известна начальная температура гранул полимера — T_{z 0} . Поле температур, полученное в конце предыдущей функциональной зоны экструдера, принимается за граничное условие в начале следующей зоны. Полагается, что температура на внутренней поверхности цилиндра экструдера есть

T = ^Т ц ( z ) ,

а на поверхности шнека

T = Tn(z), где ТЦ (z) — распределение температуры по длине цилиндра экструдера, определяемое технологическими условиями работы оборудования; ТШ (z) — температурный профиль шнека, рассчитываемый итерационно путем совместного решения уравнений (4)–(9), (11)–(14) и уравнения теплопроводности (10).

Граничные значения функции тока и вихря, компоненты скорости v_z удовлетворяют условию прилипания жидкости к твердым непроницаемым поверхностям. При этом значение ю вычисляется по формуле Вудса второго порядка точности:

V| в = ⁰ ,

52V ю| B = дг 2 ,

dZ v          = V,,, = V, cos 0, v = U , v          = 0, z|x=[0+W], у=0 z0 0         ,        zx=xГ, у=уГ        ,         zx=xШ, у=ущ       ,

где индекс B соответствует твердой непроницаемой границе; Z — нормаль к поверхности границы B ; x _Г, y _Г — координаты границы между твердой и жидкой фазами, изменяющиеся при продвижении пробки по каналу и требующие переопределения на каждом шаге по длине канала; x _Ш, y _Ш — координаты поверхности шнека.

При решении задачи теплопроводности (10) левая ( z = 0 ) и правая ( z = L ₀) границы шнека и полимерного слоя (Рис. 3) считаются адиабатическими:

^{d zz} r = ( R 3 ^ R 5 )

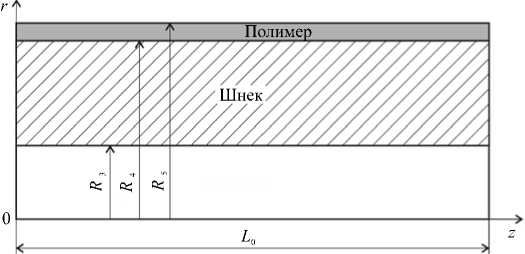
Рис. 3. Схема для расчета теплообмена в шнеке

где R ₃ — радиус внутреннего отверстия шнека; R ₅ — радиус, измеряемый по поверхности полимерного слоя; L ₀ — длина шнека.

На внутренней поверхности шнека ( r = R ₃) тепловой поток отсутствует:

^U r z = (0 ^ L 0 )

На поверхности тонкого полимерного слоя ( r = R 5 ), прилегающего к шнеку, выполняется условие первого рода:

Tz=(0+L0)   Tn (z), где ТП (z) — температурная зависимость, устанавливаемая в ходе решения задачи пластицирующей экструзии, описываемой уравнениями (4)–(9), (11)–(14).

На границе контакта материалов с разными теплофизическими характеристиками ( r = R 4 ) соблюдаются равенства как температур, так и тепловых потоков:

. d t

Л , о r

z = (0 + L o )

1 8 T

-Лм^ dr

, z=(0+Lo)

Т + .    = Т^-,  .

Iz = (0 + L o )     ¹ |z = (0 + L o ) .

Таким образом, система уравнений (4)–(14), замкнутая граничными условиями (15)–(23), является математической моделью процесса движения, плавления и течения полимера в винтовом канале одношнекового экструдера с учетом теплопроводности шнека.

На сегодняшний день при моделировании тепломассообмена широко применяется метод конечных разностей (МКР) и метод конечных элементов (МКЭ). Основным преимуществом МКЭ является возможность получать высокоточное решение задач со сложной геометрией исследуемой области. МКР эффективен в случаях, когда границы расчетной области совпадают с координатными плоскостями или параллельны им. Поскольку в настоящей работе исследуемая область имеет достаточно простую геометрию, целесообразно прибегнуть к МКР [14–19].

Для численного решения задачи на основе представленной математической модели авторами разработан программный комплекс по расчету процессов тепломассопереноса полимерных материалов в каналах одношнековых экструдеров (Universal Screw 12) [20], который позволяет не только находить количественные параметры течения и плавления полимера в каналах экструзионного оборудования, но и визуализировать их. Расчет процессов тепломассообмена нелинейно-вязких полимерных сред в рабочем канале пластицирующего экструдера с учетом теплопроводности шнека осуществляется поэтапно.

На первом этапе с помощью итерационной процедуры решается пространственная задача тепломассопереноса полимера в винтовом канале одношнекового экструдера, описываемая выражениями (4)–(9), (11)–(19), причем на первой итерации температурный профиль шнека вычисляется по эмпирическому уравнению, предложенному Элбирли и Линдтом в работе [21]. Результатом итерационного расчета являются поля температур, скоростей, изменение давления и градиента давления по длине рабочего канала экструдера. Кроме того, формируется граничное условие первого рода для задачи определения температурного поля шнека, которая реализуется на втором этапе (ей отвечают уравнения (10), (20)–(23)). Шнек, обладающий высоким значением коэффициента теплопроводности, заменяется толстостенным полым стальным цилиндром с постоянными по длине внутренним ( R ₃ )

и внешним ( R4 ) радиусами (Рис. 3). Вследствие переменной глубины нарезки канала внешний радиус берется усредненный.

Полученные в поперечных сечениях канала температурные поля полимера используются в расчете распределения температуры на поверхности тонкого слоя пластиката, прилегающего к шнеку (Рис. 4). При решении уравнения теплопроводности (10) данный слой считается неподвижным, а его толщина равняется шагу расчетной сетки по высоте рабочего канала экструдера.

Далее, для каждого поперечного сечения винтового канала экструдера находится средневзвешенная

Рис. 4. Схема для расчета средневзвешенной температуры

температура в слое, прилегающем к шнеку. Формула для расчета средневзвешенной температуры в слое N y - 2 с учетом влияния теплоты, подводимой от корпуса экструдера через гребни шнека, записывается следующим образом:

T = Тк W^ + Тр^ж + TnWT          ( ср     W^ + WK + WT   ,         ( } где Wж , Wт , WГр — ширина области, занимаемой расплавом, твердой пробкой и гребнем шнека; Tк — температура корпуса на соответствующей длине

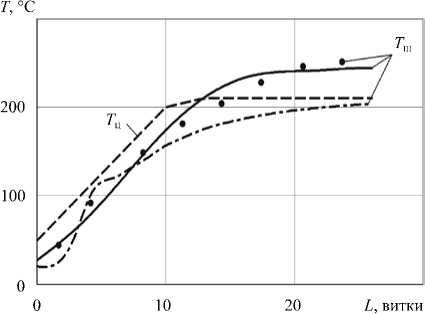
Рис. 5. Изменение температур корпуса ( T _Ц ) и шнека ( T _Ш ) экструдера по длине; точки – данные эксперимента из работы [23]; сплошная линия – численный расчет по предложенной математической модели; штрихпунктирная линия – расчет по эмпирическому уравнению [21]; штриховая линия – температурный профиль цилиндра экструдера

канала; T _р , T _п — средняя температура расплава и твердого полимера в слое N y - 2, соответственно, на ширине W _ж и W _т . Совокупность значений T _ср вдоль канала согласуется с граничным условием (22), которое является связующим итерационной процедуре расчета температурного поля шнека.

При решении стационарной задачи теплопроводности, описываемой уравнением (10) с граничными условиями (20), (21), (23) и переопределяемым граничным условием (22), рассчитываются поля температур в тонком слое пластиката и теле шнека. Они позволяют отслеживать изменение температуры по длине границы «полимер–металл (шнек)» и уточнять граничное условие (16) для решения задачи тепломассопереноса полимера в винтовом канале пластицирующего экструдера на второй итерации расчета общей задачи.

Последовательное решение двух задач с уточнением граничных условий (22) и (16) представляет собой итерационный процесс, который продолжается до выхода температурного профиля шнека на установившийся режим. В результате получается набор характеристик процесса переработки полимерного материала в одновинтовом пластицирующем экструдере с учетом геометрических и технологических параметров, а также свойств перерабатываемого материала и теплопроводности шнека.

Для верификации предложенной математической модели проведено сравнение найденной по ней численно температуры шнека с экспериментально замеренной [22, 23]. Из рисунка 5 видно, что максимальное различие между численными и экспериментальными данными не превышает 7%.

Таким образом, предложенная пространственная математическая модель процессов тепломассопереноса нелинейно-вязких полимеров в рабочих каналах пластицирующих экструдеров, учитывающая фазовые переходы материалов и теплопроводность шнека, позволяет достаточно точно описывать температурный профиль шнека и, следовательно, создавать более полную картину течения и плавления полимеров при экструзии.

Далее на конкретном примере демонстрируются возможности разработанного авторами программного комплекса «Universal Screw 12» [20].

Численное исследование процессов тепломассопереноса полимеров в винтовом канале экструдера с учетом теплопроводности шнека проведено для промышленного экструдера с геометрическими размерами, представленными в таблице 1, при следующих исходных данных: массовая производительность экструдера G0 = 0,06 кг/с; число оборотов шнека NШ = 60 об/мин; начальная температура гранулята Tz0 = 20°С; температура цилиндра экструдера ТЦ на первых семи витках линейно растет с 92°С до 200°С, далее остается неизменной; плотность металла шнека рш = 7600 кг/м3; удельная теплоемкость Cш = 490 Дж/(кг°С), коэффициент теплопроводности Хш = 40 Вт/(м^°С). Теплофизические и реологические свойства перерабатываемого полимера приведены в таблице 2 и на рисунке 6.

Таблица 1. Геометрические характеристики экструдера

Внутренний диаметр цилиндра (корпуса), мм	160,0
Наружный диаметр шнека, мм	159,4
Шаг винтовой нарезки, мм	160,0
Ширина канала W , мм	137,3
Ширина гребня винтовой нарезки s , мм	15,3
Длины геометрических зон загрузки, сжатия и дозирования, витки	10/10/7
Суммарная длина шнека, витки	27
Глубина канала в зоне загрузки, H 1 , мм	16
Глубина канала в зоне дозирования H 2 , мм	4
Угол подъема винтовой линии © , град	17 ° 39 '
Диаметр отверстия в шнеке, мм	48

Таблица 2. Реологические и теплофизические свойства перерабатываемого полимера

Материал	n	Ц о , Па - с n	Т о , ° С	в , 1/ ° С	T n , ° С	р s , кг/м3	р m , кг/м 3	X s , Вт/(м- ° С)	X m , Вт/(м- ° С)
ПЭНП	0,44	10825	160	0,018	110	919,0	779,0	0,335	0,182

Поскольку на процессы течения и теплопереноса в винтовом канале экструдера существенное влияние оказывает распределение температуры по длине шнека, важной является оценка подходов к его определению. На рисунке 7 (кривая 1 ) приведено это распределение с учетом процесса теплопроводности, вычисленное согласно представленной математической модели в программном комплексе «Universal Screw 12»; кривая 2 получена исходя из эмпирического уравнения [21]; кривая 3 отвечает случаю отсутствия теплообмена между перерабатываемым полимером и шнеком (адиабатические условия на поверхности шнека); кривая 4 — результаты из статьи [24].

СЮ’3,

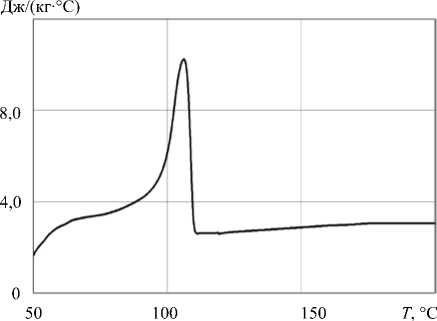
Рис. 6. Температурная зависимость удельной теплоемкости перерабатываемого полимера

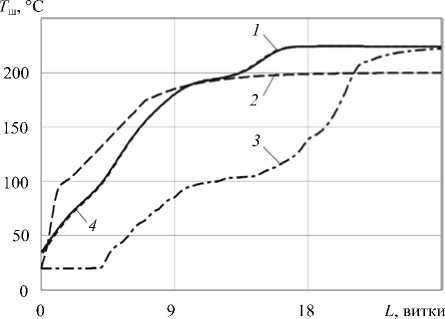
Рис. 7. Изменение температуры по длине шнека

В работе [24], в отличие от предложенного в данной работе метода расчета температурного поля шнека, задача теплопроводности шнека тоже решалась численно, но с использованием программного комплекса ANSYS (кривая 4 , Рис. 7). Из рисунка видно, что расхождение между кривыми 1 и 4 незначительное, не превышает 1%. Однако существенным недостатком расчета температурного профиля шнека в пакете ANSYS является невозможность организовать автоматическую итерационную процедуру совместного решения задач тепломассопереноса полимера в винтовом канале экструдера и определения температуры шнека. В то же время объединение всех вычислений в рамках программного комплекса «Universal Screw 12» позволяет значительно снизить трудоемкость вычислительных экспериментов.

Решение задачи тепломассопереноса полимера в винтовом канале экструдера осуществляется по маршевой схеме, в соответствии с которой на каждом шаге сетки по длине канала в узлах дискретизированных поперечных сечений канала находятся температуры, значения компонент вектора скорости, температуры материала (средняя, минимальная и максимальная), градиент давления и давление. Пакет «Universal Screw 12» обладает возможностью представлять результаты вычислений в виде картин, удобных для зрительного восприятия. На рисунке 8 приводятся характерные температурные поля и поля составляющих скорости в поперечном сечении канала экструдера на длине 12,5 витков, которые отображаются в виде трехмерных поверхностей, позволяющих визуально наблюдать наиболее нагретые области расплава и контур твердой фазы. По полям скоростей можно оценить характер течения расплава полимера в экструдере. На рисунке 8 хорошо видна интенсивная поперечная циркуляция перерабатываемого материала. На рисунке 9 показаны графики изменения минимальной, средней, максимальной температур полимера по длине канала экструдера, температурные профили корпуса и шнека.

По кривым видно, что максимальная температура полимера в зоне задержки плавления резко возрастает. Это обусловлено появлением диссипации тепла в тонком слое расплава у внутренней поверхности цилиндра экструдера, вследствие чего существенно ускоряется плавление твердой фазы со стороны корпуса. Разница между максимальной температурой расплава полимера и температурой корпуса в конце зоны задержки плавления составляет 35 ° С.

Внутренняя область пробки полимера прогревается достаточно медленно, поскольку в твердой фазе рост температуры обусловлен только процессами теплопроводности при низком значении коэффициента теплопроводности, что видно по изменению минимальной температуры материала (Рис. 9). К концу зоны плавления размеры пробки уменьшаются, скорость ее прогрева значительно увеличивается,

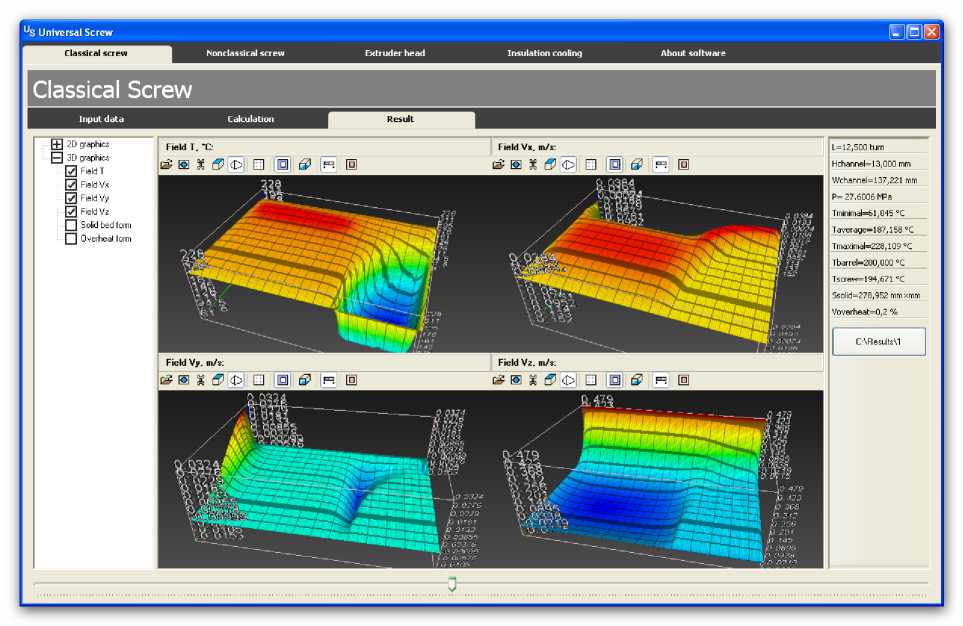
Рис. 8 . Поля температуры и скоростей в канале экструдера на длине 12,5 витков

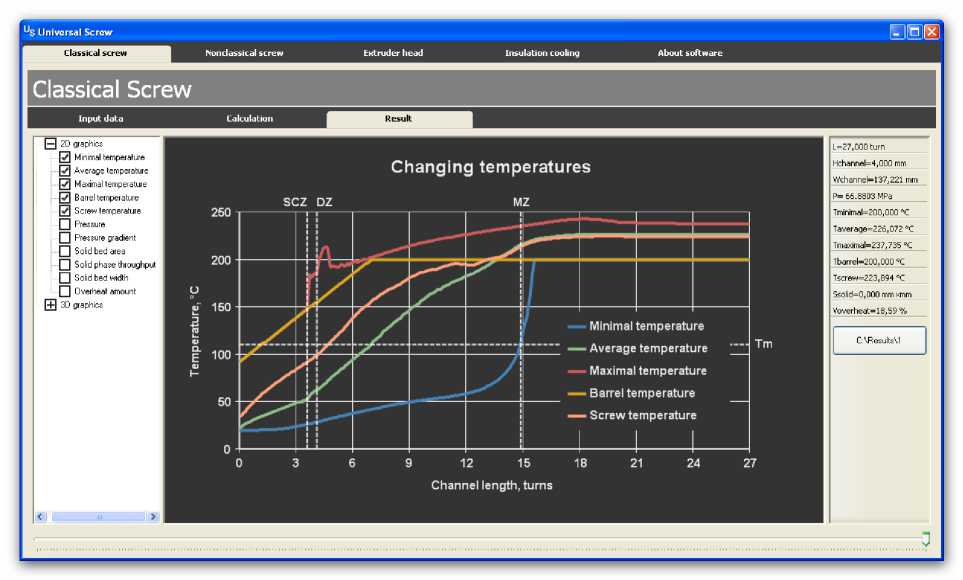
Рис. 9. Распределение температур по длине канала экструдера а при переходе к зоне дозирования на длине примерно одного витка в поперечном сечении канала происходит выравнивание температурного поля за счет интенсивной конвекции расплава полимера. При этом минимальная температура увеличивается с 110°С до 200°С. На выходе из канала экструдера максимальная температура расплава полимера составляет около 238°С, а средняя — 226°С. Это указывает на значительный вклад диссипативного источника в общий тепловой баланс при переработке пластиката с заданными свойствами.

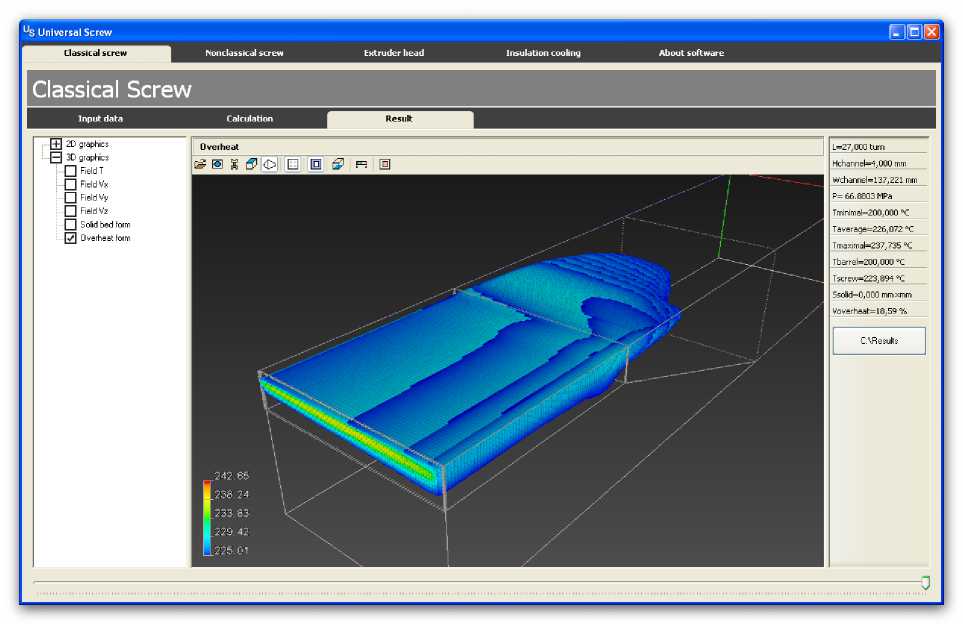
Рис. 10. Распределение областей локальных перегревов в канале экструдера

На рисунке 10 представлена область канала экструдера, в которой температура расплава полимера превышает 225 ° С. Локальный перегрев возникает на двенадцатом витке канала экструдера в геометрической зоне сжатия. Перегретый материал занимает практически всю ширину канала и располагается около внутренней поверхности цилиндра экструдера. Его объем достигает 18,59% от общего объема расплава полимера в рабочем канале экструдера. Следовательно, если принимать в расчет теплоперенос в шнеке, то можно точнее подбирать температурные режимы работы оборудования, что является исключительно важным при переработке большинства современных полимерных композиций [25].

Выводы

На основе предложенной математической модели и алгоритма ее реализации разработан пакет «Программный комплекс по расчету процессов тепломассопереноса полимерных материалов в каналах одношнековых экструдеров» («Universal Screw 12»). Для демонстрации его возможностей проведено численное исследование процесса переработки полимера на промышленном экструдере. Показано, что комплекс позволяет:

– учитывать теплоперенос в шнеке при моделировании процесса экструзии;

– численно получать картины течения и плавления полимера в каналах экструзионного оборудования;

– представлять результаты в удобном для анализа виде;

– снижать уровень локальных перегревов перерабатываемого полимера путем изменения параметров технологического режима;

• –    подбирать рациональные технологические режимы переработки при переходе на новые полимерные материалы;

• –    облегчать поиск технических решений при разработке новых конструкций шнеков экструдеров за счет существенного снижения затрат на натурные эксперименты.

Работа выполнена при финансовой поддержке РФФИ (проект №13-08-96034p-Урал_а).