Численный анализ режимов работы газокапельного химического реактора идеального вытеснения

Введение. Протекание экзотермических реакций в двухфазных средах характерно для широкого круга процессов, которые связаны с химическим взаимодействием горючих компонентов, находящихся в различных агрегатных состояниях. Эти процессы лежат в основе современных способов сжигания жидкого и твердого топлива, используются в энергетике, авиационной и ракетной технике, химической технологии и т. д.

В последние годы получили дальнейшее развитие представления о процессах горения в гетерогенных средах, в том числе на основе построения корректных математических моделей и разработки новых подходов и приемов их численного решения.

В данной работе рассматривается модель двухфазного адиабатического газокапельного химического реактора идеального вытеснения и ее численное решение, основанное на применении неявных схем с разностями против потока.

Математическая модель. Модель такого реактора, записанная в соответствии с принципом взаимно проникающих континуумов, представляет собой в безразмерных переменных следующую систему дифференциальных и алгебраических уравнений:

dp dp V d t    dx0

dc2P dc2p VA

81      dxDe ;

Sp c i Y b dp cVY b^ A m        ₍₍. L ^e SY.

at       ax     De a W Pe dx2 ’ dpciYa 8pc1VYa       ^^ Le 8 Ya .

at ⁺ ax         “ W ⁺ Pe ax 2 ;

(p q9 1 ) + ^ (p c A V ) =- A ^ Q + Da W + A m M 9 w + -D DA⁹¹; d t      'dx            Pe y Pe Pe d _x ²

c 21 -D (pc292) + c 21   (pc 262V) = Am (Q - Me / у-c 21M 9 w);

о t             оx

Yb + Ya + Y = 1;

ту _ уnb vna _e( ^{9 1 + (} ^^{0 - 1)/ в} )■

W - Yb Ya exp^ p91 +$o J;

Q - nrq;

M — nr ф;

Ф = 1

lnl 1 +

lnl 1 +

q =1

где 0 1 =

E ( T — T o ).

RT _* ²

c_{p 2}

^c 21 =     ;

c p 1

—P

^P1 1 + 30 1 / V

^P    « 1 / p 1 + « 2 / ^p 2 ;

0 1 — 0 w

£ / Y + C 21 (0 1

—-- I , апёе { 0 1 <0 d } U { Y a <  Y d } , ⁰ w ) у

0 1 — 0 w + Y a /( Qy )

£/ _Y + C 21 (0 1 —0 _w ) J’

апёе { 0 1 >0 d } П { Y a > Y d } ;

'0 1

>1

—

—

0 w = min 0_g61,

0 w , апёе { 0 1 <0 _d } U { Y a <  Y d } ,

0 w + Y a /(Оу), апёе { 0 1 >0 d } П { Y a >  Y d } ;

⁰ 1 + 9 o / P + ^{( 0} + 3 o / 3) V П 21 Х 21 ^p 2 / ^p 1    3₀

V

= E(T 2 — T 1o ) .

^{1 +} V « 21 ^X 21 ^p 2 / ^p 1

—

2 =

RT _* ²

;

-*-• c1            ;

P 10

c = -P^

^c 2           ;

P 10

p=

;

Y =

в ’ У

RT * ² C p 1 . .= T o ;

Eq_T        T _*

q U

^{£         ;}

qT

.  _ X 2 .    n _a _ WL .

^X 21 =   ;   ^Da = -    ;

^X 1            ^p o V o

Pe = VL ;

a

ML ² m           ;

a P o

a =

xl

C p 1 P o

;

Le = D ; M = a

k 0 s 0 n 0 ; c p 1

W = k • exp l —

-E - b V Vb. x^-RT* J; V V o ; L

V 0 t t L "

Здесь, по аналогии с работой [1], приняты следующие обозначения: T1, T2 — температура несущей (газовой) и дисперсной (жидкой) фаз соответственно; Ya , Yb , Yï — концентрация компонентов газовой фазы окислителя, газообразного горючего и продукта реакции соответственно; c1, c2 — массовая доля газовой и жидкой фаз соответственно; p — эффективная плотность; М — скорость парообразования; W — скорость химической реакции; Q — член, описывающий межфазный теплообмен; k0 — коэффициент теплоотдачи от газа к каплям; s0 — площадь поверхности капель в монодисперсной, подающейся в реактор смеси; n0 — числовая концентрация капель во втекающей смеси; V — скорость потока смеси; Y — время; x — координата; Q — стехиометрический коэффициент; k, E, R, na , nb — соответственно предэкспоненциальный множитель, энергия активации, универсальная газовая постоянная, показатели порядка химической реакции по каждому из реагентов в законе Аррениуса; cp1,cp2 — изобарная удельная теплоемкость несущей и дисперсной фаз соответственно; Х1, X2  — коэффициенты теплопроводности фаз; qT, qU — удельная теплота реакции и теплота парообразования соответственно; T* — масштабная температура; Pe, Da, Le — критерии Пекле, Дамкёлера и Льюиса соответственно. Индекс «ноль» соответствует параметрам смеси на входе в реактор.

Граничные условия задаются следующим образом:

• —    на входе в реактор, при x = o, t > o:

d01-p_e   d Y L-Zefy- Z Y l -Pe/y-yy

⁰ 2 = ⁰ 2o , V = 1, ^C 2 = ^C 2o ,   ^C 1 = ^{1   C} 2o ,       = ^Pe ^⁰ 1 ,       =_T   ⁽ Y b    Y b o ),   -. = _T⁽ Y a    Y a o ) ;

d x          d x Le           d x Le

• —    на выходе из реактора, при x = 1, t > o:

d01 =aY, =57^ = o dx    dx    dx    .

В качестве начальных условий принимаются следующие: при t = 0,0 <  x < 1: 0 1 = 0_u,

6 2 = 6 2, , Y b = Y b _f, Y a = 1 - Y b _f, c 2 = c 2^ , c = 1 - c 2^ , V = 1.

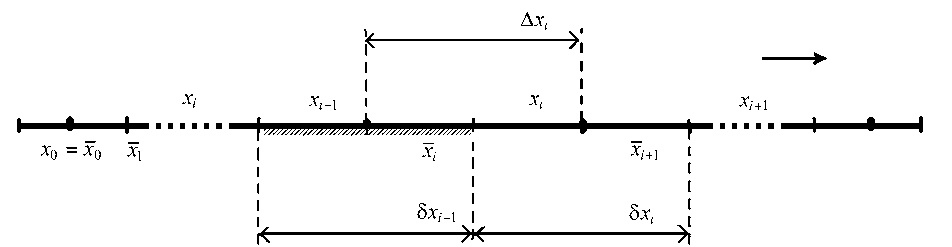
Численная аппроксимация модели. Дискретный аналог системы (1)—(15) строится на основе метода донорных ячеек [2]. При этом физическое пространство [0, 1] покрывается сеткой с узлами xt (i = 0, 1, ..., n + 1), xi — грани контрольных объемов (i = 0, 1, ..., n), xi = ih, x0 = 0, x = h2 + (i -1)h, xi = 1. Это схематично показано на рис. 1. Контрольные объемы не имеют общих внутренних точек и покрывают все пространство.

^xn   ^xn +1

Рис. 1. Иллюстрация принципа построения дискретного аналога математической модели реактора

Для получения дискретного аналога присутствующие в модели дифференциальные уравнения интегрируются по каждому контрольному объему [ x i - 1 , x i ] . Производные первого порядка, появляющиеся в результате интегрирования вторых производных, заменяются отношениями конечных разностей. Значения источниковых членов вычисляются в узловых точках и для текущего значения переменной времени. В результате такой процедуры получаем систему сеточных уравнений, представляющую собой неявную, консервативную, конечно-разностную аппроксимацию системы уравнений (1)—(6). Вместе с уравнениями (7)—(15), записанными в узловых точках, она является замкнутой. Расчет значений переменных в узлах сетки на каждом шаге осложняется тем, что полученная система — нелинейная. Поиск ее решения на каждом шаге по переменной времени проводится методом простых итераций. Сам шаг по времени подбирается автоматически в зависимости от количества выполняемых на нем итераций.

При проведении численных экспериментов в качестве базовых были приняты значения параметров, типичные для смесей углеводородов с воздухом и приблизительно соответствующие системе « н -декан — воздух» [3].

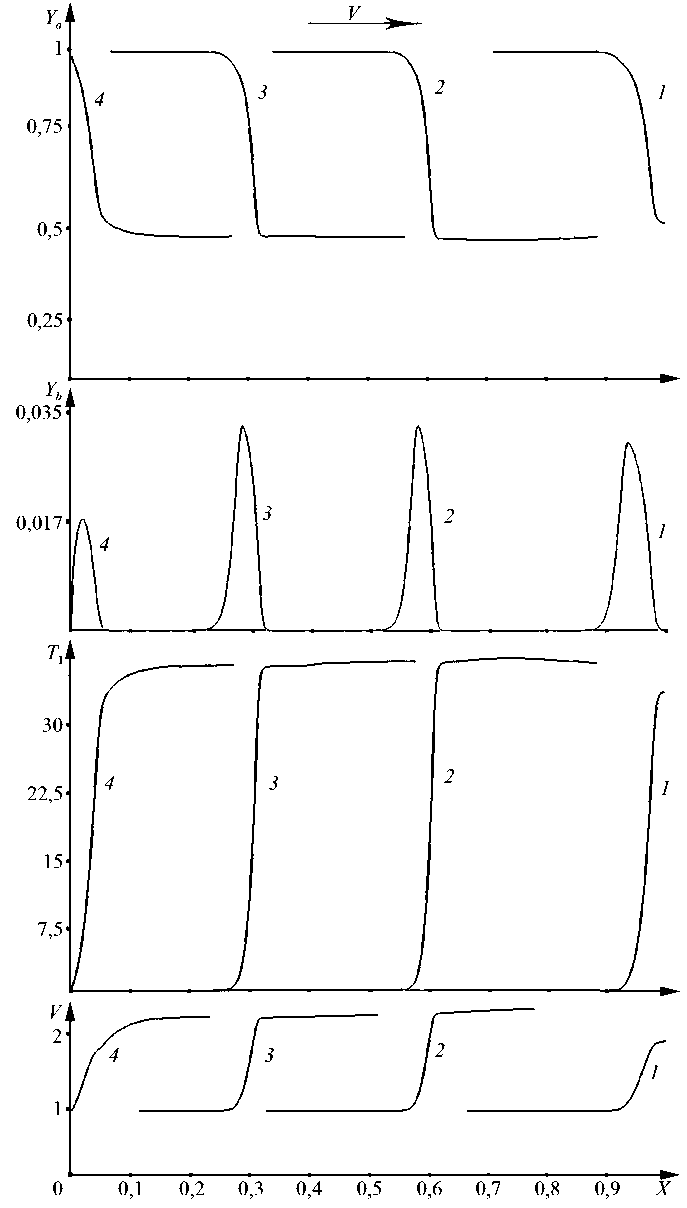
Главное внимание уделялось вариациям критериев Pe, Da, A m , которые непосредственно связаны с определяющими процесс параметрами, такими, как скорость подачи смеси, длина реактора, скорость химической реакции, размеры частиц. В зависимости от значений чисел Pe, Da, A m и начальных условий могут наблюдаться как устойчивые высокотемпературные режимы горения смеси в реакторе, так и режимы с незначительной степенью химического превращения компонентов и невысокой температурой смеси на выходе из реактора. Для некоторой области значений параметров наблюдаются неустойчивые режимы работы реактора. На рис. 2 приведены распределения температуры и компонентов газовой фазы, а также скорости смеси в различные моменты времени, полученные при следующих значениях критериев Da = 0,29, Pe = 20, A m = 15000. Как видно из рисунка, направление течения смеси — слева направо, значение пространственной координаты x = 0 соответствует входу в реактор, а значение x = 1 — выходу из него. Газокапельная смесь поджигается на выходе из реактора, что выражается в поддержании в течение начального незначительного промежутка времени высокотемпературного (порядка адиабатической температуры горения соответствующей газовой смеси) теплового импульса.

а )

Рис. 2. Пульсирующий режим работы реактора.

Распределение концентраций компонентов газовой фазы, температуры газа, скорости смеси в реакторе в различные моменты времени (см. также с. 645): а — зона химической реакции распространяется влево; б — зона химической реакции потоком сносится вправо; цифры на графиках соответствуют моментам времени:

1 — t = 0,01; 2 — t = 0,08; 3 — t = 0,16; 4 — t = 0,21; 5 — t = 0,22; 6 — t = 0,33; 7 — t = 0,45; 8 — t = 0,59

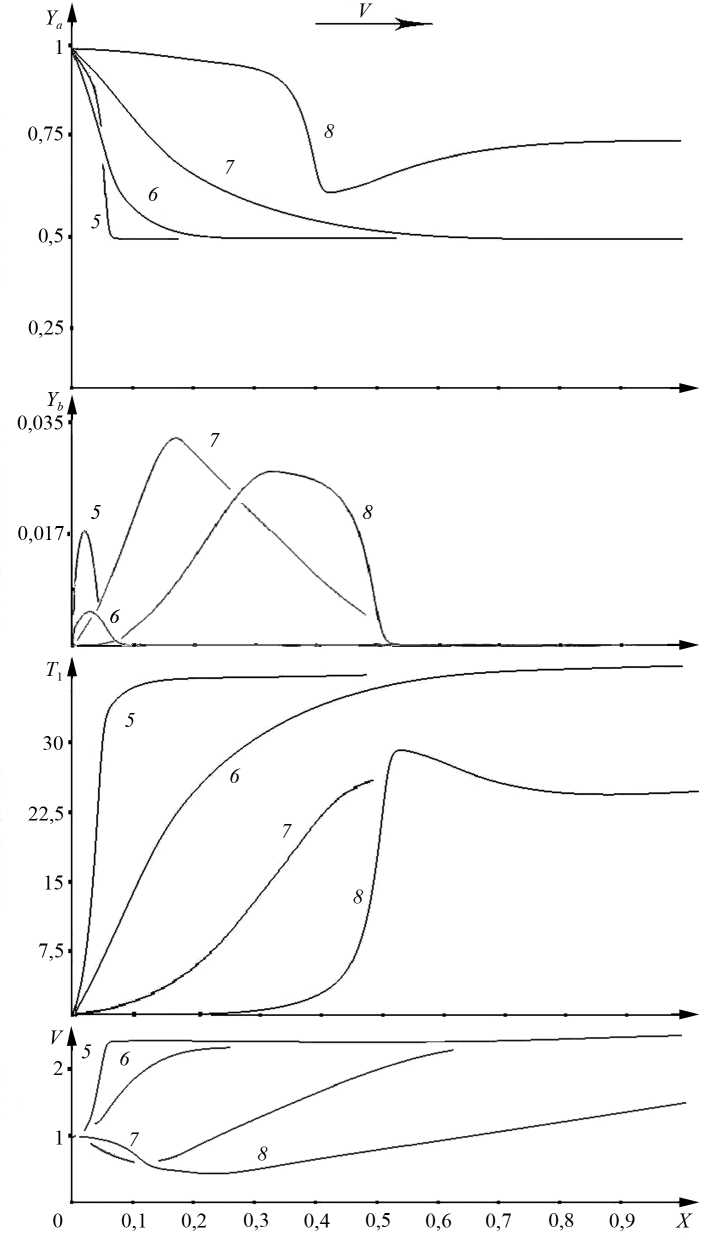
б )

Рис. 2. Окончание (начало см. на с. 644)

Образовавшаяся после этого зона горения распространяется в сторону входного отверстия (кривые 1—4 на рис. 2, а). Достигнув ближайшую окрестность сечения x = 0, зона пламени распадается в связи с нехваткой газообразного топливного реагента, производимого в процессе испарения капель. В дальнейшем в газокапельной смеси, втекающей в реактор и сносимой вниз по течению, вследствие испарения происходит накопление пара жидкости (кривые 5—8 на рис. 2, б) и, соответственно, увеличение скорости химической реакции.

На некотором удалении от входного сечения происходит самовозгорание смеси (кривые 8 ), а вновь сформировавшаяся зона пламени движется навстречу набегающему потоку. Тем самым реализуется пульсирующий режим работы реактора.

Заключение. Разработана методика численного решения одномерной задачи о развитии процессов тепло- и массопереноса в газокапельном химическом реакторе идеального вытеснения. Для значений управляющих параметров, соответствующих высокотемпературным режимам работы реактора, развитый подход позволяет отслеживать формирование и распространение волны горения в потоке газа с каплями.