Численный анализ собственных частот колебаний и статических напряжений радиальных рабочих колес энергетических турбомашин для АПК
Автор: Репецкий Олег Владимирович, Хоанг Динь Кыонг
Журнал: Агротехника и энергообеспечение @agrotech-orel
Рубрика: Технологии и средства технического обслуживания в сельском хозяйстве
Статья в выпуске: 4 (33), 2021 года.
Бесплатный доступ
Радиальные рабочие колеса турбомашин - это сложные вращающиеся детали машин, являющиеся критическими важными деталями для определения долговечности и безопасности компонента. Структурные повреждения оказываются конструкцию вибрацией, отрывания одной или нескольких лопастей. Требование структурной целостности часто противоречит облегчению конструкции и высокой аэродинамической эффективности. Так, что в процессе проектирования задача исследования прочности и надежности радиальных рабочих лопаток от напряжений и собственных частот колебаний радиальных рабочих лопаток энергетических турбомашин очень важна. Также при проектировании радиальных лопаточных дисков, применяемых в АПК, проводится множество численных и экспериментальных испытаний. Испытания требуются большие усилия на испытательных стендах и образцах. Таким образом, расчеты на прочность и компьютерное моделирование технических процессов радиальных рабочих колесах, применяемых в АПК, являются актуальными на стадиях проектирования, доводки и практической эксплуатации. Эти расчеты позволяются существенно сократить объем дорогостоящих экспериментальных исследований и уменьшить сроки конструирования новых машин.
Радиальная лопатка, метод конечных элементов, рабочее колесо, собственная частота, статическое напряжение, турбомашина, форма колебаний
Короткий адрес: https://sciup.org/147235494
IDR: 147235494 | УДК: 519.6:62-135
Текст научной статьи Численный анализ собственных частот колебаний и статических напряжений радиальных рабочих колес энергетических турбомашин для АПК
Введение. Для тестового измерения собственных частот колебаний радиального рабочего колеса, применяемого для вентиляционных процессов в АПК, с учетом вращения был разработан экспериментальный стенд [1] где возбудитель - магнит был установлен в непосредственной близости от опорной плиты. Вибрационный отклик регистрировался тензодатчиком, который был приклеен к опорной пластине в местах сильных радиальных деформаций собственных форм и подавался на быстрый преобразователь Фурье (БПФ) через передаточные контактные кольца. Вся установка для измерения собственных частот радиального рабочего колеса при вращении показана на Рис. 1.
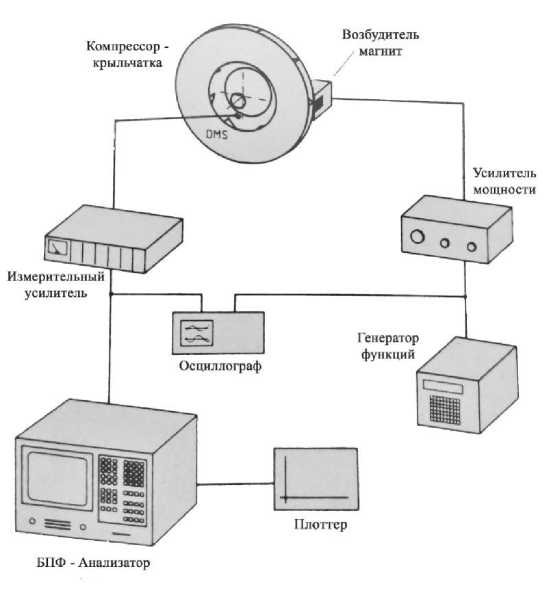
Рисунок 1 – Экспериментальная установка для анализа собственных частот колебаний радиальных рабочих колес энергетических турбомашин с учетом вращении
В спектре отклика может видеть четкие пики, которые можно четко отнести к ранее определенным собственным частотам. Частоты немного сдвинуты по сравнению с частотами при измерении с электродинамическим возбудителем. Так, что можно проследить до его массового влияния, а также многократных реконструкций за это время и связанных с этим незначительных системных изменений. Все результаты эксперимента для измерения собственных частот радиального рабочего колеса c 10-ю лопатками представлены в таблицах [1].
Материалы и методы исследования

а
б
Рисунок 2 — Радиальное рабочее колесо c 10-ю лопатками (а - общий вид, б - конечноэлементная модель)
Основные механические характеристики имеют вид: материал рабочего колеса -сталь, модуль Юнга - 2,1.10 5 Мпа, плотность - 7850 кг/м 3 , коэффициент Пуассона - 0.3. Общий вид рабочего колеса представлен на Риc. 2а, где конструкция объекта была жестко закреплена по ободу диска. В качестве конечноэлементной модели применяется конечный элемент ТЕТ10 программы ANSYS WORKBENCH с общим количеством конечных элементов - 58382 и 115590 узловыми точками. Количество степеней свободы составляет -346770 (Рис. 2б).
Уравнения движения с использованием МКЭ для статики и свободных колебаний могут быть описаны в виде [7,8,9]:
( [ K e ] + [ K g ] + [ K r ] ) ' 5 } = { F n} + { F t } + { F G } , (1)
а для свободной вибрации:
[ M ] { » } + [ C ] { 5 } + ( [ K E H K G ] + [ K R ] ) 5 } = 0 - (2)
где { 5 } - вектор смещения, [ KE ] и [ M ] - матрицы упругой жесткости и массы, соответственно, [ KG ] - матрица геометрической жесткости, зависящая от скорости и температуры, [ K R ] - дополнительная матрица жесткости, возникающая в результате вращения, { F } , { F T } , { F G } - векторы, соответствующие силам я вращения, температурой и давлением газа соответственно, [ C ] - матрица Кориолиса.
Результаты и обсуждение
На Рис.3 представлены 6-ть основных форм колебаний для радиального рабочего колеса с 10-ю лопатками. Каждая форма обладает разнообразной характерной деформацией, по критерию количества узловых диаметров и на числа узловых окружностей (n / m), определяющийся форму 3 - 0/0, форму 1 - 1/0, форму 14 - 0/1, форму 7 - 1/1, форму 5 - 2/0, форму 10 - 5/0.
Таблица 1. Значения собственных частот для радиального рабочего колеса в эксперименте и программах ANSYS WORKBENCH и BLADIS + [1].
|
Форма n / m |
Эксперимент, Гц |
Собственные частоты без учета вала, Гц (ANSYS- слева и BLADIS + справа). |
Отклонение Δf, % |
|
|
0/0 |
- |
81,075 |
- |
- |
|
1/0 |
44 |
43,675 |
- |
0,74 |
|
0/1 |
- |
443,61 |
- |
- |
|
1/1 |
- |
395,45 |
- |
- |
|
2/0 |
341 |
342,91 |
349,0 |
0,56 |
|
5/0 |
- |
413,04 |
402,1 |
- |
Анализ таблицы 1 показал что, значения собственных частот колебаний от эксперимента для формы 1 отклоняется на 0,74%, а для формы 5 на 0,56%.
На следующем этапе анализа рассмотрены расчеты статических напряжений с учетом вращения радиального рабочего колеса.
Для анализа прочности и надежности радиального рабочего колеса при проектировании компрессорного колеса, выполнены численные исследования статического напряженно-деформированного состояния (НДС) и собственных частот колебаний при оборотах вращения: 5 (1/s), 10 (1/s), 15 (1/s), 20 (1/s), 30 (1/s), 40 (1/s), 50 (1/s), 60 (1/s).
Рисунок 4 и таблица 2 показываны расчеты статического напряжения σ э в колесе с учетом вращения.
Таблица 2 - Значение статического напряжения σ э для радиального рабочего колеса с 10-ю лопатками с учетом вращения, МПа
|
Скорость вращения колеса, 1/s |
Experiment, MPa |
Максимальные статические напряжения, Мпа |
Отклонение Δf, % |
|
5 |
- |
2,0511 |
- |
|
10 |
- |
8,2046 |
- |
|
15 |
- |
18,460 |
- |
|
20 |
32 |
32,818 |
2,56 |
|
30 |
- |
74,841 |
- |
|
40 |
- |
131,270 |
- |
|
50 |
- |
205,11 |
- |
|
60 |
- |
295,36 |
- |
Таблица 3 - Расчеты значения собственных частот колебаний для радиального рабочего колеса 10-и лопаток с учетом вращения, Гц
|
Форма |
Собственные частоты колебаний, Гц |
||||||||
|
0 (1/s) |
5 (1/s) |
10 (1/s) |
15 (1/s) |
20 (1/s) |
30 (1/s) |
40 (1/s) |
50 (1/s) |
60 (1/s) |
|
|
1 |
43,675 |
43,921 |
44,644 |
45,822 |
47,421 |
51,711 |
57,167 |
63,477 |
70,399 |
|
2 |
43,682 |
43,927 |
44,649 |
45,827 |
47,425 |
51,716 |
57,171 |
63,48 |
70,402 |
|
3 |
81,075 |
81,157 |
81,375 |
81,735 |
82,237 |
83,654 |
85,596 |
88,025 |
90,9 |
|
4 |
275,54 |
275,61 |
275,86 |
276,28 |
276,86 |
278,48 |
280,69 |
283,39 |
286,53 |
|
5 |
342,91 |
343,1 |
343,7 |
344,69 |
346,07 |
349,95 |
355,25 |
361,87 |
369,69 |
|
6 |
343,0 |
343,25 |
343,85 |
344,84 |
346,22 |
350,1 |
355,4 |
362,02 |
369,84 |
|
7 |
395,45 |
395,61 |
396,06 |
396,8 |
397,83 |
400,76 |
404,79 |
409,87 |
415,93 |
|
8 |
395,62 |
395,79 |
396,23 |
396,98 |
398,01 |
400,93 |
404,96 |
410,04 |
416,1 |
|
9 |
406,27 |
406,73 |
408,05 |
410,25 |
413,31 |
421,91 |
433,63 |
448,22 |
456,0 |
|
10 |
413,04 |
413,45 |
414,77 |
416,96 |
420,01 |
428,59 |
440,29 |
452,29 |
465,36 |
В таблице 3 представлены расчеты значения собственных частот колебаний с соответственным учетом вращения для радиального рабочего колеса 10-и лопаток в программе ANSYS WORKBENCH.
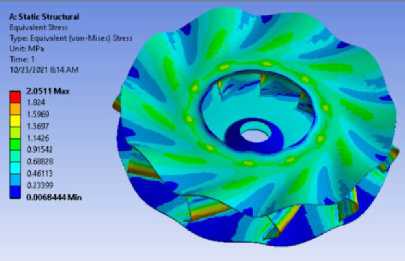
n = 5 (1/s)

n = 10 (1/s)
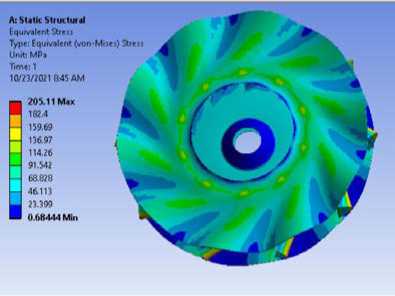
n = 50 (1/s)
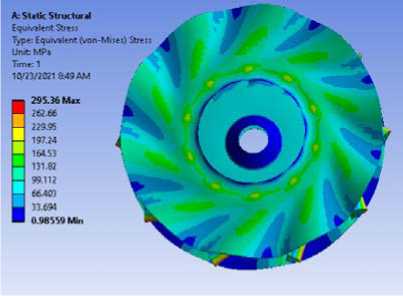
n = 60 (1/s)
Рисунок 4 - Расчеты статического напряжения с учетом вращения радиального рабочего колеса с 10-ю лопатками с помощью программы ANSYS WORKBENCH.
Расчеты собственных частот колебаний для радиального рабочего колеса c 10-ю лопатками представлены в таблице 4 по критерию числа узловых диаметров и узловых окружностей (n / m).
Таблица 4 - Значения собственных частот колебаний для радиального рабочего колеса с 10-ю лопатками в комплексной программе ANSYS WORKBENCH по критерию числового узлового диаметра на числовой узловой окружности.
|
Форма n / m |
Значения собственных частот колебаний в программе ANSYS WORKBENCH, Гц |
||||||||
|
0 (1/s) |
5 (1/s) |
10 (1/s) |
15 (1/s) |
20 (1/s) |
30 (1/s) |
40 (1/s) |
50 (1/s) |
60 (1/s) |
|
|
0/0 |
81,07 |
81,15 |
81,37 |
81,73 |
82,23 |
83,65 |
85,59 |
88,02 |
90,9 |
|
1/0 |
43,67 |
43,92 |
44,64 |
45,82 |
47,42 |
51,71 |
57,16 |
63,47 |
70,39 |
|
1/1 |
395,4 |
395,6 |
396,0 |
396,8 |
397,8 |
400,7 |
404,7 |
409,8 |
415,9 |
|
2/0 |
342,9 |
343,1 |
343,7 |
344,6 |
346,0 |
349,9 |
355,2 |
361,8 |
369,6 |
|
5/0 |
413,0 |
413,4 |
414,7 |
416,9 |
420,0 |
428,5 |
440,2 |
452,2 |
465,3 |
Значения собственных частот для радиального рабочего колеса с 10-ю лопатками в при эксперименте и различных вычислительных программах NISA, FEARS и ANSYS WORKBENCH представлены в таблице 5.
Таблица 5 - Значения собственных частот для радиального рабочего колеса с 10-ю лопатками в эксперименте и различных комплексных программах NISA, FEARS [1] и ANSYS WORKBENCH.
|
n / m |
Комплексная программа |
Значения собственных частот колебаний, Гц от скорости вращения (1/s) |
||||||||
|
0 (1/s) |
5 (1/s) |
10 (1/s) |
15 (1/s) |
20 (1/s) |
30 (1/s) |
40 (1/s) |
50 (1/s) |
60 (1/s) |
||
|
0/0 |
NISA |
98 |
98 |
98 |
98 |
99 |
100 |
102 |
105 |
108 |
|
FEARS |
92 |
92 |
93 |
93 |
94 |
- |
- |
- |
- |
|
|
ANSYS |
81,07 |
81,15 |
81,37 |
81,73 |
82,23 |
83,65 |
85,59 |
88,02 |
90,9 |
|
|
Эксперимент |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
1/0 |
NISA |
45 |
45 |
46 |
46 |
48 |
51 |
56 |
61 |
67 |
|
FEARS |
45 |
46 |
47 |
50 |
53 |
- |
- |
- |
- |
|
|
ANSYS |
43,67 |
43,92 |
44,64 |
45,82 |
47,42 |
51,71 |
57,16 |
63,47 |
70,39 |
|
|
Эксперимент |
44 |
46 |
47 |
49 |
52 |
- |
- |
- |
- |
|
|
2/0 |
NISA |
325 |
325 |
326 |
327 |
328 |
332 |
337 |
343 |
350 |
|
FEARS |
340 |
340 |
341 |
341 |
342 |
345 |
347 |
354 |
362 |
|
|
ANSYS |
342,9 |
343,1 |
343,7 |
344,6 |
346,0 |
349,9 |
355,2 |
361,8 |
369,6 |
|
|
Эксперимент |
341 |
341 |
343 |
344 |
345 |
- |
- |
- |
- |
|
Диаграмма Кэмпбелла показана на рисунке 5, где горизонтальная ось представляет скорость вращения ротора, а вертикальная ось обозначает собственную частоту колебаний. Кривые динамических частот указывают взаимосвязь между собственными частотами и скоростями вращения для каждой формы колебания [10]. В диаграмме анализируются первые 5-ть форм колебаний 1,3,5,7,10.
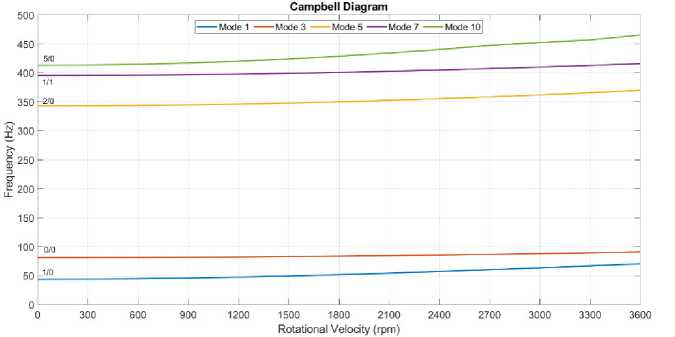
Рисунок 5 - Диаграмма Кэмпбелла для радиальных рабочих колес c 10-ю лопатками
Отмечается, что расчеты собственных частот колебаний для радиального рабочего колеса c 10-ю лопатками в программе ANSYS WORKBENCH дают результаты приближенные к эксперименту для n / m (1/0 и 2/0), которые представлены в таблице 6.
Таблица 6 - Значения собственных частот колебаний с 10-ю лопатками по сравнению к эксперименту в комплексной программе ANSYS WORKBENCH.
|
n / m |
Форма |
Значения собственных частот колебаний, Гц от вращения (1/s) |
||||
|
0 (1/s) |
5 (1/s) |
10 (1/s) |
15 (1/s) |
20 (1/s) |
||
|
1/0 |
№1, расчет |
43,67 |
43,92 |
44,64 |
45,82 |
47,42 |
|
№1, эксперимент |
44 |
46 |
47 |
49 |
52 |
|
|
Отклонение Δf, % |
0,74 |
4,52 |
5,01 |
6,49 |
8,81 |
|
|
2/0 |
№5, расчет |
342,9 |
343,1 |
343,7 |
344,6 |
346,0 |
|
№5, эксперимент |
341 |
342 |
343 |
344 |
345 |
|
|
Отклонение Δf, % |
0,56 |
0,32 |
0,2 |
0,2 |
0,31 |
|
На следующей этапе исследована модель радиального рабочего колеса с валом и 10ю лопатками Pис. 6. Конструкция модели вала с радиальным рабочим колесом 10-и лопаток была жестко закреплена по кольцу вала (см. «1» на Рис. 6а).
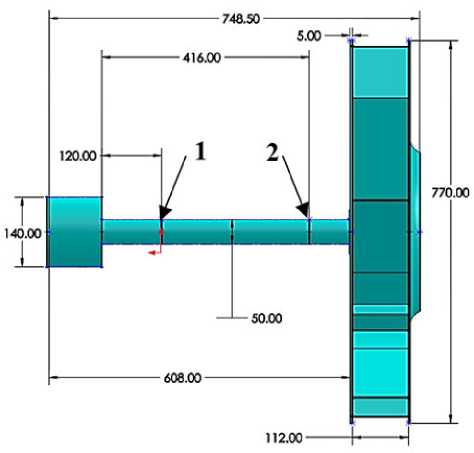
а

б
Рисунок 6 - Модель вала с радиальным рабочим колесом 10-и лопаток (а – общий вид; б – конечноэлементная модель)
На Рис. 7 представлены восемь основных форм колебаний для модели вала с радиальным рабочим колесом с 10-ю лопатками. Каждая форма обладает разнообразной характерной деформацией.
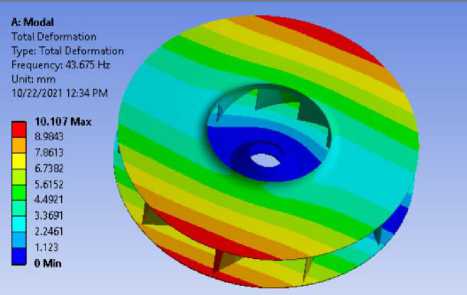
Форма 1
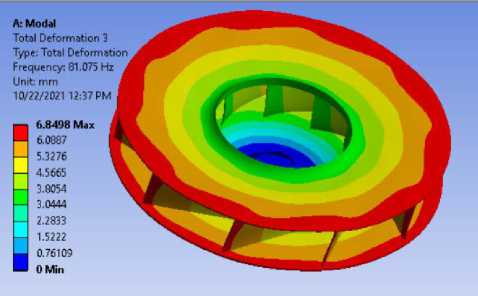
Форма 3
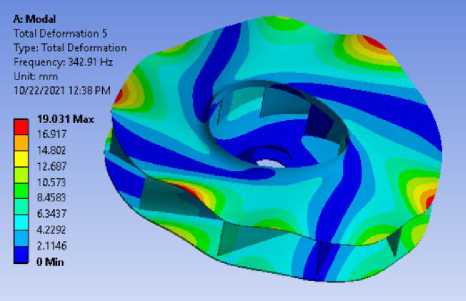
Форма 5
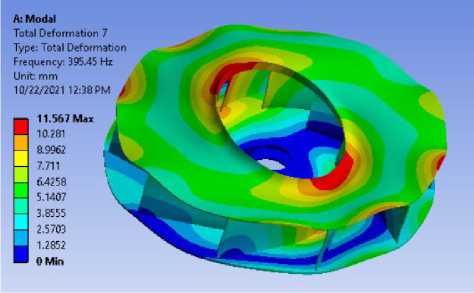
Форма 7
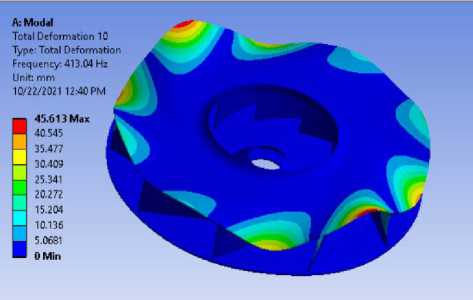
Форма 10
Рисунок 3 - Форма колебаний и собственные частоты колебаний радиальных рабочих колес энергетических турбомашин в программе ANSYS WORKBENCH.
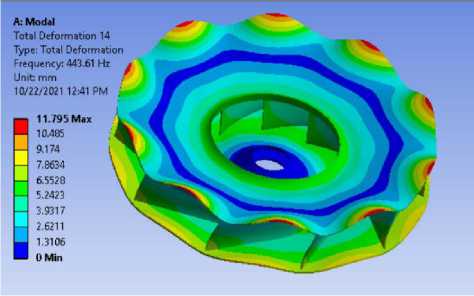
Форма 14

Форма 1
A: Modal
Total Deformation 3 Type: Total Deformat Frequency: 47.963 Hz Unit mm
11/3/2021 9:28 AM
10.442 Max
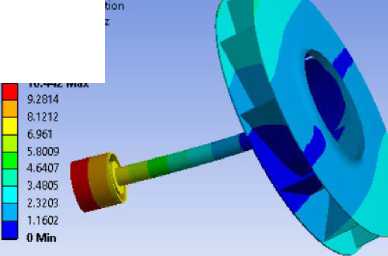

Форма 5
Форма 3
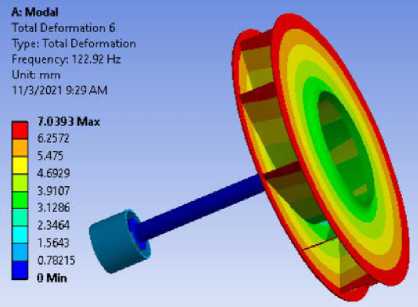
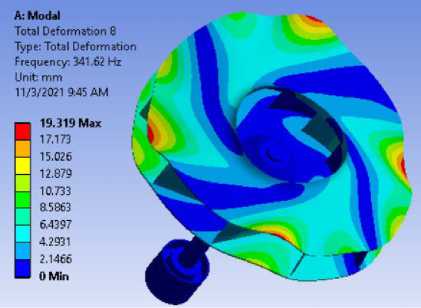
Форма 8
Форма 6

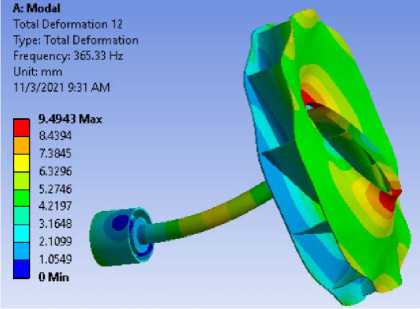
Форма 12
Рисунок 7.- Формы колебаний для модели вала с радиальным рабочим колесом
Форма 10
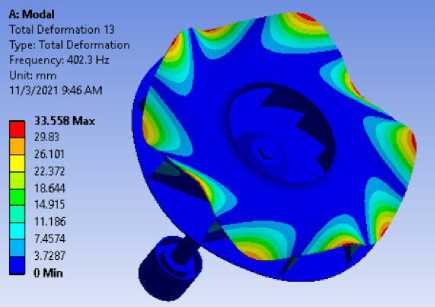
Форма 13
Все значения собственных частот колебаний модели без учета вала для 8-ми основных формах колебания указаны в таблице 7. Кроме значений собственных частот колебаний на
Рис.7 указаны значения деформацией в миллиметрах для 9-и основных форм колебания. Все максимальные значения деформацией представлены в таблице 8. Анализ таблицы 7 показал что, по сранению значения собственных частот колебаний от эксперимента для формы 1 отклоняется на 5,65%, а для формы 8 на 0,18%.
Таблица 7. Значения собственных частот колебаний для этой модели в программе
ANSYS WORKBENCH и BLADIS + .
|
Номер формы |
n / m |
Эксперимент, Гц |
Собственные частоты модели без учета вала, Гц ANSYS (слева) и BLADIS + (справа). |
Максимальные значения деформацией без учета вала, мм |
|
|
5 |
0/0 |
- |
80,263 |
- |
6,9605 |
|
6 |
- |
122,92 |
- |
7,0393 |
|
|
1 |
1/0 |
44 |
41,513 |
- |
9,338 |
|
3 |
- |
47,963 |
- |
10,442 |
|
|
10 |
0/1 |
- |
356,11 |
- |
13,16 |
|
12 |
1/1 |
- |
365,33 |
- |
9,4943 |
|
19 |
- |
425,99 |
- |
11,729 |
|
|
8 |
2/0 |
341 |
341,62 |
349,0 |
19,319 |
|
13 |
5/0 |
- |
402,3 |
402,1 |
33,558 |
Для анализа прочности и надежности радиальных рабочих колес от напряжений и собственных частот колебаний для этой модели в проектировании компрессорного колеса, выполнены численные исследования статического напряженно-деформированного состояния (НДС) при оборотах 5 (1/s), 10 (1/s), 15 (1/s), 20 (1/s), 30 (1/s), 40 (1/s), 50 (1/s), 60 (1/s) в таблице 8.
Таблица 8. Значение статического напряжения σ э с учетом вращения, МПа
|
Скорость вращения вала, (1/s) |
Эксперимент, Мпа |
BLADIS+ (с валом), Мпа |
Максимальные статические напряжения модели, Мпа |
|
5 |
- |
- |
2,0339 |
|
10 |
- |
- |
8,1356 |
|
16 |
- |
- |
18,305 |
|
20 |
32 |
29,94 |
32,542 |
|
30 |
- |
- |
73,220 |
|
40 |
- |
- |
130,17 |
|
50 |
- |
- |
203,39 |
|
60 |
- |
- |
292,88 |
Расчеты собственных частот колебаний для этой модели собраны в таблице 9 по критерию числа узловых диаметров n и узловых окружностей m. В данной таблице представлены значения собственных частот колебаний форм: 1, 6, 8, 10, 12 или (n / m): 1/0, 0/0, 2/0, 0/1, 1/1, 5/0.
Таблица 9. Значения собственных частот колебаний для модели вала с радиальным рабочим колесом и 10-ю лопатками в программе ANSYS WORKBENCH
|
Форма n / m |
Значения собственных частот колебаний в программе ANSYS WORKBENCH, Гц от оборотов вращения (1/s) |
||||||||
|
0 (1/s) |
5 (1/s) |
10 (1/s) |
15 (1/s) |
20 (1/s) |
30 (1/s) |
40 (1/s) |
50 (1/s) |
60 (1/s) |
|
|
0/0 |
123.0 |
123.2 |
123.2 |
123.2 |
123.2 |
123.3 |
123.4 |
360.7 |
368.6 |
|
1/0 |
41.51 |
41.69 |
42.13 |
42.42 |
41.63 |
36.11 |
25.07 |
62.65 |
69.61 |
|
0/1 |
356.1 |
356.1 |
356.3 |
356.5 |
356.9 |
358.2 |
360.5 |
371.8 |
373.9 |
|
1/1 |
365.2 |
365.6 |
365.8 |
366.2 |
366.7 |
368.1 |
369.8 |
430.6 |
432.9 |
|
2/0 |
341.6 |
341.8 |
342.4 |
343.4 |
344.7 |
348.7 |
354.0 |
364.2 |
369.5 |
|
5/0 |
402.3 |
402.7 |
404.1 |
406.3 |
409.4 |
418.1 |
428.6 |
444.7 |
462.0 |
Вывод
Таким образом, в данной работе представлены основные формы колебаний и статических напряжений для модели радиального рабочего колеса c 10-ю лопатками и коротким валом турбомашины для перекачки воздуха в АПК. Также проводились и сравнивались результаты расчета с данными эксперимента и с учетом вращения. Представлены значения собственных частот колебаний для этой модели и его радиального рабочего колеса в различных программах NISA, FEARS и BLADIS+. Отмечается, что расчеты собственных частот колебаний для модели вала и его радиального рабочего колеса c 10-ю лопатками в программе ANSYS WORKBENCH даются призкие результаты к сравнению с экспериментом для n / m равными 1/0 и 2/0. Для модели вала с радиальным рабочим колесом и 10-ю лопатками возникает большой отклик. Собственные частоты резко увеличивают в диапазоне вращения (45...50) 1/s .В конструкции модели нужно рассматривать различные варианты для жестких закреплений по кольцу вала для получения приемлемых для сравнения с экспериментом решений. Представленые кривые динамических частот показывают взаимосвязь между собственными частотами и скоростями вращения для каждой формы колебания в диаграмме Кэмпбелла и могут быть использованы в отстройке от резонансных режимов реальных конструкций радиальных рабочих колес в АПК.
Список литературы Численный анализ собственных частот колебаний и статических напряжений радиальных рабочих колес энергетических турбомашин для АПК
- Irretier H., Repetski O. Vibration and life estimation of rotor structures // The fifth IFToMM. Conference on Rotor Dynamics, Darmstadt. 1998. 7-10 September.
- Yan Y. J., Cui P. L. and Hao H. N. Vibration mechanism of a mistuned bladed disk // Journal of Sound and Vibration. 2008. Vol. 317.P. 294-307.
- Yang M. T. and Griffin J. H. A reduced-order model of mistuning using a subset of nominal system modes // J Eng Gas Turb Power. 2001. Vol. 123. P. 893-900.
- Repetckii O., Ryzhikov I. and Nguyen T. Q. Dynamics analysis in the design of turbomachinery using sensitivity coefficients // Journal of Physics: Conference Series. 2018. 012096.
- Repetckii O., Ryzhikov I. and Springer H. Numerical analysis of rotating flexible blade-disk-shaft systems // Proceedings of the ASME Turbo Expo. 1999.
- До М. Т. Численный анализ влияния расстройки параметров на динамические характеристики рабочих колес турбомашин. - Диссертация кандидата технических наук. Иркутск. 2014. 197 c.
- Whitehead D.S. Effect of mistuning on the vibration of turbomachine blades induced by wakes // Journal of mechanical engineering science. 1966. №. 1. Р. 15-21.
- Castanier M. P., Pierre C. Modeling and Analysis of Mistuned Bladed Disk Vibrations: Status and Engineering Directions // Journal of Propulsion and Powers. 2006. №. 2 (122). Р. 384-396.
- Ewins D. J. Vibration characteristics of Bladed disc assemblies // Journal of Machanical Engineering Science. 1973. №. 5 (12). Р. 165-186.
- Campbell W. The protection of Steam Turbine Disk Wheels from Axial Vibrations // Trans. of the ASME 46. 1924. Р. 31-160.


