Численный анализ влияния потоков утечек на процессы течения и теплообмена в условиях пластицирующей экструзии

В процессе пластицирующей экструзии в винтовых каналах шнековых машин движение нелинейных полимерных сред и теплообмен сопровождаются фазовым переходом, внутренней диссипацией, вынужденной конвекцией, изменяющейся геометрией канала, потоком утечек через зазор между гребнем нарезки червяка и внутренней поверхностью корпуса (Рис. 1 а ) [1, 2]. Изменение размера зазора существенно влияет на процессы тепломассообмена в канале и, как следствие, на эксплуатационные характеристики экструзионного оборудования. В конце 50-х годов прошлого столетия первые экспериментальные исследования процессов течения и теплообмена в винтовых каналах экструдеров явились основанием для начала интенсивного теоретического анализа процесса экструзии. За минувшие десятилетия предложены различные подходы и математические модели, описывающие процессы тепломассопереноса, в том числе с учетом потоков утечек расплава полимера через гребни винта.

Мор и Маллок [3], рассматривая изотермическое течение ньютоновской жидкости через плоскость, нормальную к оси червяка (Рис. 1 б ), впервые предложили подход для определения потока утечек через зазор над гребнем шнека. Ими выведено аналитическое выражение, позволяющее находить величину утечек и оценить их влияние на работу экструдера в режиме заданного градиента давления и на градиент давления в режиме заданного расхода. Однако модель [3] имеет существенные недостатки: она не соотносит перепады давления в канале шнека и зазоре с величиной потока утечек, не отражает аномальность жидкости, неизотермичность процесса и расход расплава полимера над гребнем в направлении координаты z (Рис. 1 б ).

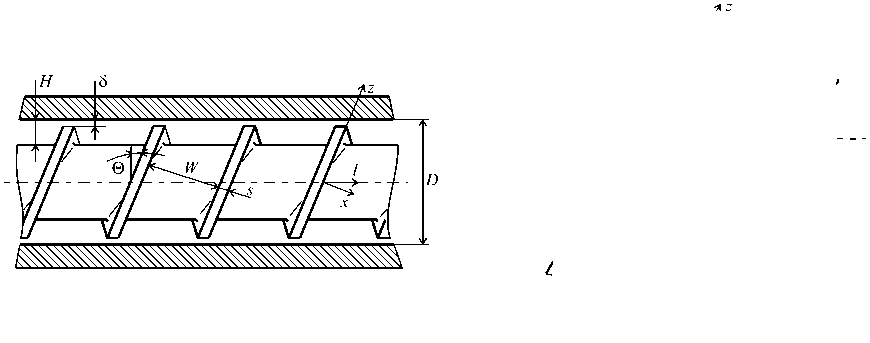
Рис. 1. Схема винтового канала экструдера ( а ) и его развертка на плоскость ( б ): D – внутренний диаметр цилиндра; H и W – высота и ширина канала; s – ширина гребня нарезки червяка; δ – величина зазора; V ₀ – окружная скорость шнека; Θ – угол нарезки винтовой линии; l – ось червяка

Существенное развитие модель [3] получила в работах [4–6], где авторами учтено влияние перепада давления в зазоре в направлении оси x . Но, по-прежнему, остался открытым вопрос об учете аномалии вязкости, потока жидкости над гребнем червяка вдоль оси z и тепловыделения в зазоре. В работах [7–9]

предложена математическая модель, описывающая аномалию вязкости материала и изменение расхода утечек по длине канала в одномерном случае.

Для дозирующей зоны пластицирующего экструдера в [10, 11] рассмотрена квазитрехмерная математическая модель неизотермического течения аномально-вязкой жидкости. На входе в канал задавалась температура полимера, заведомо большая температуры плавления. Шнек считался адиабатической поверхностью. В [10] проведено сравнение данных численных и экспериментальных исследований давления, температуры и энергетических затрат, в том числе для канала с радиальным зазором. Отмечено существенное различие между результатами расчетов и экспериментов при больших значениях расходов. В [11] использован аналогичный [10] подход, с помощью которого анализировалось влияние величин зазора и диаметра шнека на процессы тепломассообмена. В работе сделан вывод о том, что при зазоре, не превышающем 0,003 диаметра шнека, влияние утечек на параметры течения в винтовом канале практически не сказывается. В противном случае характеристики течения могут отличаться существенно.

Нужно отметить, что все упомянутые выше модели отвечали процессам течения в шнековых насосах [4–9] или в зоне дозирования пластицирующего экструдера [10, 11]. Имеющиеся на сегодняшний день математические модели зоны плавления, как правило, одномерные, что не позволяет учитывать утечки через зазор в условиях фазового перехода полимерного материала и неоднородности температурного поля в винтовом канале.

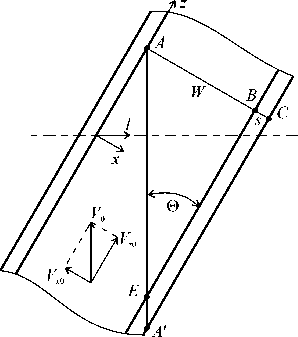
В данной статье решение общей задачи течения и плавления полимера в канале экструдера осуществляется с учетом радиальных зазоров и теплообмена в шнеке. При построении математической модели процессов движения и теплообмена полимера в условиях фазового перехода в винтовом канале пластицирующего экструдера вводятся следующие упрощения: процесс

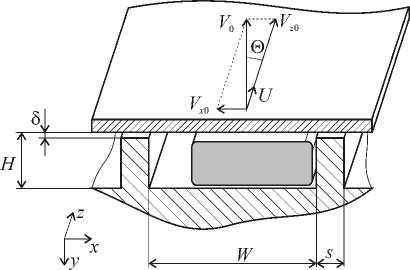
Рис. 2. Схема развернутого винтового канала

считается стационарным и с постоянным массовым расходом; винтовой канал разворачивается на плоскость (Рис. 2), используется обращенное движение; перенос тепла вдоль канала происходит в основном за счет конвективной составляющей, поэтому диффузия тепла по координате z в расчет не принимается; упругие процессы в расплаве полимера не рассматриваются; градиенты составляющих скорости в направлении оси z отбрасываются, поскольку геометрия канала постоянна (или изменяется очень плавно) по длине, которая на два-три порядка больше высоты и ширины, к тому же массовые силы малы по сравнению с силами вязкого трения.

В результате допущений система дифференциальных уравнений, описывающая движение и теплообмен полимера в канале червяка и полученная на основании законов сохранения массы, количества движения и энергии [1, 2], будет иметь вид:

8 v_x ⁸ v y

—- + —- = 0,

8x

8 (   8vrI  5 (   (8vr  8v-))8

2—I ц_э —- 1+    ц_э I —- + —-I = —,

8x V   8x J  8y I   (5y   8x J J з 8

2 I Ц

8 y V

8v ।   8 (   (8vr   8v  ] |8

I+ ц_э I —- x + — ^y I = — ,

8y J  8x V  V 8y   8x J J8

8 (   8 v₇ I   8 (   8 v₇ I 8 P

I цэ I +I цэ       I =

8 x V ³ 8 x J 8 y V ³ 8 y J 8 z

(_ 8T    8T 8TI   8 (, 8TI  8 (, 8TI р CI v, — + v. — + v    I = —IX— I+--1^— I + ЦЭ 2,

V 8z     8x   y 8y J  8x V  8x J  8y V  8y J2

где v_x , v_y , v_z — компоненты вектора скорости течения расплава полимера в канале; P — давление в канале; 1 ₂ — второй инвариант тензора скоростей деформации; ц _Э — эффективная вязкость расплава полимера; v_z — среднеинтегральное значение скорости v_z в текущем по длине поперечном сечении канала; T — температура; р , C, X — плотность, удельная теплоемкость, коэффициент теплопроводности полимера, являющиеся функциями температуры. Здесь эффективная вязкость определяется как

Ц э =Ц о exp ( - ₽ ( T - T ,) ) ( 1 2 /2)⁽ n ^{- 1)/}2 ,

где в — температурный коэффициент вязкости; n — показатель аномалии вязкости расплава полимера; ц₀ — коэффициент консистенции расплава полимера при температуре T ₀. Второй инвариант в уравнениях (5), (6) вычисляется по формуле:

4 п ( 8 vx)    I 8vy I I 8vx   8vy I    (8vz)( 8

• 2     x ^yx^yz z

  ---= 2 ----- + I ----- I + I--1--I + ----- + I -----

• 2    V 8х J l8y)    ^8y   8x )   V 8x J(8

• V^J

Для твердой фазы уравнение энергии (5) преобразуется к виду ( U — скорость твердой фазы):

_ 8 T 8 (.8 T I 8 (.8 T I C р U— = —I X — I+—I X — I .

8 z    8 x V 8 x J 8 y V 8 y J

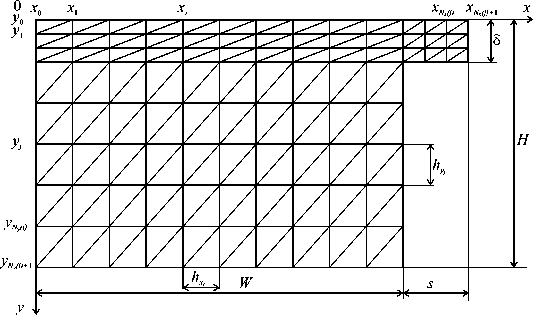
Рис. 3. Дискретное представление поперечного сечения канала

Уравнения движения и уравнение несжимаемости решаются методом конечных элементов в естественных переменных с использованием метода Галеркина [12–14]. Компоненты скорости аппроксимируются квадратичными, а давление — линейными полиномами на треугольном элементе (Рис. 3).

При выборе метода решения уравнения энергии учитывается следующее: длина канала пластицирующего экструдера много больше ширины и высоты; температурная задача существенно нелинейная; полимерный материал при его продвижении вдоль канала претерпевает фазовое превращение (полимер переходит из твердого состояния в расплавленное). Согласно [15, 16] наиболее приемлемым методом решения уравнения энергии является маршевая схема метода конечных разностей с записью конвективных членов против потока. Для представления поперечного сечения канала в дискретном виде используется сетка с переменным шагом. Узлы конечно-разностной сетки совпадают с узлами сетки из конечных элементов (Рис. 3).

Для решения задачи учета потока утечек в математической модели пластицирующего экструдера в зонах плавления и дозирования [17–20] применяется подход, предложенный Мором и Маллоком [3] и представленный на рисунке 1 б . Тогда массовый расход через сечение плоскостью, нормальной к оси червяка (на рисунке 1 б линия AA ′ , на рисунке 4 а — замкнутая область 1 ), будет равен заданному массовому расходу G ₀ , [кг/с]. Это справедливо для любого сечения по длине канала шнека при его работе в стационарном режиме.

Производительность шнекового экструдера в некотором произвольном сечении с учетом расхода расплава полимера через радиальный зазор можно определить по формуле:

G 0 = G z - G u ,                                             (7)

где G_z — массовый расход в направлении оси z (на рисунке 4 а — расход через замкнутую область 2 ); G_u — массовый расход утечек (на рисунке 4 а — расход через замкнутую область 3 ). Массовый расход через замкнутую область 2 складывается из расходов в канале и зазоре и составляет

WH                      W + s δ

G_z = ∫∫ ρ ( x , y ) v_z ( x , y ) dxdy + ∫∫ ρ ( x , y ) v_z ( x , y ) dxdy , 00                       W 0

где ρ ( x , y ) — плотность полимерного материала; W и s — ширина канала и гребня нарезки, соответственно; v_z ( x , y ) — составляющая скорости течения жидкости в канале.

Расход в канале в пределах зоны плавления зависит от расходов твердой фазы и расплава полимера. Здесь поле скоростей v_x ( x , y ) с учетом потока утечек находится по заданному перепаду давления ∆ P_AC (перепад давления между точками A и C , см. Рис. 4). Массовый расход утечек вычисляется по формуле:

=           x

G_u =ρ _m         v_x ( x _{x = W + s} , y ) dy .

tg Θ ₀

Следует отметить, что расход утечек G_u может быть получен и при любых других значениях координаты x в диапазоне от 0 до W + s .

Поскольку на рисунках 1 б и 4 точка A ′ — это та же самая физическая точка A , то перепады давления между ними и точкой C одинаковы: ∆ P_AC = ∆ P_{A ′ C} . Тогда

∆ P AC

= ∆ P_{A ′ C}

W+s∂P ⋅ tg Θ∂z

где ∂ P ∂ z — компонента градиента давления в канале в направлении координаты z . Будем считать, что при численном определении расхода утечек на текущей длине по координате z компонента градиента давления ∂ P ∂ z в интервале от A ′ до C есть величина постоянная и изменяется скачком при переходе к следующему значению z .

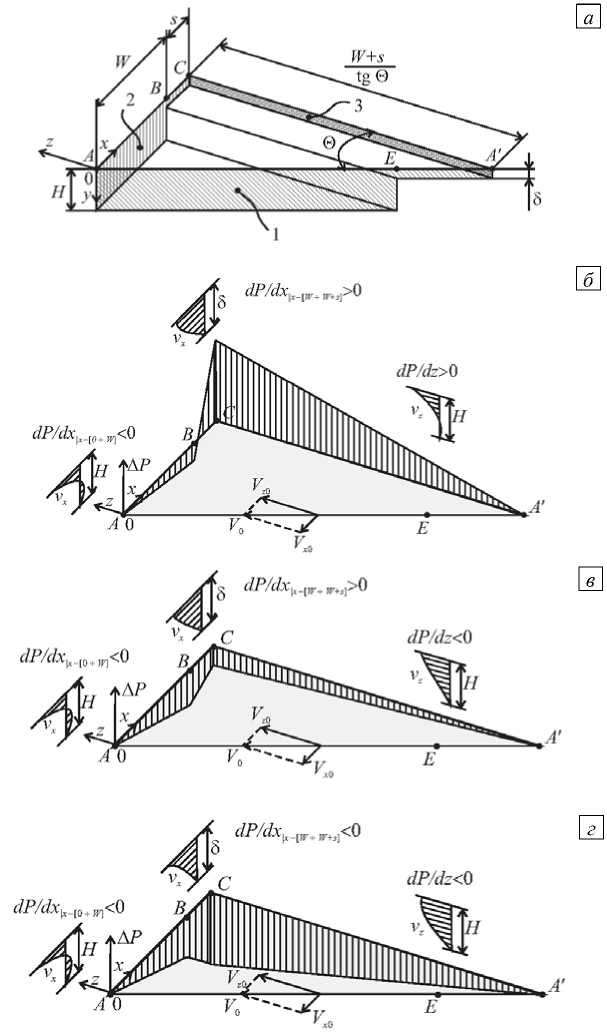
Рис. 4. Замкнутый объем канала для расчета утечек ( а ), распределение давления по треугольнику ACA' и эпюры скоростей в канале и зазоре ( б – г )

Рассмотрим характерные режимы работы экструдера в зоне дозирования и проследим динамику изменения расхода утечек от величины градиента давления д ?( д z (Рис. 4 б - г ). При работе экструдера в режиме заданного перепада давления геометрические размеры его элементов — глубина канала H и величина зазора 5 , обуславливают соответствующие течения с положительным или отрицательным градиентом давления д?/д z , например д?!д z >  0 на рисунке 4 б . Перепад давления N P AC , рассчитанный по формуле (8), также положителен. Для этого режима работы компонента градиента давления в зазоре положительна: д Р/ д Х|_х = W ₊₍ W _{+ $} ^ >  0 при отрицательном значении д ?! д х ^ =[ _{0 +} W ] в канале (Рис. 4 б) . Поскольку глубина канала H много больше величины зазора 5 , то компонента градиента давления в канале д?!д х всегда имеет отрицательное значение (Рис. 4 б - г ). При отрицательном значении д Р/ д z компонента градиента давления в зазоре д?!д Х| _х = W ₊₍ W _{+ $} ) ] может быть положительной (Рис. 4 в ), нулевой (на рисунке 4 не представлена) или отрицательной (Рис. 4 г ). Наибольший расход утечек имеет место в случае, показанном на рисунке 4 б .

Для реализации задачи тепломассопереноса в канале пластицирующего экструдера с учетом потока утечек через зазор при заданном массовом расходе G ₀ на каждом шаге по длине канала организуется итерационная процедура. На последующем шаге в качестве массового расхода утечек используется его величина с предыдущего шага ( G_u ) или задается некоторое первоначальное приближение. Итерационная процедура состоит из последовательно выполняемых действий:

• –    из решения методом конечных элементов уравнения движения (4) при известном массовом расходе в направлении оси z , равном (см. (7)) G_z = G 0 + G u , определяется поле скорости v_z и компонента градиента давления d Р /д z . По формуле (8) вычисляется перепад давления A P AC , далее по выражениям (1)–(3) находятся компоненты скорости v_x , v_y и давление P в поперечном сечении канала;

• -    по распределению компоненты скорости v_x рассчитывается новое значение расхода утечек G , . Если относительная невязка между предыдущим расходом утечек G u и вновь вычисленным G U по абсолютной величине превышает некоторую наперед заданную малую величину, то данная итерационная процедура продолжается до тех пор, пока не выполнится условие по точности;

• –    на основании установленных поля скорости из решения уравнения энергии (5) определяется поле температур в узлах сетки на текущем шаге по длине канала;

• –    исходя из нового распределения температуры перевычисляются поля скоростей и расход потока утечек.

Как показали результаты численных экспериментов, сходимость итерационного процесса достаточно оценивать по компоненте скорости vx , поскольку сходимость по другим компонентам скорости и температуре удовлетворяется также. Если в каждом узле относительная разность скорости не превышает по модулю некоторой наперед заданной малой величины б v m+1 - v m xx — б , V Vx0

то считается, что итерационная процедура сходится. Далее осуществляется переход к следующему шагу по длине канала, и процедура повторяется.

Представленный подход к определению потока утечек через зазор учитывает вынужденную и напорную составляющие течения расплава полимера, аномально-вязкие свойства среды, неоднородность температурного поля в поперечном сечении канала и зазоре. Созданная на его основе методика определения потока утечек через зазор между гребнем нарезки червяка и внутренней поверхностью корпуса может использоваться в математических моделях (одно-, двух или трехмерных) течений жидкости в винтовых каналах простых шнековых насосов и пластицирующих экструдеров как для зоны дозирования, так и для зоны плавления.

Вычислительные эксперименты по изучению влияния утечек на характеристики пластицирующего экструдера с классическим шнеком, размеры которого приведены в таблице 1, выполнены с помощью математической модели, представленной в работах [18–20]. Исследуемым материалом служил полиэтилен (ПЭ), реологические и теплофизические свойства которого показаны в таблице 2 и на рисунке 5. Индекс sl в таблице 2 соответствует твердому состоянию полимера, а m — расплавленному. Температура плавления полиэтилена обозначается как T_m ; эффективная вязкость расплава ПЭ определяется по формуле (6).

Таблица 1. Базовая геометрия классического шнека

Внутренний диаметр цилиндра (корпуса), мм	160,0
Наружный диаметр шнека, мм	159,4
Шаг винтовой нарезки, мм	160,0
Ширина канала W , мм	137,3
Ширина гребня винтовой нарезки s , мм	15,3
Длины геометрических зон загрузки, сжатия и дозирования A Z 1 / A Z 2 / A Z 3 , число витков	10/10/7
Суммарная длина шнека Z К , число витков	27
Глубина канала в зоне загрузки, H 1 , мм	16
Глубина канала в зоне дозирования H 2 , мм	4
Угол подъема винтовой линии ®	17039,
Радиальный зазор между гребнем шнека и корпусом S , мм	0,3
Диаметр отверстия в шнеке, мм	48

Таблица 2. Реологические и теплофизические свойства полиэтилена

Исследуемый материал	n	^ 0	т T 0	в	т m	Р sl	Р m	X sl	X m
	–	Па-с n	°С	1/°С	°С	кг/м3		Вт/(м^°С)
ПЭ	0,44	10825	160	0,018	110	919,0	779,0	0,335	0,182

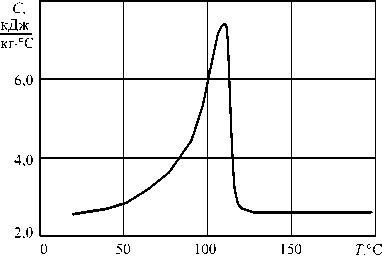
Рис. 5. Зависимость удельной теплоемкости ПЭ от температуры

Температура цилиндра экструдера T_b задавалась равной 200 ° С, температура в шнеке рассчитывалась по модели из [19]. При этом на внутренней поверхности отверстия, которое предусматривает конструкция шнека, задавались адиабатические условия. Начальная температура гранулята T_z 0 составляла 20 ° С, число оборотов шнека — N = 60 об/мин. Массовая производительность экструдера G ₀ изменялась от 0,02

до 0,12 кг/с.

Поскольку в процессе эксплуатации оборудования величина радиального зазора между гребнем шнека и внутренней поверхностью цилиндра изменяется, то интерес представляла оценка влияния величины зазора на рабочие характеристики экструдера.

Вычислительный эксперимент проведен для двух значений зазоров 5 : 0,3 и 0,6 мм. Число разбиений задавалось равным 20 — по высоте канала (три приходились на зазор), 40 — по ширине канала. Численные исследования показали, что измельчение сетки в зазоре изменяет результаты расчета не более чем на 3%.

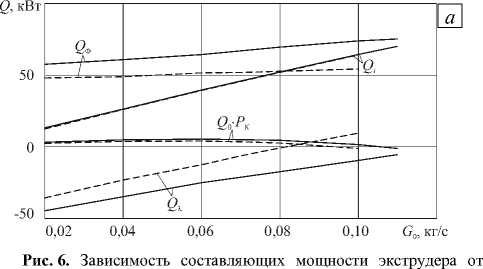
На рисунке 6а приведены зависимости составляющих мощности пластицирующего экструдера от его производительности G0 при различных радиальных зазорах между гребнем нарезки червяка и внутренней поверхностью цилиндра. Здесь: Q0PК — мощность, затрачиваемая на перенос массы среды по каналу экструдера; Q0 — объемный расход полимера; PК — перепад давления между выходом и входом TСр.Вых экструдера; Qi = G0 J C(T)dT — изменение внутренней энергии полимерного материала при его Tz0

продвижении от входа к выходу канала в единицу времени; Qф — суммарная мощность диссипативного источника тепла; QX — суммарная мощность подводимой (отводимой) через стенки канала тепловой энергии. Из рисунка видно, что увеличение зазора наиболее сильно влияет на мощность диссипации механической энергии Qo в канале экструдера и мощность подводимой (отводимой) тепловой энергии QX. Поскольку мощность на валу электродвигателя NДв определяется суммой Qo и Q0РК , то и NДв снижается с увеличением величины зазора.

На рисунке 6 б показаны зависимости средней ( T _Ср ) и максимальной ( T _max ) температур расплава на выходе из экструдера от производительности и величины зазора. При увеличении зазора происходит снижение как средней, так и максимальной температуры расплава полимера на выходе из канала, что обусловлено снижением интенсивности диссипативного источника тепла Q _ф . Снижение максимальной температуры при увеличении зазора 5 от 0,3 до 0,6 мм во всем диапазоне изменения расхода не превышает 4 ° С, средней — 3 ° С.

температуры T _Ср на

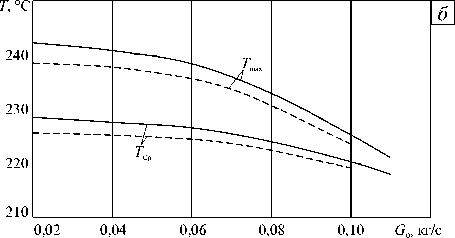
( а ) и зависимость средней расхода G ₀ при различных

его производительности G ₀

выходе из экструдера и максимальной температуры Tmax от массового значениях радиального зазора 5 , мм: 0,3 (сплошная линия); 0,6 (штриховая)

а

224,9

б

222,8

220,6

218,4

216,3

214,1

211,9

209,8

207,6

205,4

203,3

201,1

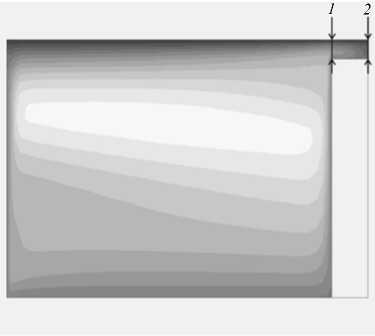
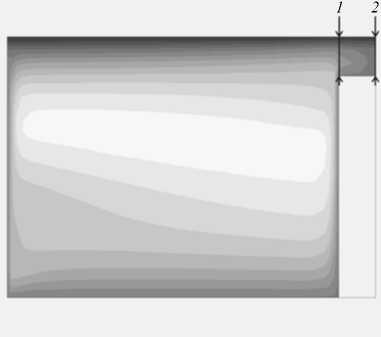
Рис. 7. Температурное поле в поперечном сечении канала на выходе из экструдера при различных значениях 8 , мм: 0,3 ( а ); 0,6 ( б )

На рисунке 7 изображены температурные поля в поперечном сечении зоны дозирования канала для рассматриваемых величин радиальных зазоров при массовом расходе G 0 = 0,09 кг/с. Изменение температуры расплава в сечениях зазора 1 и 2 , изображено на рисунке 8. Можно видеть, что максимальная температура полимера в канале с меньшим зазором выше и превосходит температуру корпуса на 28 ° С (Рис. 7 а ), в то же время максимальная температура непосредственно в зазоре над гребнем шнека (Рис. 8 а ) превышает температуру корпуса лишь на 15 ° С. Это связано с тем, что, несмотря на значительные по величине скорости сдвига, наблюдающиеся в этой части канала, энергия, выделившаяся за счет вязкого трения, эффективно отводится через изотермическую поверхность цилиндрического корпуса и шнека экструдера в силу малой величины зазора.

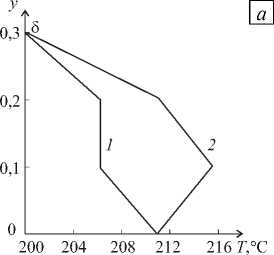
Рис. 8. Зависимость температуры по высоте зазора (сечения 1 и 2 ) при 8 = 0,3 мм ( а ) и 8 = 0,6 мм ( б )

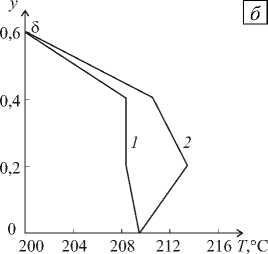
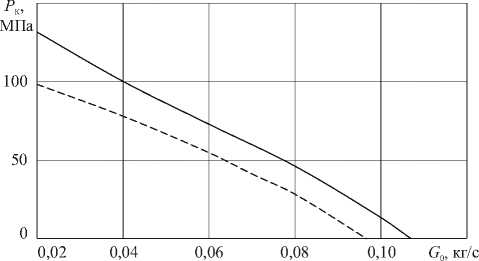
Рис. 9. Напорно-расходные характеристики экструдера при различных радиальных зазорах 8 , мм: 0,3 (сплошная линия); 0,6 (штриховая)

Зависимости перепада давления    PК от производительности экструдера    G0

и радиальных зазоров 8 приведены на рисунке 9. Полученные       результаты       расчетов свидетельствуют, что увеличение зазора оказывает значительное влияние на изменение напорнорасходных   характеристик   пластицирующего экструдера. Увеличение    зазора между шнеком и внутренней поверхностью цилиндра приводит к снижению производительности, что в первую очередь обусловлено увеличением потока утечек через зазор. При открытом выходе (РК = 0) увеличение зазора 8 с 0,3 мм до 0,6 мм приводит к снижению массового расхода G0 на 10%.

Выводы

Разработана квазитрехмерная математическая модель пластицирующей экструзии нелинейных полимерных сред в винтовых каналах шнекового оборудования с учетом утечек через зазор между гребнем нарезки червяка и внутренней поверхностью корпуса в зонах плавления и дозирования. Предложенная методика определения потока утечек, базирующаяся на законе сохранения масс, позволяет описывать изменяющуюся геометрию канала, диссипацию тепла в зазоре, нелинейный характер поведения расплава полимера, перепад давления в канале шнека как в продольном, так и в поперечном направлениях, неоднородность температурного поля в канале шнека и зазоре, в том числе и в условиях фазового перехода. В результате численных исследований процесса пластицирующей экструзии установлено, что увеличение зазора между гребнем нарезки червяка и внутренней поверхностью корпуса приводит не только к снижению производительности экструдера, но также к уменьшению средней и максимальной температуры расплава полимера на выходе из экструдера за счет снижения диссипации тепла.

Работа выполнена при финансовой поддержке РФФИ (проект № 13-08-96034-p_урал_а).