Численный анализ влияния поверхностного трения на аэродинамические характеристики профиля
Автор: Терехин Александр Александрович, Сидельников Рудольф Васильевич, Терехина Татьяна Валерьевна
Рубрика: Расчет и конструирование
Статья в выпуске: 10 (110), 2008 года.
Бесплатный доступ
Исследуется влияние точности моделирования пограничного слоя на точность вычисления интегральных и распределённых характеристик профиля крыла на примере RAE 2822. Используются две математических модели течения газа: k-ω SST и «невязкого» газа. Решение проводится алгоритмами первого и второго порядков точности, которые дают разные результаты в области отрыва пограничного слоя. Как показали численные исследования, точность расчёта коэффициента трения на поверхности профиля и толщины пограничного слоя существенно влияет на определение точки отрыва потока, что сказывается на вычислении распределенного по поверхности давления и интегральных характеристик профиля.
Короткий адрес: https://sciup.org/147151429
IDR: 147151429 | УДК: 533.6.011:51
Текст научной статьи Численный анализ влияния поверхностного трения на аэродинамические характеристики профиля
Турбулентные отрывные течения играют важную роль в современной аэродинамике в связи с необходимостью анализа нестандартных условий полета и решения ряда других проблем, неразрывно связанных с явлением отрыва потока от обтекаемой поверхности. Сложность моделирования отрывных течений объясняется их физическими особенностями, параметры которых определяются конкретными геометрическими характеристиками рассматриваемого течения и граничными условиями, что делает построение универсальной полуэмпирической модели турбулентности для расчета отрывных течений исключительно сложным. Известно, что численное моделирование отрывных течений может быть выполнено на базе различных моделей турбулентности и даже на модели идеальной жидкости, где эффекты диссипации энергии создаёт численная диффузия. Так же неоднократно в литературе отмечалось, что за счёт численной диффузии можно моделировать эффекты турбулентности, при этом улучшая сходимость и устойчивость математического счёта [1-3].
Положение точек отрыва и присоединения пограничного слоя (ПС) характеризуется поверхностным трением, которое при численном моделировании является результатом совместного решения полуэмпирической модели турбулентности и соответствующей ей модели стенки. Неточное определение точек отрыва ведёт к искажению описания распределения давления по поверхности исследуемого объекта, что означает неизбежное ошибочное определение интегральных характеристик. В данной статье с целью отработки моделей турбулентности проводится оценка влияния точности определения коэффициента поверхностного трения Cf на распределение давления и расчётные интегральные аэродинамические характеристики (подъёмную силу и центр давления) путём сравнения с результатами обширного физического эксперимента для случая обтекания профиля RAE 2822.
Сверхкритический профиль RAE 2822 имеет особенности, связанные с большой кривизной хвостовой части. Подробное его описание приводится в работе [4]. В ней вариант обтекания №1 соответствует безотрывному течению с отсутствием на поверхности профиля скачков уплотнения. Вариант обтекания №10 является наиболее сложным из всех случаев, представленных в работе [4], там скачок уплотнения, образующийся на верхней поверхности профиля, вызывает развитый отрыв пограничного слоя [5].
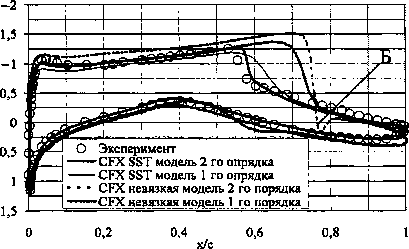
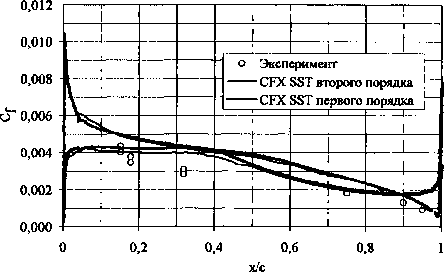
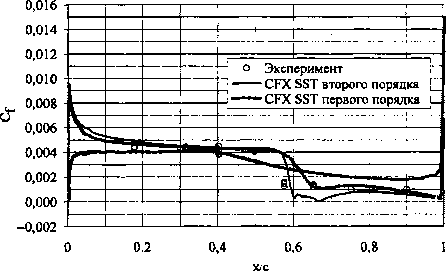
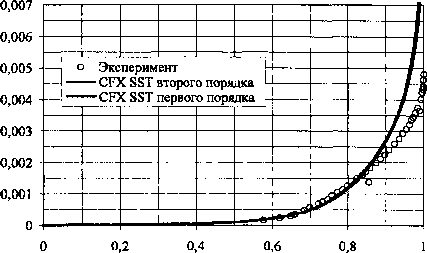
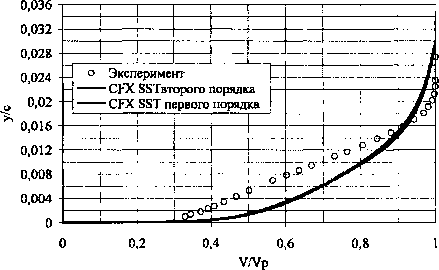
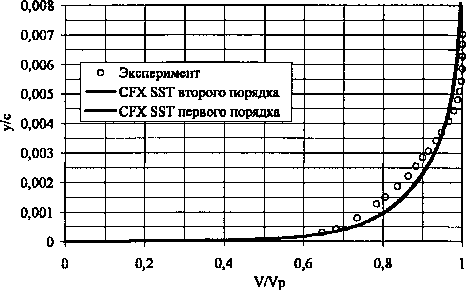
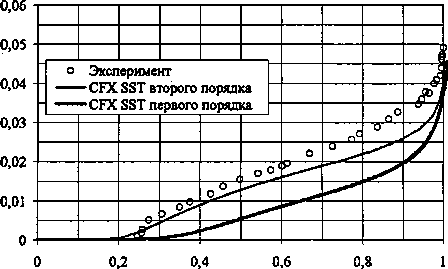
Исходные данные для постановки численного эксперимента представлены в табл. 1. Анализ положительных и отрицательных качеств моделей течений проводится на модели вязкого газа с полуэмпирической моделью турбулентности k- В расчётах используется «С» сетка, основанная на «Неха» элементах. Параметр Y+ по поверхности профиля для модели k-ю SST не превышает 1, в соответствии с чем, количество контрольных объёмов в расчётной области для k-co SST модели турбулентности составляет 40 194. Для модели «невязкого» газа из-за увеличения размера грани контрольного объёма в 103 раз по Расчет и конструирование направлению нормали к поверхности профиля, размер сетки составляет 26 930 контрольных объёмов. В качестве характерных параметров для анализа эффективности моделей выбраны: • распределение коэффициента давления с г2(р-р„) Р р»Х ’ • распределение коэффициента поверхно- P=VM Таблица 1 Исходные данные численного эксперимента Вариант 1 10 мю 0,676 0,750 а, град 2,400 3,190 Re, 106 5,700 6,200 Длина профиля, м 0,389 • профиль скорости V, отнесенный к скорости на границе пограничного слоя Vp. На рисунках ниже обозначены: координата у - расстояние по нормали от поверхности профиля, х — расстояние от носка профиля, с - длина профиля. Интегральные характеристики сравниваются по коэффициентам нормальной силы Сп и центра давления Cd. Одной из характерных особенностей модели «невязкого» газа является появление в решениях флуктуаций давления нефизической природы. Решение уравнений «невязкого» газа схемами первого порядка точности даёт флуктуацию давления в дозвуковой области, близкой к трансзвуковой (рис. 1, область А). 0,0 0,2 0,8 1,0 Рис. 2. Распределение коэффициента давления по поверхности профиля, вариант 10 Рис. 1. Распределение коэффициента давления по поверхности профиля, вариант 1 В случае решения уравнений «невязкого» газа с помощью схемы второго порядка точности, флуктуации давления на поверхности профиля наблюдаются в области за скачком уплотнения (рис. 2, область Б). За счёт повышенной численной диффузии (при использовании алгоритма первого порядка точности для уравнений «невязкого» газа) происходит сглаживание флуктуаций давления, что соответствует более точному описанию процесса трансзвукового обтекания (см. рис. 2). Как показали расчёты, при дозвуковых скоростях безотрывного обтекания в численной модели пограничный слой мало влияет на определение коэффициента давления. Несоответствие значения коэффициента трения на поверхности при численном расчёте с физическим экспериментом (рис. 3, 4) не приводит к расхождению коэффициента давления (см. рис. 1). Рис. 3. Распределение коэффициента поверхностного трения, вариант 1 Рис. 4. Распределение коэффициента поверхностного трения, вариант 10 Терехин А.А., Сидельников Р.В., Численный анализ влияния поверхностного трения Терехина Т.В.__________________________________на аэродинамические характеристики профиля Завышение поверхностного трения приводит к ошибке определения толщины пограничного слоя в среднем на 40% (рис. 5, 6). Здесь расхождения связаны с особенностями численного эксперимента (численная диффузия, разрешающая способность разностной сетки, сгущение сетки к поверхности и т. д.) (табл. 2), а качественная же картина моделируется достаточно надежно всеми математическими моделями. Таблица 2 Сравнение интегральных характеристик Эксперимент k-ш SST Модель «невязкого» газа Расхождение между экспериментом и k- Расхождение между k-со SST и моделью «невязкого» газа, % Расхождение между экспериментом и моделью «невязкого» газа, % Вариант 1 сп 0,566 0,5929(0,5681) 0,7318(0,6212) 4,7(0,37) 23,4 (4,7) 29,2 (9,7) т2 — 0,2299 (0,2263) 0,2874 (0,2634) -(1,56) 25,0 (14,5) — cd 0,3870 (0,3978) 0,3923 (0,4240) - (2,79) 1,3 (9,5) — Вариант 10 Сп 0,743 0,7586 (0,7390) 1,0553 (0,9255) 2,1(0,53) 39,1 (22,0) 42,0 (24,5) mz — 0,2860 (0,2892) 0,4481 (0,3937) -(1,14) 56,0 (37,6) — Cd — 0,3759 (0,3907) 0,4237 (0,4249) -(1,48) 12,7(13,0) — В скобках приведены значения интегральных характеристик, полученные с алгоритмом первого порядка точности. При образовании скачка уплотнения на поверхности и его взаимодействии с пограничным слоем наблюдается отрыв последнего. Область, где коэффициент поверхностного трения близок к нулю (см. рис. 4), соответствует отрыву и прилипанию ПС. В данном случае различные модели ведут себя по-разному. Лишь одна модель k-® SST с использованием алгоритма второго порядка точности корректно моделирует отрыв ПС и соответствует физическому эксперименту. В областях течения до отрыва ПС решения для Ср разными схемами дают одинаковые результаты, но существенно отличаются после отрыва. V/Vp Рис. 5. Распределение скорости по толщине пограничного слоя на верхней поверхности профиля, вариант 1, х/с=0,319 Рис. 6. Распределение скорости по толщине пограничного слоя на верхней поверхности профиля, вариант 1, х/с=0,95 Наряду с использованием Cf, взаимодействие ПС с обтекаемой поверхностью можно оценить по характеру изменения профиля скорости в пристеночной области ПС (рис. 7, 8). Профили скорости при моделировании обтекания профиля крыла без образования скачка уплотнения для моделей k-to SST по разным схемам совпадают (см. рис. 5-7). Это подтверждает то, что в дозвуковой области могут быть использованы более простые схемы решения систем уравнений. А в варианте обтекания с отрывом пограничного слоя профили скорости до скачка уплотнения и после, полученные схемами разного порядка точности с использованием модели k-® SST, отличаются значительно (см. рис. 7, 8). Модель первого порядка точности не дает отрыва ПС, а моделирует только его искажение. Рис. 7. Распределение скорости по толщине пограничного слоя на верхней поверхности профиля, вариант 10, х/с=0,319 V/Vp Рис. 8. Распределение скорости по толщине пограничного слоя на верхней поверхности профиля, вариант 10, х/с=0,90 От надежности моделирования напряжений трения на стенке зависит правильность определения точки отрыва пограничного слоя; ошибочное определение ведёт к искажению коэффициента давления и приводит к ошибкам в интегральных характеристиках. Но, как показывает практика, не всегда нужно уделять большое внимание точности определения напряжений трения. При безотрывном обтекании влияние его мало, а, следовательно, выбор модели, с которой необходимо решать поставленную задачу, существенно облегчается. Поэтому, при расчётах безотрывного обтекания, предварительном анализе схемы течения или в многопараметрических задачах в качестве наиболее экономичной и простой может быть выбрана модель, не учитывающая естественной вязкости. В силу наличия численной диффузии как её дискретного аналога в вычислительной схеме, такая модель часто даёт удовлетворительные результаты, и в совокупности с численными схемами первого порядка точности позволяет значительно экономить требуемые вычислительные ресурсы.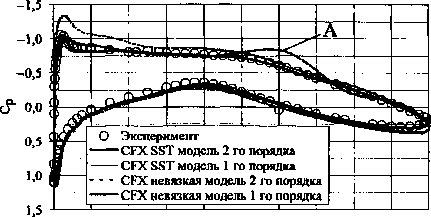
Список литературы Численный анализ влияния поверхностного трения на аэродинамические характеристики профиля
- Белоцерковский О.М. Метод крупных частиц в газовой динамике/О.М. Белоцерковский, Ю.М. Давыдов. -М: Наука, 1982. -704 с.
- Флетчер К. Вычислительные методы в динамике жидкостей: В 2-х т.: пер. с англ./К. Флетчер. -М: Мир, 1991. -Т.1. -504 с.
- Флетчер К. Вычислительные методы в динамике жидкостей: В 2-х т.: пер. с англ./К. Флетчер. -М: Мир, 1991. -Т.2. -552 с.
- Cook Р.Н Aerofoil RAE 2822 -Pressure Distributions, and Boundary Layer and Wake Measurements. Experimental Data Base for Computer Program Assessment/P.H. Cook, M.A. McDonald, M.C.P. Firmin//AGARD Report AR 138. -1979.
- Холст Т.Л. Подведение итогов деятельности рабочей группы по расчёту вязкого трансзвукового обтекания профиля/Т.Л. Холст//Аэрокосмическая техника. -1989. -№11.
- Menter F.R. Two-equation eddy viscosity turbulence models for engineering applications/F.R. Menter//AIAA J. -1994. -№ 1. -P. 1299-1310.
- Белов И.А. Моделирование турбулентных течений: учебное пособие/И.А. Белов, С.А. Исаев. -СПб.: Балт. гос. техн. ун-т, 2001. -108 с.


