Численный метод определения несущей способности плоских вращающихся армированных дисков

Диски компрессоров высокого давления и газотурбинных двигателей работают в условиях высокоинтенсивного нагружения [1] , поэтому актуальными являются проблемы их расчета на прочность и определения несущей способности. Основная масса публикаций по этой тематике содержит результаты математического моделирования механического поведения дисков из однородных конструкционных материалов [1 –4] ; работы же, посвященные дискам из композитных материалов (КМ), малочисленны [5 –9] . При этом в основном рассматривается линейноупругое поведение таких тонкостенных элементов конструкций [1, 5 –8] . Однако расчеты по линейно-упругой модели позволяют установить несущую способность вращающихся дисков только по первому (упругому) предельному состоянию. При создании же изделий разового назначения целесообразно несущую способность дисков оценивать по второму предельному состоянию, в котором материал (или все фазы композиции) становятся пластичнымии. Так, в [9] показано, что даже для дисков из однородных конструкционных материалов предельная расчетная угловая скорость их вращения, определенная по второму предельному состоянию, примерно на 30% больше, чем рассчитанная по первому предельному состоянию. Для армированных дисков различие будет существенно больше, так как при чисто упругом деформировании волокнистых композиций напряжения в армирующих элементах, как правило, не превышают 20% предела текучести [10 –12] , то есть арматура проявляет себя малоэффективно.

Для отыскания несущей способности дисков по второму предельному состоянию можно использовать модель жесткопластического тела [2, 9, 13 –15] . Однако получить полное решение соответствующей краевой задачи удается в редких случаях [9, 14] , особенно для элементов конструкций с неоднородным армированием. Например, в работе [9] утверждается, что для построения полного решения задачи о несущей способности вращающегося КМ-диска прежде всего требуется решить существенно нелинейное функциональное уравнение относительно квадрата его предельной угловой скорости. Известно, что при численном решении подобных уравнений необходимо из каких-либо соображений выбрать «удачное» начальное приближение, достаточно близкое к его корню [16] . Вопрос выбора такого приближения в [9] остался открытым. Поэтому проблема разработки численного метода расчета предельного состояния армированного диска в рамках модели жесткопластического деформирования становится актуальной. Даже если решение и не будет полным, при необходимости оно может

Статья опубликована в открытом доступе по лицензии CC BY 4.0

служить начальным приближением при построении искомого полного решения по алгоритму, описанному в [9] . В [14] для однородных элементов тонкостенных конструкций предложен численный метод, использующий теорию линейного программирования [17] . Этот метод эффективно применен, например, для расчета несущей способности сложно армированных оболочек вращения [18] .

На основании вышеизложенного настоящая работа посвящена разработке численного метода определения верхней (кинематической) границы предельной скорости вращения плоских жесткопластических дисков с осесимметричными структурами армирования, а также изучению зависимостей этой скорости от параметров армирования.

• 2.    Формулировка задачи и метод решения

Как и в [9] , рассматривается плоский тонкий диск, возможной переменной толщины H(r), где r — полярный радиус. Полотно диска ограничено цилиндрическими поверхностями радиусов R 0 и R 1 , при этом R 0 < R 1 (Рис. 1). На внутренней кромке (r = R 0 ) полотно жестко соединено с недеформируемой ступицей (или валом). К внешней кромке (r = R 1 ) могут быть приложены внешние силы от центробежного воздействия разрезной замковой части диска и прикрепленных к ней лопаток [1, 19] .

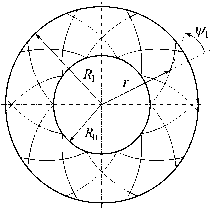
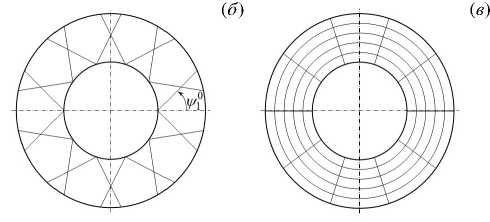
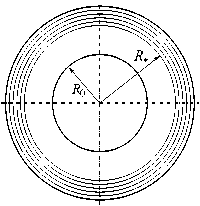
Рис. 1. Структуры армирования диска: по логарифмическим спиралям ( а ); по прямолинейным траекториям ( б ); радиально-окружное армирование всего полотна диска ( в ); окружное армирование внешней подобласти полотна диска ( г )

Полотно диска усилено двумя семействами волокон по осесимметричным траекториям с заданными плотностями p k и углами армирования ^ k (k = 1,2), которые отсчитываются от радиального направления r (см. Рис. 1а , где изображен угол армирования ψ ₁ ). Рассматриваются два варианта укладки волокон:

• 1)    спиральное армирование двумя семействами волокон из одного материала, уложенными симметрично относительно радиального направления r: p 1 (r) = p ₂ (r) и ^ 1 (r) = -^ 2 (r), R 0 <  r <  R 1 (см. Рис. 1 а , б );

• 2)    армирование в радиальном (p 1 (r), ^ i (r) = 0) и окружном (p ₂ (r), ^ 2 (r) = п/2) направлениях (см. Рис. 1 в , г ), при этом различно ориентированные волокна могут быть изготовленными из разных материалов.

Традиционно предполагается, что непрерывные волокна имеют постоянные поперечные сечения [11, 12] , поэтому при укладке первого вида плотность армирования волокнами k-го семейства (k = 1 и/или k = 2), осесимметрично уложенными по спиральным траекториям, вычисляется по формуле [9] :

P k (r) = H o R o ^ k cos^ ° /[H(r)rcos^ k (r)], R o <  r <  R i , H o = H (R o ), pl = p k (R o ), ^ 0 = ^ k (R o ), ^ = n/2,

где p k >  0 — заданная на внутренней кромке плотность армирования. При радиальном армировании в (1) следует принять ^ k = ^ _k = 0. В случае второй структуры плотность армирования окружного семейства р ₂ (r) может быть задана произвольной неотрицательной функцией r. При любых структурах армирования функции p _k (r) должны удовлетворять физическому ограничению [9] :

P s (r) = Xp k (r) <  P m =const < 1 (p k (r) >  0, k =1, 2), R o <  r <  R i ,               (2)

k =1

где p m >  0 — предельно допустимое максимальное значение суммарной плотности армирования р ^ (r) (на практике обычно принимают p m = 0.7 [20] ).

У материала связующей матрицы возможна цилиндрическая анизотропия; а все фазы композиции могут иметь разные пределы текучести на растяжение и сжатие.

Как и в [9] , рассматривается лишь случай осесимметричного деформирования полотна плоского диска в режиме установившегося вращения под действием центробежных сил, так как традиционно это базовый этап его расчета на прочность [1, 19] . Воздействие набегающего воздушного потока, вызывающего изгиб диска и лопаток, пока не учитывается, потому что для этого требуется предварительное построение поверхностей текучести для полотна КМ-диска в четырехмерном пространстве изгибающих моментов и растягивающих мембранных усилий. Однако эта самостоятельная и весьма сложная проблема структурной механики композитов остается за рамками настоящей работы. Данные обстоятельства целесообразно принимать во внимание в последующем при моделировании предельного состояния искривленных КМ-дисков [1] , в которых изгиб неизбежно возникает уже за счет доминирующих в них центробежных сил вращения, а не только от действия набегающего воздушного потока.

Таким образом, результаты предлагаемого исследования, строго говоря, соответствуют моделированию плоского диска в условиях разгонных испытаний на экспериментальном стенде, что также имеет практическое значение. На основании этого по-прежнему используются традиционные гипотезы [1, 9, 19] , согласно которым в диске реализуется обобщенное плоское напряженное состояние (ПНС). При указанных структурах армирования, свойствах связующей матрицы, геометрии, типах закреплении и видах нагружения вращающегося диска направления главных напряжений, деформаций и их скоростей совпадают с радиальным, окружным и поперечным направлениями. Решение зависит только от радиальной координаты r.

При сделанных предположениях на элемент композиции полотна диска, который вращается с постоянной угловой скоростью ω, в радиальном направлении действует центробежная массовая нагрузка [1, 9, 19] :

f (r) = f (r)^2, f (r) = P(r)r, Ro < r < R1, где

P(r)= Po(r)Po + ^Pk (r)Pk, Mo(r) = l- J^Mr);

k=1

ρ 0 , ρ k — объемная плотность материала связующего и волокон k -го семейства, ρ — объемная плотность композиции, µ 0 — относительное объемное содержание связующей матрицы в репрезентативной ячейке композиции.

В предельном состоянии диска — состоянии пластического течения — имеют место кинематические соотношения [9] :

С 1 (г)= dv(r)/dr, ^ 2 (r) = v(r)/r, R o <  r <  R i ,                             (5)

где v — радиальная скорость перемещения точек полотна диска, ξ 1 , ξ 2 — скорости его деформаций в радиальном и окружном направлениях соответственно.

Кроме равенств (5) , должны выполняться:

– уравнение равновесия элемента полотна диска (см. (3) в [9] )

(rH (r)a _i (r)) - H(r)& ₂ (r) = -rH(r) f (r)^ ² , R _o 1 ;

dr

– условие текучести композиции (см. (5) в [9] )

f (a i ,ff 2 ;r)=0, R o <  r <  R i ;

– соотношения ассоциированного закона течения для композиции (см. (9) в [9] )

∂

&(r)= A(r) — f (^ i ,a 2 ;r), R o <  r <  R i (i = 1,2).

Здесь и далее: σ 1 , σ 2 — радиальное и окружное усредненные напряжения, которые совпадают с главными напряжениями в композиции полотна диска (в случае однородного материала диска это обычные напряжения); f — известная функция текучести, явно зависящая от r , так как в общем случае структура армирования неоднородна по радиальной координате (см. Рис. 1 и выражения (1)); λ — неопределенный множитель Лагранжа в жесткопластической модели, причем в точках подобласти пластического течения полотна диска А > 0, а в абсолютно жестких подобластях, где пластическое течение отсутствует, А = 0. В случае КМ-диска под a _i и σ 2 понимаются напряжения, традиционно усредненные по представительному элементу композиции с учетом напряженного состояния в ее компонентах и структуры армирования в этом элементе [20] (подробнее см. в следующем 3-м разделе).

На внутренней кромке диска, в силу его жесткого закрепления на недеформируемом валу (или ступице) имеет

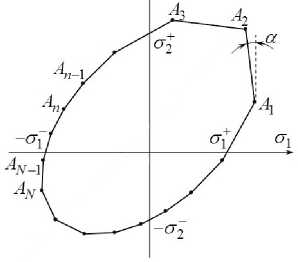
( a )

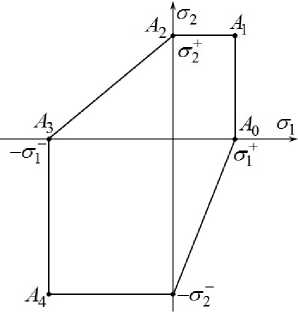
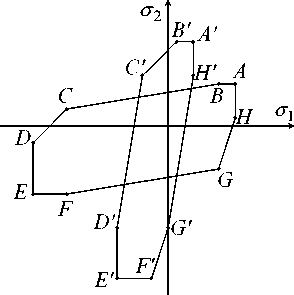
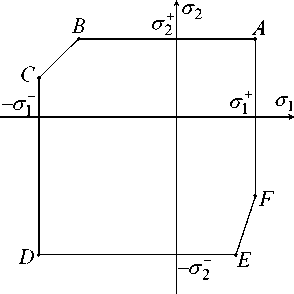
Рис. 2. Кусочно-линейные кривые текучести материала диска: общий случай ( а ); модифицированный критерий Треска–Ху для ортотропного материала ( б ); при армировании по спиральным траекториям ( в ); при радиальноокружной укладке волокон ( г )

место кинематическое граничное условие:

v(R o )=0. (6)

К внешней кромке r = R 1 может быть приложена погонная сила T 1 , действующая в радиальном направлении и порожденная лопатками и разрезной замковой частью диска. Согласно Замечанию 1 из [9] , эта сила выражается так (см. формулу (11) в [9] ):

^T 1 = T 1 ^ 2 , Т 1 = 2 H * ⁽ Р о Р о + Р * Р * ⁾ ( ^R 2 ^— R 2 ) , Р * = 1 ^— Р * , R 2 = ^R 1 + l. ⁽⁷⁾

Здесь принято, что в первом приближении лопатки представляют собой прямолинейные стержни длиной l и толщиной H ∗ в осевом (перпендикулярном плоскости рисунка 1) направлении, усиленные продольно одним семейством волокон с плотностью армирования р * = const >  0. В соотношениях (7) р 0 , р * — объемные плотности связующего и волокон лопатки.

Как видно из выражений (3) и (7) , внешние нагрузки, действующие на диск, пропорциональны квадрату угловой скорости его вращения, поэтому величину ω ² можно трактовать как параметр нагружения рассматриваемой конструкции.

Предполагается, что кривая текучести композиции в главных усредненных напряжениях σ 1 и σ 2 аппроксимирована кусочно-линейно (Рис. 2, где σ ₁ ^± и σ ₂ ^± — пределы текучести материала при растяжении (+) и сжатии (–) в радиальном и окружном направлениях соответственно).

Внешние силы f и T ₁ ¹ , действующие на диск, пропорциональны параметру нагружения ω ² (см. (3) и (7) ), причем для коэффициентов f (r) и T 1 при определении верхней (кинематической) границы предельного значения ω ² выполняется условие нормирования [14] :

R 1

2nR_rT 11 v

(R 1 ) + 2п У

H (r)f (r)v(r)rdr = 1,

R 0

где учтено граничное условие (6) .

Для получения предельного значения угловой скорости вращения диска используется принцип возможной мощности [14, 15] , из которого следует, что для определения верхней границы несущей способности вращающегося диска необходимо найти минимум ( ω _m ² ) параметра внешней нагрузки ω ² :

R 1

ω

2 m

= min^ ² = min2n v ( r )

У H (r)D(r)rdr

R 0

при условии нормирования (8) и выполнении неравенств

D(r) >  ° i,n € 1 + ° 2,n € 2 ,   n = 1, 2,...,N  (D >  0),                            (10)

где D — мощность диссипации механической энергии, σ1,n и σ2,n — значения главных усредненных напряжений в n-м угле кусочно-линейной кривой текучести композиции диска при ПНС, N — количество угловых точек на этой кривой. Система неравенств (10) при учете (5) характеризует известное свойство диссипативной функции [14, 15], состоящее в том, что мощность «ассоциированных» напряжений σi на соответствующих скоростях 2

деформаций ^ i (D = ^^a i ^ i ) больше или равна мощности любого не «ассоциированного» напряжения a i,n на i =1

скоростях деформаций ξ i .

З а м е ч а н и е 1. В работе [9] показано, что в предельном состоянии вращающегося диска реализуются только напряжения σ 1 и σ 2 в точках на верхней части кривой текучести (см. ломаную A 1 A 2 ...A N - 1 A N на Рис. 2а ). При этом под первым узлом (n = 1) этой части кривой следует понимать крайнюю правую точку (см. A i ), а под последним узлом (n = N ) — крайнюю левую точку (см. A N ). Если кривая текучести имеет вертикальные участки (см. отрезки A 0 A 1 и A 3 A 4 на Рис. 2б ), то первым узлом верхнего участка кривой текучести нужно считать верхнюю точку правого вертикального участка (см. A 1 ), а под N-м узлом — верхнюю точку левого вертикального участка (см. A 3 ; в этом случае N = 3). Таким образом, в неравенствах (10) в качестве N целесообразно брать не количество всех угловых точек на кривой текучести композиции полотна диска, а только число узлов, соответствующих верхней части этой кривой, как изображено на рисунке 2а и 2 б . Это позволяет в последующем существенно уменьшить объем вычислений и объем резервируемой машинной памяти.

Минимизация функционала (9) при ограничениях (6) , (8) и (10) с учетом выражений (5) выполнена методами линейного программирования. Для этого сформулированная экстремальная задача сначала дискретизировалась.

На отрезке r G [R 0 ,R 1 ] вводилась равномерная сетка r m = r 1 + (m - 1) A (r 1 = R 0 , m =1, 2,

..

., M ) с шагом

A =(R1 -R0)/(M — 1), где M — число узлов сетки. В качестве неизвестных сеточных функций использовались vm = v(rm) и Dm = D(rm), 1 < m < M. Интегралы в соотношениях (8) и (9) приближенно вычислялись согласно формуле трапеций. В первом равенстве из (5) производная заменялась скошенным конечно-разностным аналогом на трехточечном шаблоне {rm-1 ,rm,rm+1} [21, 22] и подставлялась в неравенства (10). Такая дискретизация имеет 2-й порядок точности по A. В узлах rm (1 < m < M — 2) производная в (5) аппроксимировалась конечной разностью, скошенной влево, а в узлах rM-1 и rM — скошенной вправо. Применение во внутренних узлах rm (2 < m < M — 1) центральной конечной разности при аппроксимации производной в (5) приводит к неустойчивой численной схеме (см. ниже).

В результате ставшая дискретной экстремальная задача (5) , (6) , (8) – (10) при учете выражений (3) , (4) и (7) решалась симплекс-методом Данцига [17] . Предварительно за счет дискретизаци ограничений–равенств (6) и (8) из рассмотрения исключались два узловых значения радиальной скорости — v 1 и, например, v M . Затем составлялся (2M — 2)-компонентный вектор неизвестных величин:

Согласно геометрической интерпретации, дискретизированные и преобразованные при учете (5) ограничения– неравенства (10) , в том числе и D >  0, в евклидовом (2M — 2)-мерном пространстве x G R образуют некоторый выпуклый многогранник Ω , в одной из вершин которого дискретизированная и преобразованная (после исключения v 1 и v M ) целевая функция (9) достигает минимума. Симплекс-метод реализуется как специальное правило перехода от некоторой данной вершины многогранника Ω к такой соседней его вершине, в которой значение целевой функции принимает наименьшее значение. В силу этого алгоритм симплекс-метода обладает свойствами монотонности и конечности, то есть каждый шаг алгоритма приближает к искомому значению целевой функции, и количество таких шагов конечно.

Симплекс-метод Данцига относительно рассматриваемой задачи воплощен автором в программе на языке Fortran. Все расчеты проводились с двойной точностью.

З а м е ч а н и е 2. На каждом шаге симплекс-метода используются модифицированные жордановы исключения, которые можно трактовать как обобщение метода исключения Гаусса при решении систем линейных алгебраических уравнений (СЛАУ) [17] . Поэтому в случаях очень мелкой дискретизации задачи (слишком малого шага A > 0) при вычислениях симплекс-методом возникает проблема «малых знаменателей», так как дискретный аналог исследуемой задачи становится плохо обусловленным (аналогичная проблема возникает и тогда, когда для решения СЛАУ большой размерности, полученной при слишком мелкой дискретизации области интегрирования при применении МКЭ, прибегают к методу Гаусса). Разработка специальных итерационных процедур для решения сформулированной задачи в случаях плохой обусловленности ее дискретного аналога выходит за рамки настоящей работы.

Достигнутое таким образом численное решение рассматриваемой задачи не является полным, так как не позволяет определить в узловых точках r m искомые напряжения a ₁ (r _m ) и a ₂ (r _m ) (1 <  m <  M ). Для построения решения дискретной задачи, согласно неравенствам (10) , необходимо располагать выражениями для напряжений & i, _n (i = 1,2 и 1 <  n <  N ) при конкретных структурах армирования.

• 3.    Кривые текучести композиций армированных дисков

Чтобы определить значения напряжений < 1 ,n и < ₂ ,n (1 <  n <  N ) в соотношениях (10) , нужно иметь кусочно-линейные кривые текучести композиций армированных дисков, в которых приближенно реализуется ПНС. При этом, как уже отмечалось, напряжения c i в радиальном (i = 1) и окружном (i = 2) направлениях (в связующем материале и в композиции) есть главные напряжения для заданных структур армирования дисков.

По аналогии с [18, 23] кривые текучести композиций рассчитаем по структурной модели многонаправленно армированного слоя, которая учитывает ПНС во всех компонентах композиции [24] . Принимаем, что материал связующей матрицы не только по-разному сопротивляется растяжению и сжатию, но и является ортотропным, причем главные оси анизотропии совпадают с радиальным, окружным и поперечным направлениями в диске.

Обозначим через < m i >  0 пределы текучести связующего материала при растяжении (+) и сжатии (-) в радиальном (i = 1) и окружном (i = 2) направлениях. Предполагаем, что кусочно-линейная кривая текучести связующей матрицы при ПНС соответствует модифицированному критерию Треска [25] (Рис. 2б , где σ _i ^± ≡ σ _m ^± _i , i = 1,2). В случае < m 1 = < m 2 и < _{m 1} = < _{m 2} получаем критерий текучести Ху [26] для изотропного связующего, по-разному сопротивляющегося растяжению и сжатию, а при < +1 = < + ₂ = < _m1 = c ^- 2 — критерий текучести Треска [14, 15] .

1-й вариант армирования. Пусть σ _[ ⁺ _{k ]} и σ _[ ^- _{k ]} — пределы текучести материала волокон k-го семейства при растяжении и сжатии (c ± ] > 0, k = 1,2). При таком — спиральном — виде армирования (см. Рис. 1 а , б ) имеем: ^ ₂ (r) = - ^ 1 (r), М 2 (r) = М 1 (r) и < ± ] = c ± ] (R ₀ <  r <  R 1 ). Согласно результатам работы [23] , кривая текучести композиции диска при указанных параметрах армирования представляет собой восьмиугольник ABCDEFGH (Рис. 2в ) при 0 <^ 1 <п/4 или A ’ B ’ C 'D‘ E ‘ F ‘ G ’ H ‘ при п/4<^ 1 <п/2.В силу сделанного выше Замечания 1 в настоящем исследовании интерес представляют только точки (см. Рис. 2а , б ) A ≡ A 1 , B ≡ A 2 , C ≡ A 3 , D ≡ A 4 или A ’ = A 1 , B ’ = A 2 , C ‘ = A 3 , D ‘ = A 4 . Координаты < 1 ,n и < ₂ ,n (1 <  n <  N = 4) данных угловых точек вычисляются так [18, 23] :

A 1 : < 1 = < 1 , 1 = ст+ +< 7 +1 , < 2 = < 2 , 1 = < + +<7 +2 ;

A 2 ^:   < 1 = < 1 , 2 = f,  < 2 = < 2 , 2 = CT ⁺ 2 + j +2 ;

A 3 :

( < 1 = < 1 , 3 = - f  < 2 = < 2 , 3 = - f ⁺ < +2   ( f /< - <  < +2 ^/ < _m 1 ⁾ ;

[ < 1 = < 1 , 3 = < ^{+ -} < m 1 ,  < 2 = < 2 , 3 = <+    (Ё^^П >< m, 2 ^/ < _m 1 ⁾ ;

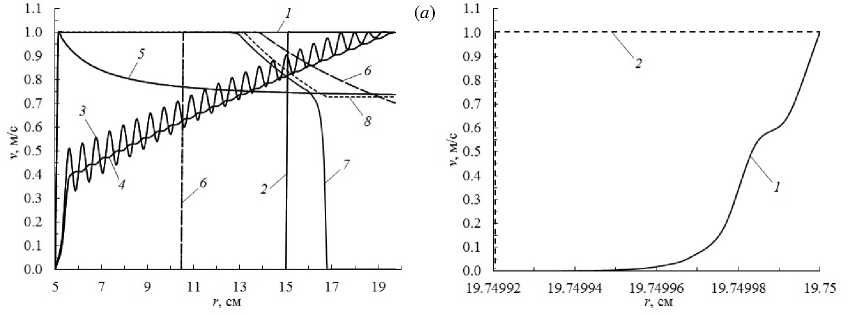
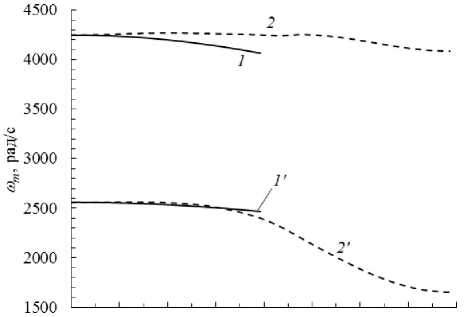
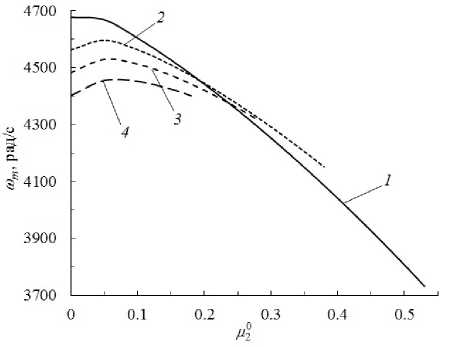
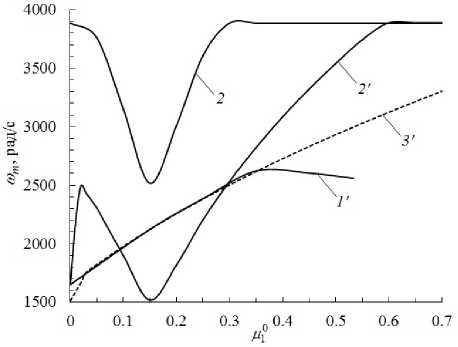
A4 :  <1 = <1,4 = -<-1 -

<±i = ²<±]М1^(r)l2i^(r),<mi = (1^-2М1 ^(r)l2i^(r))<mi ⁽ⁱ=^1,2), l11 =COS^1^(r), l12 s'nQ^(r),    ⁽¹²⁾

а плотность армирования м1 (r) определяется по формуле (1) при k = 1.

2-й вариант армирования. Повторяя рассуждения из раздела 3 в [23], получаем, что при радиально-окружной структуре армирования (см. Рис. 1в, г) кривые текучести композиции диска представляют собой шестиугольник ABCDEF (Рис. 2г). По-прежнему, согласно Замечанию 1, интерес представляют только точки A≡ A₁, B ≡A₂ и C = A₃(N = 3), координаты которых вычисляются по формулам [9, 18, 23]:

A1^:  <1=<1,1=<⁺1+<m1,  <2=<2,1=<+2+<m2;

A2 ^:<1 = <1,2 = -<-1, <2 = <2,2 = <+2 ⁺<m2;                             (13)

A3 :  <1 = <1,3 = -< -1 -

<mi=⁽¹-Mi^(r))<mi, <±i=<±Mi^{(r) (}i=^1,2);                              ⁽¹⁴⁾

интенсивность армирования м1 (r) выражается формулой (1) при ^1 (r) = 0 (k = 1), а м2 (r) может быть задана достаточно произвольно при выполнении физических ограничений (2).

Таким образом, равенства (11) и (13) при учете (1), (2), (12) и (14) конкретизируют значения напряжений 1,n и <₂,_n(1 < n < N) в неравенствах (10) для выбранных структур армирования.

• 4.    Верификация численного метода

С целью верификации разработанного численного метода решения экстремальной задачи (5), (6), (8)–(10)

рассмотрим тестовую задачу, для которой в [9] построено полное решение в аналитическом виде. Предполагаем, что диски являются либо однородными, для материалов полотна которых кривые текучести представлены на рисунке 2б, либо композитными (со 2-м вариантом армирования), их кривые текучести материала композиции изображены на рисунке 2г. В работе [9] показано, что в этих случаях квадрат предельной угловой скорости вращения диска ш²определяется из линейного уравнения:

R1

R1T +

У H (r)p(r)r² dr

R₀

R1

ш²= RoH (R₀)a+(R₀) +

JH (r)a+ (r)dr,

R₀

где в случае однородного диска о⁺= const (i = 1,2)и р = const — известные характеристики материала; в случае же КМ-диска p(r) находится по формуле (4), а напряжения о+ (r) и о+ (r) рассчитываются так (см. Рис. 2г и соотношения (13) при учете (1) и (14)):

°^+(r)= ^о1,1 = fl + ^1, °+^(r)= ^о2,1 = f ⁺ ^ ⁽¹⁶⁾

Если заданы толщина полотна диска H(r), его структура армирования (функции ^1 (r) и ^₂(r)) и сила T1 (см. (7)), то при учете (4) и (16) правая часть в (15) и выражение, заключенное в квадратные скобки, известны, поэтому из (15) однозначно вычисляется величина ш².

В [9] установлено, что при некоторых схемах армирования диска в окрестности его внутреннего контура r = R_o в предельном состоянии может возникнуть жесткая подобласть R_o< r< r^ (r* ₁),b точках которой напряжения не достигают пластического состояния: фазовые точки (^1,^₂) не находятся строго на кривой текучести, а располагаются с ее внутренней стороны. Поэтому в указанной подобласти, согласно ассоциированному закону течения, имеем £1 (r) = (₂(r) = 0, а из соотношений (5) вытекает, что v (r) = 0 (R_o< r< г₊),то есть эта часть диска не деформируется (не «течет»). Аналогичная жесткая область может возникнуть и в однородном диске при H(r) = const, если в окрестности внутренней кромки r = R_o толщина полотна избыточна. Поэтому, строго говоря, в формуле (15) необходимо R_oзаменить на r^ и затем минимизировать величину ш²при варьировании r^ G [Ro,R1).

Далее рассмотрим конструкцию, состоящую из диска, ограниченного кромками радиусов R_o = 5 см и R1 = 19.75 см, и лопаток длиной l = 11.4 см [19] и толщиной H =0.5 см (см. (7)). Диск однородный, выполнен из магниевого сплава МА2 (0^1 = ^m2 = 151 МПа, a_m1 = a_m2 = 113 МПа и р₀= 1740 кг/м³[12, 27]) или из стали 35ХГСНА (^ = ^2 = 1554 МПа, о- 1 = о-₂ = 1754 МПа и ро = 7800 кг/м³[12, 27]), а также армирован и состоит из магниевой матрицы (сплав МА2) и двух (в частности одного) семейств углеродных волокон Торнел-400 (о+] = о- = 2750 МПа и р_к = 1780 кг/м³, k = 1,2 [12]). Лопатки изготовлены из сплава МА2 и усилены в продольном направлении волокнами Торнел-400 с плотностью армирования ^* =0.6 (см. (7)). Согласно Замечанию 1 в [9], для учета влияния замковой части обода диска в (7) объемную плотность материала связующего лопатки искусственно увеличим до значения рЦ = 2700 кг/м³, то есть возьмем не р0 = 1740 кг/м³, как приведено выше для магниевого сплава МА2.

Диски имеют постоянную толщину (H(r) = H = const), толщину полотна изотропного диска из сплава МА2 примем равной H = 0.8 см. Массу этого диска считаем эталонной:

me = 1.596 кг.

Толщину других дисков, в частности композитных, подбираем так, чтобы их масса m равнялась эталонной (17). Так, например, для диска из стали марки 35ХГСНА получаем H = 0.1785 см. Толщина КМ-дисков, обладающих всюду суммарной плотностью армирования ^^ = 0.7 (см. (2)), составляет H = 0.7873 см как при однородном окружном (^1 = 0, ^₂= 0.7), так и при неоднородном радиально-окружном (^1 = 0.7 и ^₂(r) = ^° — ^1 (r)) армировании; в последнем случае выражение для ^1 (r) дано в (1) при k =1.

Такой же толщиной обладает и рассматриваемый далее КМ-диск с однородной радиально-окружной структурой при ^1 (r) = ^₂(r) = 0.35, у которого тоже ^^ = 0.7. В таблице 1 приведены значения предельной угловой скорости вращения ωm , рассчитанные по формуле (15) и найденные численно по формулам (5), (6), (8)-(10) с учетом (3), (4), (7), (13), (14) и (16), при разной степени дискретизации отрезка r G [R₀,R1 ] (при различном числе M узлов сетки). Расчеты проведены для двух вариантов конструктивного исполнения: при отсутствии лопаток (см. (8) и (15) при T1 = 0) и при наличии лопаток (см. (8) и (15) при учете (7)). В таблице 1 указаны значения r∗ , определяющие левую границу области пластического течения полотна диска в предельном состоянии. Прочерки означают, что при выбранной дискретизации (заданном M) подобласти пластического течения r G [r*,R1] получить численное решение экстремальной задачи не удалось.

Последнее обстоятельство объясняется тем, что для соответствующих КМ-дисков с лопатками r∗ стремится

Таблица 1. Расчетные значения предельной угловой скорости вращения дисков ωm, [рад/с]

Материал диска Наличие лопаток r∗ Аналитическое решение Численное решение M = 13 M = 26 M = 51 M = 101 M = 201 Магниевый сплав МА2 – R0 2604.7 2484.5 2503.3 2512.6 2516.8 2518.9 + R0 1570.7 1496.0 1508.2 1514.5 1517.3 1518.8 Сталь марки 35ХГСНА – R0 3946.6 3764.4 3794.0 3807.0 3813.4 3816.6 + R0 2379.9 2266.7 2286.0 2294.7 2299.0 2301.2 КМ-диск: М1 = 0 и М2 = 0.7 – 0.76R1 6750.2 6568.2 6576.3 6579.8 6581.6 6582.5 + ≈R1 1953.3 1641.1 – – – – КМ-диск: м1 =0.7 и М2(г) = М1 -М1(г) – R0 7690.7 7319.6 7324.6 7324.7 7324.9 7325.1 + ≈R1 3931.0 3302.7 – – – – КМ-диск: М1(г)= М2 (r) = 0.35 – R0 6848.4 6532.2 6583.6 6606.2 6617.3 6622.7 + R0 4129.7 3933.2 3966.8 3981.9 3989.4 3993.2 к R1. Очевидно, что в таких предельных случаях численное решение недостижимо, так как и Д ^ 0, поэтому в таблице 1 приведены значения wm, рассчитанные при г* = (1-10-7) R1 и R1. Однако при столь близком к R1 задании r∗ пластическое течение в КМ-дисках развивается в очень узкой подобласти: r∗ < r ⩽ R1 , и уже при выборе M = 26 шаг дискретизации задачи составляет Д = 7.9 • 10-10 м. Согласно же формулам (13) и (14), в дискретизированных с учетом (5) ограничениях–неравенствах (10) при таком шаге ∆ коэффициенты при vm имеют порядок1018^1019 Па/м, что можно уже трактовать как машинную бесконечность, по сравнению с единицей (коэффициентом при Dm в (10)), даже при использовании двойной точности расчета. Поэтому в силу Замечания 2 в рассматриваемых случаях для КМ-дисков дискретная задача при M ⩾ 21 становится плохо обусловленной и разрешить ее симплекс-методом не удается.

Следует подчеркнуть, что не для всех КМ-дисков с лопатками возникает ситуация, когда r* ^ R1. Так, при спиральном армировании (см. далее подраздел 5.1.) при многих углах укладки волокон получается r∗ = R0 или r∗ > R0, но существенно отличное от R1 (R0 < r∗ < R1).Тогда численное решение можно построить при разных числах M, вплоть до M = 201. В этом смысле КМ-диски, напротив которых в таблице 1 стоят прочерки, оказались исключениями с «неудачно» выбранными структурами армирования, но в то же время для них реализуемо аналитическое решение (см. (15) при учете (16)). В связи с этим обстоятельством в конце таблицы 1 приведены данные дополнительного расчета для диска с однородной радиально-окружной структурой при м1 = м2 = 0.35. При этом как с лопатками, так и без них численное решение не только возможно, но и обладает хорошей сходимостью. Так, при M = 201 оно отличается от аналитического всего на 3.3%. В предельном состоянии пластическое течение охватывает все полотно диска. Однако следует подчеркнуть, что однородная радиально-окружная структура в определенном смысле является идеализированной, так как в этом случае µ1 (r) = µ⁰₁= const, то есть для радиального семейства волокон не выполняется равенство (1) при k = 1 и ψ1 (r) =ψ₁⁰=0, H(r) = const. Реализовать такую структуру на практике можно либо за счет использования волокон радиального семейства, имеющих по радиусу r специально подобранную переменную толщину, либо за счет укладки волокон радиального семейства постоянного поперечного сечения, но обрывающихся внутри области армирования. Такие меры позволяют обеспечить равенство µ1 (r) = const. Далее однородные радиально-окружные структуры армирования полотна диска рассматриваться не будут.

На рисунке 3 изображены нормированные зависимости v(r), рассчитанные численно для некоторых случаев предельных состояний однородных изотропных и КМ-дисков. Кривая 1 на рисунке 3а соответствует тем случаям, для которых в таблице 1 указано значение r_∗ = R₀, и она полностью согласуется с аналитическим решением, полученным в [9]: v(r) = v0 = const > 0 при R0 < r ⩽ R1, а в точке r = R0 функция v(r) испытывает скачок от нуля (в силу граничного условия (6)) до значения v0 (на Рис. 3а принято v0 = 1 м/с):

v(r) =

0, r=R0, v0 = const > 0,

R0⩽R1.

Кривая 2 на рисунке 3а отвечает предельному состоянию вращающегося диска с однородным окружным армированием (^1 = 0 и м2 = 0.7) при отсутствии лопаток. При этом в предельном состоянии в окрестности внутреннего контура диска образуется жесткая подобласть: R₀⩽ r ⩽ r_∗ = 0.76R₁(см. Табл. 1). Кривая 2 также согласуется с аналитическим решением (18) при замене R0 на r∗. Поэтому в тех случаях, для которых в таблице 1 радиус r*= R1, наблюдается хорошее совпадение численно найденных значений wm с рассчитанными аналитически по формуле (15) при учете (16). Численные значения ω_m, отличаются от точных значений ω_m(см. (15)) всего на2.5^4.8%. В этих случаях, каквидноиз таблицы 1, wm, полученные численно при разных значениях M,

(б)

Рис. 3. Скорость радиального смещения точек диска в предельном состоянии: протяженная область пластического течения (а); пластическое течение локализовано в малой окрестности внешнего контура (б) (см. пояснения в тексте)

с увеличением M стремятся к некоторым предельным числам, и для проведения практически приемлемых расчетов вполне обоснованно можно принимать M = 51, так как при М> 51 значения wm уточняются незначительно.

Напомним, что приведенные в таблице 1 значения ωm, рассчитанные численно, установлены при аппроксимации производной в (5) ее дискретными аналогами на трехточечном шаблоне с использованием скошенных конечных разностей. Если для внутренних узлов сетки rj (2 < j< M — 1) применить центральные конечные разности [21,22], то расчетные зависимости v (r) будут существенно отличными от кривой 1 на рисунке 3а. Так, кривые 3 и 4 (Рис. 3а) определены на основе центральных конечных разностей при расчете предельного состояния вращающегося магниевого диска из сплава МА2 без лопаток (кривая 3) и при их наличии (кривая 4). Видно, что кривые 3 и 4 не только количественно, но и качественно отличаются от кривой 1 и совершенно не согласуются с точной зависимостью v(r) (см. (18)). Поэтому значения ωm, вычисленные при помощи центральных разностей, сильно отличаются от точных значений, рассчитанных по формулам (15) и (16). Так, при M = 51 для магниевого диска без лопаток расчетное значение равно: wm = 1996 рад/с, а для такого же диска с лопатками — wm = 1125 рад/с. Эти величины отличаются от точных (см. Табл. 1) на 23.4% и 28.4% соответственно. Поэтому нецелесообразно применять центральные конечные разности во внутренних узлах rj сетки для аппроксимации производной в первой формуле (5).

При аппроксимации же производной в (5) на основе двухточечного шаблона {rj ,rj+1} (то есть с меньшей на порядок точностью по Д[21, 22]) для случаев, приведенных в таблице 1 при r* = R1, расчетные зависимости v (r) получаются совпадающими с кривыми 1 и 2 на рисунке 3а. Однако при этом предельные численные значения ωm хуже согласуются с точными значениями ωm, чем численные результаты, приведенные в таблице 1. Так, при M = 51 и использовании аппроксимации производной в (5) на двухточечном шаблоне для магниевого диска без лопаток имеем wm = 2426 рад/с, а с лопатками — wm = 1462 рад/с. Оба эти значения отличаются от точных на 6.9%, в то время как аналогичные значения из таблицы 1 (см. две первые строки при M = 51) отличаются от точных всего на 3.5%. Поэтому в настоящем исследовании для аппроксимации производной в (5) далее применяются скошенные конечные разности именно на трехточечном шаблоне.

Как видно из таблицы 1, только для дисков с окружной и неоднородной радиально-окружной структурами армирования при наличии лопаток численные значения wm, полученные при M =13 (при остальных M в таблице стоят прочерки) существенно отличаются от аналитических значений, рассчитанных по формулам (15) и (16). Объясняется это, по-видимому, тем, что, согласно численному решению в предельном состоянии, полотно диска в этих случаях течет в очень малой окрестности внешней кромки (r* ^ R1). При этом зависимость v(r), построенная по данным, найденным численно (см. кривую 1 на Рис. 3б) существенно отличается от аналитической кривой 2 из [9] (см. (18) при замене R₀на r_∗и ^r* ^ R₁). В частности, кривая 1 рисунка 3б на левом участке гладко сопрягается с горизонтальной осью r, то есть на границе раздела пластического течения (r > r∗ ) и абсолютно жесткой области в диске (R0< r< r*) радиальная скорость течения v(r) изменяется без скачка и излома, как это наблюдается на кривой 2. Кинематически допустимое поле скоростей, соответствующее кривой 1 на рисунке 3б, приводит к существенно меньшему (на 16%) предельному значению ωm, чем в аналитическом решении.

В работе [9] показано, что, согласно аналитическому решению, в предельном состоянии диска на границе между абсолютно жесткой и пластической подобластями при r = r* + 0 имеет место режим пластического течения в точках A1 или A (или А’) на кривых текучести (см. Рис. 2). Так как в рассматриваемых случаях r* ^ R1, то на внешней кромке полотна диска никакой другой режим течения не может реализоваться, поэтому при r* ^ R1 значение ωm сразу же рассчитывается по формуле (15) с учетом (16) при замене R0 на r∗ и предельном переходе r* ^ R1. Таким образом, если численное решение указывает на то, что в предельном состоянии диска r* ^ R1, то этот результат можно трактовать как подсказку к возможности обоснованно использовать аналитическое решение (15), (16) при r∗ → R1 . Причем данный результат справедлив для любых структур армирования, а не только в случаях радиально-окружной укладки арматуры.

Следуя общей логике настоящего исследования, далее в тех случаях, когда r∗ → R1 , будем отдавать предпочтение численному решению, имея в виду, что полученные таким образом заниженные значения ωm , определяют несущую способность вращающихся дисков с запасом.

В работе [28] приведено упругопластическое решение для сплошного (R0 = 0) однородного (р = р₀= const) изотропного вращающегося диска постоянной толщины (H (r) = H = const) без лопаток: T1 = 0 (см. (7)). При этом рассматривалась идеальная пластичность (модель Прандтля) с критерием текучести Треска: о+ (r) = о+ (r) = ^mi = ^т+з = o_m1= o_m2= const (см. (14) и (16) при pi = 0, i = 1,2). В рамках этих предположений установлено, что предельная угловая скорость вращения такого диска, когда пластическое течение охватывает все его полотно, в используемых здесь обозначениях определяется так (см. (10.36) в [28]):

и² = 3^+1/(ро R²).

Нетрудно видеть, что выражение (19) непосредственно вытекает из равенства (15), если в нем учесть сделанные в [28] предположения: R0 = 0, р(г) = р₀ =const, H(r) = H = const, T1 = 0 и o+ (r) = 0^+1 =const.

В таблице 2 приведены значения предельной угловой скорости вращения диска ω_m, полученные по формуле (19) и численно при разных значениях внутреннего радиуса диска R0, стремящегося к нулю. При численном решении принималось M = 51. Значения ш_т, представленные в третьем столбце этой таблицы полностью совпадают с аналогичными значениями в 7-м столбце таблицы 1 (при M = 51).

Таблица 2. Расчетные значения предельной угловой скорости вращения однородных изотропных дисков ωm , [рад/с]

Материал диска	Аналитическое решение (19)	Численное решение (M = 51); внутренний радиус R0, [см]
		5.0	4.0	3.0	2.0	1.0	0.5	0.1	10-7
Сплав МА2	2583.5	2512.6	2518.2	2527.8	2540.3	2554.8	2562.5	2568.7	2570.3
Сталь 35ХГСНА	3914.6	3807.0	3815.6	3830.1	3849.0	3870.9	3882.6	3892.1	3894.4

Как видно из таблицы 2, установленные численно значения ш_т при R0 ^ 0 стремятся к некоторым предельным величинам, которые при R0 = 10^-7см отличаются от аналитического решения (19) всего на 0.51% (при R0 < 10-⁷см уточнение численно определенных значений w_m не наблюдается, по крайней мере в пределах первых 7-ми значащих цифр.)

Таким образом, данные, представленные в таблицах 1 и 2, дают основание доверительно относиться к результатам, получаемым численно по формулам разделов 2 и 3.

• 5.    Анализ влияния параметров армирования дисков на их предельную скорость вращения

• 5.1.    Влияние углового армирования при фиксированном расходе армирующих волокон

Рассмотрим влияние параметров армирования (углов и плотностей) на предельное значение скорости вращения КМ-дисков. Размеры дисков в радиальном направлении и их материалы, а также размеры, структура армирования и материалы лопаток такие же, как в разделе 4.

Вначале обратимся к вырожденному случаю спирального армирования — укладке волокон по прямолинейным (геодезическим) траекториям (см. Рис. 1б), так как такой вид армирования наиболее просто реализуется технологически. В осесимметричном случае углы армирования ^k (r) определяются по формуле Клеро [29]:

rsin^k (r) = R₀sin^° =const > 0, k = 1, 2, R0< r< R1,                      (20)

где ^° — угол армирования волокнами k-го семейства на внутреннем контуре диска r = R0 (см. Рис. 1 б). Согласно (1), при учете (20) плотность армирования p_k (r) при такой укладке волокон монотонно убывает по r, оставаясь положительной при задании pk > 0 (k = 1,2). В случае pi = p0 и ^° = v2 из соотношений (1) и (20) получаем: p₁(r)= p₂(r) и ^1(r) = — ^₂(г). Так как плотности армирования p_k(r) являются убывающими положительными функциями, то выполнение физических ограничений (2) достаточно проверять только на внутреннем контуре диска (r = R0).

Объем диска (Vd) и общий объем волокон в диске (Vf) находятся по формулам:

R1

R1

Vd = 2п ^H(r)rdr, Vf = V1+V2, Vk = 2п fH(r)^k(r)rdr (k = 1, 2).

R0

R0

Как и в разделе 4, рассматриваем диски постоянной толщины H(r) = H = const. Для КМ-диска со структурой армирования(1)и(20)приуглах ■ф⁰ = —■ф⁰ = п/4—ортогональноеармированиевокрестностивнутреннего контура r = R0 (именно этот случай изображен на рисунке 1 б)—примем Мх = м2 = 0.35. При этом выполняется физическое ограничение (2) во всех точках диска с предельным значением Mm = 0.7. Относительный объем арматуры в таком диске составляет: П = Vf/Vd = 0.2155 (см. (21) при учете (1) и (20)). Это значение далее примем за эталонное:

П_е = 0.2155.

Будем варьировать углы армирования ф0 = —ф0 в КМ-диске в пределах ф0 G [0,п/4], а плотности армирования м1 = м2 при разных ф0 зададим такими, чтобы относительный объем арматуры П, определенный с учетом соотношений (1), (20) и (21), равнялся эталонному значению (22). Кроме того, толщину КМ-дисков возьмем такой, чтобы их масса m = Po(Vd — Vf )+piVi + P2V2 (23)

также имела эталонное значение (17). А далее сравним несущую способность КМ-дисков, имеющих одинаковую массу (m = me) при одином относительном расходе арматуры (^ = ^e).

Для дисков с укладкой волокон по геодезическим траекториям (см. (20) и Рис. 1б) углы армирования в диапазоне ф0 G (п/4,п/2) не рассматриваются, так как при этом нарушается физическое ограничение (2) при требовании выполнения условия П = П_е.

В предельном состоянии КМ-диска без лопаток при углах армирования ф0 = — ф20 = п/4 (см. Рис. 1 б) зависимости v(r) отвечает кривая 5 на рисунке 3а (при наличии лопаток зависимость v(r) качественно аналогична кривой 5, поэтому на рисунке 3а она не изображена). Монотонное убывание кривой 5 (за исключением интервала R0 = r 1 С r

0.0    0.2    0.4    0.6    0.8    1.0    1.2    1.4    1.6

^°, рад

Рис. 4. Зависимость предельной угловой скорости вращения диска от угла армирования на его внутреннем контуре: прямолинейное армирование (линии: 1, 1^′); армирование по логарифмическим спиралям (2, 2^′); при отсутствии (1, 2) и с учетом (1^′, 2^′) лопаток

На рисунке 4 изображены значения предельных угловых скоростей вращения диска wm на его внутреннем контуре r = R0 в зависимости от угла армирования ψ10 . На этом и последующих рисунках кривые, номера которых помечены штрихом, рассчитаны при учете наличия лопаток на внешнем контуре, а кривые с теми же номерами, но без штриха, получены при тех же условиях, но в отсутствие лопаток. Сплошные кривые 1 и 1′ на рисунке 4 рассчитаны для рассматриваемого случая армирования дисков по геодезическим траекториям (см. Рис. 1б). Обе кривые монотонно убывают, поэтому из всех прямолинейно армированных дисков наибольшей несущей способностью обладают диски с радиальной укладкой волокон фф0 = — ф0 = 0). Однако при сравнении видно, что кривые 1 и 1′ имеют малую изменяемость (особенно кривая 1′), поэтому варьирование углов ф0 = — ^° незначительно влияет на изменение несущей способности дисков с таким типом структуры армирования.

Рассмотрим другой вид армирования—укладку волокон по логарифмическим спиралям: ф1 (r) = —^2 (r) = ф0,

R0 ⩽ r ⩽ R1 (см. Рис. 1а), тогда для диска постоянной толщины из (1) следует выражение:

Mk(r) = RoMk/r,  k = 1,2, Ro Сr С Ri.

Отсюда видно, что плотности армирования µk не зависят от углов ψ_k⁰и монотонно убывают по r. При задании м1 = м2 из (24) имеем: Mi (r) = М2 (r). Следовательно, укладка арматуры по логарифмическим спиралям с фиксированными значениями м 1 = м2 при любых углах армирования ф⁰€ [0,п/2) приводит к одинаковому общему расходу волокон. Чтобы относительный объем арматуры в таком диске был равен эталонному значению (22), следует задать м0 = М2 = 0.2667. Толщину H КМ-дисков по-прежнему выбираем из условия равенства массы (23) эталонному значению (17), при этом получаем H = 0.7961 см.

На рисунке 3а штриховая кривая 6 характеризует зависимость v(r) в предельном состоянии диска без лопаток, армированного по логарифмическим спиралям при углах ф0 = — ф20 = п/4 — криволинейное ортогональное армирование (именно такая структура изображена на Рис. 1а). Горизонтальному участку кривой 6 на рисунке 3асоответствуют точки диска из интервала 10.7 < r< 13.9 см,в которых на кривой текучести композиции реализуется горизонтальный режим течения AB или A^′B^′(см. Рис. 2в). Правому убывающему участку кривой 6 на рисунке 3аотвечают точки с координатой 13.9 < 19.75 см, в которых на кривой текучести композиции наблюдаются наклонные режимы течения BC, CD или B^′C^′, C^′D^′(см. Рис. 2в). Следовательно, для расчета несущей способности дисков, армированных по логарифмическим спиралям, также нельзя использовать аналитическое решение (15) при учете (16).

Зависимости от угла армирования ψ₁⁰предельной скорости вращения ωm КМ-дисков с укладкой волокон по логарифмическим спиралям изображены на рисунке 4 штриховыми линиями 2 и 2^′. Обе кривые ведут себя немонотонно. Так, на кривой 2 локальный максимум достигается при ф⁰ и п/8,ана кривой 2‘ — при ф ⁰и п/10, то есть наибольшую несущую способность КМ-дискам обеспечивают именно спиральные структуры армирования. Однако изменяемость кривых 2 и 2‘ при ф⁰€ [0,п/6] мала, поэтому указанные локальные максимумы визуально не заметны. Как видно, кривая 2 на рисунке 4 имеет малую изменяемость при всех углах из диапазона армирования ф⁰€ [0,п/2). Кривая же 2 ‘ при ф 0 € [п/4,п/2) заметно убывает, то есть в КМ-диске с лопатками варьирование углов армирования ψ ⁰при укладке по логарифмическим спиралям приводит к существенному изменению допустимой скорости вращения такой конструкции.

В предельном состоянии КМ-дисков с лопатками при углах армирования по логарифмическим спиралям в диапазоне ф⁰€ [0,п/4] зависимости v (r) качественно аналогичны кривым 1 и 2 на рисунке 3а или близки к ним — подобны кривой 5, но с малой изменяемостью, то есть пластическое течение развивается либо во всем полотне дисков (R₀⩽ r ⩽ R ), либо в его внешней кольцевой подобласти конечных размеров (r_∗⩽ r ⩽ R , r* 1). В интервале же ф⁰€ (п/4,п/2) зависимости v(r) имеют вид, аналогичный кривой 1 на рисунке 3б,то есть пластическое течение практически имеет место только в бесконечно узкой зоне в окрестности внешнего контура (r* ч R 1). Именно в диапазоне ф0 € (п/4,п/2) на кривой 2‘ рисунка 4 наблюдается значительное убывание зависимости ωm ψ ⁰(как отмечалось в разделе 4, при r* ч R1 ,то есть в данном случае при ф⁰€ (п/4,п/2), полученные численно значения ординат точек на кривой 2^′можно уточнить за счет аналитического решения (15), (16) путем замены в нем R0 на r∗ и осуществления предельного перехода r∗ → R ).

Кривые 1^′и 2^′на рисунке 4 лежат существенно ниже кривых 1 и 2 соответственно. Следовательно, наличие лопаток приводит к значительному (почти двойному) уменьшению предельной скорости вращения дисков, армированных по прямолинейным и спиральным траекториям.

• 5.2.    Влияние плотностей армирования при фиксированных углах армирования

Исследуем влияние плотностей армирования Mk (r) радиально-окружной структуры (см. Рис. 1 в, г) на значение предельной угловой скорости вращения КМ-дисков при фиксированных углах ф_к(к = 1,2). В осесимметричном случае армирование в радиальном и окружном направлениях совпадает с армированием по направлениям главных напряжений в композиции и скоростей усредненных деформаций. Такие структуры армирования традиционно принято считать рациональными [20].

Первое (к = 1) семейство волокон уложено в радиальном направлении (ф 1 = 0), плотность армирования которого м 1 (r) при H (r) = H = const, согласно (1), вычисляется по формуле (24). Второе (к = 2) семейство волокон уложено в окружном направлении (ф2 = п/2). Его плотность армирования м2 (r) является произвольной функцией r, если при этом выполняются ограничения (2). Для определенности используем линейную зависимость м2(г)= р R0 м2 + R 1 r м2 (м2 = M2(R0), м2 = M2(R 1 ))• (25)

R - R0 R -R0

С целью дальнейшего обоснованного сравнения радиально-окружного армирования со спиральным считаем, что условие одинакового относительного расхода арматуры по-прежнему имеет вид (см. (22)):

Vf V1+V2

^ = f = 1 + ² = ^ = 0.2155.

Vd     Vd

Поскольку у рассматриваемых дисков H(r) = H = const, из (21) при учете (24) (где k = 1) и (25) получаем:

V2 =

Vd = nH(R2-R0),  Vi = 2nHRo(Ri-Ro)мi;

2nH

R₁- R₀

^2—^2 RI - R³⁾+ ^R-^R R — r²⁾

Из равенства (28) следует выражение:

м2=

/ Ri-R3     R2 - R2 \ 1\V2(Ri-Ro)  / R3-R3     R2-R0 \ 0

<       R⁰  2  )  [  2nH  ⁺О   ^R1  ■’  72

в котором, согласно (26) и (27),

V2 = V2 № = nH [^e (Ri - R2) - 2Ro (Ri - Ro>1].

В соотношении (29) при учете (30) и известном значении Ωe (см. (22)) параметры µ⁰₁и µ⁰₂можно варьировать и, в соответствии с (24) и (25), приходить к разным распределениям плотностей армирования. При этом необходимо помнить об ограничениях (2) и м1 ^ 0, м2 ^ 0, м2 ^ 0.

Толщину H дисков с радиально-окружной структурой выбираем такой же, как и в при армировании по логарифмическим спиралям. Это обеспечивает одинаковую массу сравниваемых дисков (см. (17), (23)) и один и тот же общий расход арматуры в них (см. (22) и (26)).

На рисунке 5 изображены зависимости ω_mµ⁰₂, рассчитанные при некоторых значениях µ⁰₁для диска без лопаток с радиально-окружной структурой армирования. Кривая 1 получена при м1 = 0 (окружное армирование), кривая 2 — при м1 = 0.15, кривая 3 — при м1 = 0.25 и кривая 4 — при м1 = 0.35. Кривые 2-4 соответствуют радиально-окружным структурам армирования с разным распределением плотностей армирования м1(г) и M2(r). Правые точки на всех кривых являются предельными, так как при значениях µ₁и µ₂из формулы (29) с учетом (22) и (30) следует: м2 = 0. Дальнейшее увеличение значения м2 при фиксированном м1 приводит к неравенству м2 < 0, что противоречит физическим ограничениям (2).

Поведение кривых на рисунке 5 свидетельствует о том, что в случае радиально-окружной структуры зависимость предельно допустимой скорости вращения ω_mдиска без лопаток от плотностей армирования на внутреннем контуре µ₁иµ₂достаточно сложна. Для диска с лопатками аналогичные кривые 1^′–4^′на рисунке 5 не представлены, так как они лежат значительно ниже кривых 1–4 и визуально совпадают с горизонтальными линиями. Наименьшие значения ординат точек на кривых 1^′–4^′отличаются от наибольших значений менее чем на 1%.

Следовательно, для дисков с лопатками, армированных в радиальном и окружном направлениях, наблюдается практически однопараметрическая зависимость: wm (м1 ,м2) ~ wm (м1). Вычисленная при м2 = 0, она выглядит как кривая 1 ‘ на рисунке 6, которая имеет максимум wm = 2618рад/с в точке м1 ~ 0.35. Точкам левого возрастающего участка кривой 1' в предельном состоянии КМ-дисков соответствует зависимость v (г), изображенная на рисунке 3б, а точкам правого убывающего участка — зависимости v (г), качественно аналогичные кривой 2 на рисунке 3а. Правой точке кривой 1^′рисунка 6 отвечает вырожденный случай — радиальное армирование полотна диска (м1 (r) = 0 и м2 (r) = 0). При м1 > 0.533 относительный объем арматуры в диске ^ будет превышать эталонное значение (22), если дополнительно потребовать м2 (r) = 0 (радиальной укладки волокон), либо получается м2 < 0 при использовании равенств (29), (30) (радиально-окружное армирование) и соблюдении условия (26). Последнее неравенство недопустимо в силу необходимости выполнения физических ограничений (2). Поэтому при 0.533 <м1 С 0.7 = м_т кривая 1 ‘ не приводится.

Из поведения кривых рисунка 5 видно, что для диска без лопаток из всех структур армирования по радиальным и окружным направлениям наибольшую предельную скорость вращения ωm обеспечивает окружная укладка волокон при значении м2 = 0 (см. левую точку на кривой 1). Согласно же формуле (25), значению м2 = 0 соответствует возрастающая по линейному закону плотность армирования м2 (r). Это позволяет сделать предположение, что для увеличения несущей способности вращающегося диска без лопаток при фиксированном расходе арматуры (см. равенство (26)) целесообразно более интенсивно усиливать внешнюю подобласть полотна диска, прилегающую к внешнему контуру r = R1.

В связи с этим далее рассмотрим случай армирования не всего полотна диска (R0 ⩽ r ⩽ R1 ), а только

Рис. 5. Предельная угловая скорость вращения диска без лопаток с радиально-окружной структурой армирования при r = R0 в зависимости от плотности окружного армирования µ⁰₂и различной плотности радиального армирования µ⁰₁: 0 (линия 1); 0.15 (2); 0.25 (3); 0.35 (4)

Рис. 6. Предельная угловая скорость вращения диска с радиально-окружной структурой армирования в зависимости от плотности радиального армирования µ⁰₁при r = R0 или r = R∗ (пояснения см. в тексте)

его части (R∗ ⩽ r ⩽ R1 , R0 < R∗ ), как изображено на рисунке 1г. В подобласти R∗ ⩽ r ⩽ R1 предположим радиально-окружное армирование и потребуем, чтобы в каждой точке этой подобласти суммарная плотность армирования µΣ была равна предельно допустимому значению µm (см. (2)):

Ms = Mi(r) +Mi(r) = Mm = 0.7,  R*< r< R1.

При этом плотность армирования м1 (r) по-прежнему будем определять равенством (24) (к = 1) при замене в нем R0 на R*, а величину M2(r) вычислять из соотношения (31) при известной из (24) функции M1 (r), причем под Mi в (24) понимаем плотность армирования, заданную на внутреннем контуре армированной подобласти (при r = R*). С учетом этого формула (30) принимает вид:

V2 = V2(m1) = nH [^e (Ri -R^-2R*(Ri -R*)m1].

Согласно формулам (21) и (31), в рассматриваемом случае армирования диска постоянной толщины H имеем выражение:

Vf = nH (R2-R^Ms.                                (32)

Из условия (26) при учете (32) и первого равенства (27) получаем:

R* =

1 IR2 -   (Ri-R2 =. I Ri -   (Ri-R2.

µΣ               µ_m

При заданных значениях R₀, R1, Mm и ^e (см. (22) и (31)) из выражения (33) следует R* = 16.66 см.

Таким образом, при известном значении R*, согласно формулам (24) (при k = 1) и (31), имеем однопараметрическое описание радиально-окружной структуры, зависящей от параметра µ⁰₁ — плотности армирования радиальным семейством волокон, заданного на контуре r = R*, причем ⁰< м1< Mm = 0.7.

На рисунке 6 кривые 2 и 2^′ отвечают зависимостям ω_mµ⁰₁ , рассчитанным для дисков с обсуждаемыми структурами армирования при отсутствии и наличии лопаток соответственно. По поведению кривой 2 видно, что для дисков без лопаток наибольшие значения ш_т достигаются при м1 = 0 (при окружном армировании) и на горизонтальном правом участке 0.3 < м1 С 0.7. В указанных точках кривой 2 предельно допустимая скорость вращения составляет: w_m = 3887 рад/с. Это значение существенно меньше ординаты левой точки на кривой 1 рисунка 5. Следовательно, для КМ-дисков без лопаток армирование только внешней подобласти полотна диска (R_∗ ⩽ r ⩽ R₁ ) является менее эффективным по сравнению с радиально-окружным армированием всей области R0 ⩽ r ⩽ R1 (см. кривые на Рис. 5 при 0 < м2 < 0.4).

Данное обстоятельство объясняется особенностями пластического течения полотна диска в его предельном состоянии. Так, крайней левой точке и точкам горизонтального участка на кривой 2 рисунка 6 в предельном состоянии КМ-дисков соответствует зависимость v(r), характеризующаяся кривой 7 на рисунке 3а. Как видно из поведения этой кривой, в предельном состоянии внешняя армированная подобласть (R∗ ⩽ r ⩽ R1 ) в таких КМ-дисках остается абсолютно жесткой, а пластическое течение, будучи стесненным, развивается только во внутренней неармированной подобласти (R₀⩽ r < R_∗). Поэтому для увеличения несущей способности рассматриваемых КМ-дисков подобласть R0 ⩽ r < R∗ необходимо дополнительно усиливать либо за счет увеличения толщины полотна диска H(r), либо за счет армирования этой подобласти.

Наличие убывающего участка на кривой 7 на рисунке 3а (13.0 < r < 16.66 см) свидетельствует о том, что в соответствующих точках диска из магниевого сплава МА2 в предельном состоянии реализуется наклонный режим пластического течения A2A3 (см. Рис. 2б). Поэтому, несмотря на то, что в рассматриваемых дисках структура армирования является радиально-окружной (см. Рис. 1г), для определения значений предельной угловой скорости их вращения нельзя прибегать к аналитическому решению (15) при учете (16), так как кривая 7 рисунка 3а не описывается зависимостью типа (18).

Как уже отмечалось в разделе 1, главная трудность при получении полного решения задачи о предельном состоянии вращающегося КМ-диска заключается в решении существенно нелинейного функционального уравнения относительно ω²(см. (18) в [9]). Для решения этого уравнения в [9] предложено применять процедуру продвижения по параметру, в качестве которого рекомендуется использовать радиус r∗ (R0 ⩽ r∗ < R1), определяющий границу между абсолютно жесткой подобластью (R₀⩽ r ⩽ r_∗) в предельном состоянии полотна диска, примыкающей к внутреннему контуру r = R0, и внешней подобластью его пластического течения (r∗ < r ⩽ R1 ). При этом продвижение по параметру r∗ предлагается проводить от внешнего контура R1 к внутреннему R₀. Такое направление продвижения по r_∗обусловлено введенным в [9] предположением, что в предельном состоянии в окрестности внешней кромки r = R1 в полотне диска всегда возникает подобласть пластического течения (r∗ < r ⩽ R1 ). Однако поведение кривой 7 на рисунке 3а (см. правый участок этой кривой при 16.66 < r ⩽ 19.75 см) свидетельствует о том, что при некоторых структурах армирования в предельном состоянии диска его внешняя подобласть, примыкающая к контуру R1 , может оставаться абсолютно жесткой. Следовательно, метод продвижения по параметру r∗ от внешнего контура R1 к внутреннему R0, предложенный в [9] для решения указанного выше нелинейного относительно ω²уравнения, в таких случаях не позволяет найти полное решение соответствующей задачи о несущей способности КМ-диска. Аналогичная ситуация может сложиться и в однородных дисках, если в окрестности их внешних контуров толщина полотна H (r) будет избыточно большой — тогда в предельном состоянии обод диска окажется абсолютно жестким.

Как уже отмечалось, левой точке на кривой 2 рисунка 6 (при µ⁰₁= 0) в предельном состоянии КМ-диска эпюра радиальной скорости течения в точках его полотна представляется кривой 7 на рисунке 3а. Точки правой части этой кривой имеют нулевые ординаты, поэтому при такой — окружной — структуре армирования внешней подобласти полотна диска (R∗ ⩽ r ⩽ R1 ) развивается стесненное пластическое течение его неармированной внутренней части (R0 ⩽ r < R∗). При увеличении же µ⁰₁от нуля до 0.15 на кривой 2 рисунка 6 наблюдается уменьшение значений ω_m. Это объясняется тем, что при µ⁰₁> 0 армированная подобласть полотна диска при соответствующих структурах (см. (24) и (31)) в предельном состоянии тоже течет, то есть пластическое течение полотна диска является менее стесненным, чем при µ⁰₁= 0. Так, при значениях µ⁰₁, близких к нулю, эпюры скоростей течения в точках полотна диска v (r) имеют вид, качественно аналогичный кривой 8 рисунка 3а, рассчитанной при µ⁰₁= 0.05. При этом в армированной подобласти скорости течения в предельном состоянии постоянны, но отличны от нуля (см. правый участок на кривой 8). При дальнейшем увеличении µ⁰₁эпюры v(r) становятся подобными кривой 6 рисунка 3а, а при значениях µ⁰₁, близких к 0.15 (см. минимум на кривой 2 на Рис. 6), эпюры v(r) совпадают с кривой 1 рисунка 3а. Таким образом, с ростом значений µ⁰₁от нуля до 0.15 в предельном состоянии пластическое течение таких КМ-дисков становится все менее стесненным, что и объясняет уменьшение зависимости ωm µ⁰₁при изменении плотности радиального армирования в интервале: 0 < µ⁰₁< 0.15. При последующем наращивании µ⁰₁от 0.15 до 0.3 наблюдается обратная картина: пластическое течение КМ-дисков в предельном состоянии становится все более стесненным, поэтому на интервале 0.15 < µ⁰₁< 0.3 зависимость ω_mµ⁰₁возрастает (см. поведение кривой 2 на Рис. 6). При значениях же 0.3 < µ⁰₁⩽ 0.7 армированная подобласть в КМ-дисках с соответствующими структурами в предельном состоянии вновь не течет, как и при µ⁰₁= 0. При этих значениях µ⁰₁зависимости v (r) принимают вид, аналогичный кривой 7 рисунка 3а, то есть пластическое течение таких КМ-дисков снова становится стесненным — пластическое деформирование испытывает только неармированная внутренняя подобласть полотна диска (R0 ⩽ r < R∗). Именно поэтому правый участок кривой 2 на рисунке 6 является горизонтальным. Этими же обстоятельствами объясняется и резкое уменьшение зависимости ωm µ⁰₁при 0.02 < µ⁰₁< 0.15, последующее ее нарастание при 0.15 < µ⁰₁< 0.6 и постоянство при 0.6 < µ⁰₁⩽ 0.7, наблюдаемое на кривой 2^′рисунка 6.

Правый участок кривой 2′ на рисунке 6 лежит существенно выше кривой 1′. Это означает, что при одной и той же массе и одинаковом расходе волокон диски с лопатками, в отличие от дисков без лопаток (см. выше), целесообразно армировать именно в окрестности внешнего контура (R∗ ⩽ r ⩽ R1 ). Правые горизонтальные участки кривых 2 и 2′ на рисунке 6 совпадают. Следовательно, в отличие от всех рассмотренных ранее случаев, при армировании дисков в окрестности внешнего контура с плотностью армирования 0.6 < м1 < 0.7 предельное значение угловой скорости их вращения одинаково как при наличии (кривая 2′), так и при отсутствии (кривая 2) лопаток. Объясняется это тем, что в обоих случаях при 0.6 < м1 < 0.7 пластическое течение в КМ-диске в предельном состоянии развивается только в неармированной подобласти (R0 < r < R*). И тогда зависимость v(r) качественно аналогична кривой 7 рисунка 3а. Дальнейшее увеличение несущей способности дисков с лопатками так же, как и в случае конструкций без лопаток, возможно за счет усиления внутренней подобласти диска (R0 < r < R*): либо изменения (увеличения) толщины его полотна H(r), либо армирования этой подобласти.

Выше исследовалось предельное состояние дисков с фиксированным относительным объемом арматуры Ω в них, равным эталонному значению Ωe (см. (22) и (26)). Теперь рассмотрим КМ-диски, в которых это условие не используется. Структура армирования дисков по-прежнему является радиально-окружной; армируется все полотно (R0< r< Ri) диска постоянной толщины H. Плотность армирования радиальным семейством m₁ (r) определяется по формуле (24) при k = 1, а плотность армирования окружным семейством зададим в виде:

M2(r) = Mi -Mi(r), Ro<r< Ri. (34)

При этом суммарная плотность армирования

Ms = Mi(r)+M2(r) = Mi (Ro<r< Ri) (35)

постоянна и равна m1 (см. (24)). При m1 = 0 получаем изотропный диск из сплава МА2. Для каждого значения Mi G [0,0.7] его толщину H по-прежнему задаем такой, чтобы его масса (23) имела эталонное значение me (см. (17)).

На рисунке 6 штриховая кривая 3^′отвечает зависимости ωm µ⁰₁ для таких КМ-дисков с лопатками. Аналогичная кривая 3 для КМ-дисков без лопаток на рисунке 6 не показана, чтобы не загромождать его: эта кривая, как и кривая 3‘, монотонно растет, причем для кривой 3 имеем wm(0) = 2519 рад/с и wm(0.7) = 7325 рад/с (см. первую и седьмую строки Табл. 1 при M = 201). Обе кривые можно рассчитать и аналитически (по формуле (15) с учетом (16)).

Из всех рассмотренных ранее структур армирования с фиксированным значением Q = Qe (см. (22) и (26)) наибольшую несущую способность дискам без лопаток обеспечивает окружная структура (m₁ (r) = 0) с линейным возрастанием плотности армирования м2 (r) от внутреннего контура R0 к внешнему R_i при значении m2 = 0 (см. левую точку на кривой 1 рисунка 5). В этом случае имеем: w_m = 4669 рад/с. Использование же радиально-окружной структуры армирования, для которой выполняются соотношения (34) и (35) с учетом (24)(к =1), позволяет при м1 = 0.7 получить предельно допустимое расчетное значение угловой скорости вращения диска без лопаток, равное w_m = 7325 рад/с, что на 57% больше значения w_m = 4669 рад/с. Однако при этом в диске со структурой армирования, обладающей свойствами (34) и (35), при м1 = 0.7 относительное объемное содержание волокон составляет П = 0.7, что в 3.25 раза больше, чем в КМ-дисках с эталонным значением П = Qe (см. (22) и (26)).

В случае КМ-дисков с лопатками ситуация иная. Так, правый участок кривой 2^′на рисунке 6 лежит выше кривой 3‘. Следовательно, армирование полотна диска с лопатками в окрестности его внешнего контура r = R_i (см. Рис. 1г) по-прежнему является более эффективным, чем армирование всей области, занимаемой диском (см. Рис. 1 в), даже несмотря на то, что при Mi = 0.7 (см. правые точки на кривых 2‘ и 3‘ на Рис. 6) относительный расход волокон в дисках со структурой, обладающей свойствами (34) и (35) (Q = 0.7), более чем втрое превосходит относительный расход арматуры в дисках, усиленных волокнами лишь в окрестности внешнего контура r = R_i ив которых Q = Qe.

Таким образом, для достижения наибольшего значения угловой скорости вращения дисков без лопаток целесообразно армировать все полотно диска (R₀ ⩽ r ⩽ R₁ ) по радиальным и окружным направлениям с использованием формул (34) и (35) при учете (24) (к = 1) и м1 = Mm. Диски же с лопатками целесообразно наиболее интенсивно армировать в окрестности внешнего контура (R* < r < R_i, Rq< R*) также при m1 = Mm.

Ординаты точек на левых участках кривых на рисунке 5 (при 0 < м2 ^ 0.3) и значения wm, приведенные в таблице 1 для КМ-дисков без лопаток, существенно превосходят величины ωm из таблицы 1 для таких же однородных и изотропных дисков из магниевого сплава МА2 и стали марки 35ХГСНА. Аналогично, ординаты точек на правом горизонтальном участке кривой 2^′рисунка 6 существенно больше значений ωm, приведенных в таблице 1 для однородных и изотропных дисков с лопатками. Следовательно, рациональное армирование дисков как с лопатками, так и без лопаток позволяет значительно увеличить их предельную скорость вращения даже по сравнению с высокопрочными стальными дисками той же массы.

• 6.    Заключение

Численно решена задача определения верхних значений предельных угловых скоростей вращения плоских композитных дисков с лопатками из жесткопластических материалов при квазистационарных режимах вращения. Полотно дисков армировано в радиальном, окружном и радиально-окружном направлениях или по спиральносимметричным траекториям двумя семействами волокон. Компоненты композиции могут иметь разные пределы текучести при растяжении и сжатии, а материал связующей матрицы может обладать цилиндрической ортотропией. Механическое поведение композиции описывается структурной моделью, учитывающей сложное напряженное состояние во всех фазовых материалах. При этом кривые текучести компонентов композиции в главных напряжениях в условиях предполагаемого обобщенного плоского напряженного состояния являются кусочно-линейными. Для решения предельной задачи сформулирован экстремальный принцип и разработан численный алгоритм его дискретизации. Численное решение разыскивается с использованием методов линейного программирования.

Для однородных и изотропных дисков из традиционных конструкционных материалов и для композитных дисков с радиально-окружной структурой армирования продемонстрирована сходимость численного решения, причем с хорошей точностью, к аналитическому решению, полученному ранее в [9].

Исследовано влияние параметров армирования на предельное значение угловой скорости вращения дисков при следующих видах укладки арматуры: по прямолинейным траекториям (геодезическим линиям), по логарифмическим спиралям, по радиально-окружным направлениям. Проведенные расчеты показали, что при условии одинакового относительного объема волокон и одной той же массы у дисков при отсутствии лопаток предельная угловая скорость их вращения слабо зависит от углов армирования по логарифмическим спиралям. Такая же слабая зависимость наблюдается и для дисков как с лопатками, так и без лопаток, армированных прямолинейно под разными углами к радиальному направлению на их внутреннем контуре. Несущая же способность дисков с радиально-окружной структурой армирования существенно зависит от распределения плотностей армирования волокнами разных семейств.

При спиральной укладке волокон (в частности по геодезическим линиям) наибольшее значение предельной угловой скорости вращения развивают диски, армированные по радиальным направлениям или близким к ним. Значительно большей несущей способностью обладают диски с радиально-окружной структурой армирования.

Показано, что в случае конструкций без лопаток наибольшую предельную угловую скорость вращения имеют диски с радиально-окружной структурой, у которой суммарная плотность армирования постоянна (не зависит от полярного радиуса) и равна максимальному, предельно допустимому значению. В случае же дисков с лопатками для получения наибольшей несущей способности их необходимо наиболее интенсивно армировать по радиальным и окружным направлениям в окрестности внешней кромки (к которой прикреплены лопатки) с максимально допустимой плотностью армирования в радиальном направлении при постоянной суммарной плотности армирования в этой подобласти. Дополнительно можно повысить несущую способность вращающихся дисков за счет их рационального профилирования — рационального изменения толщины их полотна вдоль полярного радиуса, как это традиционно принято делать для дисков из однородных конструкционных материалов [1, 19].

Показано, что при некоторых структурах в предельном состоянии диска в окрестности его внутреннего контура может появиться абсолютно жесткая армированная подобласть. Такая же жесткая подобласть может возникнуть и в окрестности внешнего контура при усилении волокнами полотна диска только в этой подобласти. В случае композитных дисков с лопатками в их предельном состоянии часто наблюдается пластическое течение только в бесконечно малой (по полярному радиусу) окрестности внешней кромки — в месте потенциального отрыва замковой разрезной части диска вместе с лопатками от его полотна.

Продемонстрировано, что рациональное армирование дисков как с лопатками, так и без лопаток позволяет значительно увеличить их предельную скорость вращения по сравнению даже с высокопрочными стальными дисками той же массы.

Находимые численно верхние значения угловых скоростей вращения дисков могут служить начальным приближением для построения полных решений соответствующих задач о предельных состояниях дисков [9]. Даже если кривые текучести компонентов композиции не являются кусочно-линейными, то при их аппроксимации с приемлемой точностью кусочно-линейно и решении численно возникающей при этом экстремальной задачи полученное в результате значение угловой скорости вращения диска также можно использовать как нулевое приближение при построении полного решения с целью отыскания его несущей способности [9].

Работа выполнена в рамках государственного задания (№ госрегистрации 121030900260-6).