Численный метод расчета мест размещения ретрансляторов систем безопасности на местности с препятствиями
Автор: Старцев Д.Ю., Логинов И.В., Сосунов В.Г., Плыгунов О.В.
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Радиопередающие и радиоприемные устройства, телевидение
Статья в выпуске: 1 (81) т.21, 2023 года.
Бесплатный доступ
При развертывании временных технических систем безопасности в интересах обеспечения общественной безопасности при проведении массовых мероприятий широко используют быстроразвертываемые датчики обнаружения опасных событий: наблюдения за транспортными потоками и посетителями, обнаружение возгораний, драк, агрессивного поведения, опасных оставленных предметов, беспилотных летательных аппаратов. Ряд важных ограничений, среди которых геометрические размеры зон установки детекторов и ретрансляторов, пропускные способности каналов передачи данных, наличие запретных зон и высокая скорость передачи данных от современных датчиков опасных событий показывает необходимость рационального размещения ретрансляторов. В рамках решения этой задачи предложен алгоритм расчета мест размещения ретрансляторов на местности с препятствиями. Итеративный алгоритм расчета мест размещения позволяет найти точки установки ретрансляторов для обеспечения передачи высокоскоростных потоков данных мониторинга.
Ретранслятор, метод, положение, координаты, расстояние, система безопасности, радиосвязь, информационный поток, детектор
Короткий адрес: https://sciup.org/140303624
IDR: 140303624 | УДК: 004.75 | DOI: 10.18469/ikt.2023.21.1.07
Текст научной статьи Численный метод расчета мест размещения ретрансляторов систем безопасности на местности с препятствиями
При проведении массовых мероприятий с большим количеством людей на различных объектах, слабо оборудованных, либо совсем не оборудованных стационарными техническими средствами обеспечения безопасности и соблюдения правопорядка (городские площади, парки, стадионы и др.), возникает необходимость в развертывании временных технических систем безопасности. Для этих целей широко используются быстроразвертываемые детекторы обнаружения опасных событий, позволяющие: осуществлять наблюдение за транспортными потоками и посетителями; обнаруживать возгорания, драки, агрессивное поведение, опасные предметы, оставленные без присмотра, изменения химического и радиационного фона, беспилотные летательные аппараты и др. Передача информации от таких датчиков в центр управления безопасностью осуществляется по радиоканалу, при этом скорость передачи данных от одного датчика может достигать 10-30 мбит/с. В связи с этим возникает необходимость обеспечения непрерывной надежной радиосвязи для гарантированного получения сигналов наблюдения и тревожных событий, что приводит к необходимости развертывания сети радиосвязи, включающей в свой состав значительное число ретрансляторов [1].
Наличие ряда важных ограничений, основными из которых являются: геометрические размеры зоны размещения детекторов; пропускные способности каналов связи; наличие запретных зон размещения и высокая скорость передачи данных от современных датчиков обуславливает необходимость рационального размещения ретрансляторов при развертывании временных технических систем безопасности. При этом, единого решения, которое бы учитывало, как характеристики датчиков, так и параметры системы передачи данных для условий высокой закрытости местности в настоящий момент не разработано, что показывает актуальность разработки численных методов размещения ретрансляторов систем безопасности на местности.
Формальная постановка задачи размещения ретрансляторов на местности
Исходными данными для решения задачи размещения ретрансляторов технической системы безопасности на местности выступает план временно развертываемой технической системы безопасности [2]. План системы на местности разрабатывается заранее. Указываются места размещения высокоскоростных детекторов с точностью не менее 0,1 м. В общем случае известно следующее (пример – рисунок 1):
– множество строений (сооружений). Они представляют собой препятствия для распространения сигнала и запретные места для расстановки ретрансляторов передачи данных. Моделируются множеством многоугольников с характеристиками ослабления сигнала (определяется типом сооружения):
Z = {Zj}, zj= {p Pi,-, Pi,-, Pi (Zj)}, / , где Zj - препятствие, pji - вершина многоугольника (препятствия), у - коэффициент ослабления радиосигнала в препятствии;
- множество запретных зон размещения ре- трансляторов, задаваемых многоугольниками: ZD = {zdj} , zdj = ({Pi,-,Pjt,-,Pi(zdj)} , где zdj - j-я запретная зона, Pi = ^xt, y^ - координаты вершины многоугольника запретной зоны, I – количество вершин многоугольника;
– множество высокоскоростных датчиков и их отображение на карте (плане): D = { d j }, где d j - высокоскоростной датчик: d j = ( c j , P j ) , характеризующийся cj – потоком данных с датчика ( c d ~ 2..10 Мбит/с), и P j = Xxt , y ^ - координатами места размещения датчика;
– множество доступных ретрансляторов: Rs = { rsi}, где rsi = PP, D, где P - мощность передатчика, D – характеристики диаграммы направленности антенны.
Зона покрытия
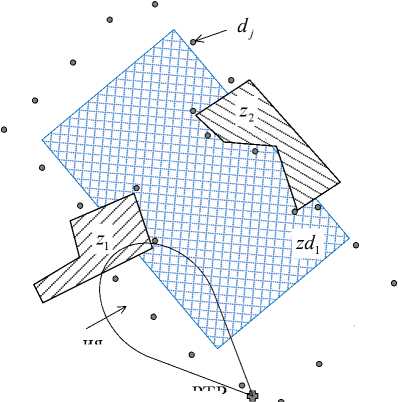
РТР
Рисунок 1. Пример исходных данных
Найти:
- подмножество установленных ретрансляторов RsP с Rs , где rsP = ( rs , p , Az^ , Az - направление (азимут) ретранслятора, p = ^ x i , y^ -координаты ретранслятора.
При выполнении следующего ограничения на размещение ретрансляторов:
||R^ H ^ min при ограничении:
CR (RSSI = min Rssikj. )а CND, где CR = C (RSSI) – максимальная пропускная способность k-го ретранслятора,
D ikm
ND ikm ij , ij ikm j=1
– суммарный поток пе-
редачи данных от всех высокоскоростных датчиков, подключенных к k -му ретранслятору rsPk (РТР).
Обзор подходов к решению задачи размещения объектов на местности
Общую постановку задачи на построение временно развертываемой системы безопасности и наблюдения и решение задачи оптимального размещения детекторов на местности рассматривали многие авторы: разработан алгоритм автоматизированного проектирования системы видеонаблюдения [3], эвристический алгоритм размещения, основанный на использовании диаграммы Вороного, покрывающий замкнутый многоугольник без дыр [4], эвристика замощения пространства геометрическими фигурами детектирования [2], в [5] решает задачу оптимизации размещения двумерных геометрических объектов на анизотропном материале с использованием методов математического программирования.
Известны исследования посвященные оптимизации размещения беспроводных терминалов [6–9]. В [6] рассматривается задача перепроектирования беспроводных сетей при изменении внешних условий на основе методов машинного обучения. В [10] рассмотрено размещение датчиков температуры. В [7] предлагаются основанные на UWB коммуникационные протоколы для расчета местоположения беспроводных сенсоров. Применяется метод, основанный на ортогональном переменном коэффициенте распространения и скачке времени, методе оценки максимального правдоподобия для вычисления расстояний до опорных сенсоров, учитывающий координаты подвижных сенсоров с использованием метода наименьших квадратов. В [8] предлагается новый алгоритм, позволяющий точно находить лучшие местоположения беспроводных датчиков при минимизации средней потребляемой энергии в сети. Оптимизация проводится по критериям стоимости и качества связи.
Задача размещения объектов на местности с ограничениями может быть представлена как за- дача покрытия многоугольника с препятствиями некоторыми фигурами (для ретранслятора это область одного уровня сигнала с заданной гарантированной пропускной способностью). Указанного рода задачи нашли распространение в нескольких отраслях науки и техники: в астрономических исследованиях решается задача покрытия кругами плоскости; в системах видеонаблюдения решается задача покрытия треугольниками или секторами; в системах транспортного мониторинга рассматривается задача покрытия территории кругами областей действия RFID-считывателей; для химических исследований используется задача покрытия шарами заданной трехмерной области; при строительстве дорог используется покрытие плоскостей плитами различной геометрической формы; в системах виртуальной реальности решают задачи генерации карт вейпоинтов [11]. Общие классы решения задач данного вида включают [12]:
– задачи компоновки объектов в контейнеры (двух и трехмерные) [13]: элементов печатных плат, грузов, коробок, товаров [14; 15];
– задачи оптимального раскроя материалов, решаемые в машиностроении, текстильной и авиастроительной промышленности, при этом заготовки могут быть произвольной формы;
– задачи распределения ограниченных ресурсов различных типов: память вычислительных машин, участки полей и лесов [16].
Все рассмотренные выше классы задач относятся к задачам оптимизационного геометрического моделирования, заключающегося в оптимизации размещения объектов произвольных измерений в заранее заданных областях [17–21]. При этом в известных решениях не показано использование покрытия области фигурами, имеющими вид диаграмм направленности антенн с учетом ограничения количества устройств и мест их размещения.
Модель ретранслятора
Во временно развертываемых системах безопасности используются сети связи, организованные на основе технологий Wi-Fi, WiMAX, 3G, 4G, 5G. В работе, независимо от общности рассматриваемых вопросов размещения ретрансляторов, дальнейшие рассуждения приведены для технологии Wi-Fi, которая позволяет обеспечить передачу данных со скоростью 1000 – 50 Мбит/с на расстояние до 100-300 м.
Технология IEEE 802.11 (Wi-Fi). Для построения беспроводных сетей, как правило, применяют беспроводные клиентские устройства (адаптеры), точки доступа, беспроводные маршрутизаторы, повторители, мосты и антенны.
Исходные данные для решения поставленной задачи целесообразно разделить на две группы – данные, позволяющие определить минимально необходимый уровень мощности сигнала на входе датчика для обеспечения радиосвязи, и план временно развертываемой технической системы безопасности.
С точки зрения расстановки ретрансляторов необходимо учитывать, что распространение радиоволн в сложных условиях связаны с явлениями многолучевости, обусловленной многократными отражениями радиоволн от стен и объектов, а также дифракцию на многочисленных острых кромках предметов и рассеяние при столкновении радиоволн с препятствием соизмеримым с длиной волны. Данные эффекты обуславливают сложную структуру электромагнитного поля. Поэтому в каналах беспроводной связи возникают затухания сигналов двух типов – крупномасштабное и мелкомасштабное.
Крупномасштабное затухание показывает среднее ослабление мощности сигнала из-за распространения на расстояние, определяется наличием вдоль траектории распространения таких объектов как: строения, растительность, рекламные щиты, стены, двери, перекрытия зданий и т. д. Таким образом, потери на пути распространения радиосигнала при крупномасштабном затухании можно рассчитать, как функцию от расстояния. В этом случае мощность принимаемого сигнала уменьшается с расстоянием по степенному закону, а отклонения от среднего значения определяются логарифмически нормальным распределением [22].
Мелкомасштабное затухание обусловлено вариациями амплитуды и фазы сигнала, и проявляется как расширение сигнала во времени и нестационарное поведение частотного канала связи. В системах беспроводной связи параметры канала изменяются во времени, в том числе и из-за движения передатчика или приемника. Мелкомасштабное затухание называется релеевским, если прямая видимость между передатчиком и приемником отсутствует, а сигнал в точку приема приходит в результате многократных отражений от различных объектов. Огибающая такого сигнала моделируется релеевской функцией плотности вероятности. Преобладание прямой видимости при распространении сигнала позволяет описать огибающую мелкомасштабного затухания функцией плотности вероятности вида Райса. Этот вид затухания вносит значительный вклад в затухание в каналах мобильной связи из-за того, что распространение сигнала происходит на большие расстояния. В случае же распростране- ния Wi-Fi сигнала на незначительных территориях этим видом затухания можно пренебречь, обеспечив на линии некоторый энергетический запас. Таким образом, при решении поставленной задачи представляет интерес не вычисление точной интенсивности (ослабления) сигнала, а некоторая его оценка, ввиду сложности учета деталей строений и, следовательно, всех особенностей мелкомасша-табного затухания.
С учетом сказанного для определения величины крупномасштаного затухания воспользуемся известной формулой:
L = 20 ■ X ■ 1g ( ^ f- ) , ( c )
где X – коэффициент ослабления, равный 1 для открытого пространства, d – расстояние до детектора, f – частота радиосигнала, с – скорость света.
При этом минимально необходимое значение уровня принимаемого сигнала датчика во многом определяется передающей и приемной антеннами.
Типовая диаграмма направленности наиболее распространенных антенн, используемых для передачи сигнала по радиоканалу, представлена на рисунке (рисунок 2).
Исходя из вышеизложенного, для решения поставленной задачи с учетом известных потерь ( L ), коэффициентов усиления передающей и приемной антенн ( G1 , G2 ) и мощности передачи точки доступа ( P1 ) можно определить минимально необходимый уровень мощности принимаемого сигнала ( RSSI ):
RSSI = P 1 ■ G 1 ■ G 2 ■ L .
При этом следует полагать, что потери в фидере для точки доступа будут незначительны, и их можно не учитывать, а в целях устойчивого функционирования радиолинии следует ввести запас уровня сигнала на входе приемника.
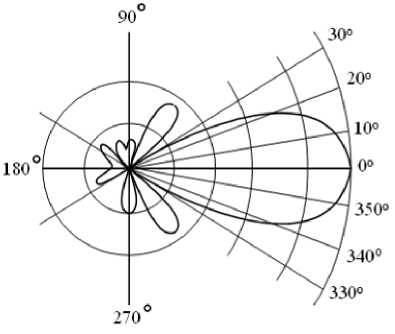
Рисунок 2. Типовая диаграмма направленности антенн
В общем случае пропускная способность радиоканала от датчика до ретранслятора определяется модуляцией и кодированием сигнала (рисунок 3) и зависит от наличия прямой видимости, мощности передаваемого сигнала, используемого диапазона частот, коэффициента усиления антенны и количества информационных потоков, а также от вида используемой модуляции. Значение пропускной способности ретранслятора может быть представлено в виде функции от уровня сигнала в точке наихудшего приема сигнала (определяется таблично в зависимости от технологии передачи данных:
C R = С ( RSSI ) .
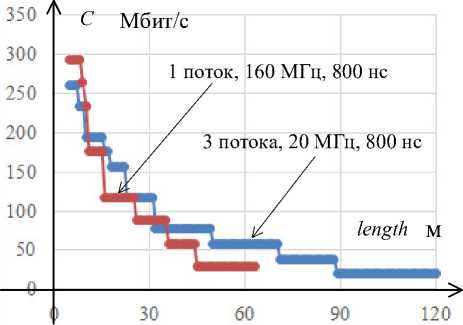
Рисунок 3. Пропускная способность от дальности до точки для Wi-Fi 802.11n/ac
В соответствии с рекомендацией МСЭ-R M.1851-1 примером диаграммы направленности может служить косинус-квадратная антенна со следующими характеристиками:
– относительная форма распределения поля: f ( а ) = cos2 ( л-а/ 2 ) ;
– диаграмма направленности:
z х п 2 Г sin ц
F(ц ) = ;ц IТц J ’ п- 83,2 - sin О где ц =-----------, О — ширина луча по уров-
О 3 3
ню половинной мощности сигнала, О - направление на рассматриваемую точку.
В качестве приемной антенны целесообразно использовать штыревую антенну, коэффициент усиления которой составляет порядка 2–3 дБ.
Алгоритм расчета мест размещения ретрансляторов
Алгоритм определения мест размещения ретрансляторов представлен на рисунке 3. На первом шаге определяется минимальное количество ре- трансляторов с учетом совокупного потока данных от всех детекторов к k-му ретранслятору rsPk :
D ikm
Ckm = ^ c ij , c ij Е Dikm ’ j = 1
При этом все множество детекторов разбивается на равные по размеру подмножества Dk таким образом, чтобы расстоянием между двумя наиболее удаленными детекторами для каждого подмножества было минимальным:
NR
D = U Dk, к =1
где Dk – k-е подмножество детекторов NDi , max length (dt, d) ^ min , Dk ij length(d, dj) - смещенное на диаграмму направленности антенны евклидово расстояние между двумя детекторами:
, я V ( x j - x ) + ( y у ) 2 .
length(di, d}) =---------— -------- f(a)
Начальное количество ретрансляторов рассчитывается по формуле:
NR = Г CD /С ( RSSI (max length ( ND )) )" | .
С использованием алгоритма (рисунок 4) формируется исходное (новое) размещение ретрансляторов: Rs m = { rs j } m .
Для нового размещения ретрансляторов генерируется новое m-е разбиение подмножества детекторов Dk :
NR
D = 1 Id . im ikm к=1
Рассчитывается пропускная способность ретранслятора C km = С ( RSSI ) на основе значения RSSI ( d i km ) всех детекторов, замкнутых на i-й ретранслятор.
По всем сравниваются значения необходимой и имеющейся пропускной способности и прове- ряется условие:
V rsP, Е RsP mm : C Rm > C D. ■ 0)
При выполнении условия (1) работа алгорит- ма завершается, в противном случае генериру- ется новое размещение путем сдвига координат ретрансляторов против градиента (рисунок 6). При расчете новой пропускной способности сети передачи данных рассчитывается нехватка пропускной способности:
R
^ ^ = C km
^
ND C km
которое сравнивается с потоком данных от одного детектора £c = c ij . При нехватке ресурса добавляется дополнительный ретранслятор и генерируется новое размещение.
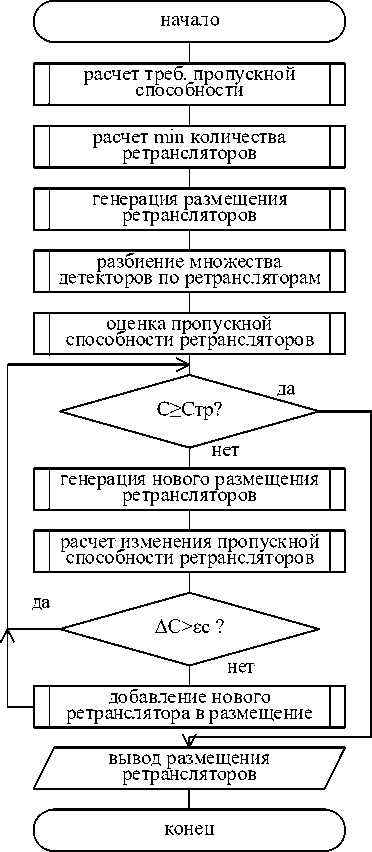
Рисунок 4. Блок-схема алгоритма расчета мест размещения ретрансляторов
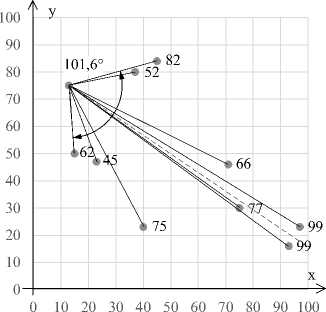
Рисунок 5. Иллюстрация расчета смещенного расстояния (n=10)
Пример нахождения смещенного на диаграмму направленности антенны евклидова расстояния между детекторами приведен на рисунке 5. Задано 10 детекторов, с одним из них совмеща- ется ретранслятор, и рассчитывается значение функции length(di, d j) для всех детекторов.
|
начало |
|
ввод размещения |
|
/ ретранслятора rsP o j |
Нахождение левого и правого детекторов dl dr
Расчет смещенного расстояния length
>1
Расчет биссектрисы
|
1 |
|
Расчет сдвига sdv |
|
Расчет новых координат ретранслятора rsPk |
||
|
1 |
||
|
Нахождение левого и правого детекторов dl dr |
||
Расчет смещенного расстояния length
Расчет расстояния сдвига
Рисунок 6. Итеративный алгоритм нахождения местоположения ретранслятора
Итеративный алгоритм нахождения рационального местоположения ретранслятора приведен на рисунке 6.
Исходные данные:
rsP = { x 0; у 0 } - точка местоположения ретранслятора;
D k
D k = U ^ j — множество детекторов, подсоеди- j = 1
ненных к ретранслятору.
Найти: rsP k = { x 0,k ; y 0,k } - точку размещения ретранслятора, такую, что max length ( rsP k , d j ) ^ min .
Основная идея алгоритма – использовани градиентного метода оптимизации. Первоначаль ная величина сдвига равна 1/10 от евклидовог расстояния до детектора. При возрастании теку щего значения смещенного расстояния, величин сдвига уменьшается в два раза. При попадании препятствие (запретную зону) – сдвиг выполня ется по границе запретной зоны в сторону убыва ния смещенного расстояния.
Критерий останова: сдвиг меньше 0,1 м ил изменение смещенного расстояния меньше (определяются точностью позиционирования ре транслятора на местности).
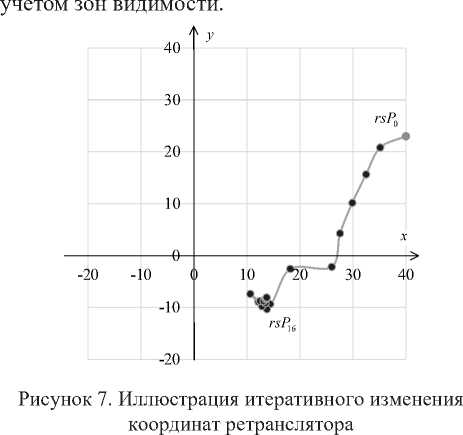
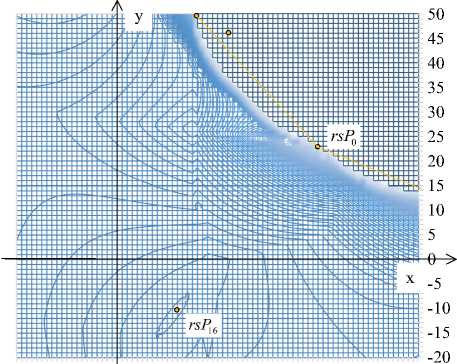
Пример: исходное положение детекторов приведено на рисунке 5. Начальное расположение ретранслятора совпадает с детектором: d = { 40; 23 } . Итоговое расположение ретранслятора после 16 итерации: d = { 13; - 8 } .
Вычислительная сложность и сходимость алгоритма: количество итераций основного алгоритма (рисунок 4) не превышает количества детекторов, количество итераций алгоритма размещения ретранслятора (рисунок 6) на практике составляло 30-70. Все расчеты имеют линейную сложность, соответственно, худший случай квадратично завит от числа детекторов.
Пример расчета мест размещения ретрансляторов
Для автоматизации подготовки данных по расстановке ретрансляторов разработано программное средство, позволяющее для заданных исходных данных (местоположения детекторов и интенсивности информационных потоков) рассчитывать местоположение ретрансляторов с
-20 -14 -8 -2 4 10 16 22 28 34 40 46 52 58
Рисунок 8. Значения целевой функции maxlength(rsPk, d j)
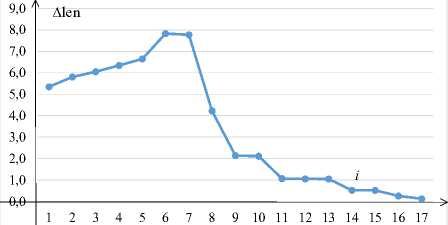
Рисунок 9. Изменение величины сдвига от итерации алгоритма
Вариант расчета местоположения ретрансляторов приведен на рисунке 11 и 12.
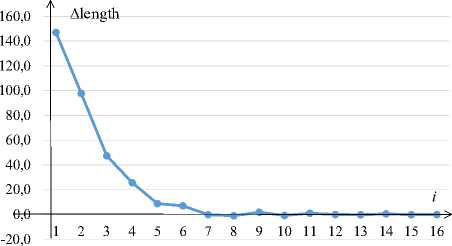
Рисунок 10. Изменение величины смещенного расстояния от итерации алгоритма
Вариант 2 расчета местоположения ретрансляторов приведен на рисунке 3 (режим 2).
Результаты выполненных с использованием алгоритма (рисунок 4) расчетов для различных исходных данных показали возможность нахождения минимального количества ретрансляторов и мест их установки для заданной конфигурации высокоскоростных датчиков.
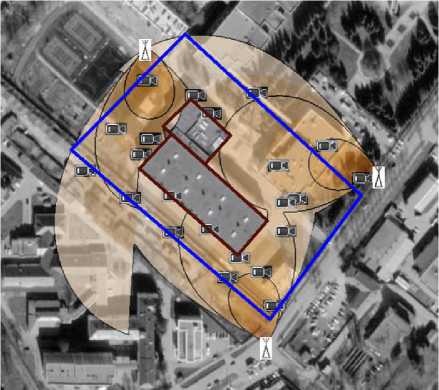
Рисунок 11. Пример размещения ретрансляторов (22 детектора, 3 ретранслятора)
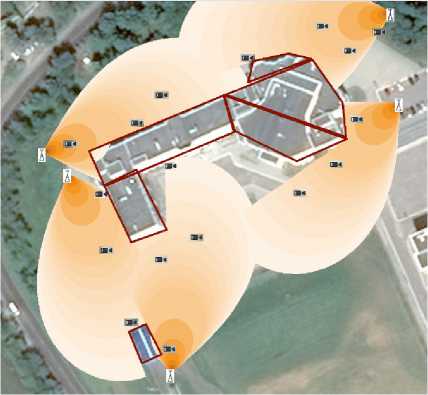
Рисунок 12. Пример размещения ретрансляторов (17 детекторов, 5 ретрансляторов)
Заключение
В работе рассмотрена проблема обеспечения непрерывной надежной радиосвязи для получения сигналов наблюдения и тревожных событий во временно развертываемых системах безопасности. В рамках решения этой задачи предложен алгоритм расчета мест размещения ретрансляторов на местности с препятствиями. Итеративный алгоритм расчета мест размещения позволяет найти точки установки ретрансляторов для обеспечения передачи высокоскоростных потоков информации мониторинга.
Список литературы Численный метод расчета мест размещения ретрансляторов систем безопасности на местности с препятствиями
- Логинов И.В., Старцев Д.Ю., Саламатов С.К. Оптимальное размещение сети видеокамер с радиоканалом в быстровозводимых системах мониторинга и охраны объектов // Вопросы оборонной техники. Серия 16: Технические средства противодействия терроризму. 2021. № 5–6 (155–156). С. 105–112.
- Логинов И.В., Старцев Д.Ю. Алгоритм оптимального размещения беспроводных видеосенсоров в быстровозводимых системах мониторинга и охраны объектов // Информационные системы и технологии. 2021. № 5 (127). С. 39–49.
- Лукоянов С.В., Белов С.В. Процедура рационального расположения камер видеонаблюдения в составе системы контроля и управления доступом // Вестник Архангельского государственного технического университета. Серия: Управление, вычислительная техника и информатика. 2012. № 2. С. 82–87.
- Воронов А.А. Метод покрытия прямоугольниками объектов топологии микросхем, основанный на использовании обобщенной диаграммы Вороного // Объединенный институт проблем информатики НАН Беларуси. 2009. № 3. С. 367–375.
- Петренко С.В. Оптимизация размещения двумерных геометрических объектов на анизотропном материале с использованием методов математического программирования: дис. … канд. техн. Уфа, 2005. 115 С.
- Machine Learning in Wireless Sensor Networks: Algorithms, Strategies, and Applications / M.A. Alsheikh [et.al.] // IEEE Communications Surveys and Tutorials. 2014. Vol. 16, no. 4. P. 1996–2018.
- Di W.U., Lichun B.A. O., Renfa L.I. UWB-Based Localization in Wireless Sensor Networks // Communications, Network and System Sciences. 2009. no. 5. P. 407–421.
- Ouchitachen H., Hair A., Idrissi N. Optimal Placement of Sensors in Mission-specific Mobile Sensor Networks // TELKOMNIKA Indonesian Journal of Electrical Engineering. 2015. Vol. 16, no. 1. P. 191–199.
- Reddy G.P., Gerardine M. Optimal node placement in wireless sensor networks // International Journal of Engineering Science and Technology. 2011. Vol. 3, no. 2. P. 1124–1129.
- Gongsheng H., Pei Zh., Linfeng Zh. Optimal Location of Wireless Temperature Sensor Nodes in Large-scale Rooms // 13th international conference on indoor air quality and climate, indoor air. 2014. P. 895–902. DOI: 10.13140/RG.2.1.1897.2884.
- Сафонов А.А., Панфилов А.Н. Применение алгоритмов геометрического покрытия для решения задачи размещения RFID-оборудования // Вестник молодежной науки России. 2019. № 2. С. 39.
- Забелин С.Л., Фроловский В.Д. Разработка и исследование моделей, методов и алгоритмов для синтеза и анализа решений задач геометрического покрытия // Вестник Сибирского государственного университета телекоммуникаций и информатики. 2013. № 2. C. 42–53.
- Курейчик В.В., Глущенко А.Е. Многоуровневый подход для решения задачи трехмерной упаковки большой размерности // Известия Южного федерального университета. Технические науки. 2020. № 2 (212). С. 6–16.
- Валеева А.Ф., Тоцков И.Е. Решение задачи трехмерной упаковки // Комплексный анализ, дифференциальные уравнения, численные методы и приложения: материалы международной конференции. Уфа: ИМВЦ УНЦ РАН, 1996. С. 30–36.
- Верхотуров М.А., Верхотурова Г.Н. О задаче трехмерной упаковки объектов сложных геометрических форм // Роль геометрии в искусственном интеллекте и системах автоматизированного проектирования: материалы всероссийской научно-технической конференции. Улан-Удэ, 1996. С. 43–45.
- Гиль Н.И. Математическое моделирование нерегулярного размещения плоских геометрических объектов в системах автоматизации проектирования (теоретические основы, методы, приложения): автореф. … дис. тех. наук. Минск,1990. C. 32.
- Стоян Ю.Г., Яковлев С.В. Математические модели и оптимизационные методы геометрического проектирования. Киев: Наукова думка, 1986. C. 286.
- Dycknoff H. A typology of cutting and packing problems // European Journal of Operational Research. 1991. no. 44. P. 145–159.
- Gilmore P.C., Gomory R.E. A linear programming approach to the cutting stock problem // Operation Research. 1961. Vol. 9, no. 6. P. 849–859.
- Хасанов Р.И., Дяминова Э.И. Математическое и программное обеспечение размещения ортогональных объектов в многоугольной области на базе матричной технологии // Молодежный вестник Уфимского государственного авиационного технического университета. 2019. № 1 (20). С. 183–186.
- Sun Ya., Halgamuge S. Minimum-Cost Heterogeneous Node Placement in Wireless Sensor Networks // IEEE Access. 2019. Vol.7. P.17847–17858. DOI: 10.1109/ACCESS.2019.2894117
- Скляр Б. Цифровая связь. Теоретические основы и практическое применение. 2-е изд., исправленное. М.: Издательство Вильямс, 2007. 1104 с.


