Численный метод решения задач смешанного управления для систем леонтьевского типа

Системы леонтьевского типа являются частным конечномерным случаем уравнений соболевского типа. Задача оптимального управления для уравнений соболевского типа впервые была поставлена и исследована в работах Г.А. Свиридюка и А.А. Ефремова, например [1]. В этих первых работах было доказано существование единственного решения указанной задачи с начальным условием Коши для случаев относительной ограниченности и относительной секториально-сти оператора.

Исследованиям задач оптимального управления для линейных уравнений соболевского типа в случае относительно радиальных операторов посвящены работы В.Е. Федорова и М.В. Плехановой, например [2]. Подчеркнем, что в работах этих авторов используется подход, предложенный Г.А. Свиридюком в работе [1] и развитый в [3]. Затем, исследования задач оптимального управления для уравнений соболевского типа велись по ряду направлений. Достаточные условия разрешимости задачи оптимального управления для некоторых полулинейных уравнений соболевского типа с начальным условием Шоуолтера–Сидорова получены Н.А. Манаковой [4]. Исследованию задач оптимального управления для уравнений соболевского типа высокого порядка посвящены работы А.А. Замышляевой, например [5]. В работе М.А. Сагадеевой и Келлер А.В. [6] доказано существование и единственность решения задачи оптимального управления Шоултера–Сидорова для нестационарного уравнения соболевского типа с сильно ( L , p ) –радиальным оператором.

Вместе с тем системы леонтьевского типа (или алгебро-дифференциальные системы, или дифференциально-алгебраические системы) представляют самостоятельный научный интерес в связи с большим числом приложений в экономике [7], технике [8, 9], биологии [10] и др. Алгоритмы численного решения класса задач оптимального управления для систем леонтьевского типа были разработаны в [11]. Важную роль в этих алгоритмах играет начальное условие Шоуолтера–Сидорова, которое, с одной стороны, сняло требование согласования начальных данных (что было необходимо при использовании условия Коши и часто при большой размерности матриц оказывалось нереализуемым требованием), с другой стороны, оказалось в ряде приложений более естественным условием, чем условие Коши [12]. Построенные алгоритмы были применены как в численном исследовании указанных приложений [7–10], так и придали импульс новым исследованиям стохастических систем леонтьевского типа и стохастических сигналов [13, 14].

Задача смешанного управления для уравнения соболевского типа рассмотрена А.Ф. Исламовой в [15]. Будем рассматривать задачи смешанного управления для систем леонтьевского типа с функционалом, отличным от предложенного в работе [15], так как по мнению ав-

Математика

торов этой статьи введенный ими функционал имеет более естественный экономический смысл, что обеспечивает решение прикладных экономических задач. Более того, преимуществом рассмотрения задачи смешанного управления в сравнении с задачами стартового и оптимального управления является более гибкое регулирование управляющего воздействия.

Точное решение задач смешанного управления

Введем в рассмотрение пространства состояний и управлений:

H ¹ ( X ) = { x е L 2 ( (0; т ); X ) : x е L ₂ ( (0; т ); X ) } ;

U = HP ^{+ 1} ( Y ) = { и е L 2 ( (0; т ); Y ) : и ^{( p + 1)} е L 2 ( (0; т ); Y ) } , U ⁰ = Y .

Выделим в U и U ⁰ компактные и выпуклые множества допустимых управлений: U ad , U ^ . Рассмотрим задачу смешанного управления min    J ( и ₀, и )

( U 0 , U ^{) е U} 0d X ^U ad

J (и 0, и) = а ^ j Cx(q) (и 0, и, t)- Cx0 q)(t) dt + в ^ j Nqqu(q), и(q dt + Y U 011 ,(1)

u=00

для системы леонтьевского типа

Lx( t) = Mx (t) + у (t) + B и (t)(2)

с начальным условием Шоуолтера-Сидорова

[Rlm (M)]P+1 (x(0) - и0 ) = 0,(3)

где R ^ L (M) = ( ^ L - M) ^{- 1}L - правая L-резольвента оператора, функции x ( t ), и ( t ), у ( t ) лежат в гильбертовых пространствах X, U , Y соответственно, операторы L е L( X , Y ) (L( X , Y )-множество линейных непрерывных операторов, действующих из пространства X в пространство Y ), kerL Ф {0} и M е Cl(X ; Y ) (замкнутый оператор M:domM ^ Y с областью определения, плотной в X ), B е L( U , Y ), причем оператор M сильно (L, p )-радиален [3], при этом а + в + у = 1, 8 = 0,1, ..., p + 1, p е {0} u N, t е (0; т ), т е Ж ₊= { т е Ж, т >  0}, N _q е L( U ) - положительно определенные и самосопряженные операторы.

Определение 1. Тройку ( v ₀, v ( t ), x ( v ₀, v ( t ) ) ) е U^ X U_ad X X назовем решением задачи смешанного управления (1)–(3), если

J ( v ₀, v ) =      min      J ( и ₀, и ) ,

( и 0,и )е U° XUad где (v0,v(t),x(v0,v(t)))е U^ XUad XX удовлетворяют (2), (3).

В [16] доказано существование единственного решения задачи смешанного управления (1)(3), т.е. справедлива

Теорема 1. Пусть оператор M сильно (L, p ) -радиален, p е {0} и N . Тогда для любого у е H^{p + 1} ( Y ) существует единственное сильное решение ( v ₀, v ( t ), x ( v ₀, v ( t ) ) ) е U ^d X U ad X X для задачи смешанного оптимального управления (1)–(3).

Для численного исследования различных прикладных математических моделей, сводящихся к решению задач смешанного управления для систем леонтьевского типа (конечномерному аналогу уравнений соболевского типа), будем использовать пространства состояний и управлений:

X = H ¹ ( Ж n ) = { x е L ₂ ( (0; т );Ж n ) : 5 с е L₂ ( (0; т );Ж n ) } ;

U = H^{p + 1} ( Ж ⁿ ) = { и е L ₂ ( (0; т ); Ж n ) : и ^{( p + 1)} е L ₂ ( (0; т );Ж n ) } , U ⁰ = Ж n , выделяя в U и U ⁰ компактные и выпуклые множества допустимых управлений: U ad , U_a d . Пусть M и L - квадратные матрицы n X n , причем det L = 0, матрица M (L, p ) - регулярна ( 3 2 е C :det( 2 L - M) = 0 3 p е {0} и N равное нулю, если в точке ^ L-резольвента ( 2 L - M) ^{- 1} матрицы M имеет устранимую точку и равна порядку полюса в противном случае).

Используя результаты разрешимости задачи Шоуолтера-Сидорова для системы леонтьевского типа [3] и

Теорема 2. Пусть матрица M (L, p ) -регулярна, p е {0} u N , причем detM Ф 0 . Тогда существует единственное решение ( v ₀, v ( t ), x ( v ₀, v ( t ) ) ) е U ° x U ad x X - точка минимума функционала (4), а x ( v ₀, v ( t ) ) - сильное решение задачи (2), (3) и определяется формулой

x ( v 0 , v ( t ) ) = ^lim X k ( v 0 , v ( t ) ) = ^lim k ^+~             k ^+~

p _q

-k v 0 - X ( M ^{- 1}( I - Q k ) L ) M ^{- 1}( I - Q k ) ( y ( t ) + Bv ( t ) ) ⁽ q ) + q = 0

T

+ J ₀ R k Q k ( y ( s ) + Bv ( s ) ) d s

где

G       ^-1

Q k = ( kL LL ( M ) ) p ^{+ 1}, R k =

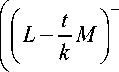
x k - 1

L

• ^f L - -M )

V k 7

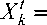
| ^{L -} 7^M | ^L

I    k)

V      v7

Сходимость. Свойства функционала

Рассмотрим функционал качества (1) на компактных выпуклых множествах U_ad с U , U 0 d с U ⁰. По построению функционал качества (1) является непрерывной функцией, на основании теоремы Вейерштрасса для непрерывных функций на компакте он будет ограничен на W ad = U ad x U d функцией. При исследовании на сходимость важным является свойство выпуклости функции.

Определение 2. Функция J ( w ) называется сильно выпуклой на выпуклом множестве A с H (H - гильбертово пространство), если для любых w ₁, w ₂ с A, для любого ю е [0,1] и для некоторого числа T >  0 выполняется неравенство

J ( m w₁ + (1 - m ) w ₂) <  m J ( w ₁) + (1 - m ) J ( w ₂) - m (1 - to ) Tw - w ₂||².

Теорема 3. Пусть матрица M (L, p ) -регулярна, p е {0} и N , det M Ф 0 , а множества

U ad с U, U ° с U ⁰ - компактны и выпуклы. Тогда функционал (4) является сильно выпуклой функцией на W ad = U ad x U ^ .

Доказательство. Рассмотрим выражение J( m w₁ + (1 - т )w ₂) для (1) и проведем тождественные преобразования

1 T                                                                          _||2

J(mw1 + (1 - т)w2) = аX J CX(q) (mw1 + (1 - m)w2,t)- Cx0q)(t) dt + q=00

+P XJ( N q ( m u 1 + (1 - m ) u 2 ) ⁽ q ) ( t ), (тц + (1 - m ) u 2 ) ⁽ q ) ( t )} dt + Y® u 01 + (1 - m ) u 02^ = q = 0 0

1 T..                                            _Il2                                 1 T                                               ₂

= a®X J|Cx(q) (w1, t) - Cx0q) (t) dt + а(т2 - m) X J | Cx(q) (w1, t) - Cx0q) (t) dt + q=0 0                                                q=0 0

+ a (1 - m ) X J| Cx ⁽ q ) ( w ₂, t ) - Cx 0 q ) ( t )| 2 dt + q = 0 0

+a((1 - m)2 - (1 - m)) X J|Cx(q)(w2,t) - Cx0q)(t)|2 dt + q=0 0

1 ^T

+ 2 am (1 - m ) X J Cxx ⁽ q ) ( w ₁, t ) - Cx 0 q ) ( t ), Cx ⁽ q ) ( w ₂, t ) - Cx 0 q ) ( t yj dt + q = 0 0

Математика

θτ                              θτ

+в«^ J( N q U q ) ( t ), u ( q ) ( t )) dt +в ( ®² - to ) E J\ N q U i q ) ( t )’ u ( q ) ( t C dt + q = 00                                          q = 00

θτ                                       θτ

+в(1 - to)E J(Nqu2q) (t), u2q) (t)) dt +в((1 - to)2 - (1 - to)) E J\Nqu2q) (t),u2q) (t)) dt + q=0 0                                                      q=0 0

θτ

+ 2 eto (1 - to ) EJ( N q u ( q ) ( t ), u ( q ) ( t C dt + q = 0 0

+ /to ² I| u 01 1|² + 2 Yto (1 - to ) { u 01 , u 02) + Y (1 - to ) ²1 \u 021|² = to J ( w ) + (1 - to ) J ( w 2 ) +

1 Tu

1 Т                             ii2

EJI Cx ⁽ q ) ( w 2 , t ) - Cx 0 q ) ( t )|| dt - q = 0 0

+(to2 - to) aEJ| Cx(q)(w1’ t) - Cx0q)(t) dt +a q=00

1 Т

-2a E J\Cx(q) (w1, t) - Cx0 q) (t), Cx(q) (w2, t) - Cx0 q) (tC dt + в E J \Nqu( q) (t), u( q) (tC dt + q=0 0

θτθτ

+вE J\Nqu2q)(t)»u2q)(t)/ dt - 2вE J \Nqulq)(t)’u2q)(t)/ dt + Y|u01 - u02|| q=0 0

T„

= to J ( w ₁ ) + (1 - to ) J ( w ₂ ) - to

¹ ( 1 - to ) a E J Cx ⁽ q ) ( w ₁, t ) - Cx ( w ₂, t ) dt +

_ q = 0 0

θτ

^{+ e} E J \ N q ( ^u 1 ⁽ q ) ⁽ t ) ^{- u} 2 q ) ⁽ t ) ) , “ 1 q ) ⁽ t ) ^{- u} 2 q ) ⁽ t )/ ^{dt + Y} I ^u 01 ^- u 02 II q = 0 0

Так как все слагаемые входящие в состав выражения в квадратных скобках неотрицательны и x ( w , t ) является непрерывной функцией при w е W_ad , то по теореме Вейерштрасса она будет ограничена на нем, а значит

J( to w₁ + (1 - to ) w ₂) <  to J ( w ₁) + (1 - to ) J ( w ₂) - to (1 - to ) r||w ₁ - w ₂||².

Теорема доказана.

Будем рассматривать задачу смешанного управления (1)-(3) при условиях (L, p )-регулярности матрицы M, p е {0} и N и detM ^ 0.

Обозначим (w, x(w, t)) точным решением, а (w^, Vck (wk, t)) - приближенное решение задачи смешанного управления.

Необходимо показать, что при k , I ^ ^ ( w k , x k ) ^ ( w , x ) так, что J k ( w k ) ^ J ( w ).

Лемма 1. Пусть матрица M (L,p) -регулярна, pе {0} и N, detM Ф 0, а функционал (1) является сильно выпуклой функцией на компактном и выпуклом множестве Wad с U0 х U . Тогда последовательность {w1} является минимизирующей, сходится к w по норме U при I ^ ^, при этом Jk (w1) ^ J(w) и выполняется неравенство q||w1 - w|| < J(w1) - J(w).

Доказательство. Множество W ad выпукло и компактно, следовательно, существует последовательность { W ad } выпуклых компактов W ad с W ad , монотонно исчерпывающих U д , т.е.

∞

W ad с W_a d ⁺¹, U W ad = W a _d . Из этого следует, что J ( w ^{l + 1}) <  J ( w ), а значит, для последова- i = p + 1

тельности {w1} с Wad существует предел lim J(w1) равный J(w) в силу непрерывности функ-ℓ→+∞ ционала (1). Таким образом, последовательность {w1} является минимизирующей.

Отметим, что по теореме Мазура компактное и выпуклое множество слабо компактное, т.о. W ad - слабо компактно. Тогда функционал (1) определен, ограничен на слабокомпактном множестве, а по теореме Вейерштрасса минимизирующая последовательность { w ¹ } будет слабо сходится к w .

Воспользуемся теоремой о сильной выпуклой и полунепрерывной снизу функции на выпуклом компактном множестве (или обобщением теоремы Вейерштрасса). Так как функционал качества (1) является сильно выпуклой и непрерывной функцией на Wad , последовательность {w1} -минимизирующая, а точка минимума w - единственна, следовательно, последовательность {w1} сходится при I ^ ^ к w по норме U так, что выполнятся неравенство q^w1 - w|| < J(w1) - J(w).

Лемма доказана.

Следствие 1. В условиях леммы 1 для задачи смешанного оптимального управления (1) - (3) последовательность { x ( w ¹ )} является минимизирующей, сходится к x ( w ) по норме X при ℓ →∞ .

Лемма 2. Пусть выполнены условия леммы 1, а функционал

Т,,2

Jk(v0, vk) = Jk(wk) = аЁ JICxkq)(wk, t) - Cx0q)(t)|| dt + q=oo e T„2

+ezj(Nq(vk)(q),(vk)(q)}dt +r|V0|| ,(6)

q=oo является сильно выпуклой и ограниченной функцией на выпуклом компакте Waℓd ⊂ Wad . Тогда последовательность {wk} является минимизирующей, сходится к w1 при k ^ ~ и фиксированном I > p по норме U, при этом Jk (wk) ^ J(w1) и выполняется неравенство q^wl- wl|| < Jk(wk) - J(w 1).

Доказательство. Так как J_k ( w k ) и J ( w ), определяемые формулами (6) и (4) соответственно, являются непрерывными и ограниченными на W ad функциями справедливо неравенство

|inf J k ( w k ) — inf J ( w )| <  sup | J k ( w k ) - J ( w )|.

Действительно,

^J k ^{( w} k ) = ^J k ^{( w} k ) ^{+ J ( w} ) ^{- J ( w} )>^suP ^J k ^{( w} k ) <  ^suP ^{J ( w} ) ^{+ su}P^{( J}k ^{( w} k ) ^{- J ( w} )), ^suP ^J k ^{( w} k ) ^{- su}P ^{J ( w} ) <  ^suP^{( J} k ^{( w} k ) ^{- J ( w} )), ^{- inf J} k ^{( w} k ) ^{+ inf J ( w} ) <  ^suP^{( J}k ^{( w} k ) ^{- J ( w} )), |^{inf J} k ^{( w} k ) ^{- inf J ( w} )| <  ^suP^{( J} k ^{( w} k ) ^{- J ( w} )) из чего получаем, что

| inf J k ( w k ) - inf J ( w )| <  £ .

Следовательно, последовательность { w k } является минимизирующей при k ^ ~ , сходится к w ¹ так, что J_k(w k ) ^ J ( w ¹ ) при фиксированном I >  p .

А так как функционал, определяемый (6) является сильно выпуклой и непрерывной функцией на выпуклом компактном множестве W ad , то по теореме о сильно выпуклой и полунепрерывной снизу функции на выпуклом замкнутом множестве последовательность { w k } сходится к w ¹ по норме в U и справедливо неравенство