Численный расчет оптимальной формы тела вращения при движении с постоянной скоростью в грунтовой среде

Проблема оптимизации процессов удара и проникания жесткого тела имеет давнюю историю. Рассматривались различные постановки и решения с выбором в качестве целевых функций оптимальных характеристик самого тела и / или формы преграды, заданием формы ударника и / или преграды с минимальным сопротивлением или максимальной глубиной проникания (см., например, [1–3]). Обзоры [4, 5] свидетельствуют, что большинство применяемых методов моделирования, и особенно посвященные решению задач оптимизации формы тела, основано на гипотезе локальности [5–16]. Постановка задачи с использованием различных модификаций моделей локального взаимодействия позволяет найти форму абсолютно-оптимального тела (АОТ) [6, 7] — тела, сопротивление которого при достаточно общих ограничениях зависит лишь от скорости его движения и свойств среды. Но задача поиска среди пространственных конфигураций той образующей, которая создает в классе АОТ материальный объект с заданной площадью основания и максимально допустимой длиной, может иметь бесконечно много решений [8]. Все такие тела являются коническими, то есть нормаль к поверхности тела составляет с направлением движения постоянный оптимальный угол, обуславливаемый скоростью тела и характеристиками грунта [9]. Использование гипотезы локальности при нахождении силы сопротивления внедрению в мягкий грунт острых конических и сферических тел продемонстрировано в работах [16–18].

Применение модификации модели локального взаимодействия для решения задачи расширения сферической полости [19–23] делает возможным учет динамической сжимаемости и сопротивления сдвигу грунтовой среды в рамках трех- или двухчленной по скорости модели, содержащей инерционное, вязкое и прочностное слагаемые [19, 20]. При высоких скоростях движения осесимметричные АОТ имеют значительное удлинение [8, 9]. Если заданная длина искомого тела меньше длины абсолютнооптимального конуса, то оптимальное тело, при отсутствии дополнительных ограничений на продольный контур [3], имеет притупление (плоский торец) [7, 10]. При превышении скоростью внедрения ударника значения скорости звука в грунтовой среде вклад вязкого и прочностного слагаемых уменьшается, контактное напряжение становится пропорциональным только квадрату скорости. В этом случае модель локального взаимодействия фактически содержит только один член, а форма оптимального тела не зависит ни от скорости его движения, ни от коэффициента модели [15]. Для определения радиуса торца и формы образующей оптимального тела необходимо прибегнуть к численным методам.

2.    Методика численного решения задачи

В цилиндрических координатах рассматривается стадия развитого проникания ударника длиной L и радиусом миделевого сечения r = R при постоянной скорости внедрения V 0 и условии, что обтекание искомой головной части ударника грунтом происходит безотрывно. Полное осевое сопротивление F проникающего тела описывается выражением [11]:

RR

F = с₀ R ² + 2 п J с n rdr + 2 п J

R 0 R 0

V1 -а2 --------с т rdr, а

а = sin п .

Здесь: первое слагаемое обусловлено напряжениями с₀ , действующими на передний плоский торец тела

радиусом R ₀ (Рис. 1), второе и третье слагаемые —

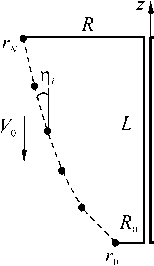
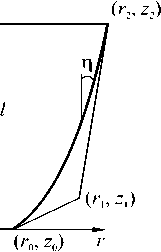
Рис. 1. Параметризация образующей искомого тела вращения

соответственно, нормальными ( с n ) и касательными ( с_т ) напряжениями, возникающими на боковой

поверхности тела. Напряжения с ₀ и с n описываются трехчленной квадратичной моделью локального взаимодействия: с n = Р о ( AVV + BVa + C ) , с о = Р о ( AV² + BV o + C ) ; касательные напряжения рассчитываются по закону Кулона с постоянной трения k_f : с_т = k f с _n . В модели р ₀ — плотность грунта, коэффициент A отражает вклад инерционных сил, параметры B и C связаны с характеристиками внутреннего трения и прочности грунта соответственно [19, 20].

Перейдем в выражении (1) к безразмерным величинам: D = F ( p ₀ V ₀ ² SA ) , ^с = ^с n /( P o V o ² A ) , r o = R о/ R,

l = L/R , B = B /( AV₀ ) , C = C /( AV ²), где S = n R ² — площадь миделя:

D(r) = (1 + 6 + C)r02 + 2j f (n)rdr,

r ₀

f (n)= 1 + k

Л-О2'n

(n2 + 6 n +

Необходимо отыскать такую выпуклую кривую r ( z ) , r ( l ) = 1, описывающую форму головной части ударника, чтобы полное сопротивление D имело минимум: D ( r ) ^ min.

Приближенное решение на основе известного метода локальных вариаций [24, 25] предполагает сведение исходной задачи к задаче безусловной оптимизации (см. также [12, 13, 26]), то есть к нахождению набора координат (r0,..., rN-1), который представляет собой такую кусочно-линейную выпуклую образующую тела вращения, при которой интегральная сила сопротивления внедрению D достигает минимума:

N

D ( r 0 ,..., r N - 1 H min, D = D 0 + E D i ,

D о = ( 1 + s + c ) r²,   D i

^{1 + k} тр

a ²

a i

( a 2

⁺ ? ^a i + C ) ( r ^{2 -} r i - i )

( i = 1, N),

где координаты zi распределяются по длине тела с шагом A z i , a i = sin n i = A r yA ² + A r² , A r = r - r- 1

(ii = 1, N ), T n = 1.

В работе [27] показана сходимость последовательных приближений при численном расчете формы оптимального тела и убывание погрешности определения силы сопротивления с ростом числа узлов образующей. Однако увеличение числа узлов свыше некоторого предела приводит к переполнению разрядной сетки и невозможности продолжения счета. Кроме того, алгоритм на основе кусочно-линейного представления образующей не имеет эффективного обобщения на случай расчета силы сопротивления внедрению при постановке задачи в рамках механики сплошных сред. В этой связи предпочтительнее рассматривать аппроксимации образующей в классе полиномов или степенных функций, содержащих небольшое число искомых параметров оптимизации [28]. Далее приводится модификация алгоритма из [27] с учетом указанных соображений.

Вектор неизвестных параметров r = { r i } ( i = 0, N - 1) сообщает функции (2) один из локальных экстремумов. Для их установления составляется система нелинейных уравнений

D ' ( r ) = { д D / д r } = 0 ( i = 0, N - 1).

Система (3) решается итерационным методом Ньютона, при этом используемые соотношения имеют вид

D "( r k ) ( r k ^{+ 1} - r k ) = - D ' ( r k ),

k

I d ² D I

D "( r k ) = J------I

15 r i d r j

,

где k — номер итерации, D"(rk) — симметричная матрица. Приращения компонент вектора координат на каждой итерации метода Ньютона (4) зависят от решения системы алгебраических уравнений с трехдиагональной матрицей дг д rj

A r j ^{+ 1}

—

д D

д r

k

A r j ^{+ 1} = r j ^{+ 1} - r j    ( i , j = 0, N - 1).

Выражения для компонент левой и правой частей системы (5) в случае кусочно-линейного представления образующей содержатся в [27]. В данной работе приводятся только их конечно-разностные выражения

5D = D+-D^+o(52},  ajD = D:-2D0+Di + O(52}, д r 25         ( )     д ri2           52             ( )

д2 D = D:+ D;- Dj -- 2 D0 - Dj ++D;+D: + O z52 x дr-дrj                          252                            ( ),

D0 = D(r0, .„, rN-1),    Di = D(r0, ^, r +5, ^, rN-1),    Dj- = D(r0, ^, r +5, -> rj -5, -> rN-1), где 5 — безразмерная вариация радиальной координаты; O (52) — порядок точности.

Счет осуществляется до выполнения условия

5 D ^{k + 1} = | D ^{k + 1} - D ^k |/ D ^{k + 1} < ₈ ,

где s — заданная точность.

Модифицированный таким образом алгоритм из [27] имеет единообразный порядок действий как при кусочно-линейном представлении образующей, так и при полиномиальном, когда компоненты вектора ( r ₀,..., r_N - 1 ) являются коэффициентами полинома. Для применения алгоритма необходимо также конкретизировать способ расчета интегральной силы сопротивления внедрению D в соотношении (2), поскольку для этого может использоваться как точный, так и приближенный метод вычисления интеграла. Заметим, что в общем случае симметричная матрица в уравнениях (4), (5) уже не будет трехдиагональной.

Рассмотрим для тела вращения с притуплением, имеющим радиус r ₀ , аппроксимацию образующей в форме параметрического полинома Безье второй степени [28]:

r ( 5 ) I z ^{( 5} ) )

= (1 — 5 ) 2

( F. 1                      { V X ( Г X

I r ⁰ л ad r i L<-2I ^r 2 I I 1 + 2 (1 ^— 5 ) 5      + 5        ,

V z 0 )             V z i ) V z 2 )

5 G [0, 1] .

С учетом поставленных ограничений — заданных значений радиуса основания и длины искомого оптимального тела, другие геометрические характеристики составляют r2 = 1, z0 = 0, z2 = 1. Вектор параметров r = {r0; r 1; z J содержит радиус притупления тела r0 и координаты вершины характеристического треугольника r1 , z1 (Рис. 1). Тогда выражение для силы сопротивления внедрению (2), при учете ограничений в представлении образующей (8), запишется следующим образом:

D(r) = (1 + Bi + C)r02 + 2j f (a)r(5)r'ds ,

где

r ( 5 ) = (1 — 5 )2 r0 + 2 (1 - 5 ) Sr + 5 2 , r‘ = -2 (1 - 5 ) r0 + 2 (1 - 2 5 ) r + 2 5 , z(5) = 2(1 - 5)5Z1 + 521, z' = 2(1 - 25)z1 + 2sl, a(5) = (1 + (z'/r')2)    .

3.    Анализ сходимости итерационного процесса

Для определения параметров квадратичной по скорости модели локального взаимодействия в работе применялась аппроксимация методом наименьших квадратов решения одномерной задачи расширения сферической полости в грунтовой среде, известного для диапазона скоростей проникания 100^400 м/с [21-23]. Значения параметров Ё = 0,17, б = 0,01 брались из [27] и соответствовали воздействию сухой песчаной смеси естественного состава. Коэффициент поверхностного трения принимался равным k f = 0,3. Безразмерная длина ударника составляла 1 = V5, скорость проникания — V , = 400 м/с.

Величина вариации параметров в конечно-разностных соотношениях (6) находилась при кусочнолинейном представлении образующей и 16 искомых узлах. Проводилось сравнение с результатами расчетов, проделанных с последовательным уменьшением 5 от 0,1 до 0,0001 (далее различие в координатах становилось несущественным); производные при этом отыскивались аналитически [27]. При вычислении параметров образующей в виде полинома Безье величина 5 принималась равной 0,0001.

Результаты расчетов приведены на рисунке 2, где маркеры « ○ » соответствуют решению системы уравнений (3) с кусочно-линейным представлением образующей, сплошная и пунктирная линии — численным решениям с представлениями в форме Безье, полученным при различных начальных приближениях в итерационном методе Ньютона (4), (5). Из них локальному минимуму функции (2) соответствует только образующая, изображенная сплошной линией (все угловые миноры матрицы вторых производных D" положительны). Вектор параметров этого решения имеет вид { r ₀ = 0,169; r ₁ = 0,498; z ₁ = 0,472 } . Другое численное решение { 0,141; 0,318; 0 } , изображенное пунктиром, локальным минимумом не является — угловые миноры матрицы D" имеют разные знаки, и значение силы сопротивления для него несколько больше. Отметим также, что представленные в данной работе затупленные формы оптимального тела, проникающего в мягкую грунтовую среду, качественно соответствуют результатам других авторов [10–14], рассматривавших задачи проникания оптимальных тел в среды типа металла и бетона.

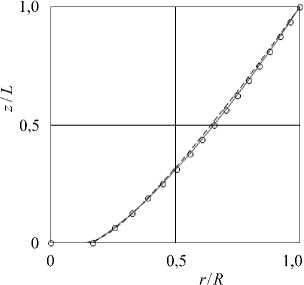
Рис. 2. Образующие оптимальных тел вращения: при кусочно-линейном представлении (маркеры о ) и в форме полинома Безье, соответствующего минимуму (2) (сплошная линия) и не соответствующего минимуму (штриховая линия)

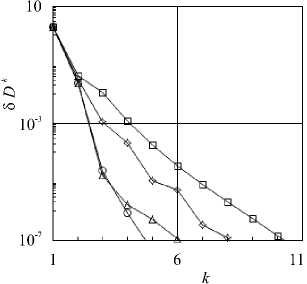
Рис. 3. Изменение величины 6 D^k на к -й итерации для различных значений 6 : 0,1 (маркеры □ ); 0,06 ( о ); 0,01 ( △ ); 0,001 ( о )

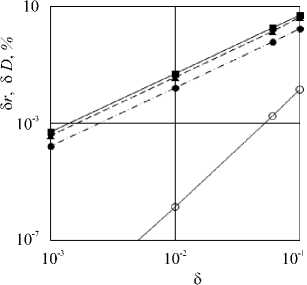
Рис. 4. Изменение относительной погрешности определения параметров образующей (темные маркеры • ▲ , ■ соответствуют i = 0,1,2 и силы сопротивления (светлые маркеры) в зависимости от величины 5

Оба численных решения установлены в результате реализации сходящегося итерационного процесса, при этом величина 6 D ^k (см. формулу (7)), убывает с ростом числа итераций к . Как показано на рисунке 3, итерационный процесс в случае приближенного вычисления производных сходится достаточно быстро. Отмечается некоторый рост скорости сходимости с уменьшением 5 от 0,1 до 0,001.

На рисунке 4 в логарифмической шкале приведены относительные погрешности определения компонент вектора параметров r образующей в форме полинома Безье 5 ri = |r * - r l/r *-100 (i = 0,1,2) и силы сопротивления 5D в зависимости от величины вариации параметров 5. В качестве величин, помеченных символом «*», принимались их численные значения, полученные при 5 = 0,0001. Видно, что безразмерная сила сопротивления имеет относительную погрешность менее 0,2% уже при 5 = 0,1; погрешность нахождения параметров полинома

является величиной порядка 1% при 5 = 0,06 .

4.    Сравнение силы сопротивления внедрению тела с вычисленной конфигурацией и абсолютно- оптимального тела

Проведем сравнение силы сопротивления внедрению оптимального тела с заданными длиной и площадью основания, обладающего сопротивлением абсолютно-оптимального конуса. Методика построения АОТ и подробный параметрический анализ приведены в работах [6-9]. Согласно [8, 9] минимум сопротивления достигается телами, имеющими постоянный угол а * между внешней нормалью к боковой поверхности и осью вращения тела, при котором функция f ( а ) в соотношениях (2)

достигает минимума на отрезке [0,1]. При постоянной скорости внедрения, как в рассматриваемой задаче, величина а* обуславливается только параметрами среды. К абсолютно-оптимальным телам вращения относится и круговой конус с заданной площадью основания.

Рассмотрим далее поведение силы сопротивления (2) в зависимости от изменения параметра модели C , характеризующего прочность среды. Известно [8, 9], что с ростом увеличение значения как а * , так и f ( a * ) . При значении C = C l и, соответственно, а * = а *

безразмерного

C происходит сопротивление

АОТ будет равняться сопротивлению конуса с заданной длиной l . Вычисленным оптимальным телом, определяемым по формулам (3)-(7), также будет конус. При C = C m ( а * = а*_т ) выполняется соотношение mn f ^(а) = f ⁽ a m ) = f ^{( 1 )} , то есть локальный и краевой экстремумы функции f ( а ) совпадают.

Абсолютно-оптимальными телами в этом случае будут: конус длиной l = lm ; цилиндр с плоским передним торцом; все промежуточные конфигурации, заключенные между произвольными поперечными сечениями конического тела и его поверхностью. Сопротивление таких тел будет составлять D = f (1). Наконец, при C > Cm АОТ станет тело с плоским передним торцом [8, 9]. При заданных выше параметрах задачи l = 55 и Cl =0,01 получено а* =0,07; рассчитанное значение а* = sinп =0,41 соотносится с Cl =0,6, предельное а*т =0,58 отвечает предельной же величине Cm =1,31.

На рисунке 6 приведены кривые силы сопротивления внедрению, отнесенной к величине f ( 1 ) , соответствующей C = C*_т , в зависимости от параметра прочности среды C/C m . Как видно из рисунка, сопротивление оптимального тела заданной безразмерной длины (удлинения) l = 5$ (штриховая кривая) больше сопротивления АОТ при 0 <  C <  C l . С увеличением параметра прочности среды происходит уменьшение радиуса переднего торца оптимального тела r₀ (см. Рис. 1, 2), и при C = C l (на рисунке 6 эта точка помечена маркером « о » ) r ₀ становится равным нулю.

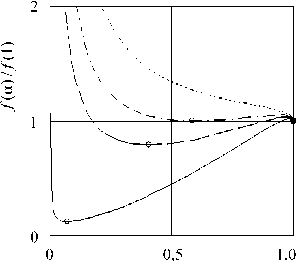
Рис. 5. Зависимости f (а)/ f ( 1 ) при различных значениях C : 0,01 (сплошная линия); C l ( l = V? ) (штриховая линия); C m (штрихпунктирная линия); 5 C m (пунктирная линия); локальные ( о ) и краевой (•) минимумы функции (2)

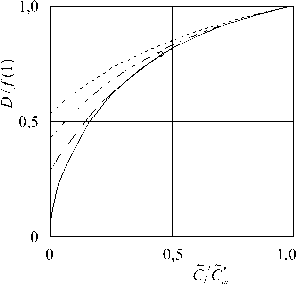
Рис. 6. Силы сопротивления внедрению Dj f ( 1 ) в зависимости от C/C m : АОТ (сплошная линия), оптимальное тело заданной длины l = V5 (штриховая линия) и l = l m (штрихпунктирная линия), круговой конус длиной l = l m (пунктирная линия); маркером « о » помечена точка C = 6_t

Наибольшее различие сил сопротивления внедрению оптимального тела с торцом и АОТ наблюдается при малых значениях C. Для АОТ, кроме того, отмечается увеличение относительной длины l, обращающейся в бесконечность при C = 0 . Для количественной оценки разницы сопротивлений введем величину 5D = (D - D*)/D* -100 , где D

сопротивление оптимального тела или кругового конуса

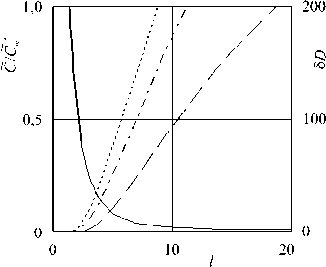
Рис. 7. Параметр прочности среды C/C*_т (сплошная линия, шкала слева) и величина 5 D (шкала справа) в зависимости от относительной длины АОТ: штриховая, штрихпунктирная и пунктирная линии отвечают 5 D оптимальных тел, соответственно, безразмерной длиной l = V5 , l_m и кругового конуса

длиной l = l m

заданной длины, D ^* — сопротивление АОТ, которые вычисляются при одинаковых значениях параметра прочности среды C .

Как видно из рисунка 7, при малых значениях характеристики прочности среды сопротивление оптимального тела заданной безразмерной длины l = 5s может превышать сопротивление АОТ на 100% при относительной длине последнего, равной 10. При C = 0,05 и заданной безразмерной длине l = Л длина АОТ составляет l = 7 и 5D ® 50 %; при длине l = 5 оптимальное тело и конус заданной длины имеют 5D, соответственно, 20% и 30%. При допустимых безразмерных длинах АОТ, изменяющимся в пределах 5s < l < 5, оптимальное затупленное тело с торцом и круговой конус заданной длины становятся близкими к абсолютно-оптимальному конусу по испытываемому при внедрении сопротивлению.

5.    Заключение

В работе показано соответствие сил сопротивления внедрению и форм оптимальных тел вращения, полученных в сходящихся численных расчетах при кусочно-линейном представлении искомой образующей и в виде квадратичного полинома Безье. Таким образом, применяемая ранее в задачах аэродинамики [28] аппроксимация является удачной параметризацией образующей тела и в случае проникания его в грунт. Изложенный алгоритм, подобно [15, 18], может быть обобщен на случай расчета силы сопротивления внедрению в постановке механики сплошных сред с использованием лагранжевых сеток с локальной автоматической перестройкой [29] или эйлеро-лагранжевых сеток [30].

Работа выполнена при финансовой поддержке Совета по грантам Президента РФ для ведущих научных школ (грант НШ-2843.2012.8) и РФФИ (проекты № 13-08-00531-а, 13-08-00658-а).