Цифровая адаптивная система для измерения частоты и амплитуды

DOI:

В ряде задач радиофизики и радиотехники измерение параметров нестационарных систем сводится к анализу квазигармонических колебаний следующего вида:

х (t) = X (t) cos (0 (t)) ,                                     (1)

то есть к определению законов изменения амплитуды X (t) и мгновенной частоты, которая является производной полной фазы: w(t) = 0(t). Большинство существующих цифровых методов не позволяет с достаточной точностью получить оценку мгновенной частоты на коротком (порядка двух периодов сигнала) интервале наблюдения, либо требует существенных вычислительных затрат.

В работах [3; 6; 7] описан цифровой параметрический метод оценивания мгновенной частоты сигнала (1), в работе [4] он дополнен методом измерения амплитуды и проведен анализ его точности и устойчивости, а в статье [5] приведены результаты сравнения его характеристик с характеристиками аналогичных методов. Метод позволяет оперативно получить достаточно точные оценки частоты узкополосных сигналов, но его погрешности существенно возрастают, если частота изменяется медленно, но достаточно сильно. Для сохранения высокой точности необходимо изменять один из параметров этого метода при изменении частоты, то есть применять адаптацию. В данной работе предлагается структура адаптивной системы для измерения частоты и амплитуды сигналов вида (1) с медленно меняющимися параметрами.

Рассмотрим три значения смеси сигнала (1) с белым нормальным шумом ^(t) с нулевым средним и дисперсией о ² в точках t — кТ, (к = 0,1, 2), где Т удовлетворяет условиям медленности изменения частоты и амплитуды [3]:

1                               1 •

XT (t) <  тХ (t), 0(t) <  Т ⁰ (t)

Более строгие условия единственности квазигармонического представления (1) приведены в работе [1]. Если параметр Т удовлетворяет условию Найквиста: Т < 1/(2f _max ), где f max — максимальная частота спектра сигнала x(t), оценки частоты и амплитуды будут иметь вид [4]:

/(«-Т ) = 2ПТ “^“s (* (‘2+(i -Т^) ) =f (i — Т) + 6/ ( — Т) ,(3)

X(t — т ) = XXТTXX!xX—T) = x (t — т) + бх (t — т).(4)

sin (2nf (t — Т ) Т}

Систематические и случайные погрешности этих оценок определяются выражениями:

X \   , ,   2         1 + 2cos2 (2nfT)

(5f) = пТctg (2п fT) f +       tg (0) ’ °f = Q 2У2Т2 • 2M ™ °

2nX              ^f     8n ² X 2 1 ² sin ² (2nf 1 ) cos ² (0)

nXT ² (cos ² (0) — cos ² (2nfT )) tg (0)

^ ) =----------- sin _(2nfT)           f — T ctg (2nf T) tg (0) X ,

σ

х

4 sin2 (0 + 2nfT) sin2 (0 — 2nfT) + sin2 (0) (sin2 (0 + 2nfT) + sin2 (0 — 2nfT))

арккосинуса в формуле (3) можно найти путем минимизации функционала погрешности:

— x[k] — x[k — 2Q] ) .

J 1 [n] =    ]E   ( 2x[k - Q] cos (2nf[n]QA^

k = n - M +1

Целочисленный параметр M = L — 2Q определяет количество усреднений в рамках скользящего окна. Подкоренное выражение в формуле (4) можно найти, усреднив его в том же диапазоне. Оценки частоты и амплитуды примут следующий вид:

^{f [ n ]} =

——— arccos 2nQA

^ E    (x[k — 2Q] + x[k])x[k — Q] ^

k = n - M +1

n

2 E    x ² [k — Q]

k = n - M +1                  /

^^^{[ n ]} =

n

∑︀ k=n-M +1

(x ² [k — Q]

— x[k]x[k — 2Q])

У М sin ( 2nf [n]QA ^

Эти оценки соответствуют моменту времени (n — R)A, где R = (L — 1)/2 - задержка оценок. Будем полагать, что L и M нечетны, тогда задержка будет содержать целое количество интервалов A. Погрешности оценок (5) и (6), вызванные наличием аддитивного шума с дисперсией о ² , получены в работе [4] для случая M ^ Q:

2Г 1                                                1                                            2

°^{[n — R ]} = 2n ² A 2 QM ² Х ² [n — R] sin ² (2nf [n — R]QA) ° ’

2 [ M — 32 — (2M — Q) cos 2 (2nf [n — R]QA) + M cos ⁴ (2nf [n — R]QA) ]

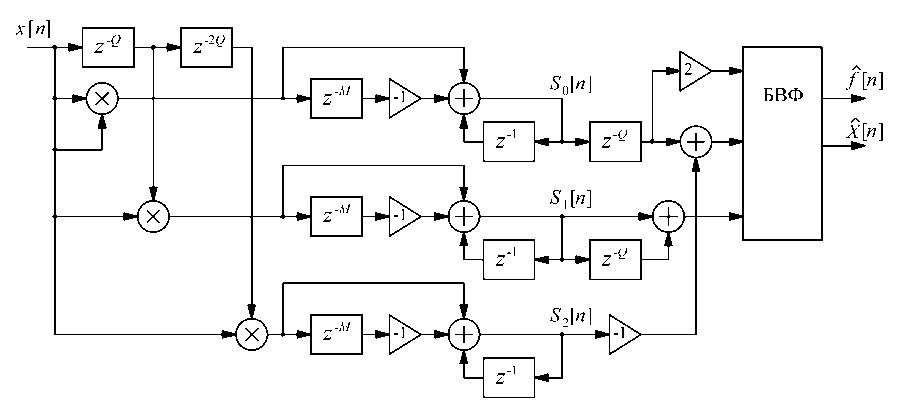
Рис. 1. Cтруктурная схема системы для оценивания частоты и амплитуды

Структура системы для оценивания частоты и амплитуды представлена на рисунке 1. Видно, что расчет трех сумм S 0 [п], S 1 [п] и S 2 [п] и их комбинаций, входящих в выражения (9) и (10), требует всего 11 операций сложения и одно умножение и легко реализуется средств а ми цифровой фильтрации. Блок вычисления функций (БВФ) arccos(x/y), sin(x) и ^х может быть реализован на базе массивов памяти, в которые заранее вводятся значения этих функций.

Если частота сигнала (1) изменяется медленно в соответствии с условием (2), но достаточно сильно, для минимизации погрешностей (7) можно корректировать коэффициент прореживания Q, не изменяя шаг дискретизации Д. При этом частота дискретизации должна существенно превышать даже максимальную частоту сигнала:

Д/ max <  1.

Построим систему из двух идентичных каналов, считая неизменной длину скользящего окна L:

L = 2Q 1 + M i = 2Q 2 + М 2

и полагая, что L ^ Q1 и L ^ Q2. При запуске этой системы первый канал является ведущим, а выходные оценки системы совпадают с его оценками: f[п] = f1 [п], X[п] = = X1 [п]. После окончания переходного процесса длительностью LД в рамках каждого окна [(к — 1)LД, (kL — 1)Д] (к > 1) рассчитывается средняя частота и оптимальное значение целочисленного коэффициента прореживания Q0, которое передается первому каналу:

ki -i

.

4/Д

f = ^ /Н ^Q0

n =( k -1) L

Ведущим становится второй канал, а выходные оценки системы принимают вид: f [п] = = f ₂ [п], ХС[п] = X 2 [п]. В первом канале начинается переходный процесс. Этот алгоритм продолжается непрерывно, а предложенная система является адаптивной.

На рисунке 2 показаны временные диаграммы, иллюстрирующие описанный процесс. Адаптивные системы активно используются при решении задач оценивания параметров сигналов [2].

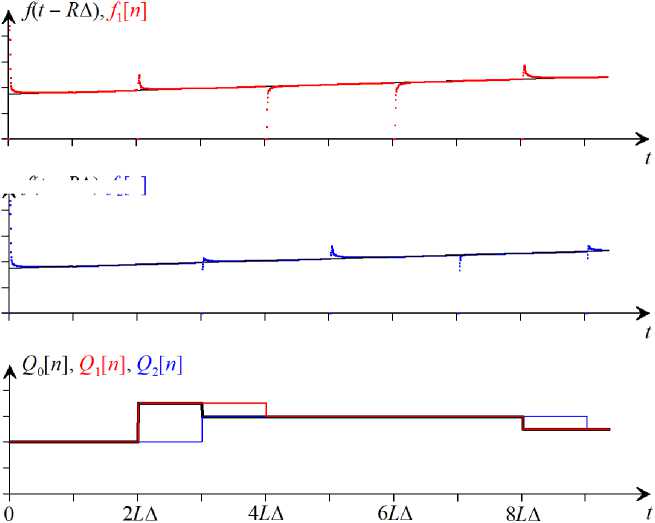
Рис. 2. Временные диаграммы работы адаптивной системы

Л>-ЛДМ;И

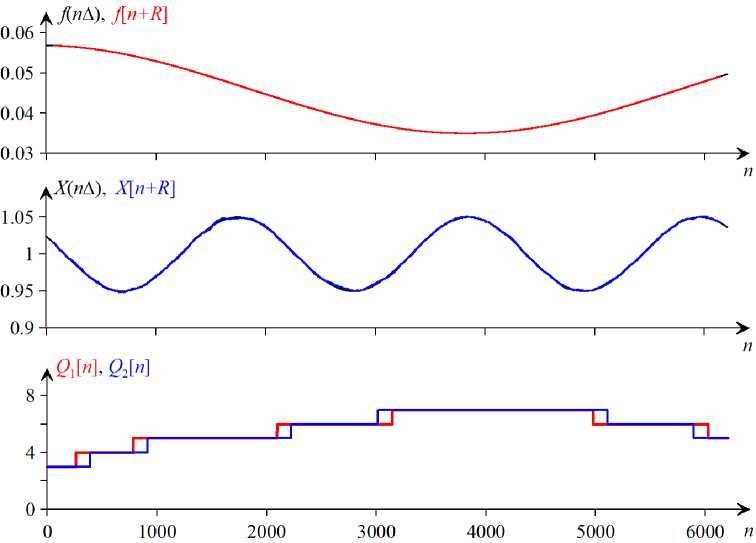
Рис. 3. Результаты обработки модельного сигнала

Для проверки работы предложенного адаптивного метода было проведено численное моделирование. Обрабатывалась последовательность отсчетов сигнала х[п] с тональной амплитудной и частотной модуляцией при наличии аддитивного шума:

х[п] = X [п] cos(0[n]) + ^[п], п = 0,... ,N — 1.

Задавались гармонические законы изменения амплитуды, частоты и полной фазы:

X [п] = Х о + А _х cos (|ПпА + ф_Х) ,  f [п] = f o + A f cos ^|ПnA + ф^ ,

0[п] = lпfonA + AfTf sin ^|ПпА + ф^ + фо, где А = 1, Хо = 1, Ах = 0,05, Тх = I105A, фх = 1,07, f0 = 0,046, Af = 0,011, Tf = 7834А, фf = 0,081, ф0 = 0,081, n = 0,01, N = 6110, длина скользящего окна L = 131. Результаты обработки представлены на рисунке 3.

Максимальные относительные отклонения оценок частоты и амплитуды в диапазоне [IL,..., N — 1] составили 5 f = 0,00091 и 5 _х = 0,0036. Для того же сигнала при том же значении L рассчитывались оценки частоты и амплитуды без адаптации с фиксированным значением Q. Максимальные отклонения оценок в зависимости от Q представлены в таблице. Видно, что адаптивный метод дает лучшие результаты, особенно, если заранее неизвестно хотя бы приближенное значение частоты.

Максимальные относительные отклонения оценок частоты и амплитуды

Q	1	2	3	4	5	6	7	8
б /	0,01361	0,00391	0,00223	0,00150	0,00102	0,00094	0,00094	0,00151
5 х	0,00854	0,00376	0,00356	0,00374	0,00364	0,00366	0,00369	0,00752

Предложенная цифровая адаптивная система для динамического измерения частоты и амплитуды квазигармонических сигналов может быть реализована на базе сигнальных процессоров, таких как ADSP-BF532, ADSP-21261, TMS320C6745, или на базе микроконтроллера с поддержкой инструкций ЦОС, например, STM32H750.