Цифровая оценка содержания питательных веществ в почве и потребность растений в удобрении при депрессии роста

Актуальность проблемы. Необходимость и актуальность разработки цифровой модели роста и продуктивности сельскохозяйственных растений (культур) определена в основных положениях Программы «Цифровая экономика Российской Федерации» [1], где отмечается целесообразность создания условий для развития общества знаний, повышения доступности и качества товаров и услуг, произведенных в цифровой экономике с использованием современных цифровых технологий. В частности, в статьях С.Б. Огнивцева [2; 3; 4] описаны этапы развития информационных технологий, как-то: автоматизация, информация, цифровизация и т. д. Рассмотрены тенденции и понятия современного этапа цифровизации и сквозные технологии, предлагаемые программой «Цифровая экономика». Обосновывается необходимость создания цифровой плат- формы АПК как важной составляющей современной цифровой экономики. Целью разработки и развития цифровой платформы АПК является увеличение эффективности работы сельскохозяйственных и агропромышленных предприятий за счет широкого внедрения в производственные процессы новых цифровых, в том числе сквозных, технологий и инновационных бизнес-моделей рыночного взаимодействия этих предприятий на основе модели «Платформа как сервис». Определяются задачи и структура цифровой платформы, в которую входят субплатформы, соответствующие агро-продовольственным рынкам, и модули-приложения, служащие для решения различных практических задач. Выделяются и описываются три основные субплатформы. Предлагается последовательность этапов разработки цифровой платформы. Обосновывается экономический эффект внедрения предлагаемой платформы и необходимость государственных вложений в этот проект [2; 3; 4].

В статьях В.И. Меденникова, Ф.И. Ереш-ко, В.В. Кульбы [5; 6] с системных позиций рассматривается процесс детермино -логизации появившихся в связи со всеобщей цифровизацией общества новых понятий: «цифровая экосистема», «экосистема цифровой экономики», «цифровая бизнес-экосистема», «цифровая платформенная экосистема» и т. д. Показано, что бизнес-сообщество в погоне за модными словами, уже не обладающими научной точностью, приводит к упрощению заключенных в них понятий, которые в результате теряют строгую концептуальность, системность, однозначность. Многозначность понятий, усиленная такой же неопределенностью трактовки цифровой платформы, представленной десятками определений, ведет к размыванию и запутыванию научного системного подхода к цифровизации управления реальной экономики, к ее дезинтеграции, то есть к огромному числу вариантов развития данного процесса, препятствующему выполнению основного требования цифровой экономики -максимальной интеграции данных и алгоритмов. Исходя из этого определения и результатов моделирования, рассматриваются методы формирования научно обоснованной цифровой экосистемы агропромышленного комплекса, основу которой составляет единое информационное интернет-пространство цифрового взаимодействия страны, интегрирующего единую цифровую платформу управления производством и единую платформу информационных научно-образовательных ресурсов. Комплексная реализация представленной цифровой экосистемы АПК позволит сократить затраты на выполнение программы цифровой экономики в десятки-сотни раз со значительно большей эффективностью [6].

В работе Н.Н. Сологуб, О.И. Улановой, Н.И. Остробородовой, Д.А. Остро-бородовой [8] подробно рассматриваются проблемы и перспективы внедрения цифровых технологий в сельское хозяйство Российской Федерации на современном этапе. Проведен анализ состояния аграрного комплекса в контексте инновационного развития. В сельском хозяйстве возрастает необходимость в применении современных технологий, в том числе систем сбора, хранения и обработки данных. Использование IT-технологий способствует повышению урожайности и рентабельности сельского хозяйства, снижению материальных затрат, более эффективному распределению средств. Обозначены основные направления цифровизации аграрного сектора, предусматривающие прохождение нескольких этапов. Выделены приоритетные задачи, реализация которых станет возможна благодаря государственной поддержке и согласованной работе всех заинтересованных участников данного процесса. В настоящее время существуют факторы, препятствующие внедрению цифровых технологий в сельское хозяйство; решению существующих проблем будет спо- собствовать разработка новой аграрной технологической политики, включающей совершенствование нормативно-правовой базы, увеличение государственной финансовой поддержки сельхозпроизводителей, внедрение новых образовательных стандартов обучения высококвалифицированных специалистов для цифрового сельского хозяйства [8].

По мнению авторов работы [8], в условиях глобализации для повышения конкурентоспособности своей продукции Россия должна принять вызовы цифровизации и активно внедрять IT-технологии в сельское хозяйство. Цифровые технологии позволяют контролировать полный цикл растениеводства или животноводства – «умные» устройства измеряют и передают параметры почвы, растений, микроклимата и т. д. Все эти данные с датчиков, дронов и другой техники анализируются специальными программами. Мобильные или онлайн-приложения приходят на помощь фермерам и агрономам, чтобы определить благоприятное время для посадки или сбора урожая, рассчитать схему удобрений, спрогнозировать урожай и многое другое. Внедрение передовых информационных технологий сократит объем ручного труда и расходы, повысив при этом производительность и урожайность [8].

В целом в проанализированных статьях [2; 3; 4; 5; 6; 7; 8] рассмотрены концептуальные вопросы работы цифровой экономики в АПК, поэтому важно разработать математические (цифровые) модели для конкретных процессов и сельскохозяйственных технологий.

В ранее опубликованных статьях [9; 10] получено обобщение математической модели академика Э.А. Митчерлиха [11; 12; 13] для « закона действия факторов роста » без учета депрессии роста растений; чтобы исключить повторения, ниже в таблице 1 приведены показатели сравнительного анализа цифровых моделей роста и продуктивности по работам [11; 12; 13].

Таблица 1

Сравнительный анализ моделей роста и продуктивности растений

№ п/п	Митчерлих Э.А.		Григулецкий В.Г.
1	Основное уравнение
	dy = k ( A - У ) dx		f 1- ) d- = c ( А - У ) ^ B + у ) dx
2	Начальные условия
	У ( x 0	= У 0	У ( x 0	= У 0
3	Частное решение
	1g '            ' lg И А - У ) _	= к ( x - x 0 )	ln Г ( A - У 0 X B + У ) L ( А - у )( B + у 0 ) _	= c ( А + B )( x - x 0 )
4	Максимальный урожай
	A = У 2 - У 1 ■ У 3 2 У 2 - У 1 - У 3		A + B = 2 У 0 + У і )( У 0 + У 2 )( У 0 + У з ) - ( У 0 + У 2 1 2 ( У 1 У з + 2 У 0 1 ( У 0 + У і )( У 0 + У з ) - ( У 0 + У з ) 2
5	Коэффициент действия фактора
	lg ( A - У 1	- lg ( A - У 2 )	c  М( A - у 0 )( B + у ) ] - lnK B + у 0 )( A - у )]
	x 2 - x		( А + B )( x - x 0 )
6	Количество питательных веществ в почве
	b = lg ( A ) - lg ( A - У 0 ■ k		b = ln [ A ( B + У 0 )] - ln [ B ( A - У 0 )] ( А + B ) c

Из таблицы 1 видно, что предложенная в работах [9; 10] цифровая модель роста и продуктивности растений является более общей, чем известная модель академика Э.А. Митчерлиха [11; 12; 13].

Основные положения методики Э.А. Митчерлиха по определению потребности почвы в удобрении. Чтобы исключить разночтения, воспользуемся содержанием работ [11; 12; 13] более детально. Во введении книги [13] ее автор, академик Э.А. Митчерлих специально формулирует проблему химического анализа почвы в почвоведении в виде следующего вопроса: задача сводится к определению питательных веществ, имеющихся в почве в доступной для растений форме; естественно, важно определить, что именно извлекает растение из почвы и какое количество питательных веществ находится в урожае, это главные вопросы химического анализа почв; однако количество питательных веществ, извлекаемых на одной и той же почве разными растениями зависит от влажности почвы, температуры окружающей среды, состава почвы и т. д. Химический анализ почвы должен проводиться с учетом физиологии растения химико- физическими методами для конкретных условий. Определяя практические рекомендации по оценке потребности почвы в удобрении, академик Э.А. Митчерлих [12; 13] использует следующее основное положение: урожай (у) возрастает с увеличением фактора роста (х) пропорционально количеству урожая, недостающего до наивысшего (А), возможного при избытке данного фактора, поэтому можно записать основное уравнение:

dy = ⁽ A ^- y ) c       (1)

dx

(уравнение (1), стр. 510, [11]; уравнение (1), стр. 21, [13]), где с – коэффициент пропорциональности.

Дифференциальное уравнение первого порядка в обыкновенных производных (1) определяет абсолютную скорость изменения урожая ( у ) от действия какого-либо фактора роста ( х ). Общий интеграл дифференциального уравнения (1) можно записать в виде:

lg ( A - y ) = С - ex      (2)

(соотношение (2), стр. 510, [11]; соотношение (2), стр. 22, [13]), где С – постоянная интегрирования.

В книге [13] специально отмечается, что при полном отсутствии питательных веществ (т. е. когда х = 0, урожай у = 0) , можно записать соотношения:

lg ( A - 0 ) = С - с • 0

или:

log A = С, и получить частное решение основного уравнения:

lg ( A - y ) = log A - ex (3)

(соотношение (3), стр. 22, [13]), где с – коэффициент действия какого-либо питательного вещества почвы или удобрения, а произведение (cx) пропорционально повышению урожая, и если 28

при ( х ) некоторого питательного вещества получается урожай ( у ), то ( х ) тем больше, чем меньше коэффициент ( с ), и, наоборот, поэтому можно записать частное решение основного дифференциального уравнения (1) в виде:

y = A ( 1 - e - cx )         (4)

(соотношение (4), стр. 22, [13]).

В случае, когда почва еще до внесения в нее удобрения сама по себе обеспечивает некоторый урожай растений ( а ), то можно принять:

х = 0, у = а и найти соотношения:

lg ( A - a ) = С - e • 0

или:

C = lg(A - a), или:

lg ( A - y ) = lg ( A - a ) - ex (5)

(соотношение (7), стр. 24, [13]), где а – урожай, который обусловлен тем, что в самой почве, еще до внесения в нее данного питательного вещества (х), находилось некоторое его количество (x = b), и можно записать соотношение:

log ( A - a ) = log ( A ) - eb     (6)

и найти формулу:

log ( A - y ) = log ( A ) - e ( x + b ) (7)

(соотношение (9), стр. 24 [13]).

Таким образом, увеличивая одно из питательных веществ (х) и оставляя все остальные факторы постоянными, опытным путем можем определить количество данного питательного вещества (b) в почве, используя данные об урожайности для конкретного растения и почвы: пусть с неудобренной почвы получен некоторый урожай (у0), соответствующий запасу (b) некоторого питательного веще- ства, и поэтому можно записать соотношения:

'log (A - y0 ) = log (A)- cb, tog (A - y) = log (A) - с(x + b), из которых следует:

log ( A - y 0 ) - log ( A - y ) = ex ,   (8)

или:

A = y 0 ^- ky 1 - k

( k = e ^cx )

(соотношение (10), стр. 25, [13]), и найти соотношение:

_b = lg ⁽ A ^{) -} lg ⁽ A ^- y 0 ) c

(формула (10), стр. 25, [13]), которое определяет запас питательных веществ в почве, используя данные об урожайности для конкретных природных условий и определенных сельскохозяйственных растений.

Главным недостатком методики Э.А. Митчерлиха [12; 13; 14] является то обстоятельство, что основное дифференциальное уравнение (1), его частное решение (4) и основная формула (10), определяющая запас питательных веществ в почве, получены на основе предположения, что кривая роста у(х) и убывания рентабельности последовательных доз удобрений всюду выпукла. Профессор В. Н. Перегудов в критической статье [15] специально отмечает, что постоянная выпуклость кривой роста не наблюдалась в 30 % результатов (563 опыта) полевых опытов; в 171 опыте наблюдалась обратная зависимость – кривая роста имела вогнутый характер, а чаще всего – 40 % результатов – опытные кривые роста имеют сначала вогнутый участок, а затем выпуклый участок, при- ближаясь к некоторому максимальному значению.

Новая цифровая модель оценки запаса питательных веществ в почве. Принимаем справедливость следующего утверждения: урожайность (у) и ее прибавка возрастают при увеличении количества фактора роста (х) и пропорциональны количеству урожая (А – у), не достигшего максимального предельного значения (А) и возможному значению урожая (В + у, выше некоторого минимального (начального) значения (В) урожая, и поэтому можно записать основное уравнение:

f ^ 1 dy = ( A - y ) k ’      (11)

^ B + y ) dx где k – коэффициент пропорциональности, или:

dy = k ( A - y )( B + y ) .         ⁽¹²⁾

dx

Сравнивая уравнения (1) (Э.А. Мит- черлих), (11) и (12), можно отметить, что используемое дифференциальное уравнение первого порядка в обыкновенных производных (11) определяет относительную скорость изменения урожая (у) от действия какого-либо фактора роста (х). Общий интеграл дифференциального уравнения (11) можно записать в виде:

ln ( A - y ) - ln ( B + y ) = C - k ( A + B ) x ,  (13)

где C – постоянная интегрирования; с = k ( A + B) – коэффициент действия какого-либо питательного вещества почвы или удобрения.

При полном отсутствии питательных веществ в почве ( х = 0), можно принять у = 0 и записать соотношение:

ln ( A ) - ln ( B ) = C                  (14)

и получить « частное решение » уравнения (11) в виде:

1 I     A I , 1 I B + У I

In I------I + In ----— = cx.

( A - y )   ( B )

Для решения основного дифференциального уравнения (11) можно назначить «начальные» условия:

У (xo ) = У о,

где х 0 , y 0 – постоянные параметры, определяющие соответственно «начальное» значение фактора роста ( x 0 ) и «начальное» значение урожая ( y 0 ).

Решение основного дифференциального уравнения (11), удовлетворяющее начальным условиям (16), можно записать в виде:

л.) ₌ A ⁽ B ⁺ У о ^{) e}xP[ k ⁽ A ⁺ B ⁾⁽ x ^- x о ^{)] -} B ⁽ A - У о ) . ⁽¹⁷⁾

⁽ B ⁺ У о ^{) ex}P [ k ⁽ A ⁺ B ⁾⁽ x ^- x о ^{)] + (} A - У о )

Значение коэффициента (А) можно найти по формуле:

Д ₊ g _ 2 ^{( У} 1 ⁺ B X ^У 2 ⁺ B X ^У 3 ⁺ B ^{) - ( У} 2 ⁺ B ^{) 2 ( У} 1 ^{+ У} 3 ^{+ 2} B ) , ⁽¹⁸⁾

^{( У} 1 ⁺ B )( ^У 3 ⁺ B ^{) - ( У} 2 ⁺ B ^{) 2}

где y 1 , y 2 , y 3 – экспериментальные (опытные) значения урожая, установленные через равные интервалы изменения фактора роста ( х ), т. е. х 3 – х 2 = х 2 – х 1 и соответственно y 1 = y ( х 1 ), y 2 = y ( х 2 ), y 3 = y ( х 3 ).

Если с неудобренной почвы получен некоторый урожай ( у ну ), соответствующий некоторому запасу питательных веществ ( х = х ну ), то из формулы (15) можно получить соотношение:

ln ⁽ A ^)- ln| A ^- У ну| + ln| B + У ну| ^- ln ⁽ B )   (19)

xну = b = или:

x ну = b =

11 . (20)

Формулы (19) (или (20) определяют запас питательных веществ в почве. Сравнивая соотношения (1) (Э.А. Митчерлих) и (11) (предлагаемая), (2) (Э.А. Митчер-лих) и (12) (предлагаемая), (3) (Э.А. Мит-30

черлих) и (15) (предлагаемая), (4) (Э.А. Митчерлих) и (17) (предлагаемая), можно отметить, что в методике Э.А. Митчерлиха не учитывается возможное значение урожая (В + у) выше некоторого минимального (начального) значения (В). По существу в методике Митчерлиха не учитывается влияние малого количества (или отсутствие) питательных веществ (удобрений) на величину урожая растения. Можно отметить, что формула (17) определяет кривую роста урожайности, у которой, в частном случае, имеются выпуклый и вогнутый участки в отличие от формулы (4) (Э.А. Митчерлих), которая всюду выпукла, что часто не подтверждается в экспериментах      (опытах).      Значение коэффициента действия фактора роста (k) при этом необходимо определять по формуле для каждого интервала:

, _ In ^[( A ^- У о ⁾⁽ B + У , j ] In ^[( B + У о ⁾⁽ A ^- У , ) I. (21) k i =              ( A + B )( x , - x , - 1 )

Применение новой методики оценки запаса питательных веществ в почве. Пример 1. Рассмотрим опытные данные о влиянии фосфорных удобрений ( х ) на урожайность овса ( у ), полученные в опытах Э.А. Митчерлиха и представленные в таблице II (табл. II, стр. 541, [11]); именно относительно этих данных в статье [11] из условия у = 0 из уравнения lg(94,6 – y ) = 1,9613 – 0,258 x    по    методике

Э.А. Митчерлиха получена потребность питательных веществ без удобрения ( х = b ) при урожае у ну = 3,1 г на сосуд: b = 0,056 г ([11], стр. 541) (табл. 2).

Таблица 2

Урожайность овса (у) в зависимости от количества фосфорных удобрений (х) в опытах Э.А. Митчерлиха (табл. II, стр. 541, [11])

Показатель	№ п/п
	1	2	3	4	5
Доза удобрения, г	0,00	0,10	0,25	0,50	1,00
Урожай (опыт), г	3,1	8,40	15,8	26,6	44,1
Урожай (расчет), г (Э. А. Митчерлих)	–	8,4	15,0	25,0	44,1

Отметим, что для опытных данных из таблицы 2 в статье [11] получено уравнение:

lg(94,6 – y ) = 1,9613 – 0,258 x.

Расчетные значения урожая овса ( у ) при разных дозах фосфора ( х ) приведены в четвертой строке таблицы 2, и специально отмечается, что для у = 0 получено значение b = х = 0,056 г, которое определяет потребность питательных веществ в опытном сосуде.

Воспользуемся новой методикой расчета; из данных таблицы 2 используем значения:

у ( х 0 ) = 3,1; у ( х 1 ) = 8,40; у ( х 2 ) = 15,8; у ( х 3 ) = 26,6; у ( х 4 ) = 44,1;

х 0 = 0,0; х 1 = 0,10; х 2 = 0,25; х 3 = 0,50; х 4 = 1,00.

Таблица 3

Урожайность яровой ржи (у) в зависимости от азотных удобрений (х) в опытах

Леммермана (табл. 5, стр. 77, [16])

Показатель	№ п/п
	1	2	3	4	5
Доза удобрения, ц/га	0,00	0,20	0,40	0,60	0,80
Урожай (опыт), ц/га	32,7	39,8	45,4	51,7	52,6
Урожай (расчет), Митчерлих	–	39,1	45,2	50,9	56,3
Урожай (расчет), Леммерман	–	39,7	45,4	49,8	53,3

По формуле (18) находим максимально возможное значение урожая ( А ):

_{А + в}_ 2 ( 8,4 + 8,4 )( 8,4 + 26,6 )( 8,4 + 44,1 ) - ( 8,4 + 26,6 ) ² ( 8,4 + 44,1 + 16,8 -,

~                ( 8,4 + 8,4 )( 8,4 + 44,1 ) - ( 8,4 + 26,6 ) 2

или:

А + 8,4 = 67,5; А = у max = 59,1 г.

По формуле (21) определяем коэффициент действия фактора ( с 1 ) на интервале изменения от х 1 = 0,00 г до х 2 = 0,10 г, где у ( х 1 ) = 3,1 г и у ( х 2 ) = 8,4 г:

^с 1 =

ln [( 59,1 - 3,1 )( 8,4 + 8,4 )] - ln [( 8,4 + 3,1 )( 59,1 - 8,4 )] ( 59,1 + 8,4 )( 0,10 - 0,00 )

= 0,070883 ,

и находим значение k 1 :

k 1 = c 1 ( A + B ) = 0,070883 (59,1 + 8,4) = 4,784576.

По формуле (19) (или (20) находим потребность питательных веществ ( х ну ) в почве в одном сосуде для условий опытов Э.А. Митчерлиха [11]:

x ну

4,784576

ln

59,1    )

59,1 - 3,1 J

+ һ

8,4 + 3,1

8,4

= 0,0769 г .

Пример 2. Рассмотрим опытные данные Леммермана о влиянии азота ( х ) на урожайность ( у ) яровой ржи; эти результаты приведены в книге А.Т. Кирсанова ([16], стр. 77, табл. 5 (табл. 3).

Для опытных данных Э. А. Митчерлих получил уравнение:

lg(150 – y ) = 2,0693 – 0,122 x.

Расчетные значения урожая ржи ( у ) при разных значениях азота ( х ) по этому уравнению приведены в четвертой строке таблицы 3. Леммерман для опытных данных получил уравнение:

lg(67 – y ) = 1,5350 – 0,5 x.

Расчетные значения урожая ржи ( у ) при разных значениях азота ( х ) по этому уравнению приведены в последней (пятой) строке таблицы 3; оба уравнения определили расчетные значения урожая ржи с высокой точностью относительно экспериментальных данных. Но можно отметить значительное различие максимального урожая А = 150 ц/га (Митчер-лих) и А = 67 ц/га (Леммерман), также значительно различаются «коэффициенты действия факторов роста» с = 0,122 (Мит-черлих) и с = 0,500 (Леммерман), что свидетельствует о необходимости уточнения и дальнейшго развития теории Э.А. Митчерлиха .

Воспользуемся следующими данными из таблицы 3:

у 0 = 32,7; у ( х 1 ) = 39,8; у ( х 2 ) = 45,4; у ( х 3 ) = 51,7; у ( х 4 ) = 52,6;

х 0 = 0,0;   х 1 = 0,20;   х 2 = 0,40;   х 3 = 0,60;

х 4 = 0,80.

По формуле (18) находим максимально возможное значение урожая ( А ):

_{д + в =} 2 ( 45,4 + 39,8 )( 51,7 + 39,8 )( 52,6 + 39,8 ) - ( 51,7 + 39,8 ) 2 ( 45,4 + 52,6 + 79,6 )

"                  ( 45,4 + 39,8 )( 52,6 + 39,8 ) - ( 51,7 + 39,8 ) 2                   ^,

или:

А + 39,8 = 92,54 ц/га; А = у max = 52,74 ц/га.

По формуле (21) определяем коэффициент действия фактора роста (с1) на интервале изменения от х1 = 0,00 до х2 = 0,20, где    у(х1) = 32,7 ц/га и у(х2) = 39,8 ц/га:

ln [ ( 52,74 - 32,7 )( 39,8+39,8 ) ] -ln [ ( 39,8+32,7 )( 52,74 - 39,8 ) ]

с =----------------7-----------77----------7----------------= 0,028681

1                    (52,74 + 39,8)(0,20 - 0,00)                     , и находим значение k1:

k 1 = c 1 ( A + B ) = 0,028681 (52,74 + 39,8) = 2,654171.

По формуле (19) (или (20) находим потребность питательных веществ ( х ну ) в почве для условий экспериментов Лем-мермана:

x _ну

2,654171

f    52,74     ) , f 39,8 + 32,7'

ln lI + ln l

( 52,74 - 32,7 J (    39,8

= 1,0509 ц I га .

Если использовать методику Э.А. Мит-черлиха, то по формуле (10) можно найти значение:

b = lgN5.4 lg ^{( 150 -} 32.7 ) = 0     . 0 ц / _га ,

0,122

т. е. на 16,8 % меньше, чем по новой методике.

Пример 3. Рассмотрим опытные результаты изучения агротехники возделывания новых сортов риса при реакции на землях Краснодарского края [17]. Опыты проведены в 2019 г. на полях учхоза «Кубань», норма высева семян составляла 7,0 и 3,5 млн шт/га, ширина междурядий была 15,0 и 30,0 см, глубина заделки семян – 1,0–2,0 см и 4,0–6,0 см. Посев проводили сеялкой СН-16 по одному проходу каждого сорта, где нарезали 15 равных частей, на общем фоне предпосевного внесения карбамида (N 92 ) дополнительно вносили карбамид вручную через каждые 12 дней после посева, таким образом, получили семь вариантов и контрольный вариант (без подкормки). В опытах установлены оптимальные сроки подкормки 32

для пяти сортов риса (Ежик, Ивушка М., Ивушка Б., Светлана, Хазар), часть опытных данных приведена (табл. 5, стр. 176, [17]) (табл. 4).

Таблица 4

Урожайность сортов риса при оптимальных сроках подкормки, ц/га

Показатель	Вариант					Сорт риса
	1	2	3	4	5
Доза, ц/га	0	38	43	46	55	–
Урожай, ц/га	98,9	120,9	121,4	121,5	121,5	Ежик

Из данных таблицы 4 используем следующие результаты:

у 0 = 98,9; у ( х 1 ) = 120,9; у ( х 2 ) = 121,4; у ( х 3 ) = 121,5; у ( х 4 ) = 121,5;

х 0 = 0,0; х 1 = 38; х 2 = 43; х 3 = 46;

х 4 = 55;

А = у max = 121,5 ц/га; B = у min = 120,9 ц/га.

По формуле (21) определяем коэффициент действия фактора роста ( k 1 ) на интервале изменения от х 0 = 0,00, где у 0 (0) = 98,9 ц/га до х 1 = 38,00 ц/га и у 1 (38) = 120,9 ц/га:

k = In [(121,5 - 98,9)(120,9 + 120,9)]- In [(120,9 + 98,9)(121,5 -120,9)] = Q 00053() 1                           (121,5 + 120,9)(38 - 0)                            , и находим значение (с1):

с 1 = k 1 ( A + B ) = 0,128471.

По формуле (19) (или (20) находим потребность питательных веществ в почве ( х ну ) для условий опытов авторов работы [17]:

^x ну

0,128471

f 121,5    )  , f 120,9 + 98,9 )'

lnl----------’-------| + lnl-----’---------— I

( 121,5 - 98,9 J    (    120,9 J

= 17,75 ц I га .

Пример 4. Воспользуемся результатами опытов Э.А. Митчерлиха, в которых изучалось определение содержания питательных веществ в почве и потребность почвы в удобрении ([14], стр. 221–234). В опытах использовалось девять сосудов, которые наполнялись равным количеством одинаковой почвенно-песчаной смеси; к этой смеси в качестве общего фона добавляли 1,5 г сухой углекислой и 1,2 г раствора азота в форме нитрата аммония, 1,0 г кристаллического сульфата магния, 0,5 г хлористого натрия. Результаты опытов приведены в таблице 5 (табл. 76, стр. 223, [14]).

Результаты опытов и вычислений на почвенно-песчаной смеси для урожайности картофеля

Количество К 2 О, г	Почва: песок = = 0 : 5		Почва: песок = = 1 : 4		Почва: песок = = 2 : 3		Почва: песок = = 3 : 2		Почва : песок = = 4 : 1
	найде но	вы-числено	найде но	вы- чис ле но	найде но	вы-числе но	найде но	вы-числено	най дено	вы- чис ле но
0,00	6,4 ± 2,9	10,8	55,0 ± 1,7	55,1	66,7 ± 1,3	68,8	70,6 ± 0,5	72,5	73,0 ± 2,5	74,6
0,10	29,1 ± 2,0	28,0	56,4 ± 4,7	59,9	68,7 ± 0,2	70,2	73,1 ± 1,3	72,9	74,6 ± 1,1	74,7
0,25	44,7 ± 2,4	45,7	64,6 ± 0,7	64,7	69,9 ± 0,8	71,6	74,2 ± 0,5	73,3	75,3 ± 0,8	74,8
0,50	62,7 ± 1,0	61,9	68,3 ± 0,8	69,2	73,6 ± 0,5	72,9	75,6 ± 0,6	73,7	76,0 ± 1,4	74,9
1,00	70,2 ± 2,6	73,0	73,6 ± 2,0	72,2	75,7 ± 1,7	73,8	77,1 ± 0,6	73,9	78,7 ± 1,8	75,0
А		76,0		73,0		74,0		74,0		75,0

В таблицах 6–10 приведены результаты опытов и вычислений на почвенно -песчаной смеси разного состава для урожайности картофеля по новой методике.

Таблица 6

Результаты опытов и вычислений урожайности картофеля на почвенно-песчаной смеси (почва : песок = 0: 5; А = 70,39;

В = 6,4) по новой методике (3столбец) и методике Э.А. Митчерлиха (4 столбец)

Таблица 7

Результаты опытов и вычислений урожайности картофеля на почвенно-песчаной смеси (почва : песок = 1: 4; А = 76,52;

В = 55,0) по новой методике (3 столбец) и методике Э.А. Митчерлиха (4 столбец)

Таблица 5

№ п/п	Опыт ( х і )	Опыт ( У і )	Расчет ( У і )	Расчет ( У і )	Расчет ( сі )
	номер столбца
	1	2	3	4	5
1	0,00	55,0	55,00	55,1	—
2	0,10	56,4	56,40	59,9	0,0061
3	0,25	64,6	58,36	64,7	0,0030
4	0,50	68,3	71,86	69,2	0,0122
5	1,00	73,0	72,71	72,2	0,0164

По формуле (19) (или (20) находим запас питательных веществ ( х ну ) в почве по данным таблицы 7:

1          Г, 5    76,52    )   ( 5 55 + 55 )!   ~    ~  ,

:  = у-------х--------- lnI ----------- I + lnI -------- I = 2,4452 г / сосуд.

^ну    ( 131,52 ) - 0,0061 L ( 76,52 - 55 J (   55 JJ

Таблица 8

Результаты опытов и вычислений урожайности картофеля на почвенно-песчаной смеси (почва : песок = 2 : 3; А = 76,56;

В = 66,7) по новой методике (3 столбец) и методике Э.А. Митчерлиха (4 столбец)

№ п/п.	Опыт ( Х і )	Опыт ( У , )	Расчет ( У)	Расчет ( У)	Расчет ( С)
	номер столбца
	1	2	3	4	5
1	0,00	66,7	66,7	68,8	—
2	0,10	68,7	68,7	70,2	0,0169
3	0,25	69,9	70,99	71,6	0,0081
4	0,50	73,6	71,52	72,9	0,0234
5	1,00	75,7	75,99	73,8	0,0175

По формуле (19) (или (20) находим запас питательных веществ ( х ну ) в почве по данным таблицы 8:

№ п/п	Опыт ( х і )	Опыт (У і )	Расчет (У і )	Расчет (У і )	Расчет ( с і )
	номер столбца
	1	2	3	4	5
1	0,00	6,4	6,40	10,8	—
2	0,10	29,1	29,10	28,0	0,1899
3	0,25	44,7	61,52	45,7	0,0728
4	0,50	62,7	61,90	61,9	0,0785
5	1,00	70,2	69,97	73,0	0,0991

^x ну

( 143,26 ) - 0,0169

ln I

76,56

76,56 - 66,7

( 66,7 + 66,7 )|                  .

+ ln I -------- I I = 1,1328 г / сосуд.

Таблица 9

По формуле (19) (или (20) находим запас питательных веществ ( х ну ) в почве по данным таблицы 6:

Результаты опытов и вычислений урожайности картофеля на почвенно-песчаной смеси (почва : песок = 3 : 2; А = 77,71;

В = 70,6) по новой методике (3 столбец) и методике Э.А. Митчерлиха (4столбец)

X.... =  ----------;-------------- ну   (76,79)-0,1899

Г, (   70,39   )  .(6,4 + 6,4JJ            , ln I-------------I + ln I-----------I = 0,0541 г / сосуд.

L 1 70,39 - 6,4 J (    6,4 JJ

№ п/п	Опыт ( х )	Опыт ( У . )	Расчет ( У - )	Расчет ( У і )	Расчет ( с )
	номер столбца
	1	2	3	4	5
1	0,00	70,6	70,60	72,5	—
2	0,10	73,1	73,10	72,9	0,0304
3	0,25	74,2	75,33	73,3	0,0126
4	0,50	75,6	75,49	73,7	0,0140
5	1,00	77,1	76,96	73,9	0,0169

По формуле (19) (или (20) находим запас питательных веществ ( х ну ) в почве по данным таблицы 9:

ну

( 148,31 ) - 0,0304

Г, (    77,71    )  , ( 70,6 + 70,6ҮІ

In I---------------------- I + ln II

L ( 77,71 - 70,6 J    (    70,6 JJ

= 0,6842 г / сосуд.

Таблица 10

Результаты опытов и вычислений урожайности картофеля на почвенно-песчаной смеси (почва : песок = 4 : 1; А = 98,86; В = 73,0) по новой методике (3 столбец) и методике Э.А. Митчерлиха (4 столбец)

№ п/п	Опыт ( х i )	Опыт ( y i )	Расчет ( y i )	Расчет ( y i )	Расчет ( с i )
	номер столбца
	1	2	3	4	5
1	0,00	73,0	73,00	74,6	–
2	0,10	74,6	74,60	74,7	0,0044
3	0,25	75,3	76,81	74,8	0,0013
4	0,50	76,0	76,43	74,9	0,0008
5	1,00	78,7	77,35	75,0	0,0017

По формуле (19) (или (20) находим запас питательных веществ ( х ну ) в почве по данным таблицы 10:

^x ну

(171,86) - 0,044

ln I

98,86    ) , ( 73,0 + 73,0 YI

----------------------- I + ln I --------------------- I

98,86 - 73,0 J (    73,0    JJ

= 0,2690 г / сосуд.

Из данных таблиц 6–10 (столбцы 3, 4) видно, что во всех вариантах результаты расчетов по новой методике значительно ближе к опытным значениям, чем результаты вычислений по методике Э.А. Мит-черлиха.

Цифровая оценка потребности растений в удобрении при депрессии роста. « Закон действия факторов роста » имеет вполне определенные пределы применения: при использовании большого количества какого-нибудь фактора роста (например, высокие дозы растворимых удобрений) урожай уменьшается; при большом количестве питательных веществ в почве нельзя получить высокий урожай, т. к. происходят повреждения стеблей и листьев растений из-за большой концентрации питательного вещества (раствора) в почве, а в концентрированном растворе солей не может расти ни одно растение.

Академик Э.А. Митчерлих совместно с профессором Б. Бауле при обработке опытных данных установили, что каждый из действующих факторов роста, влияющих на рост и развитие растения, имеет оптимальное значение, за которым следует угнетение роста и урожайности, т. е. происходит депрессия развития растения, поэтому в основное уравнение была введена « поправка на депрессию » [14; 16]. Поправка на депрессию определяет « второе приближение » закона действия факторов роста Митчерлиха.

В книге А.Т. Кирсанова ([16], стр. 69) специально отмечается, что « несмотря на всю стройность, изящность и убедительность этих выводов с математической стороны », все же их нельзя признать достаточными для наших целей без предварительной проверки в наших опытах. Анализ полученных опытных данных свидетельствует о необходимости уточнения и развития основных положений этой теории. Сущность депрессии развития растений академик Э.А. Мит-черлих показывает на процессе роста овса при недостатках калийных удобрений и высоких дозах других удобрений. «Второе приближение» особенно ценно для тех вариантов, когда используются «односторонние» удобрения, например, применяются калийные удобрения на фоне разных доз азотистых удобрений. В качестве примера в таблице 11 приведен фактический урожай общей массы зерна и соломы при разных количествах азота (г/сосуд) в опытах Э.А. Митчерлиха.

Первое приближение закона действия факторов роста для данных таблицы 1 определено по формуле:

у_г ( x ) = 158,5 [ 1 - 10 ^- 0,3^{96 (} x ^{+ 0},^{025 )} ] .

Второе приближение определялось по формуле:

y₂ ( x ) = 158,5 [ 1 - 10 - °'^{396 (} x ^{+ 0}.^{025 )} ] - 10 - ° ⁰»i x +M2⁵ ) ’

Можно, однако, отметить, что данные столбцов 3 и 4 в таблице 11 различаются значительно, что свидетельствует о необходимости уточнения теоретической части «второго приближения» закона действия факторов роста.

y ( x ) = a [ 1 - 10 " cx ]        (23)

(соотношение (15), стр. 72, [16]).

Соотношения (22) и (23) являются точными частными решениями опубликованного дифференциального уравнения первого порядка:

Таблица 11

Общий урожай овса в зависимости от доз азотных удобрений

Количество азота на сосуд в г	Общий урожай в граммах
	полученный Виссманом урожай	вычисленный урожай по 2-му приближению	вычисленный урожай по 1-му приближению
0,000	6,8 ± 0,38	3,5	3,5
0,125	18,6 ± 0,45	20,3	20,3
0,250	32,6 ± 1,05	35,1	35,1
0,375	46,5 ± 1,01	48,4	48,4
0,50	58,1 ± 0,65	59,9	60,3
0,75	80,3 ± 1,25	79,1	80,3
1,00	95,8 ± 2,03	93,8	96,2
1,50	116,2 ± 2,96	112,3	119,0
2,0	118,2 ± 3,91	120,3	135,5
3,0	116,1 ± 3,02	117,7	148,5
4,0	108,4 ± 4,3	102,5	154,5
6,0	71,2 ± 4,92	63,1	157,8
8,0	18,2 ± 6,77	31,1	158,,4
10,0	5,6 ± 5,63	12,5	158,5

dy = ^c i ⁽ A ^- У ) .           ⁽²⁴⁾

dx

Для относительного повышения урожая можно записать уравнение:

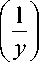
dy =f A - y I dx ^ y )

(уравнение (16), стр. 72, [16]), и специально (B. Baule) отмечается: подставляя в это уравнение соответствующие величины А – у и у согласно соотношениям (22) и (23), получим уравнение:

В книге [16] приведено детальное изложение теории B. Baule ^*) (Б. Бауле) относительного « второго приближения закона действия факторов роста ». По мнению профессора А.Т. Кирсанова, первое приближение закона Э.А. Мит-черлиха охватывало наиболее распространенные почвенные разности, характерные для Восточной Пруссии; совершенно другая ситуация возникает, если при опытах в сосудах вносят дозы удобрений, в 10 раз превосходящие значения, используемые на практике; часто такие варианты возникают и на практике, когда применяют удобрения в больших дозах. Рассмотрим основное уравнение « закона действия факторов роста » в виде:

lg ( A - У ) = lg ( A ) — ex , ⁽²²⁾ или:

f 1) dy = f1-( y ) dx \1 -10 — ^cx

)

(уравнение (17), стр. 72, [16]), и специально отмечается следующее допущение: пусть депрессия возрастает пропорционально количеству данного фактора х и равна 2kx, в этом случае можно записать уравнение:

1 ) dy f 10 — ^cx

— I— = c, I------- y ) dx \ 1 - 10 - cx

- 2 kx

(уравнение (18), стр. 73, [16]).

Интегрируя уравнение (27) можно найти соотношение:

lg ⁽ y ^{) =} lg ^{( 1 - 10} cx ^)- kx ² + c ,   ⁽²⁸⁾

или:

y ( x ) = ( 1 - 10 ^{- cx} ) • 10 ^{- kx 2} • 10 ^c     (29)

(уравнение (20), стр. 73, [16]).

Приняв значение постоянной А равным:

10 c = A ,              (30)

можно записать конечное выражение для второго приближения закона действия факторов роста:

y ( x ) = A ( 1 - 10 - cx ) - 10 - ^kx 2     (31)

(соотношение (21), стр. 73, [16]), и специально отмечается следующее: в соотношении (31) имеется два постоянных коэффициента с и k; коэффициент с академик Э.А. Митчерлих считает постоянной величиной для всех растений и условий среды, а константа k принимается постоянной только в пределах данного опыта; она изменяет свою величину в зависимости от типа растения, удобрения, вида почв, климата и т. д.; на величину k сильное влияние оказывает буферность почв: на песчаных почвах значение константы k значительно больше, чем на глинистых или почвах богатых органическими веществами и т. д.

Можно отметить следующее: уравнения:

dy = C1(A - У), dx f 1) dy    fA - y)

I I— = cI        I - 2kx ('

V y J dx V

– это два совершенно разных уравнения. Соотношение:

y (x ) = a[1 -10-c1 x ]

является точным частным решением уравнения (32) при нулевых начальных условиях. Соотношение:

y ( x ) = a ( 1 - 10 - c ¹ x ) - 10 " ^kx 2 (35)

не является частным решением уравнения (33). Это выражение вообще не явля- ется решением уравнения (33), поэтому результаты Б. Бауле–Э.А. Митчерлиха относительно «второго приближения закона действия факторов роста» нуждаются в уточнении и дальнейшем развитии. Подставляя (35) и производную первого порядка от соотношения (35) в уравнение (33), получим следующее выражение:

c 1 -10 - ^{kx 2} ln10 = ( 1 -10 - ^cx ) [ 2 kx ( ln10 +1 ) + c ln10 ] ,  ⁽³⁶⁾

которое не является тождеством и, следовательно, все результаты относительно второго приближения закона действия факторов роста являются ошибочными .

Новая  приближенная цифровая модель депрессии роста и развития растений. Принимаем справедливость утверждения: урожайность (у) и ее прибавка возрастают при увеличении количества факторов роста (х) пропорционально количеству урожая (А – у), не достигшего предельной потенциальной урожайности (А) и возможному значению урожая (В + у) выше некоторого минимального (начального) значения (В) урожая, и поэтому можно записать уравнение:

f -^1— 1 dy = ^{c (} A ^- У )(1 ^{+ 2} kx ) ,    ⁽³⁷⁾

V B + y J dx где с – коэффициент пропорциональности, называемый «коэффициентом действия фактора роста; k – коэффициент депрессии роста и развития растения; А – постоянный параметр, определяемый по экспериментальным (опытным) данным и равный «потенциальной урожайности» растения; В – постоянный параметр, определяемый по экспериментальным данным и равный «начальному» значению урожая определенной культуры для конкретной почвы, гидрометеоусловий района и ландшафта.

Для решения дифференциального уравнения (37) назначим « начальные » условия:

у ( х о ) = у 0 ,               (38)

где х о , у о - постоянные параметры, определяющие соответственно «начальное» значение фактора роста ( х о ) и «начальное» значение урожая ( у о ), можно принять у о = В.

Решение основного дифференциального уравнения (37), удовлетворяющее начальным условиям (38), можно записать в виде:

ln [( A ^- У 0 X ^{B +} У )] =^hK ^{B +} У 0 X A ^- У ) ^{] +} c ( A ^{+ B} ) [ ( x ^- x ) ⁺ k ( x 2 ^- x ^] ,⁽³⁹⁾

или в виде:

In ⁽ A + y ⁰ II ^{B +} y ^{) = c (} A ^{+ B )[(} x - x 0 ^{) +} k ⁽ x ² - x^{2 )]}

_ ( ^{B +} y 0 ⁾⁽ A y ) _

Значение коэффициента действия фактора роста ( c i ) можно находить на каждом интервале от х = х / -і до х = х / по формуле:

c = ln [ ⁽ A ^- y - i ⁾⁽ b ⁺ у - ^{)] -} lnK B ⁺ у - )( A ^- y - ^)] ,  ⁽⁴¹⁾

*         ⁽ A ^{+ B )[(} x ^- x - 1 ) ^{+ k (} x , ^{2 -} x , - ^{) ]}

где / - индекс, целое положительное число   ( / = 1, 2, 3, „.).

При таких условиях урожайность ( у / ) можно находить по формуле:

. (42)

У , '( x ) =

A ( ^{B +} У , - 1 ^{) ex} P [ c ⁽ A ^{+ B} ) [ ( x ^- x , - 1 ) ⁺ k ( Х ² - x, 2 - 1 )]] - ^B ( A ^- У - 1 ) ^{( B +} У , - 1 ^{) ex} P c ⁽ A ^{+ B )[(} x - x - 1 ) ⁺ k ⁽ x ² - x ²- i )]] + ⁽ A - У , - i )

Значение потенциальной урожайности

• ( А ) при этом определяется по формуле:

A _{+ B} = ^{2 ( B +} У 1 )( ^{B +} У 2 )( ^{B +} У 3 ^{)-( B +} У 2 ^{) 2 (} У 1 ⁺ У 3 ^{+ 2 B} ) .  ⁽⁴³⁾

^{( B + У} 1 )( ^{B + У} 3 ^{)-( B + У} 2 ^{) 2}

Соотношение (40) можно записать в виде:

• ¹   ) _Ь Г ( A - y 0 ^{)( B +} y )

. A + B J ln L ( B + У о )( A - У о ),

= a + mx + nx ,

где a = - cx о(1 + kx о);  m = c; n = ck,

• a , m , n - коэффициенты, определяемые методом наименьших квадратов.

«О птимальное » значение фактора роста ( х кр ) можно найти из уравнения:

m + 2 nx кр = О,             (45)

или:

m xкр = -^ . 2n

Чтобы уменьшить объем вычислительной работы и повысить точность расчетов, вместо основного уравнения (37), начальных условий (38) и решения в виде соотношения (40) можно используя безразмерные единицы и ( и ):

и = У , и = x,(47)

AA использовать соответственно соотношения:

du = cAB(1 + виХ1 - и), dи и (ио) = и о,  A = e B,(49)

^Һ fҒ+R u І    ^U ' J= CA^{B ( 1 + в)[(и}"^и 0 ^{) +} k ^(u 2 "^U 0 ^)]

( 1 + в и 0 JI 1 - и J

Формулы (45) и (46) остаются справедливыми.

Примеры расчетов. Пример 5. Рассмотрим влияние объема воды на урожай ячменя в опытах Гелльригеля, подробно описанные в монографии Э.Дж. Рэсселя [18]. Опытами установлено, что большой объем воды (60-8О % от объема полного насыщения песчаной почвы) приводит к уменьшению количества сухого вещества в зерне ячменя) (табл. 12).

Таблица 12

Зависимость урожая ячменя от объема снабжения водой (Рэссель Э.Дж., [18], стр. 49)

№ п/п	Опыт х / (%)	Опыт x (б. е.)	Опыт у / (г/сосуд)	Опыт У (б. е.)	Расчет У- (б. е.)
1	2	3	4	5	6
1	10	0,1	0,72	—	—
2	20	0,2	7,75	0,254415	0,217648
3	30	0,3	9,73	0,359067	0,349539
4	40	0,4	10,51	0,463706	0,432176
5	60	0,6	9,96	0,380263	0,449687
6	80	0,8	8,77	0,298281	0,270180

Ячмень выращивался в специальных сосудах с песчаной почвой, все необходимые питательные вещества в опытах обеспечивались полностью, за исключением соли (Ca(NO 3 ) 2 ), количество которой строго контролировалось по азоту (мг), а значение урожая измерялось с точностью до 1 • 10 ^-3 г [18].

Из данных таблицы 12 используем значения: у 0 = 0,72; у 1 = 7,75; у 2 = 9,73; у 3 = 10,51; В = 0,72; по формуле (43) найдем максимально возможное (потенциальную урожайность) количество сухого вещества ( А ) в зерне ячменя:

_{л + 0 72 =} 2 ( 0,72 + 7,75 )( 0,72 + 9,73 )( 0,72 + 10,51 ) - ( 10,45 ) 2 ( 19,7 ■ ,

,            ( 0,72 + 7,75 )( 0,72 + 10,51 ) - ( 0,72 + 9,73 ) 2

или:

А + 0,72 = 11,959; А = 10,876; А + В = 11,959.

Методом наименьших квадратов получим для опытных данных в безразмерных единицах (б. е.) следующую зависимость:

y ( x ) = - 0,193898 + 2,550275 x - 2,462721 x .

По формуле (46) находим максимально возможный объем воды для полива ячменя:

найдем максимально возможную массу сухого вещества ( А ) в соломе ячменя:

_{А +} j _{8 =} 2 ( 1,8 + 5,5Қ1,8 + 9,64 )( 1,8 + 11,00 ) - ( 11,44 ) ² ( 20,1 ) _{= 13} ^

’                        (7,3)(12,8)-(11,44)2                          ’    ’ или:

Таблица 13

Зависимость количества сухого вещества в соломе ячменя (г) от объема воды при поливе (Рэссель Э.Дж., [18], стр. 49)

Показатель	№ п/п
	1	2	3	4	5	6
Количество воды*, б. е.	0,10	0,20	0,30	0,40	0,60	0,80
Масса сухого вещества, г	1,80	5,50	8,20	9,64	11,00	9,47
* 1,00 (или 100 %) означает количество воды, требуемой для полного насыщения песчаной почвы в сосудах

А = 11,361; В = 1,8; А + В = 13,161.

Методом наименьших квадратов получим для опытных данных в безразмерных единицах (б. е.) следующую зависимость:

y ( x ) =- 0,157581 + 1,524067 x - 1,297166 x ².

По формуле (46) находим максимально возможный объем воды для полива ячменя:

^x кр

^2,550275 = 0,518 ,

2 • 2,462721

x кр

2,52426г = 0,5 87, 2 • 1,297166

или:

или:

хкр = 51,8 %, что подтверждается экспериментальными данными (хкр * 52 %) (табл. 12).

Профессор Э.Дж. Рэссель [18] поясняет это тем, что « излишек воды сокращает приток воздуха к корням ».

Пример 6. Рассмотрим опытные данные о количестве сухого вещества в соломе ячменя в зависимости от объема воды при поливе, подробно описанные в монографии Э.Дж. Рэссель [18], таблица 13.

Из данных таблицы 13 используем значения: у 0 = 1,8; у 1 = 5,5; у 2 = 9,64; у 3 = 11,00; В = 1,8, по формуле (43)

хкр = 58,7 %, что подтверждается экспериментальными данными, таблица 13 (хкр « 60 %).

Пример 7 . Рассмотрим результаты лабораторных опытов Э.А. Митчерлиха, полученные при изучении влияния азотистых удобрений на урожай овса (табл. 12); по опытным данным установлено значение потенциальной урожайности овса ( А = 158,5 г/сосуд); методом наименьших квадратов [19] для опытных данных таблицы 12 получено уравнение:

u ( x ) = –0,00055 х ² + 0,00442 х + 0,004217.

Оптимальное количество азота на сосуд (по формуле (46) равно:

^x кр

^0,00442 _ 4 02 г/сосуд,

2 • 0,00055    , что подтверждается экспериментальными данными.

Значение х кр = 4,02 г/сосуд является критическим, оно определяет количество азота, превышение которого (в виде азотных удобрений) будет способствовать уменьшению урожайности овса.