Цифровая оценка влияния удобрений на урожайность сельскохозяйственных растений

Введение. В работах Э.А. Митчерлиха [1; 2; 3] показано эффективное применение « закона совокупного действия факторов роста » для оценки действия на урожайность разных сельскохозяйственных растений; в монографии [4], в частности, приведены результаты полевых и вегетационных опытов применения фосфорной кислоты (§ 52, С. 267–273, [4]), действия калийных удобрений на урожай растений (§ 53, С. 273–281, [4]) и т. д.

Изменение прироста урожая ( dy ) с повышением фактора роста ( dx ) в «законе совокупного действия факторов роста» описывается уравнением:

dy = C 1 ( A - y ) (1)

dx

(уравнение (1), стр. 21, [2]; уравнение (1), стр. 243, [4]), где y – величина урожая;

х – фактор роста;

A – наивысший урожай;

с 1 – коэффициент действия фактора роста ( должен быть величиной постоянной , стр. 25, [2]).

На основе большого количества опытов в сосудах (более 3000 опытов) по методике Э.А. Митчерлиха определены следующие значения разных удобрений для азота, калия и фосфорной кислоты: азот, с = 0,122; калий без натрия, с = 0,33;

калий с натрием, с = 0,93; фосфорная кислота, с = 0,60 (стр. 29, [2]).

Решение уравнения (1) принимается в виде:

lg ( A - y ) = 1g A - ex          (2)

(соотношение (7), стр. 25, [2]; формула (5), стр. 215, [4]), или:

y = A [1-10-cx ]                (3)

(соотношение (6), стр. 215, [4]).

В монографии [4] отмечается, что при значении с = 0,301 и х = 1 всегда достигается половина высшего урожая ([4], стр. 215). По мнению профессора А.Т. Кирсанова [5], «нет другого более ценного метода для определения потребности почвы в удобрениях, чем методика Э.А. Митчерлиха» [1; 2; 3]. В Бюллетене Отдела земледелия Государственного института опытной агрономии ([5], стр. 149–150) отмечается, что при рассмотрении 54 случаев удобрений овса в 51 опыте получили совпадение теоретического урожая с фактическим, на ячмене из 48 случаев полное согласие результатов получено для 45 опытов. В большинстве результаты лабораторных опытов в сосудах соответствовали данным полевых опытов; наименьшее согласование результатов получено на бедных почвах. Проверяя основные положения теории Митчерлиха на опытах в сосудах для овса, А.Т. Кирсанов отмечает следующее: для этой проверки необходимо установить фактические запасы питательных веществ, эквивалентных вносимому удобрению; трудности установления запасов состоят в недостаточно точной обоснованности выбора коэффициентов для перехода от запасов питательных веществ в сосуде к запасам в самой почве. Мит-черлих берет в качестве такого множителя число «2», а для азота он устанавливает широкие пределы этого множителя – от значения 0,5 до значения 4,0, в зависимости от гигроскопичности почвы и ее механического состава; для почв бедных, песчанистых используется низкий коэффициент, для почв глинистых принимается высокое значение; неопределенность коэффициентов перехода от опытов в сосудах к результатам полевых опытов для реальной почвы определяет необходимость уточнения и развития теории Э.А. Митчерлиха [1; 2; 3; 4]. В ранее опубликованных нами работах [6; 7; 8] получено обобщение «закона совокупного действия фактора роста» путем учета особенностей роста и развития растений при низких (малых) урожаях (продуктивности).

Новая цифровая модель роста и урожайности сельскохозяйственных растений. Принимаем справедливость следующего утверждения: урожайность (у) и ее прибавка возрастают при увеличении количества фактора роста (х) пропорционально количеству урожая (А – у), не достигшего до максимального предельного значения (А), и возможному значению урожая (В + у), выше некоторого минимального значения (В) урожая, и поэтому можно записать основное уравнение:

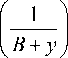
dy dx

( A - У ) k ,

где k – коэффициент пропорциональности, который можно назвать « относительным коэффициентом действия фактора роста ».

При разделении переменных [9] можно записать для неопределенного интеграла:

f 7-----dy-----\ = kfdx.

J(B + yIA-y)J

Можно найти соотношение:

1=f ■         ■■

( B + y )( A - y ) I A + B Д B + y ¹ t A - У )

и вычислить интеграл (5) в виде:

h|B+y| - h|A - y| = k(A+B)x + C, где С – постоянная интегрирования, определяемая по начальным условиям:

y(x0) = y0,(8)

где х 0 , у 0 – постоянные значения, определяющие начальное количество фактора роста ( х 0 ) и соответствующий урожай ( у 0 ).

Частное решение уравнения (4), удовлетворяющее начальным условиям (8), можно записать в виде:

ln

B + y b + у о

- In

A - У

^{A - y} 0

= k ( A + B )( x - x 0 ) ,    (9)

или:

₌ ^{A ( B +} У о ^{) e}xp [ ^{k ( A + B )( x - x} о ^{)] - B ( A -} У о )    (10)

^{( B +} У 0 ^{) e}xp [ ^{k ( A + B} X ^{x - x} 0 )] + ( ^{A -} У 0 )

Коэффициент действия фактора роста ( с ) можно найти из соотношения (9) в виде:

c = k ( A ₊ B ) = ^h[( A - y о X ^{B +} y ) ^]~ ^{h[( B +} y оX A - y ) ^] . (11) X - x 0

Значение максимального урожая ( А ) можно найти по фактическим опытным данным или из соотношения:

l j]₌ ^{2 ( У} 1 ^{+ B} )( ^У 2 ^{+ B} )( ^У 3 ^{+ B )-( У} 2 ^{+ B} X ^{( У} 1 ^{+ У} 3 ^{+ 2 B} )       (12)

(У1 + B \ У 3 + B)-(У 2 + B)2            , где y1, y2, y3 – экспериментальные (опытные) значения урожая (у), установленные через равные интервалы изменения фактора роста (х), т. е. х3 – х2 = х2 – х1 и соответственно y1 = y(х1), y2 = y(х2), y3 = y(х3).

В практических расчетах целесообразно определять значение коэффициента действия фактора роста ( с ) на интервале изменения фактора роста ( х ) от значения х = x i , где у = у i = у ( x i ) до значения х = x i +1 , где у = у i +1 = у ( x i +1 ):

c = c = k (A+в ) = ln[(A - y-i)(B+y)]- ln[(B+y-i)(A - y)]

i                                              x,- xi-i, и величину урожая соответственно:

y = y = A(B + y,-i )exp[c(xi- x-i)]- B(A - y,-i)

^{i     (} B ⁺ y - i ^{) e}xp ^[ c i ( x ^- x i - 1 ^)]+( A ^- y , - i ) .

Если планируется (прогнозируется) получить урожай ( у ) в количестве ( у = у пр ), то необходимое значение удобрения ( х ) или фактора роста ( х = х пр ) можно определить по формуле:

Пример 1. Влияние азота на урожай. Рассмотрим результаты вегетационных опытов Е. Вольфа-Хоэнхейма (E. Wolf-Hohenheim), описанные в монографии Э.А. Митчерлиха ([4], стр. 265, табл. 106) (табл.) 1.

X™ = xn +       \ пр 0  k (A + B)

к B+y Л (A— у h II-h II

I B ^{+ y} 0 J I A ^- y 0 J

Количество питательных веществ в почве ( х 0 ) при значении урожая ( у = у 0 ) можно определить по формуле:

i I’d A W B I

=                ln I            |- ln |            I

⁰   k ( A + B ) [ ^ A - y ₀ J   ^ B + y ₀ 1

или:

k ( A + B )

, ( A I .I B + y ₀1 ln I------------I + In II

I A ^{- y} 0 J I B J

Соотношения (13)–(17) являются основными, которые можно использовать при внедрении «цифровых» технологий и выполнении подпрограммы «Цифровое земледелие» [10; 11; 12; 13; 14] в отраслевой программе «Цифровое сельское хозяйство» [15; 16].

Применение новой цифровой методики оценки влияния разных удобрений на урожайность сельскохозяйственных растений

По формуле (12) находим значение максимального урожая ( А ) по данным:

у1 = у(0,156) = 17,43; у2 = у(0,208) = 19,78; у3 = у(0,260) = 21,19, для которых выполняется условие:

х 3 – х 2 = х 2 – х 1 , или: 0,260 – 0,208 = 0,208 – 0,156,

2 ( 3,36 + 17,43 )( 3,36 + 19,78 )( 3,36 + 21,19 ) - ( 23,14 ) 2 ( 45,34 )

⁺ ’                           ( 20,79 )( 24,55 ) - ( 23,14 ) ²

или:

A + 3,36 = 26,028; А = 22,668; В = 3,36.

По формуле (13) находим коэффициент действия ( с = с 1 ) на интервале от х = х 0 = 0,000, где у 0 = 3,36, до значения х = х 1 = 0,052, где у 1 = 9,31:

ln [(22,668 - 3,36)(3,36 + 9,31)] - ln [(3,36 + 3,36)(22,668 - 9,31)] c1 =----------------------0(052-0(000----------------------, или:

с 1 = 19,279.

Таблица 1

Результаты опытов Е. Вольфа-Хоэнхейма по влиянию азота на урожай водных культур

№ п/п	Доза азота ( х i ), г	Урожай, опыт ( у i ), г	Урожай, расчет ( у i ), г	Коэффициент действия ( c i )	Урожай, расчет ( ȳ i ), г
1	0,000	3,36	3,360	–	3,36
2	0,052	9,31	9,310	19,279	9,37
3	0,104	13,99	15,407	14,340	13,86
4	0,156	17,43	17,676	13,187	17,20
5	0,208	19,78	19,736	13,509	19,69
6	0,260	21,19	21,152	14,020	21,55

По формуле (14) находим формулу для урожая:

x ₀

19,279

(   22,668   ) . (3,36 + 3,36 j hl-------------1 + lnl —-------— I

( 22,668 - 3,36 J    (    3,36    J

= 0,044 г .

, x 22,668 ( 3,36 + 3,36 ) exp [ 19,279 ( x ) ] - 3,36 ( 22,668 - 3,36 )

y ¹ x =          ( 3,36 + 3,36 ) exp [ 19,279 ( x ) ] + 19,308         ’

По формуле (15) определим количество азотного удобрения ( х = х пр ) для получения, например, урожая у = у пр = 15,0 г:

и соответственно значения:

87,454

P ( 0 )^_------- = 3,360 ,

¹       26,028

^x пр

= 0,044 +

19,279

( 3,36 +15 )  , ( 22,668 -15 j lnl--------------------I - lnl-------------------------I

( 3,36 + 3,36 J    ( 22,668 - 3,36 J

= 0,144 г .

P '°°5’ '   350,238 = 9’3‘° ’

37,621

прогнозное значение урожая для х = 0,104 равно:

У 1 ( 0,104 ) = 1066’352 = 15,407,

69,212

и т. д.

Расчетные (прогнозные) количества урожая ( у i ) и значения коэффициента действия факторов роста ( c i ) приведены в таблице 1 (в последнем столбце таблицы даны значения урожая (ȳ i ) по методике Э.А. Митчерлиха [4]). Данные таблицы показывают хорошее соответствие опытных и расчетных (прогнозных) значений урожая водных культур по новой методике расчета (из шести опытных значений четыре совпали с опытными данными, а по методике Э.А. Митчерлиха получено только два совпадения). Вычисленные значения по методике Э.А. Митчерлиха определены по уравнению:

lg (27 – y ) = lg (27 – 3,36) – 2,45 x .

Среднее значение коэффициента действия ( с ) по новой цифровой модели равно c̄ = 19,279, а по методике Э.А. Митчерлиха с = 2,45, т. е. в 8 раз меньше.

По формуле (17) определим запас питательных веществ в почве ( х = х 0 ) для опытных данных (контроль), когда не использовали удобрения, а получили урожай у 0 = 3,36 г:

Таким образом, запас азотных питательных веществ в почве равен х 0 = 0,044 г, и для получения урожая у пр = 15,0 г необходимо всего использовать х пр = 0,144 г азота, т. е. для значения фактора роста ( х ) можно найти: х = 0,144 – 0,044, или х = 0,100 г, и для урожая у (0,100) по формуле (14) получить:

/     x _ 22,668 ( 3,36 + 3,36 ) exp ( 19,279 - 0,100 ) - 3,36 - 19,308

y ’    =      (3,36 + 3,36)exp(19,279- 0,100) +19,308      ’ или:

y ( 0,100 ) =

^982,396 = 14,997 « 15,0 г , 65,508

как и прогнозировалось.

Пример 2. Влияние азота на урожай картофеля. Рассмотрим результаты полевых опытов А. Бидербека (A. Biederbeck), описанные в монографии Э.А. Митчер-лиха ([4], стр. 266, табл. 107) (табл. 2).

Таблица 2

Результаты опытов А. Бидербека по влиянию азота на урожай картофеля

№ п/п	Доза азота ( х i ), ц/га	Урожай, опыт ( у i ), ц/га	Урожай, расчет ( у i ), ц/га	Коэффициент действия ( c i )	Урожай, расчет ( ȳ i ), ц/га
1	0,00	210	210,00	–	210
2	0,40	246	246,00	1,089	246
3	0,60	263	260,05	1,299	262
4	0,80	277	276,99	1,299	276

По формуле (12) находим значение максимального урожая ( А ) по данным:

у1 = у(0,40) = 246; у2 = у(0,60) = 263; у3 = у(0,80) = 277, для которых выполняется условие: х3 – х2 = х2 – х1, или: 0,8 – 0,6 = 0,6 – 0,4,

2 ( 210 + 246 )( 210 + 263 )( 210 + 277 ) - ( 473 ) ² ( 943 )

⁺    ~              ( 456 )( 487 ) - ( 473 ) ²

или:

A + 210 = 540,938; А = 330,938; В = 210.

По формуле (13) находим коэффициент действия ( с = с 1 ) на интервале от х = х 0 = 0,00, где у 0 = 210, до значения х = х 1 = 0,40, где у 1 = 246:

ln[(330,938 - 210)(210 + 246)] - ln[(210 + 210)(330,938 - 246)] c1 =-----------------й-000-----------------’ или:

с 1 = 1,089.

ствия факторов роста ( c i ) показаны в таблице 2 (в последнем столбце таблицы приведены значения урожая (ȳ i ) по методике Э.А. Митчерлиха [4]). Вычисленные значения по методике Э.А. Митчерлиха определены по уравнению:

lg (425 – y ) = lg (425) – 0,20( x + 1,48).

Среднее значение коэффициента действия ( с ) по новой цифровой модели равно c̄ = 1,229, а по методике

Э.А. Митчерлиха с = 0,20, т. е. в 6 раз меньше.

По формуле (17) определим запас питательных веществ в почве ( х = х 0 ) для опытных данных (контроль), когда не использовали удобрения, а получили урожай у 0 = 210 ц/га:

x ₀

1 1,089

)    330,938    )

ln l----------------------------I

^ 330,938 - 210 )

+ ln

210 + 210 \

210 J

= 1,561 ц / га .

По формуле (14) находим формулу для урожая:

По формуле (15) определим количество азотного удобрения ( х = х пр ) для получения урожая у = у пр = 250 ц/га:

/ х_ 330,938 ( 210 + 210 ) exp [ 1,089 ( х )] -210 ( 330,938-210 )

y ^{1 Х} =          ( 210 + 210 ) exp [ 1,089 ( х )] + 120,938         ,

^x пр

= 1,561 + —

^,        1,089

1 210 + 250 3 J330,938 - 250 \ ln |I - ln |I

) 210 + 210 J ) 330,938 - 210 J

= 2,013 ц / га .

и соответственно значения:

113596,98

у ( 0,00 ) =----------= 210,00,

¹           540,938

у ( 0,40 ) = ^189472,4366 = 246,00,

1  ,         770,212          ,   , прогнозное значение урожая для х = 0,60 равно:

у ( 0,60 ) = ^241758,4113 = 260,05,

¹           928,205

и т. д.

Расчетный (прогнозный) урожай картофеля ( у i ) и значения коэффициента дей-

Таким образом, запас азотных питательных веществ в почве равен х 0 = 1,561 ц/га, и для получения урожая у пр = 250 ц/га необходимо всего использовать х пр = 2,013 ц/га азота, т. е. для значения фактора роста ( х ) можно найти: х = 2,013 – 1,561, или х = 0,452 ц/га, и для урожая у (0,452) по формуле (14) получить:

,     . _ 330,938 ( 210 + 210 ) exp ( 1,089 - 0,452 ) - 210 - ( 330,938 - 210 )

y ’   ^=          (210+210)exp(1,089-0,452)+120,938          ’ или:

201991,172

у ( 0,452 ) =----------- = 249,977 « 250 ц / га ,

808,040

как и прогнозировалось.

Пример 3. Влияние фосфора на урожай. Рассмотрим результаты 3045 опытов Герике, описанные в монографии Э.А. Митчерлиха ([4], стр. 272, табл. 112) по применению фосфорной кислоты на урожай зерновых (табл. 3).

^x пр

= 1,638 + —

^,        1,221

. ( 22,8 + 27 V . ( 31,265 - 27 V lnl---------------I- ln|------------------I

^ 22,8 + 22,8 J ^ 31,265 - 22,8 J

= 2,272

ц / га .

Таблица 3

Результаты опытов Герике по влиянию фосфора на урожай зерновых (3045 опытов)

№ п/п	Доза Р 2 О 5 ( х i ), ц/га	Урожай, опыт ( у i ), ц/га	Урожай, расчет ( у i ), ц/га	Коэффициент действия ( c i )	Урожай, расчет ( ȳ i ), ц/га
1	0,00	22,8	22,80	–	22,8
2	0,30	25,1	25,10	1,221	25,1
3	0,60	26,1	26,83	0,659	26,5
4	0,90	27,8	26,95	1,445	27,9
5	1,20	28,2	28,97	0,435	28,2

Таким образом, запас фосфорных питательных веществ в почве равен х 0 = 1,638 ц/га, и для получения урожая у пр = 27,0 ц/га необходимо всего использовать х пр = 2,272 ц/га фосфора, т. е. для значения фактора роста ( х ) можно найти: х = 2,272 – 1,638, или х = 0,634 ц/га, и для урожая у (0,634) по формуле (14) получить:

/ a _ 31,265 ( 22,8 + 22,8 ) exp ( 1,221 ■ 0,634 ) - 22,8 ■ 8,465 y ^,      =       ( 22,8 + 22,8 ) exp ( 1,221 - 0,634 ) + 8,465       ^,

или:

По формуле (12) находим значение максимального урожая: А = 31,265 ц/га ( В = 22,8 ц/га). По формуле (13) находим значения коэффициентов действия ( с i ) на разных интервалах изменения дозы удобрений (0,00–0,30), (0,30–0,60), (0,60–0,90), (0,90–1,20) и соответствующие количества урожая по формуле (14); результаты расчетов приведены в таблице 3, где в последнем столбце даны значения урожая зерновых по методике Э.А. Митчерлиха, которые определены по уравнению:

lg (29,4 – y ) = lg (29,4) – 0,6( x + 1,09).

Среднее значение коэффициента действия ( с ) по новой цифровой модели равно c̄ = 0,940, а по методике Э.А. Митчерлиха с = 0,60, т. е. в 1,6 раз меньше.

По формуле (17) определим запас питательных веществ в почве ( х = х 0 ) для опытных данных (контроль), когда не использовали удобрения, а получили урожай у 0 = 22,8 ц/га:

У ( 0,634 ) =

2898,825

107,356

= 27,001 ц / га ,

как и прогнозировалось.

Пример 4. Влияние фосфора на урожай. Рассмотрим результаты 1642 опытов Герике, описанные в монографии Э.А. Митчерлиха ([4], стр. 272, табл. 112) по применению фосфорной кислоты на урожай картофеля (табл. 4).

Таблица 4

Результаты опытов Герике по влиянию фосфора на урожай картофеля (1642 опыта)

№ п/п	Доза Р 2 О 5 ( х i ), ц/га	Урожай, опыт ( у i ), ц/га	Урожай, расчет ( у i ), ц/га	Коэффициент действия ( c i )	Урожай, расчет ( ȳ i ), ц/га
1	0,00	237	237,00	–	237
2	0,30	251	251,00	1,066	253
3	0,60	261	261,69	0,987	263
4	0,90	269	268,71	1,031	270
5	1,20	275	275,04	1,023	274

x

1,221

\ ( 31,265   ^ ,2 22,8 + 22,8V ln|-------,---------I + ln| —,---------- I

^ 31,265 - 22,8 J    ^    22,8 J

= 1,638

ц / га .

По формуле (15) определим количество фосфорного удобрения ( х пр ) для получения, например, урожая у = у пр = 27,0 ц/га:

По формуле (12) находим значение максимального    урожая картофеля:

А = 292,476 ц/га ( В = 237 ц/га). По формуле (13) находим значения коэффициентов действия ( с i ) на разных интервалах изменения дозы фосфорных удобрений (0,00– 0,30), (0,30–0,60), (0,60–0,90), (0,90–1,20) и соответствующие расчетные количества 89

урожая картофеля по формуле (14); результаты расчетов приведены в таблице 4, где в последнем столбце приведены значения урожая картофеля по методике Э.А. Митчерлиха, которые определены по уравнению:

lg (283 – y ) = lg (283) – 0,6( x + 1,34).

Среднее значение коэффициента действия фактора роста ( с ) для фосфорных удобрений по новой цифровой модели равно c̄ = 1,027, а по методике Э.А. Митчерлиха с = 0,60, т. е. в 1,7 раз меньше.

По формуле (17) определим запас питательных веществ в почве ( х = х 0 ) для опытных данных (контроль), когда не использовали удобрения, а получили урожай у 0 = 237 ц/га:

x

1 1,066

\ (   292,476   \ , ( 237 + 237 4

Inl-------------------1 + In ------------- t292,476 - 237 J   (   237   )

= 2,210 ц / га .

По формуле (15) определим количество фосфорного удобрения ( х пр ) для получения, например, урожая у = у пр = 255 ц/га:

x^ = 2,210 + — пр ,       1,066

\ ( 237 + 255 4 J292,476 - 255 4

ln l--------------I- ln l-------------------I

1 237 + 237 )   ( 292,476 - 237 )

= 2,613 ц / га .

Таким образом, запас фосфорных питательных веществ в почве равен х 0 = 2,210 ц/га, и для получения урожая у = у пр = 255 ц/га необходимо всего использовать х пр = 2,613 ц/га фосфора, т. е. для значения фактора роста ( х ) можно найти: х = 2,613 – 2,210, или х = 0,403 ц/га, и для урожая у (0,403) по формуле (14) получить:

/     x _ 292,476 ( 237 + 237 ) exp ( 1,066 - 0,403 ) - 237 - 55,476

y ,     =       (237 + 237)exp(1,066 - 0,403) + 55,476       , или:

199882,055

y ( 0,403 ) =----------= 255,002 ц / га ,

783,843

как и прогнозировалось.

Пример 5. Влияние калия на урожай. Рассмотрим результаты вегетационных опытов Э.А. Митчерлиха, описанные в монографии [4] (стр. 274, табл. 115) по применению калийных удобрений на урожай красного клевера (табл. 5).

Таблица 5

Результаты опытов Э.А. Митчерлиха по влиянию калия на урожай красного клевера

№ п/п	Доза К 2 О ( х i ), г	Урожай, опыт ( у i ), г	Урожай, расчет ( у i ), г	Коэффициент действия ( c i )	Урожай, расчет ( ȳ i ), г
1	0,00	32,8	32,80	–	32,8
2	0,10	37,1	37,10	1,753	37,1
3	0,25	52,7	43,10	5,079	51,6
4	0,60	56,5	69,27	0,702	62,4
5	1,50	66,4	63,71	1,091	67,6
6	2,50	70,7	70,98	0,981	68,0

По формуле (12) находим значение максимального урожая красного клевера: А = 73,461 ( В = 32,8). По формуле (13)

находим значения коэффициентов действия ( с i ) на разных интервалах изменения дозы калийных удобрений (0,00– 0,10), (0,10–0,25), (0,25–0,60), (0,60–1,50), (1,50–2,50) и соответствующие расчетные (прогнозные) количества урожая красного клевера по формуле (14); результаты расчетов приведены в таблице 5, где в последнем столбце приведены значения урожая красного клевера по методике Э.А. Митчерлиха, которые определены по уравнению:

lg (А – y) = lg (А – а) – 1,33x, где А – наибольший урожай;

а – наименьший урожай;

с = 1,33 – коэффициент действия фактора роста для калийных удобрений К 2 О).

Среднее значение коэффициента действия фактора роста ( с ) для калийных удобрений по новой цифровой модели равно c̄ = 1,921, а по методике Э.А. Митчерлиха с = 1,33, т. е. в 1,4 раза меньше.

По формуле (17) определим запас питательных веществ в почве (х = х0) для опытных данных (контроль), когда не использовали удобрения, а получили урожай у0 = 32,8 г:

Хо = “ ln| ⁰    1,753

73,461     ] . ( 32,8 + 32,8

1 + In |

73,461 - 32,8 J (    32,8

= 0,733 г .

По формуле (15) определим количество калийного удобрения ( х пр ) для получения, например, урожая у пр = 50 г:

x = 0,733 + — пр           1,753

( 32,8 + 50 Л . ( 73,461 - 50 V lnl---------------I- lnl-------------------I

( 32,8 + 32,8 J ( 73,461 - 32,8 J

= 1,179 г .

Таким образом, запас калийных питательных веществ в почве равен х 0 = 0,733 г, и для получения урожая у = у пр = 50 г необходимо всего использовать х пр = 1,179 г калия, т. е. для значения фактора роста ( х ) можно найти: х = 1,179 – 0,733, или х = 0,446 г, и для урожая у (0,446) по формуле (14) получить:

y ( 0,446 ) =

73,461 ( 32,8 + 32,8 ) exp ( 1,753 ■ 0,446 ) - 32,8 ■ 40,661 ( 32,8 + 32,8 ) exp ( 1,753 ■ 0,446 ) + 40,661

или:

y ( 0,446 ) = ^9198,265 = 49,983 г , 184,029

как и прогнозировалось.

Пример 6. Влияние калия на урожай овса. Рассмотрим результаты опытов, описанные в монографии Э.А. Митчер-лиха [4] (стр. 276, табл. 118), на разных почвах Восточной Пруссии (табл. 6).

Таблица 6

Результаты вегетационных опытов Э.А. Митчерлиха по влиянию калия на урожайность овса на почвах Шенбаллена

№ п/п	Доза К 2 О ( х i ), г	Урожай, опыт ( у i ), г	Урожай, расчет ( у i ), г	Коэффициент действия ( c i )	Урожай, расчет ( ȳ i ), г
1	0,000	17,8	17,80	–	16,5
2	0,108	38,0	38,00	6,659	39,5
3	0,216	58,8	59,32	6,489	56,0
4	0,432	76,5	88,11	3,315	76,4
5	0,648	85,8	88,50	2,415	86,8
6	1,080	97,6	96,46	2,865	95,0

По формуле (12) находим значение максимального урожая овса: А = 103,233 г/со-суд ( В = 17,8). По формуле (13) находим значения коэффициентов действия ( с i ) на разных интервалах изменения дозы калийных удобрений (0,00 – 0,108), (0,108 – 0,216), (0,216 – 0,432), (0,432 – 0,648), (0,648 – 1,080) и соответствующие прогнозные количества урожая овса по формуле (14); результаты приведены в таблице 6, где в последнем столбце приведены расчетные значения урожая овса по методике Э.А. Митчерлиха, которые определены по уравнению:

lg (98 – y ) = lg (98) – 1,33( x + 0,06).

Среднее значение коэффициента действия фактора роста ( с ) для калийных удобрений по новой цифровой модели равно c̄ = 4,349, а по методике Э.А. Митчерлиха с = 1,33, т. е. в 3,3 раза меньше.

По формуле (17) определим запас питательных веществ в почве ( х = х 0 ) для опытных данных (контроль), когда не использовали удобрения, а получили урожай у 0 = 20,7 г:

x » =----- ⁰   5,825

'  (    103,233 V 1 ( 20,7 + 20,7'

ln |--------------|+ ln | — ------—

( 103,233 - 20,7 J    (    20,7

= 0,157 г .

По формуле (15) определим количество калийного удобрения ( х пр ) для получения, например, урожая у пр = 50 г:

x пр

= 0,157 +    '

5,825

( 20,7 + 50 V , ( 103,233 - 50 ' ln |-----------------I - ln |----------------------

( 20,7 + 20,7 J    ( 103,233 - 20,7,

= 0,324 г .

Таким образом, запас калийных питательных веществ в почве равен х0 = 0,157 г, и для получения урожая у = упр = 50 г необходимо всего использовать хпр = 0,324 г калия, т. е. для значения фактора роста (х) можно найти: х = 0,324 – 0,157, или х = 0,167 г, и для урожая у(0,167) по формуле (14) получить:

/    . _ 103,233 ( 20,7 + 20,7 ) exp ( 5,825 ■ 0,167 ) - 20,7 ■ 82,533

^ ’   ’~       (20,7 + 20,7)exp(5,825 ■ 0,167)+82,533      ’ или:

9597,065

y ( 0,446 ) =----- ’---- = 49,972 г ,

192,047

как и прогнозировалось.

Заключение. В качестве основных выводов можно отметить следующие положения.

• 1.    Для оценки степени влияния разных удобрений на урожай сельскохозяйственных растений предложено использовать значение коэффициента действия фактора роста , который численно равен относительной скорости прибавки урожая при равнозначном увеличении количества удобрений (питательных веществ) в почве.

• 2.    Рассмотрены примеры расчетов, иллюстрирующие применение новой цифровой модели роста растений для определения коэффициента действия фактора роста.

• 3.    Проведено определение степени влияния удобрений на урожайность разных сельскохозяйственных растений и установлено, что азотные удобрения оказывают более сильное действие на урожай, чем фосфорные и калийные.

• 4.    Значение коэффициента действия фактора роста зависит от других факторов, потому что рост и развитие растений происходит в разных почвенных и природно-климатических условиях.