Цифровой двойник быстроходной гусеничной машины с бортовым гидрообъёмным механизмом поворота
Автор: Алябьев Вадим Анатольевич, Кондаков Сергей Владимирович, Малаховецкий Алексей Андреевич, Павловская Ольга Олеговна, Растрыгин Сергей Александрович, Черепанов Сергей Игнатьевич
Рубрика: Численные методы моделирования
Статья в выпуске: 1 т.22, 2022 года.
Бесплатный доступ
Статья посвящена исследованию процессов, происходящих в трансмиссии и механизме поворота быстроходного тягача МТЛБу с оригинальной структурой механизма передач и поворота (МПП). Традиционная конструкция зубчато-рычажного двухпоточного МПП дополнена тремя гидромашинами, соединенными двумя гидролиниями. Это позволило тягачу реализовать любой радиус поворота от прямолинейного движения до разворота на месте вокруг центра тяжести. Разработана математическая модель (цифровой двойник) быстроходного гусеничного тягача, с помощью которого удалось выбрать параметры автоматической системы управления движением МТЛБу, обеспечивающей прохождение машиной трассы типа змейки на четвертой передаче, со скоростью 34 км/час, что недостижимо при традиционном МПП этой машины. Проанализированы показатели управляемости движения МТЛБу вблизи границы заноса. Показано, что поворот быстроходной гусеничной машины на границе заноса весьма привлекателен с энергетической точки зрения. Поворот за счет инерционных сил существенно разгружает двигатель внутреннего сгорания и в итоге сокращает расход топлива. Сложность состоит в управлении машиной на границе заноса. В статье показано, что следящая система управления успешно решает эту проблему. В качестве задающего сигнала использована информация о кривизне трассы, которая может формироваться GPS-навигацией или реперными точками на местности. Результатом исследования являются графики изменения параметра регулирования насоса гидрообъёмной передачи, давления в магистралях гидрообъёмной передачи, частот вращения ведущих колес, смещения полюса поворота, характеризующего степень приближения к границе заноса и траекторию движения в декартовых координатах.
Быстроходная гусеничная машина, гидрообъёмный механизм поворота, суммирующий планетарный механизм, бортовой фрикцион, полюс поворота
Короткий адрес: https://sciup.org/147237468
IDR: 147237468 | УДК: 629.3
Текст научной статьи Цифровой двойник быстроходной гусеничной машины с бортовым гидрообъёмным механизмом поворота
Повышение подвижности (управляемости, маневренности, динамики) является актуальной задачей как для технологических тяговых (промышленных тракторов), так и для быстроходных гусеничных машин (БГМ), в том числе специального назначения. Бесступенчатые передачи в трансмиссии гусеничных машин создали элементную базу для решения этой задачи. Теперь, правильно управляя бесступенчатой трансмиссией и механизмом поворота, можно существенно улучшить показатели подвижности гусеничной машины.
Вопросам влияния бесступенчатых трансмиссий и алгоритмов их управления на подвижность БГМ посвящены исследования отечественных и зарубежных ученых [1–11].
Современные БГМ оснащены бесступенчатыми трансмиссиями и механизмами поворота (МП) на базе гидрообъёмных передач (ГОП) [12]. В основном это машины с дифференциальным МП, включающим в себя один насос, один мотор и вал подкрутки [13, 14]. Существуют гусеничные машины с бортовыми гид-рообъёмными МП, состоящими из двух насосов и двух моторов [15–17], а также многопоточные трансмиссии с гидрообъёмной передачей [18, 19]. В данной статье приведены результаты анализа оригинального двухпоточного бесступенчатого механизма поворота, включающего в себя регулируемый гидронасос и два нерегулируемых гидромотора, которые не требуют традиционного, для дифференциальных механизмов поворота, вала подкрутки.
Структурная схема исследуемой гидрообъёмной трансмиссии представлена на рис. 1: ДВС – двигатель внутреннего сгорания; КП – коробка передач; ГН – регулируемый гидронасос; ГМ1 и ГМ2 – нерегулируемые гидромоторы; БФ1 и БФ2 – бортовые фрикционы; СПМ – суммирующие планетарные механизмы.
Эпициклические шестерни СПМ соединены с ДВС через КП. Солнечные шестерни СПМ соединены с ДВС гидромашинами. ГН, ГМ1 и ГМ2 соединены гидравлическими магистралями так, что при нейтральном положении наклонной шайбы насоса ГОП рабочая жидкость свободно циркулируют между моторами. Кроме того, солнечные шестерни суммирующих планетарных механизмов (СПМ) связаны с ДВС через бортовые фрикционы БФ1 и БФ2.
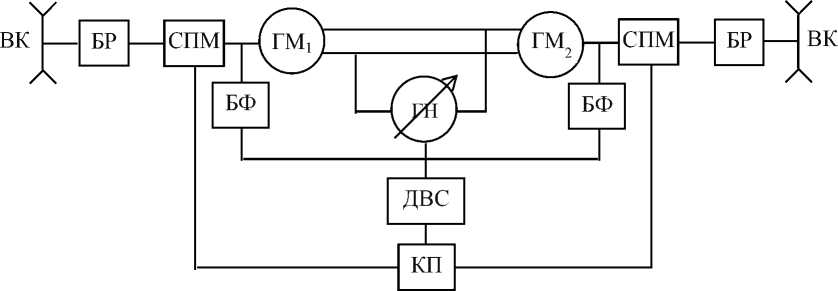
Рис. 1. Структурная схема трансмиссии гусеничной машины
При прямолинейном движении фрикционы замкнуты, солнечные шестерни вращаются с постоянной скоростью, пропорциональной скорости коленчатого вала ДВС. Рабочая жидкость ГОП циркулирует между правым и левым гидромоторами с давлением подпитки, компенсирующей утечки.
При повороте фрикцион отстающего борта выключают и нагрузка перекладывается на мотор ГОП отстающего борта. В гидролинии возникает давление, мотор забегающего борта начинает работать в режиме насоса. Бесступенчатое уменьшение скорости отстающего борта происходит за счет регулирования ГН, который забирает на себя часть подачи мотора забегающего борта.
Принципиальной разницы между магистралями, соединяющими гидромоторы, нет. Однако для математического описания процесса обозначим верхнюю по рисунку магистраль первой, а нижнюю – второй. За положительное направление потока жидкости будем считать направление по часовой стрелке как в контуре гидромоторов, так и гидронасоса. Магистрали могут быть под высоким давлением, могут быть под низким давлением и в процессе движения могут меняться ролями.
Положение наклонной шайбы насоса ГОП и расход насоса ГОП будем считать положительными при движении жидкости по часовой стрелке, и отрицательными – при движении рабочей жидкости против часовой стрелки по рис. 1. Последнее касается только той части круга циркуляции, которая охватывает насос.
Можно представить рассматриваемый гидрообъёмный механизм поворота как три гидромашины, связанные механически с ДВС. Одна гидромашина – регулируемая (на рис. 1 – ГН) и две – нерегулируемые (на рис. 1 – ГМ 1 и ГМ 2 ). При движении машины прямо одна из нерегулируемых гидромашин качает рабочую жидкость в другую нерегулируемую гидромашину. При этом утечки и механические потери компенсируются системой подпитки. Избыточного давления в магистралях нет. Обе нерегулируемые гидромашины вынужденно вращаются с одинаковой скоростью за счет включенных бортовых фрикционов.
При отключении одного из БФ в гидравлической магистрали появляется давление, пропорциональное нагрузке на ведущем колесе отстающего борта. Одна из нерегулируемых гидромашин становится насосом, а другая – мотором. Насос приводится во вращение (как и прежде при прямолинейном движении) включенным БФ (БФ забегающего борта), но теперь он нагружен не только моментом забегающего борта, но еще и моментом, который при прямолинейном движении шел на отстающий борт через включенный БФ отстающего борта. То есть при повороте БФ забегающего борта нагружен двойным моментом, делящимся на две части: одна – механическая, на ведущее колесо забегающего борта, другая – гидравлическая, передающаяся с забегающего борта на отстающий через две нерегулируемые гидромашины.
Уменьшение скорости ГМ отстающего борта обеспечивается «отрицательной» подачей регулируемого насоса (на рис. 1 обозначено как ГН). На самом деле в начале входа в поворот ГН работает как гидромотор, то есть получает давление от ГМ отстающего борта и возвращает крутя- щий момент ДВС, разгружая его. Суммарная производительность ГМ «забегающего» борта и регулируемого ГН уменьшается. Это обеспечивает уменьшение скорости отстающего борта. Мощность торможения отстающего борта возвращается к ДВС через регулируемый ГН.
Система уравнений, описывающая движения гусеничной машины, работу трансмиссии и механизма поворота.
На основе работ [20, 21] и учета особенностей рассматриваемого механизма поворота сформирован цифровой двойник движения гусеничной машины. Он имеет вид системы дифференциальных и алгебраических уравнений, описывающих движение корпуса машины, вращение валов двигателя, насоса и моторов ГОП, давления в магистралях ГОП. Магистралей в данной схеме две, хотя гидромашины три. Ниже приведены только оригинальные уравнения, отличающие мо- дель от существующих в литературе вариантов:
d^H dt
= [ M g i - M к, - М J 2 ]4" •
J 1
d^Ml dt
M м1
—
P 1 R вк
1
iбп (к + 1)J J2 •
d^M2 dt
M м2
P 2 R вк 1
iбп (к + 1)J J3
dP
ГОП1 dt
dP
ГОП2 dt
( Q + Q 1 - Q 7 н м1 м2
( e .2
- Q M1
- Q k11 - Q k21 + Q k31
E
Q k41 •
V1
Q H - Q k12 - Q k22 + Q k32 - Q k42 )~
V2
где t - время, с; ® h, ® Mi , ® M 2 — частоты вращения насоса и моторов ГОП, рад/с; P 1 , P 2 - силы тяги на отстающем и забегающем борту, Н; J 1 , J 2 , J 3 – моменты инерции насоса ГОП, моторов ГОП, кг∙м2; M , M , М , M , M – моменты двигателя, входного вала коробки передач, насоса ГОП, моторов ГОП соответственно, Н∙м; R вк – радиус ведущего колеса, м; i 1 , i 2 , i бп – передаточные числа в трансмиссии; к – параметр суммирующего планетарного механизма; P ГОП1 , P ГОП2 – давления рабочей жидкости в силовых магистралях, МПа; Е – модуль упругости жидкости, Q i – расходы насоса и моторов ГОП, клапанов, дросселей и др., м3/с; V i – объемы соответствующих магистралей м3.
Основные допущения, принятые в математической модели:
– сопротивления повороту считаются по формуле Никитина [22];
– не учтена упругость элементов двигателя, трансмиссии и гусениц;
– не рассмотрены частичные характеристики дизельного двигателя;
– постоянство характеристик грунта в каждом варианте расчета;
– статические характеристики двигателя и гидромашин.
Задающим воздействием в модели является поворот штурвала как функция времени.
Поворот штурвала приводит к изменению моментов на насосе и моторах ГОП по следующим уравнениям:
М = Р ,а и — Р ^а и гопн гоп1qн н гоп2qн н
-^ М гн •
(7) гопм1 гоп1 q м м гоп2 q м м гм1 ,
М ,=P,qu-P,qu -Ш (8)
гопм2 гоп1 qм м гоп2qм м гм2 , где Mгопн и Mгопм1 , Mгопм2 – моменты на насосе и моторах ГОП, Pгоп1 и Pгоп2 – давления в верхней и нижней магистралях ГОП (по рис. 1), qн и q – объёмные постоянные насоса и мотора, uн и uм – параметр регулирования насоса и моторов. В трансмиссии БГМ регулируется насос, связанный через систему управления наклонной шайбой ГОП со штурвалом. Параметр регулирования насо- са при прямолинейном движении равен нулю. При повороте налево он положителен, а при повороте направо – отрицателен. Параметр регулирования моторов остается постоянным и равным единице. Расходы насоса и мотора формируются уравнениями:
Q H = q н u . « он -A Q rH ,
Q м1 q м u м ^ гопм1 A Q гм1 ,
Q м2 q м м гопм2 ^гм2
Потери в гидрообъёмном приводе играют важную роль в достоверности описания работы механизма поворота. В модели использована методика учета потерь, приведенная в работе [23].
Моменты насоса и мотора, определенные уравнениями (9) и (10), входят в правые части дифференциальных уравнений (4), (5), (6). Частота вращения двигателя и насоса ГОП связаны постоянными передаточными числами и определяют момент двигателя по его статической характеристике. Частоты вращения коленчатого вала ДВС и мотора ГОП одновременно определяют частоты вращений ведущих зубчатых колес отстающего и забегающего бортов:
®1 = (^д к / i кп + Юм1 / i 3)/( к + !)/i бр ,
®2 = (Юд к / i кп + ^м2/ i 3)/( к + 1)/i бр .
Если первый борт является забегающим, то
®м! = ®д / i5 , а если отстающим, то
Ю м1
Q m 2 — Q h
а и qм м
Если забегающим является второй борт, то ^ м2 = ® д / i 5 ,
а если отстающим, то
<У „7 м 2
Q m 1 — Q h qм м
Фактические скорости движения, сначала заданные начальными условиями, а затем формирующиеся системой дифференциальных уравнений, сравниваясь со скоростями вращения гусениц, определяют буксования, которые в свою очередь формируют тяговые усилия на забегающем и отстающем борту.
Таким образом, система уравнений (1) – (20) описывает криволинейное управляемое движение гусеничной машины и ее элементов: ДВС, насоса и моторов гидрообъёмной передачи трансмиссии и механизма поворота.
Математическая модель (цифровой двойник) следящей АС управления МП реализована в среде программирование Altair Embed.
Исследования свойств следящей АС управления движением БГМ по её цифровому двойнику проведены в двух характерных режимах:
-
1) прямолинейное движение 100 м, поворот с радиусом 100 м на 90о, прямолинейное движение 100 м;
-
2) движение по трассе, состоящей из трех участков: 100 м – прямо, 100 м – по змейке и 100 м – прямо со скоростями 20 км/час и 34 км/час.
Первый режим. Интерес представляют величина давления при входе в поворот, давление в установившемся повороте и частоты вращения ведущих колес. Результаты приведены на графиках рис. 2 и 3.
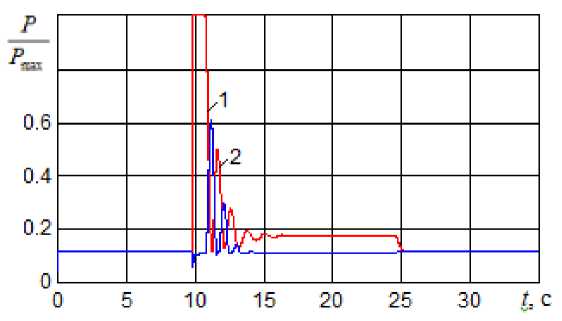
Рис. 2. Относительное давление в магистралях
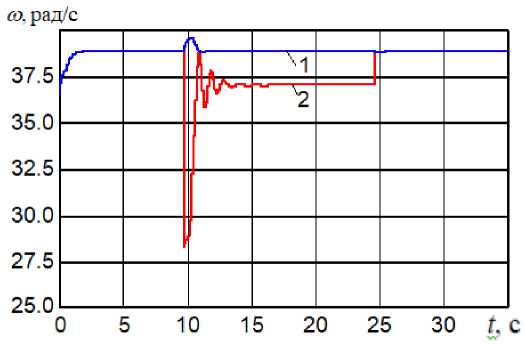
Рис. 3. Частота вращения ведущих колес
Видим, что МТЛБу успешно совершает маневр со скоростью 10 м/с = 36 км/час без перегрузок и без заноса. На рис. 2 – зависимость относительного давления от времени. Относительное давление – это отношение текущего давления к максимально возможному (40 МПа). Из графика следует, что после периода входа в поворот, сопровождающегося перегрузкой по давлению в одной из магистралей в течение 1 с, относительное давление в магистрали нагнетания (1) устанавливается на уровне 0,2, то есть на уровне 8 МПа. Относительное давление в магистрали (2) не превышает 0,6 в переходный период, и практически равно нулю в установившемся повороте. На рис. 3 представлены графики частот вращения ведущих колес. Видно, что частота на забегающем борту равна 39 рад/с, а на отстающем – 37 рад/с, что с учетом буксования обеспечивает радиус в 100 м.
Второй режим. Траектория трассы типа «змейка» задана функцией в декартовых координа- тах:
Y = A sin(kX), где A – амплитуда; k – частота, р/м; X– путь, пройденный по координате X, м.
Задающее воздействие (требуемая кривизна дороги), физически задаваемое поворотом штурвала, при движении по змейке описывается [24] функцией:
K
rд
Y ''
1-'i 1
Ak 2 cos( kX )
1.5 [ 1 + A 2 k 2(cos( kX )) 2 ]1 .5 ,
Управляющее воздействие U формируется по кривизне дороги, как показано на рис. 4. Левый поворот машины (и штурвала управления) математически считаем положительным ( U > 0), а правый поворот – отрицательным ( U < 0).
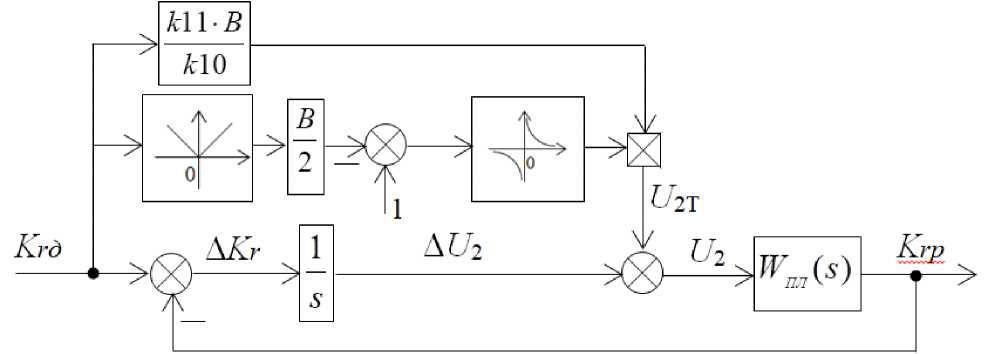
Рис. 4. Структурная схема следящей АС
Фактическая (реальная) кривизна дороги оценивается в режиме online системой по курсовому углу согласно выражению:
_ dy I dt Kp = V- где у - курсовой угол; V - линейная скорость центра тяжести БГМ.
Далее приведены графики, характеризующие качество работы следящей АС управления МП ГМ на различных трассах.
Моделирование движения МТЛБу с бесступенчатым механизмом поворота и автоматической системой слежения за траекторией по трассе «змейка».
Интерес представляет движение по «змейке» на четвертой передаче. МТЛБу с механической трансмиссией и существующим ступенчатым механизмом поворота не мог преодолеть такую трассу. При движении на третьей передаче со скоростью 20 км/час машина проходит «змейку» без проблем. Смещение полюса поворота при 20 км/час меньше половины продольной базы машины (4,06 м), максимальное значение 0,6 м говорит о том, что до заноса далеко. Результаты моделирования движения машины со скоростью 34 км/час приведены ниже. На рис. 5 показаны: 1 – кривизна дороги, 2 – фактическая кривизна траектории центра тяжести машины. По фактической кривизне траектории центра тяжести машины можно судить о границе заноса, она по графику (2) соответствует K = 0,1 , то есть БГМ находится на границе заноса. Важно то, что управляемость при этом не утеряна. На рис. 6 – показано изменение параметра регулирования насоса ГОП: 1 – «теоретический» параметр регулирования, соответствующий кривизне дороги, 2 – фактический параметр регулирования после вмешательства АС.
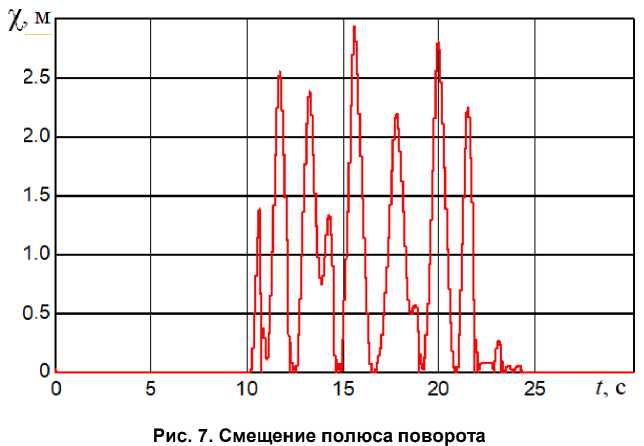
Из рис. 7 видно, что смещение полюса поворота в некоторые моменты превышает 2 м, что свидетельствует о движении ГМ с заносом, но эти моменты не приводят к неуправляемому движению машины. В работе авторов [21] отдельно рассмотрен вопрос о возможности управляемого движения гусеничной машины на границе заноса. При движении на границе заноса ДВС существенно разгружается. Поворот происходит за счет центробежных сил.
Средняя скорость движения за все 300 м трассы составляет 9,55 м/с = 34,38км/час. Устойчивое прохождение «змейки» на скорости 20 км/час занимает 22 с, а на скорости 34 км/час – 12 с. При этом расход энергии ДВС при скорости 20 км/час – 1,88 МДж, а при скорости 34 км/час – 1,42 МДж, то есть на 18 % меньше.
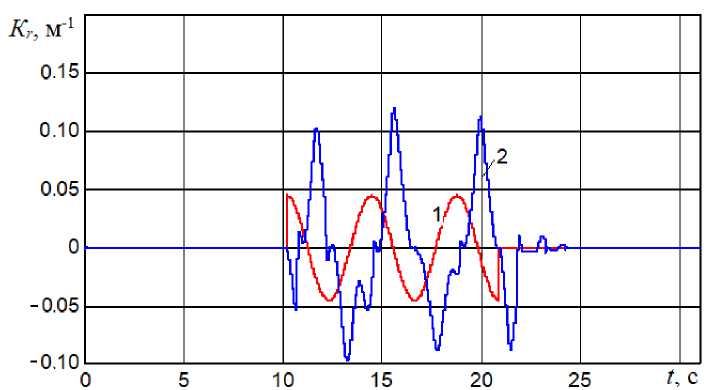
Рис. 5. Кривизна трассы (1), кривизна траектории центра тяжести (2)
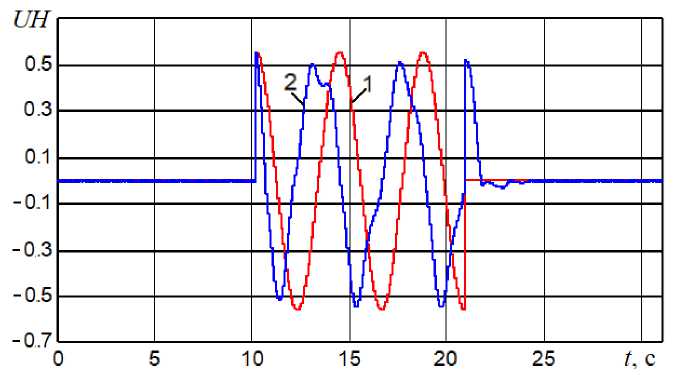
Рис. 6. Параметр регулирования насоса ГОП: (1) – теоретический, (2) – фактический
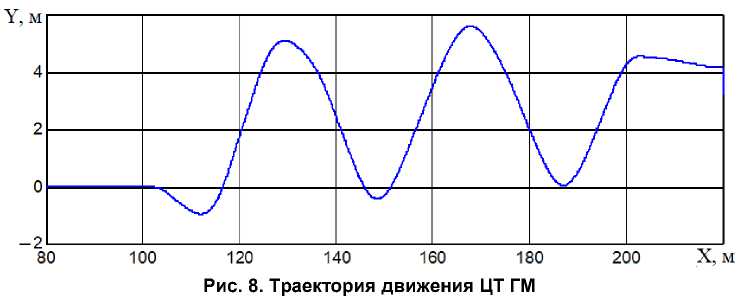
Траектория движения ЦТ ГМ в декартовых координатах при скорости движения ГМ 34 км/час представлена на рис. 8.
Таким образом, внедрение в конструкцию трансмиссии бесступенчатого механизма поворота и автоматической системы слежения за траекторией позволило «справиться» со змейкой на четвертой передаче.
Выводы
-
1. Разработана математическая модель (цифровой двойник) движения гусеничной машины с оригинальной трансмиссией, включающей в себя три гидромашины.
-
2. Получены результаты моделирования нескольких характерных режимов.
-
3. Установлено, что в момент выключения блокировочного одного из бортов, нагрузка начинает передаваться на отстающий борт через мотор (который начинает работать как насос) забегающего борта, то есть механический второй поток мощности заменяется на гидравлический.
-
4. Отработана программа для движения по «змейке» МТЛБу.
-
5. Разработана и апробирована АС слежения за траекторией.
-
6. Установлено, что максимальная скорость для выполнения маневра «змейка» составляет 34,3 км/час.
-
7. Устойчивое прохождение «змейки» на скорости 20 км/час занимает 22 с, а на скорости 34 км/час –12 с. При этом расход энергии ДВС при скорости 20 км/час – 1,88 МДж, а при скорости 34 км/час – 1,42 МДж, то есть на 18 % меньше.
Литературы
Список литературы Цифровой двойник быстроходной гусеничной машины с бортовым гидрообъёмным механизмом поворота
- Красненькое, В.И. Основы теории управляемости транспортных гусеничных машин / B.И. Красненькое - М.: МВТУ им. Н.Э. Баумана, 1977. - 264 с.
- Благонраеое, А.А. Динамика управляемого движения гусеничной машины: Учебное пособие / А.А. Благонравов, В.Б. Держанский // Курган: Изд-во Курганского машиностроительного института, 1995. - 162 с.
- Neumann, V. Tracked vehicle analysis with simulation technologies support / V. Neumann // University of defence - Brno - 2014. - Vol. 2. - P. 20-23.
- Zhai, W. Fundamentals of vehicle-track coupled dynamics. / W. Zhai, K. Wang, C. Cai // Vehicle System Dynamics. - 2009. - Vol. 47. - P. 1349-1376. D01:10.1080/00423110802621561
- Sojka, M. Tracked vehicle movement modelling / Michal Sojka, Stefan Cornak // University of Defence in Brno. - 2018. - P. 2098-2103. DOI: 10.22616/ERDev2018.17.N358.
- Chen, C. Dynamic Modeling of Tractor-Semitrailer Vehicles in Automated Highway Systems / C. Chen, M. Tomizuka // Department of Mechanical Engineering University of California, Berkeley, USA, 1995.
- Murakami, H. A mathematical model for spatial motion of tracked vehicles on soft ground / H. Murakami, K. Watanabe, M. Kitano // Journal of Terramechanics. - 1992. - Vol. 29. - P.71-81.
- Чобиток, В.А. Теория движения танков и БМП: Учебник / В.А. Чобиток. - М.: Военное издательство, 1984. - 263 с.
- Earl J. Tanks, Tear Gas, and Taxes: Toward a Theory of Movement Repression. / Jennifer Earl //Sociological Theory. - 2003. - Vol. 21, № 1. - P. 44-68. D0I:10.1111/1467-9558.00175
- 10.Gorton, G.B. Special Purpose Vehicles and Securitization / Gary B. Gorton, Nicholas S. Souleles // FRB Philadelphia Working Paper - 2005. - № 05-21. http://dx.doi.org/10.2139/ssrn.713782
- Motion control of tracked vehicle based on contact force model / Shotaro Koji-ma; Kazunori Ohno; Takahiro Suzuki; Thomas Westfechtel; Yoshito Okada; Satoshi Tadokoro // International Conference on Intelligent Robots and Systems, South Korea, 2016 - P. ¡¡77-1183. DOI:¡0.1109/IROS.2016.7759198
- Буров, С.С. Конструкция и расчет танков / С.С. Буров. - Изд. Академии БТВ. 1973. -602 с.
- Военные гусеничные машины: учебник в 4-х томах / под ред. В.С. Старавойтов. - Т. 1. Устройство. Кн. 2. -М.: МГТУ им. Н.Э. Баумана, 1990. - 336 с.
- Чобиток, В.А. Конструкция и расчет танков и БМП: Учебник/ В.А. Чобиток - М. : Военное издательство, 1984. - 375 с.
- Малютин, Л. RoadShow 2006 по версии Liebherr. URL: https://os1.ru/article/5775-roadshow-2006-po-versii-liebherr (дата обращения 20.02.2022).
- Гусеничный бульдозер Liebherr PR744BL Litronic. URL: https://www.euronato.ru/ card/vsya_texnika/dorozhno-stroitelnaya_texnika/buldozery_gusenichnye/gusenichnyj_buldozer_ liebherr_pr744bl_litronic/(дата_обращения 20.02.2022).
- Отличительные особенности бульдозера ТМ10 ГСТ ДСТ Урал. Форма доступа https://aservicedst.ru/blog/otlichitelnye-osobennosti-buldozera-tm10-gst-dst-ural/ (дата обращения 20.02.2022).
- Пат. 0004427 Европейская патентная организация,. Four forward range hydro mechanical steering transmission /Reed Oliver Bradley [США]. Заявл. 21.03.1978; опубл. 03.10.1979. - 24 с.
- Вансович, Е.И. Способы снижения установочной мощности гидрообъёмной передачи в механизме передач и поворота дифференциального типа/Е.И. Вансович//Вестник ЮУрГУ серия Машиностроение. - 2012. -Т. 19, №12. - С. 107-114.
- Кондаков, С. В. Автоматизированное управление движением быстроходной гусеничной машины: Монография / С.В. Кондаков, О.О. Павловская. - Саарбрукен: Академическое издательство ЛАП ЛАМБЕРТ, 2013. - ¡05 c.
- Кондаков, С.В. Повышение подвижности быстроходной гусеничной машины на основании алгоритма управляемого заноса. / С.В. Кондаков, О.О. Павловская, И.В. Иванов и др. //Вестник машиностроения. - М. : Машиностроение. - 2020. - № 12. - С. 29-33.
- Никитин, А.О. Теория танка / А.О. Никитин, Л.В.Сергеев. - Изд. Военная академия бронетанковых войск. 1962. - 584 с.
- Объёмные гидромеханические трансмиссии / Под ред. Е.С. Кисточкина. - Л.: Машиностроение, 1987. - 256 с.
- Бронштейн, И.Н Справочник по математике для инженеров и учащихся вузов / И.Н. Бронштейн, К.А. Семендяев // Под редакцией Г. Гроше, В. Циглера, пер. с немецкого. -Лейпциг: Тойбнер, 1979. - М.: Наука. Главная редакция физико-математической литературы, ¡980. - 976 с.


