Цифровые модели повреждаемых стержневых систем для интеллектуальной поддержки их жизненного цикла

В настоящее время общепризнана фактическая невозможность обеспечения безотказности технических объектов в течение их жизненного цикла (ЖЦ). Это связано с протеканием естественных деградационных процессов накопления повреждений [1], невозможностью учёта на стадии проектирования всех возможных воздействий и событий, оказывающих влияние на работоспособность объектов, исключения дефектов конструкционных материалов при изготовлении [2]. Под повреждаемыми понимаются конструкции, в которых на стадии эксплуатации нарушаются условия прочности, возникает, развивается и завершается процесс разрушения, в результате чего конструкция становится повреждённой. Свойства конструкций в повреждённом состоянии слабо изучены и высока опасность непрогнозируемого их поведения, приводящего к нарушению работоспособности, в т.ч. к тяжёлым авариям и катастрофам. В связи с этим актуальны исследования, направленные на изучение свойств повреждаемых конструкций и возможностей включения этих результатов в информационную поддержку ЖЦ технических объектов. Создание цифровых моделей (ЦМ) позволяет осуществлять систематизацию и хранение данных о свойствах повреждаемых конструкций с учётом дискретности принимаемых во внимание факторов и накопленных повреждений.

В настоящей работе для стержневых систем рассматривается взаимосвязь способов имитации разрушения структурных элементов и типов задач, решаемых в течение ЖЦ объектов. От способа имитации разрушения структурных элементов зависит объём и достоверность оценок свойств повреждённых конструкций, что предопределяет возможность использования этих результатов для информационной поддержки задач управления их ЖЦ.

1 Взаимосвязь цифровых моделей и ситуаций принятия решений

Необходимость анализа поведения повреждаемых стержневых систем (ПСС) возникает на стадии их эксплуатации. Информационное обеспечение принятия решений с использованием предварительно подготовленных ЦМ основано на получении решения сложных ресурсоёмких задач анализа напряжённо-деформированного состояния ПСС до момента необходимости использования ЦМ. Эффективность применения ЦМ для информационной поддержки оценки уровня накапливаемых повреждений на стадии эксплуатации показана, например, в [3]. Информационная поддержка принятия решений с использованием заранее подготовленных ЦМ применяется для управления ЖЦ гидроагрегатов [4].

Взаимосвязь ЦМ и ситуаций принятия решений показана на рисунке 1.

Рисунок 1 - Взаимосвязь цифровых моделей и ситуаций принятия решений

В ситуации принятия решения возникает ряд задач, которые определяют целесообразность одного из альтернативных вариантов действий. Решению этих задач предшествуют формулировка перечня вопросов и содержания ответов на них, а также требований к ЦМ, которые должны обеспечивать получение необходимых ответов. Эти ответы получаются путём создания и применения соответствующих ЦМ. Результаты исследований ЦМ могут быть многократно использованы в ситуации быстрого принятия решений в практических задачах.

В качестве одной из типовых ситуаций для ПСС рассматривается разрушение структурного элемента стержневой системы. Для формализации определены следующие множества.

Множество задач принятия решений A ={ a 1 , a 2 , a ₃} содержит три элемента: оценка работоспособности повреждённой конструкции ( a 1 ), оценка необходимости ремонтновосстановительных работ ( a ₂), определение сценария аварийного разрушения ( a ₃).

Множество B= { b 1 , b ₂, b ₃, b 4 , b ₅} включает в себя следующие вопросы:

• ■    каковы напряжённое состояние и остаточная прочность конструкции при статическом нагружении? ( b 1 );

• ■    каковы пиковые напряжения и характер колебаний при динамическом нагружении? ( b ₂);

• ■    каков характер переходного процесса в момент разрушения стержня и не влечёт ли он каскад разрушений других структурных элементов? ( b ₃);

• ■    необходимо ли удалять фрагменты разрушенного стержня? ( b ₄);

• ■    необходимо ли восстанавливать целостность разрушенного стержня? ( b 5 ).

Для ответов на эти вопросы необходимо получить информацию о напряжённом состоянии повреждаемой конструкции. В связи с этим в множество C={c1, c2, c3, c4, c5} включены следующие требования к содержанию ЦМ – характеристики напряжённого состояния кон- струкции при:

• ■    статическом нагружении с учётом изменения жёсткости вследствие разрушения стержня ( с 1 );

• ■    статическом нагружении с учётом изменения жёсткости и массы вследствие удаления фрагментов разру шившегося стержня ( с 2 );

• ■    динамическом нагружении с учётом изменения жёсткости вследствие разрушения стержня ( с 3 );

• ■    динамическом нагружении с учётом изменения жёсткости и массы вследствие удаления фрагментов раз рушившегося стержня ( с 4 );

• ■    импульсном нагружении вследствие мгновенного разрушения стержня ( с 5 ).

В предположении, что каждому требованию соответствует своя ЦМ напряжённого со стояния, множество D, так же как и

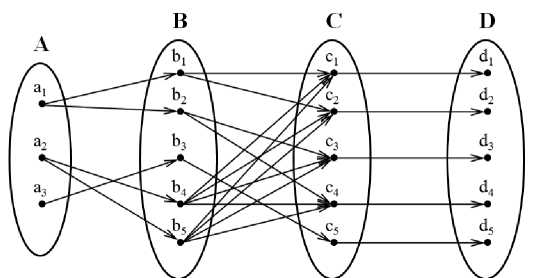
Рисунок 2 – Соответствия между множествами

множество C, состоит из пяти элементов: D= { d 1 , d 2 , d 3 , d 4 , d 5 }. Каждая ЦМ в общем случае представляет собой структурированный массив максимальных эквивалентных напряжений σ ij в i -м стержне при разрушении j -го стержня: d =(σ ij ), i =1, n , j =1, n , где n – количество стержней в системе.

Соответствие между рассматриваемыми множествами (рисунок 2) конкретизирует общий вид взаимосвязи (рисунок 1) для ПСС.

• 2    Имитация разрушения структурных элементов стержневых систем

Для выполнения требований (множество C ) к содержанию ЦМ (множество D ) на стадии их создания и исследования необходимо использование аппарата, позволяющего отразить особенности поведения ПСС в момент разрушения её структурного элемента и в период после разрушения. Для анализа поведения ПСС используются методы механики деформируемого твёрдого тела, геометрические модели, создаваемые в программных комплексах автоматизированного проектирования ( CAD -пакетах), и численные (конечно-элементные, КЭ) модели, создаваемые в программных системах инженерного анализа.

Возможно применение двух технологий моделирования разрушения стержней: удаление стержня целиком из расчётной схемы (модели) [5-10]; его виртуальное рассечение в поперечном сечении, путём модифицирования геометрической модели (разрезание стержня) средствами используемого CAD -пакета или применением к КЭ модели универсальной вычислительной технологии «рождения и смерти элементов» (РСЭ) 1 [11, 12]. Технология РСЭ применяется для моделирования разрушения и повреждения различной природы [11-15] и изменения конфигурации технического объекта при его создании [16]. Она заключается в мгновенном изменении (увеличении при «рождении» или уменьшении при «смерти») жёсткости КЭ. При мгновенном уменьшении жёсткости в «разрушаемом» сечении стержня (одном или нескольких КЭ) он остаётся в КЭ модели (сохраняя неизменным распределение массы), но перестаёт сопротивляться деформациям (что равносильно исключению из силовой схемы).

1ANSYS 2022R1 Documentation. Houston: SAS Inc., 2022.

1                   3                   2

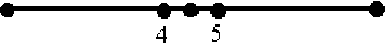
1, 2 – концевые точки стержня; 3 – точка «разрезания» стержня, 4, 5 – узловые точки конечного или структурного элемента с уменьшенным значением модуля Юнга

Рисунок 3 – Схема модификации разрушаемого структурного элемента

Указанные технологии поясняются следующей схемой (рисунок 3). Первоначально целостный структурный элемент ограничен точками 1 и 2. Анализ конструкции с удалённым стержнем предполагает исключение стержня 1-2; с рассечённым стержнем – замену стержня 1-2 парой стержней 1-3 и 3-2 с разрывом связи в точке 3. По технологии РСЭ возможны следующие варианты. В разрушаемом сечении стержня 1-2 генерируется «умирающий» КЭ 4-5 с пониженным модулем Юнга. В некоторых случаях возникает необходимость имитировать технологию РСЭ на геометрической модели. Тогда исходный стержень 1-2 разделяется на три стержня 1-4, 4-5 и 5-2 с заданием для стержня 4-5 свойств материала с уменьшенным модулем Юнга.

Эти технологии могут быть применены к различным типам моделей конструкции: удаление и разрезание стержня возможно только в геометрической (до начала процесса решения), применение технологии РСЭ – в КЭ модели непосредственно в процессе решения задачи.

• 3    Схема построения цифровых моделей повреждаемых стержневых систем

В настоящем исследовании предполагается работа конструкционного материала в упругой стадии деформирования (запасы прочности неповреждённой конструкции соответствуют нормам проектирования, разрушение стержня является хрупким), что позволяет не учитывать влияние фактора физической нелинейности материала на выбор технологий анализа. Перемещения, возникающие при разрушении стержней, априори не могут считаться малыми, что требует учёта геометрической нелинейности. Разрушение стержней означает изменение расчётной модели конструкции, что является конструктивной (структурной) нелинейностью.

Рассматриваемый тип конструктивной нелинейности порождает динамический процесс, который не может быть исследован в статической постановке. Однако возможно исследование конструкции после завершения динамического процесса, т.е. в статической постановке возможен анализ повреждённых конструкций. Варианты учёта конструктивной нелинейности при построении ЦМ ПСС показаны на рисунке 4.

Геометрически нелинейный статический силовой анализ повреждённой конструкции при разрезании стержня учитывает изменение только жёсткости ПСС и обеспечивает выполнение элемента c 1 множества требований к ЦМ. Этот вариант даёт адекватный физическому состоянию конструкции результат после разрушения стержня (остающегося в ПСС), порождающего дополнительные силовые факторы от изгиба фрагментов разрушившегося стержня.

Геометрически нелинейный статический силовой анализ повреждённой конструкции при удалении стержня учитывает изменение массы и жёсткости ПСС и обеспечивает выполнение элемента c 2 множества требований к ЦМ. Этот вариант соответствует состоянию ПСС после физического удаления фрагментов разрушившегося стержня.

Геометрически нелинейный анализ вынужденных колебаний повреждённой конструкции при удалении и разрезания стержня учитывает изменение отклика вследствие изменения динамических характеристик из-за уменьшения массы и жёсткости (выполнение требования c 4 ) или только жёсткости (выполнение требования c 3 ) повреждённой конструкции.

Геометрически и структурно нелинейный анализ переходных процессов ПСС обеспечивает анализ её поведения в момент разрушения и непосредственно после него. Получаемые результаты соответствуют элементу c 5 множества требований к ЦМ.

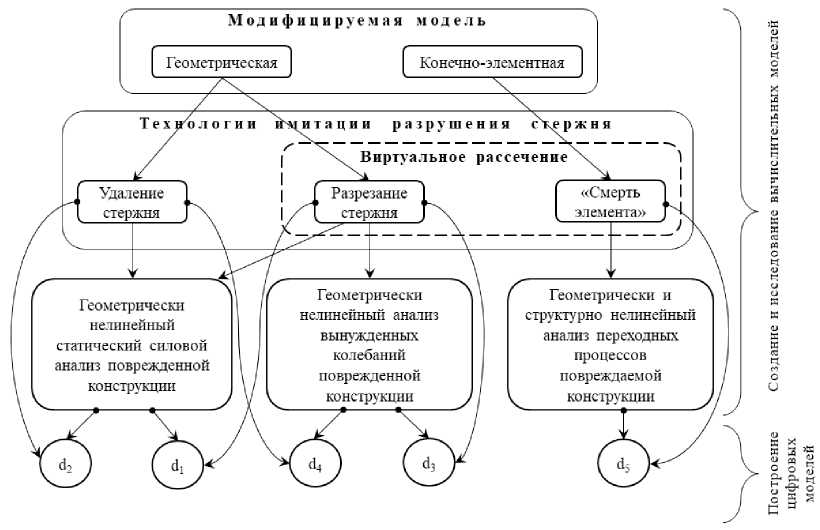
Рисунок 4 – Схема построения цифровых моделей повреждаемых стержневых систем

Таким образом, ЦМ можно рассматривать как продукт систематизации результатов, полученных с использованием рассмотренных технологий имитации разрушенных структурных элементов и выбираемых в связи с необходимостью быстрого получения ответов на заранее сформулированный перечень вопросов.

• 4    Численный пример

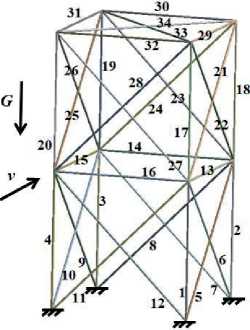
В качестве модельной задачи рассматривается стальная пространственная стержневая система рамного типа с жёсткой заделкой в четырёх точках. Система содержит 34 стержня (рисунок 5 а ), каждый из которых может быть разрушен. Статическая нагрузка представлена собственным весом G , динамическая – боковым ветром, скорость которого предполагается случайной величиной со значением, характерным для местности размещения конструкции (рисунок 5 б ). В качестве такого значения принята скорость ν = 25 м/с.

б )

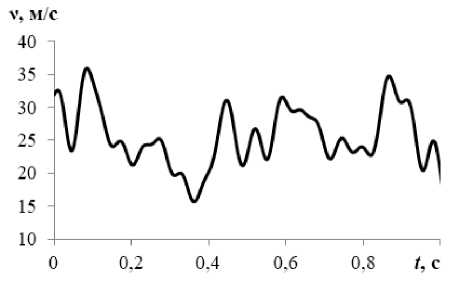
Рисунок 5 – Схема модельной задачи: а) конфигурация стержневой системы; б) характерный фрагмент изменения скорости ветра ν

Компьютерное моделирование динамического нагружения ветром выполнено следующим образом. Статистические исследования [17] скорости ветра независимо от географического расположения местности, высоты над поверхностью почвы и особенностей ландшафта показали, что адекватной вероятностной моделью является закон Вейбулла с функцией распределения

(

F ( ^v ) = ¹ — exp <  где g - параметр масштаба; h - параметр формы.

м * ]

< ^g J I

,

Установлено [17], что в большинстве случаев параметр формы близок к 2. Известно [18], что для распределения Вейбулла математическое ожидание случайной величины определяется с использованием гамма-функции Г как v = g • г (( h + 1 )/ h ) . Тогда из равенства V = 25 = g • г (( 2 + 1 )/ 2 ) можно найти значение параметра масштаба g = 25/ г( 1,5 ) ~ 28,1 .

Случайные числа для распределения Вейбулла W : g , h получаются из случайных чисел для равномерного распределения R на интервале [0,1] с помощью соотношения [18]: W : g , h ^ g • ( - log R ) 1 ^h . Фрагмент сгенерированной таким образом временной зависимости скорости ветра v = f( t ) показан на рисунке 5 б .

Давление воздушного потока p (Па) в связи со скоростью ветра v (м/с) определяется известным выражением p = р v ² /2 ( р - плотность воздуха, кг/м ³ ). В каждый момент времени это давление приложено ко всем стержневым элементам ПСС с учётом угла их наклона по отношению к направлению ветра.

Выполнено пять серий вычислительных экспериментов (каждая серия - отдельная ЦМ), в ходе которых осуществлена имитация разрушения каждого структурного элемента с определением максимальных напряжений о ц во всех элементах (в т.ч. в разрушенном, если он не удаляется из ПСС). Вычисления выполнены в геометрически нелинейной постановке с использованием пакета КЭ анализа ANSYS : цифровые модели d i , d 2 получены в модуле Static Structural , d ₃, d 4 , d 5 - в модуле Transient Structural . Визуализация цифровых моделей в виде набора таблиц показана на рисунке 6.

Каждый столбец в таблице соответствует i -му структурному элементу модельной конструкции, каждая строка - разрушению j -го структурного элемента. Каждая ячейка таблицы содержит значение эквивалентного напряжения O j : например, для ЦМ d ₅ в процессе разрушения третьего структурного элемента ( j' = 3) во втором структурном элементе ( i = 2) максимальные эквивалентные напряжения составляют о₂₃ = 55 МПа.

Сравнение значений о ij с величиной временного сопротивления конструкционного материала о b представляет собой известный критерий прочности о ij < о b . Возможны два варианта результата оценки: o ij < о b - прочность обеспечена; о ij > о b - не обеспечена.

Использование полученных ЦМ совместно с критерием прочности в случае разрушения j -го структурного элемента позволяет принять решение о работоспособности повреждённой конструкции (работоспособна, если о _ij < о b , i = 1, n ), необходимости ремонтновосстановительных работ (необходимы, если о ij > о b , i = 1, n ), возможности возникновения каскадных разрушений конструкции (возможны, если о ij > о b , i = 1, n ). Для принятия решения необходимо извлечение из имеющихся ЦМ значений о ij и установление одного из двух вариантов выполнения критерия прочности.

Таким образом, построенные ЦМ, обеспечивая исходные данные для анализа условий прочности элементов ПСС, позволяют получить быстрые и достоверные ответы на вопросы множества B и обосновать решения задач множества A .

Цифровая модельdl

■19

Цифровая модельd2

Ч

5 5

S3

Цифровая модельd3

ю

S3

S3 Цифровая модель d4

S1

S1

S3

19 | 20 | 21 рГ

ТГГгдТТГГйГртГгвТгэТз^

54 Цифровая модельd5

JZ 8 52 49

87 103

ю

_72

•17

ЬЗ

S3

52 68

S3

53 68

68 53 52

53 53

S2 55

55 53

52 54

S3

S3

5S

'мГ

97 81

88 10S

84 83

95 86

80 81

80 84

86 103

80 81 80^ 23«

80 105

8-1

85 ’so’

• ■ :

103 82 "sT

80 189

■9

"so”

В1

• ■ -

• ■'

86 S ■

ТГ

s )

105 108

130 130

10 7 168

6S

65 68 ПО

69 65

68 66

65 76

S2 ПО

69 189

65 цЦ

107 / •

ПО 82

•Л

-

69 75 74 •4

ПО 82 66 68 76 65 18'1 71 • '■ 69 72 74 72 69 107 73

74 ПО

76 189

69 ПО /4

65 76

102 80

60 58

-

-

•S3

.■

58 66

:- 78 78

-:

SU 80 ...;

61 116 58

59 63

64 80

80 «И

61 161

Рисунок 6 – Визуализация цифровых моделей напряжённого состояния повреждаемой конструкции

Заключение

В статье рассмотрен частный случай ПСС, характеризующийся хрупким разрушением отдельных структурных элементов. Предпосылкой построения ЦМ таких систем послужила декомпозиция проблемы принятия решений, касающихся повреждаемой конструкции, и представление её в виде группы трёх задач, для каждой из которых установлена однозначная взаимосвязь с технологиями имитации разрушения стержневых элементов и соответствующих вычислительных моделей. Полученные на этой основе ЦМ представляют собой результат интеллектуальной деятельности, выраженный в законченной самостоятельной форме. Это позволяет считать использование таких ЦМ интеллектуальной поддержкой эксплуатации как одной из стадий ЖЦ ПСС.