Циклические подгруппы полной линейной группы второй степени над полем нулевой характеристики

В данной работе дается описание циклических подгрупп полной линейной группы GL 2 (F ) над любым полем F нулевой характеристики. Тем самым нами дается усиление основного результата из [1], относящегося только к случаю алгебраически замкнутого поля F (и значит, например, случай поля рациональных чисел F = Q выпадет из рассмотрения).

Итак, пусть F — произвольное поле нулевой характеристики,

M = a^a b) _G GL 2 (F).

cd

Характеристическое уравнение матрицы M есть x — (a + d)x + ad — bc = 0, а ее характеристические корни a = 2 ^a + d + ^(a — d) + 4bc^ , в = 2 ^a + d — ^(a — d)2 + 4bc.

По теореме Гамильтона — Кэли матрица M является корнем ее характеристического уравнения, т. е.

M ² — (a + d)M + (ad — bc)E = 0,                       (1)

„   (1 0\                        n /0 0\ где E = I 0 i I — единичная матрица, 0 = I 0 0 ) — нулевая матрица.

В силу (1) для любого натурального n >  2 имеем рекуррентное уравнение для степеней матрицы M :

M n = (a + d)M n -1 + (bc — ad)M n ^{- 2} .                       (2)

(c) 2011 Жемухова М. З., Пачев У. М.

Если матрица M — вырожденная и, значит, M / GL 2 (F ), det M = 0, то в этом случае из (2) получаем

Mn = (a + d)M n-1, откуда

M n = (a + d) ^n-1 M, n >

Следовательно, в случае вырожденной матрицы M полугруппу, которую как и в случае циклических групп полученному результату имеем получаем только циклическую обозначим через hMi. Согласно

hMi = {(2SpM)n-1| Vn G N}, где Sp M = a + d — след матрицы M = ^a dj .

Пусть теперь M G GL 2 (F), и значит det M = ad — bc = 0. Тогда соотношение (2) есть рекуррентное уравнение второго порядка для степеней матрицы M (обычно рекуррентные уравнения встречаются только для числовых последовательностей).

В случае матрицы M G GL 2 (F) наиболее удобное описание циклических подгрупп h M i полной линейной группы GL 2 (F) получается с помощью характеристических корней матрицы M .

Следуя [1], рассмотрим сначала случай различных характеристических корней b d.

(a = в ) матрицы M = ^a

Тогда имеем a + в = a + d, ав = ad — bc, и значит в силу (2) получаем откуда

Следовательно,

M ⁿ

_M n _-

M ⁿ

= (a + в ) M n ^-1 + авM n ^-2 ,

вM n -1 = a (M n -1 — вM ^{n- 2})

.

-

вM n -1 = a n ^-1 (M — вЕ ),

где M 0 = E — единичная матрица, и аналогично этому

M ⁿ - αM ^n-1

в n -1 (M - aE ).

Из (4) и (5) для любого натурального n

почленным вычитанием находим, что

ab cd

ⁿ   α ⁿ - β ⁿ

α - β

a

c

b d

-

α αβ

n -1

-

_β n -1

α - β

E.

В силу основной теоремы о симметрических многочленах (справедливой для многочленов над целостным кольцом [2]) коэффициенты в (6), на которые умножаются матрицы, принадлежат полю F и поэтому нет необходимости считать поле F алгебраически замкнутым.

Перейдем теперь к случаю кратных характеристических корней матрицы M = (a d), т. е. случаю a = в .В этом случае в заметке [1] для вычисления M использовался предельный переход при β → α, что требует полноту поля F (но это условие опять не выполняется, например, для поля Q). В этом случае наиболее подходящим является рассуждение, использующее индуктивный способ определения Mn.

Итак, в силу (3) при n = 2 в случае кратных характеристических корней имеем:

M ² = 2aM — a ² E.

Опираясь на это соотношение, получаем, что

M n = na n -1 M — (n - 1) a n E.

Эту формулу можно записать в явном виде через элементы поля F :

M ⁿ = n

a + d 2

n -1

M — (n —

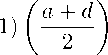
n

E.

Формулы (6) и (7) справедливы и при n <  0, если учесть, что

M - m = ⁽ M ^-1 ) m = (M m ) ^-1 (m E M ).

В [1] основной результат о циклических подгруппах h M i в случае различных характеристических корней получен при ограничительном условии n = 0. Это ограничение мы снимаем через использование функции sgn n — знак числа n. Если обозначим

a

c

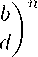
a n c _n

b _n d n

n ∈ N ,

то в случае различных характеристических корней получаем

	α n - β n        α n -1 - β n -1
a n	a - αβ α - β         α - β
b n	α n - β n b, α - β α n - β n
c n	α - β c,
d n	α n - β n        α n -1 - β n -1 d - αβ α - β         α - β

Еще более простые выражения получаются для этих элементов в случае кратных характеристических корней, а именно an bn \ = Anan 1a — (n — 1) an        nan 1b      \      = a + d cn dn)           nan-1c        nan-1d — (n — 1) an) , a 2

Полученный основной результат дает усиление доказанной в [1] теоремы о циклической подгруппе h M i полной линейной группы GL 2 (F ).

Теорема 1. Циклическая подгруппа hMi, порожденная любым элементом M = b d

a

c

группы GL2(F) над полем F нулевой характеристики, определяется равенства- ми:

• 1)    M ⁿ = ^a _a - в M ^sgnn — ав ^{al 1} _а ^{— 1} — E, Где a = в, — характеристические корни матрицы M, sgn n — знак числа n;

• 2)    M ⁿ = na ^n-sgnn M ^sgnn — ( | n | — 1) a ⁿ E при a = в = ^a +2 d •

Доказанная теорема 1 дает явное описание бесконечных циклических подгрупп полной линейной группы GL2(F) над произвольным полем F c char F = 0. Но некоторые конечные циклические подгруппы в GL2(F) могут быть построены, например, в том случае, когда поле F = K(n), где K(n) — n-круговое поле над произвольным полем K нулевой характеристики.

Итак, пусть M = (°

d j Е GL2 {K(n)) и £ — один из первообразных корней n-ой степени из 1к, где 1к — единичный элемент поля K. Пусть матрица M Е GL2(K(n))

такова, что ее характеристические корни равны £m£ m, где 1 6 m 6 n, НОД (m, n) = 5. Если теперь t — порядок элемента £m, то £mt = 1, откуда получаем следующие условия делимости

n | mt ^ n

t.

Отсюда, ввиду того, что t должно иметь наименьшее возможное значение, следует, что t = n .

δ

Положив теперь в теореме 1 характеристические корни матрицы M равными а = £ ^m и в = £ ^-m , найдем, что M ( mn ) = E, где (m,n) = НОД (m,n).

Действительно, имеем

n

M ( _т,_п ) =

n

(£ ^m ) ( m,n )

n

_— (£ ^-m ) ( m,n )

ξ ^m

-

ξ - m

M

-

n

(£ ^m ) ( m,n ) ¹

ξ ^m

= OM

-

ξ

-

m

-

ξ ^m

ξ ^m

-

ξ - m

E = E,

n

_— (£ ^-m ) ( m,n ) ¹

-

ξ - m

E

при этом учитывалось, что

C ( mnn ) = £ m ( mnn ) =1 k ,   £^m - ^ ^-m =0.

Значит, h M i — конечная циклическая подгруппа порядка ( mnn ) группы GL 2 (K ⁽ⁿ⁾ ).

Таким образом, нами доказана следующая

Теорема 2. В полной линейной группе GL 2 (K ^{( n )} ) над n-круговым полем K ^{( n )} произвольного поля K нулевой характеристики существует циклическая подгруппа h M i порядка ( mn^ ) , где матрица M имеет своими характеристическими корнями £ ^m и £ ^{- m} , £ — первообразный корень степени n из единицы над полем K; 1 6 m 6 n.

Приведем пример конечной циклической подгруппы в полной линейной группе GL 2 (F ), где F = Q( nT) — круговое поле деления окружности на n равных частей. Тогда для элемента M Е GL 2 (F )

M =

cos ^2п

n

. 2п

— sin — n

— sin ^2п n

2п cos — n

получаем циклическую подгруппу h M i = { M ^K | 0 6 K 6 n — 1 } , порядка группы GL 2 (F ).

Представляет большой интерес перенесение полученных результатов на полные линейные группы степени n >  2 (см. [6]) и на поля простой характеристики, например, на предельное поле Q p = lim n _?^ Fp ^n! , являющееся алгебраически замкнутым полем характеристики p (нужные для этого предварительные сведения можно найти в [3–5]).