Циклическое обогащение гелием природного газа в колонке со стеклянными микросферами

• 1.    Введение

• 2.    Формулировка задачи, ее решение и результаты

В работе [1] исследовалось течение метано-гелиевой смеси в слое полых стеклянных микросфер, которые селективно поглощают гелий, в то же время метан остаётся в объеме колонки и не проникает в полости микросфер. Выявлены два предельных режима, в которых может происходить процесс совместного заполнения колонки газовой смесью и поглощения микросферами гелия: 1) равновесный (волновой), когда поглощение гелия осуществляется одновременно с движением по колонке волны полного давления с формированием волн концентрации метана и гелия; 2) замороженный (объемное поглощение гелия), когда газодинамический процесс заполнения колонки протекает отдельно от процесса поглощения гелия микросферами — сначала вдоль колонки проходит волна давления, и лишь после установления однородного распределения параметров смеси вдоль слоя микросфер происходит поглощение ими гелия). В зависимости от параметров системы возможен тот или иной режим работы колонки, включая множество промежуточных вариантов.

Разделение смесей или их обогащение целевым компонентом на установках, в которых ключевым элементом является одна или несколько колонок со стационарным слоем твердой фазы, обычно происходит в квазиравновесном периодическом режиме, имеющем стадию высокого давления, когда происходит поглощение частицами целевого компонента, стадию низкого давления, когда целевой компонент извлекается из слоя частиц и отводится в ёмкость и ряд промежуточных стадий (возрастания давления на входе, сброс давления за счёт отвода основной массы исходной смеси и др.). Как правило, процесс состоит в повторении стадий с постоянным временным периодом. Характеры протекания нескольких первоначальных периодов при запуске установки

имеют незначительные отличия, а затем происходит выход на стационарнопериодический режим, при котором характеристики системы в моменты времени, различающиеся на один или несколько периодов, остаются неизменными [2, 3].

В настоящей работе представлены результаты расчетов изменения параметров газовой смеси вдоль оси колонки при стационарно-периодическом режиме работы, то есть давление на входе и выходе колонки периодически изменялось. В качестве примера бралась смесь, состоящая из гелия и метана в объемной пропорции 0,005:99,995. Температура системы равнялась 450ºК. Процесс осуществлялся таким образом, что давление смеси на входе в колонку возрастало от 0,1 до 10 МПа в течение времени т 1 . Затем, в течение т 2 оно поддерживалось постоянным (10 МПа). После этого, в течение времени т ₃ , происходило снижение давления до 10 5 Па и удержание на этом уровне в течение т 4 . Подобное изменение давления на входе повторялось с периодом т = т 1 + т 2 + т 3 + т 4 . Через некоторое число циклов (примерно, через 5-10) происходило установление режима, то есть распределения параметров газа через временные промежутки т становились одинаковыми и не менялись от одного периода к другому. При этом выходной конец колонки был закрыт, открыт или на нем задавался какой-то закон изменения давления и расхода.

Для расчёта стационарно-периодических режимов работы колонки использовались уравнения движения газовой смеси через плотную упаковку микросфер [4, 5]. В настоящей статье уравнения не приводятся, поскольку авторы применяли их в работе [1], где привели к безразмерному виду, указали метод численного решения и провели проверку точности расчетов. Все действия с уравнениями здесь были бы аналогичными. Предполагалось, что микросферы изготовлены из кварцевого стекла. Численное решение уравнений осуществлялось методом Мак-Кормака, полунеявная версия которого описана в [6]. Ось x разбивалась на 200 равных отрезков, дальнейшее измельчение сетки не приводило к заметным изменениям результатов. В данном варианте выходной конец колонки был открыт и поддерживалось давление смеси 0,10 МПа. Радиус микросфер составлял 5 микрон, их толщина — 1 микрон. Доля заполнения колонки частицами равнялась 0,6; длина колонки — 10 м; временные параметры (в секундах) — т 1 = 10 , т ₂ = 5 , т 3 = 1 , т 4 = 5 . Таким образом, период процесса составлял 21 секунду. Исследовалось изменение во времени осевых распределений основных параметров газовой смеси: давления P ; скорости U ; коэффициента обогащения смеси гелием Г , определяемого формулой Г = ( р / P ₂)/(р / P ₂) in и характеризующего эффективность работы обогатительной установки. Индексы 1 и 2 обозначают гелий и метан соответственно, индекс in — исходное значение.

На рисунке 1 показаны графики распределения вдоль оси колонки давления смеси, обезразмеренного на величину максимального парциального давления метана на входе колонки, на рисунке 2 — соответствующие кривые для коэффициента обогащения смеси гелием Г . Расстояние x указано в безразмерных единицах (отнесено к длине колонки). Цифры обозначают времена, отсчитываемые от момента начала цикла и отвечающие началу отдельных стадий процесса (с): цифра 1 — t = 0; 2 — t = 10; 3 — t = 15; 4 — t = 16; 5 — t = 18,5. Из рисунка 2 видно, что в течение некоторого времени из колонки выходит смесь, обогащенная гелием.

Одной из основных целей работы являлся поиск таких способов изменения давления на концах колонки, при которых получаются наибольшие коэффициенты

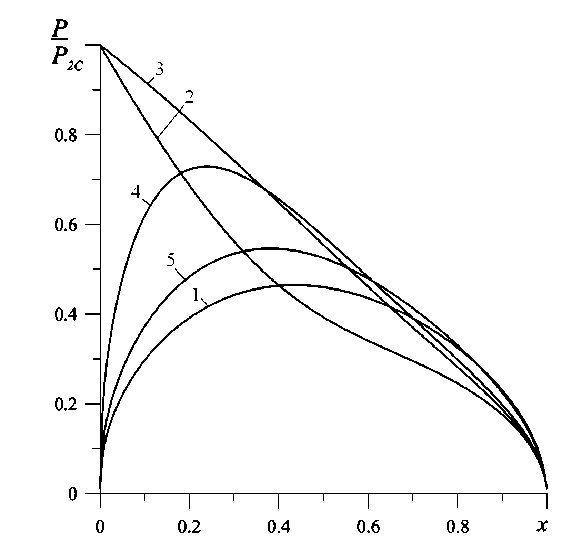
Рис. 1. Распределения давления смеси вдоль оси колонки для разных фаз цикла.

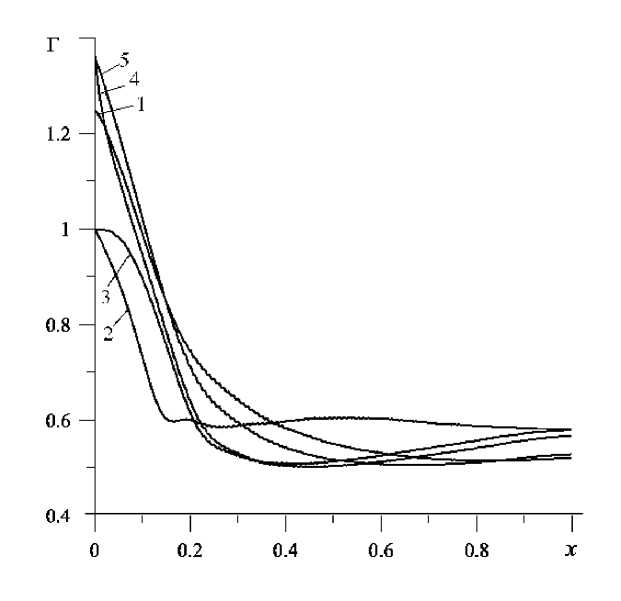
Рис. 2. Распределения вдоль оси колонки коэффициента обогащения гелием для разных фаз цикла.

обогащения смеси гелием. На рисунке 3 в качестве одного из примеров представлены графики распределения коэффициента обогащения смеси гелием при следующей организации процесса. При температуре 400ºК и исходном давлении смеси в колонке 0,1 МПа с закрытым выходным концом давление на входе линейно возрастало до 10 МПа в течение 1 с. После этого входное давление поддерживалось постоянным до того момента, пока давление на конце колонки не достигало 7 МПа. Это происходило в момент времени t = 32,2 с. После этого клапан на правом конце открывался и давление

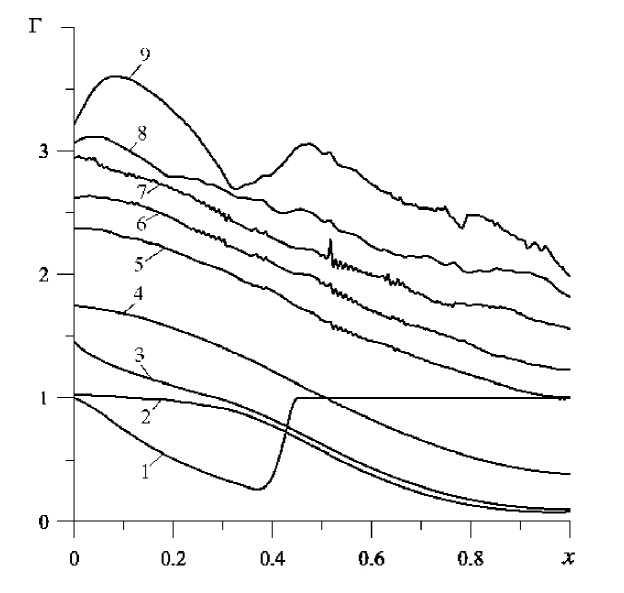
Рис. 3. Распределения вдоль оси колонки коэффициента обогащения гелием для одного из вариантов нестационарного процесса.

здесь поддерживалось постоянным и равным 7 МПа. При t =37,16 с вход в колонку закрывался (поступление смеси прекращалось), а давление на выходе сбрасывалось линейно за 1 с до значения 0,1 МПа. В момент t = 39,64 с давление на входе сбрасывалось за 1 с до 0,1 МПа и смесь выпускалась из обоих концов колонки. Цифры на графике соответствуют следующим моментам времени (с): 1 — 3,44; 2 — 39,6; 3 — 42,1; 4 — 64,4; 5 — 133,8; 6 — 173,4; 7 — 252,7; 8 — 332; 9 —406,3. График показывает, что возможно достижение достаточно высоких значений Γ , то есть смесь может обогащаться гелием в 3–4 раза (небольшие колебания связаны с погрешностями расчётов).

Таким образом, выполненные расчеты показывают, что путем подбора параметров процесса можно добиться существенного увеличения концентрации гелия в исходной смеси.

Представленная работа является частью интеграционного проекта СО РАН № 41 «Экспериментальное и теоретическое исследование диффузионно-сорбционных процессов с использованием полупроницаемых ценосфер».