Цикличность численности черношапочного сурка Marmota camtschatica Doppelmayeri в Баргузинском заповеднике

Описание цикличности численности животных можно встретить в литературе издавна [Воронин, 1978; Гниненко, Серый, 2003; Формозов, 1935; Шубина, 2010], однако этот феномен не становится центральным объектом изучения биологов. Такое отношение к цикличности не удивительно, ведь воспринимают это явление не как самостоятельное, что требует отдельного изучения. Обнаружив цикличность многолетней численности и примерно установив ее период, исследователь высказывает предположение о причинах этой цикличности. Мысль о том, что имеется определенная временная организация биологической системы (например, популяции), характеристикой которой является ее спектр периодов, встречается в небольшом количестве научных работ. Мы надеемся, что со временем специальные исследования в этой области будут накапливаться и появится возможность формулирования новых биологических закономерностей и углубленного понимания проблем динамики численности организмов.

В данной работе представлены результаты изучения цикличности численности черношапочного сурка ( Marmota camtschatica ) на нескольких учетных площадках Баргузинского заповедника. В задачи исследования входили оценка статистических характеристик многолетней численности этого вида; построение спектров колебаний численности его в разных поселениях; расчет характеристик гармонических составляющих этих спектров; построение прогнозной модели численности вида исходя из цикличности ее хода.

На Баргузинском хребте в 1997–2007 гг. отмечались стабильно высокая численность черношапочного сурка на учетных площадках и выровненная демографическая структура его популяции. С 2010 г. наблюдается значительное снижение численности семей, числа зверьков в семьях и доли молодых особей, а в ряде случаев и полное исчезновение колоний [Козулин и др., 2016].

Материал и методика его обработки

Учеты проводили в гольцовом поясе Баргузинского хребта на постоянных площадках площадью от 0,5 до 1,5 км2. В данной работе использованы сведения, полученные в результате учетов на трех площадках: в верховьях р. Шумилиха (N54,0623°, E109,6311°, h=1540–1650 м над ур.м.), на правом истоке р. Таркулик (N54,2995°, E109,9971°, h=1660–1685 м над ур.м.) и на ключе Жигуна (N54,3435°, E109,8547°, h=1500–1550 м над ур.м.). Ежегодно в конце июля — августе регистрировалась численность зверьков на учетной площадке, соотношение взрослых особей и сеголеток, соотношение полов.

Для числовой обработки эмпирических временных рядов с целью выявления в них скрытых периодических составляющих использовали следующие методы — непараметрический (преобразование Фурье) и параметрический (модифицированный метод наименьших квадратов Прони). Для выявления скрытых колебаний численности применяли быстрый анализ Фурье [Дженкинс, Ваттс, 1971]. Детальное описание таких методик расчета биологических ритмов дано А. А. Сорокиным [1981] и Л. Н. Ердаковым [1990]. Использование спектрального анализа, соответствующего модели временного ряда, способствует тому, что его результаты становятся информативными, то есть имеющими физическую интерпретацию. Эмпирически опре- 93

деляемыми параметрами были шаг суммирования, длина автокорреляционной функции, форма и ширина корреляционного окна. В итоге мы получали спектр, на котором происходит визуализация распределения функции спектральной плотности, в каждой точке его она соответствует средней мощности в полосе частот определенной ширины — «пик на спектре». Такой анализ давно и успешно применяется для определения популяционных циклов. Так, он был использован при описании колебаний численности морского котика [Колесник и др., 1978], определении цикличности в динамике численности обыкновенной полевки [Николов, 1981] и красно-серой полевки на о-ве Хоккайдо [Bjornstad et.al., 1996] . Его использовали для расчетов ритмов многих видов животных Печоро-Илычского заповедника [Бобрецов и др., 2000], оценки цикличности различных популяций грызунов Барабы [Ердаков, 2011] и изучения цикличности динамики лесных полевок [Ердаков, Моролдоев, 2017, 2018] .

Для оценивания цикличности применяли программы спектрального анализа, находящиеся в собственности ИСиЭЖ СО РАН. Оценка спектральной плотности мощности (СПМ) осуществлялась методом Уэлча [Марпл-мл., 1990]. Все расчеты выполнены с использованием свободной системы для математических вычислений GNU Octave. В частности, для оценивания СПМ методом Уэлча использовалась функция pwelch из пакета расширений Octave-Forge. Разработанный интерфейс позволил проводить обмен данными и всю обработку, включая выбор размера и количества окон, графическое представление данных и т. п. в диалоговом режиме.

Прогноз осуществлялся с помощью вычислительной программы для по-лигармонического анализа временных рядов. Эта методика позволила оценить степень колебательности ряда, выделить значимые по амплитуде гармоники и рассчитать их параметры. Основные принципы метода такого группового учета аргументов — разделение исходного ряда на обучающую и проверочную выборки и оценка качества модели по глубине минимума внешнего критерия на проверочной выборке. Выбор вида внешнего критерия является прерогативой исследователя и определяется целями моделирования [Кошулько, Попков, Юрачковский, 1987]. Наилучшую аппроксимацию эмпирической кривой дает модельная кривая, построенная с использованием максимального числа выделенных для процесса гармонических составляющих. Модифицированный метод наименьших квадратов Прони уместен и при небольших рядах, чаще всего затухающих колебаний, в последнее время все чаще используется для такого материала [Кухаренко, 2009]. Оба способа обработки временных рядов реализованы в авторской программе «Harms» А. В. Тарновского.

Для трендов проверяли гипотезу об отличии коэффициентов от нуля и рассчитывали коэффициент детерминации R2. Полученные значения отражаются в тексте только в том случае, когда нулевая гипотеза о равенстве обоих коэффициентов регрессии нулю отбрасывается. В противном случае линейная регрессия исключается из модели процесса.

Для статистической обработки использован пакет программ Past.

Результаты и их обсуждение

Статистические оценки численности черношапочного сурка

Средняя численность сурка в годы учета была статистически не различима в поселениях Шумилиха и Таркулик и достоверно ниже в поселении Жигун (табл. 1). В последнем наблюдалась повышенная вариабельность изменений плотности зверьков по годам; при средних оценках эти различия нивелировались. Однако если в больших (насыщенных зверьками) поселениях картина динамики численности сохранялась стационарной, то в поселении Жигун наблюдалось высокодостоверное снижение численности за сроки наблюдений. В средних данных по заповеднику этот отрицательный тренд численности сохранялся.

Таблица 1

Статистические показатели численности в поселениях черношапочного сурка

Учетная площадка	n	Численность, M±m	σ	CV, %	Тренд
Шумилиха	21	18,94±1,57	7,18	37,91	19,333 — 0,039 * t;α>0,05
Таркулик	21	18,67±2,06	9,45	50,62	24,550 — 0,588 * t; α>0,05
Жигун	21	8,41±1,66	7,61	90,49	16,972 — 0,856 * t; R2=0,486; α≤0,01
Средние	21	15,18±1,30	5,96	32,26	20,466 — 0,528 * t; R2 =0.303; α≤0,01

Примечание. n — число рассматриваемых лет, M — среднее, m — ошибка среднего, σ — квадратичное отклонение, CV — коэффициент вариации, R² — коэффициент детерминации.

Сравнение хронограмм хода численности в трех поселениях показало их заметную несогласованность (рис. 1). Различия можно заметить не только в хронограмме поселения Жигун, где численность очень низкая (рис. 1в), но и в поселениях, где численность статистически не различима по многолетней средней (рис. 1а, б). Общность наблюдается только в тенденции снижения численности в последние годы наблюдений. Несинхронность хода численности в трех поселениях подтверждается и статистически незначимыми коэффициентами ранговой корреляции Спирмена для поверки согласованности с нормальным распределением использованы расчеты p -значения по нескольким критериям. Наиболее показательно оно для критерия Шапиро-Уилкоксона, но учитывались p -значения и для других критериев (Монте-Карло, Харке-Бера). Оценки оказались слишком велики, чтобы говорить о нормальном распределении в выборках, поэтому воспользовались коэффициентом ранговой корреляции для выяснения синхронности хода численности в разных поселениях сурка.

Синхронным при высокой значимости оказался только ход средней численности со всеми поселениями (ƿ=0,67362–0,7362; α≤0,01), что можно объ- яснить тем, что все поселения имели различающийся ход численности за сроки наблюдений.

Спектральные оценки цикличности динамики численности черношапочного сурка

Построенные спектры колебаний многолетней численности для каждого поселения позволили установить сходные для них гармонические составляющие, а также выявить различия в гармониках. Для всех поселений обычна 2-2,5-летняя цикличность, причем самая мощная цикличность наблюдалась в поселении Шумилиха (рис. 2а), а почти не проявлена в поселении Жигун (рис. 2в). Также в зоне высоких частот доминирует в поселении Жигун 3-4летний цикл, отмеченный и в поселении Шумилиха. В низких частотах сходство циклов во всех поселениях не наблюдается.

Таким образом, при визуальной оценке спектров колебаний численности можно заметить некоторую общность их в полосах высоких частот и совершенное разнообразие в средних и низких частотах. Добавляет различия в картинах спектров и несоответствие мощностей даже в близких по периоду гармонических составляющих.

Более точно сравнить спектральные характеристики можно по оценкам их параметров (табл. 2). Обращает на себя внимание близость спектров в поселениях Шумилиха и Таркулик. В трех основных полосах частот, по-видимому, характерных для цикличности этого вида, наблюдается полное сходство (≈10-, 5- и 2,5-летние колебания). По соотношению мощностей периодических составляющих здесь также наблюдается подобие. Заметно отличается набор ритмов численности в поселении Жигун, где основная мощность сосредоточивается в высоких частотах, а самих гармоник на спектре оказывается вдвое меньше, чем в других поселениях. Можно предположить, что такие заметные различия в цикличности вызваны особенностями местообитаний у этих поселений.

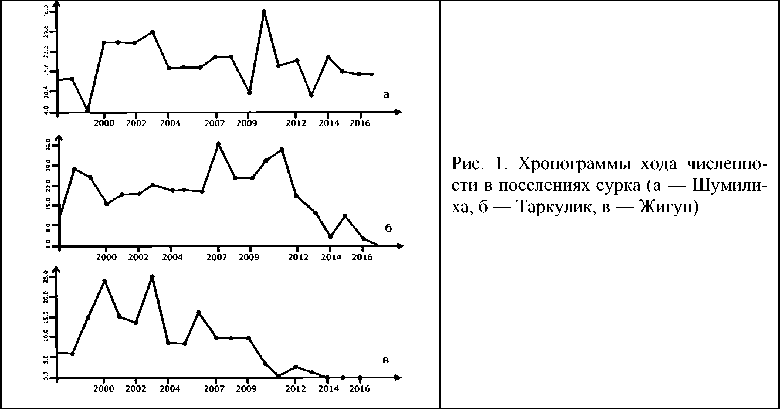
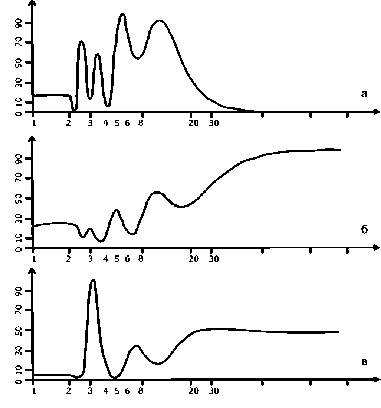
Рис. 2. Спектры цикличности многолетней численности в поселениях сурка

(а — Шумилиха, б — Таркулик, в — Жигун). По оси абсцисс указаны периоды (лет), по оси ординат — мощность (в%)

Таблица 2

Соотношение величины и мощности периодических составляющих черношапочного сурка

Период, лет Учетная площадка	15–20	10–14	7–9,5	4,5–6	3,5–4,4	2,0–2,7
Шумилиха		11.0 2,17		5.5 2,25	3.4 1,76	2.5 1,95
Таркулик		10,0 2,41		4,7 1,98		2,8 1,38	2,1 1,50
Жигун			7,0 1,39		3,1 2,35
Средние значения	19,7 2,05		8,2 1,71	5,1 0,91	3,5 1,41	2,8 0,48	2,4 0,91

Оценка вероятных изменений численности черношапочного сурка в ближайшие годы

Результаты многолетних учетов сурка показывают, что относительно небольшая численность этого вида подвержена сильным ежегодным изменениям (рис. 3). Подъемы ее обычно имеют цикличность в три и шесть лет. В последние годы численность этого вида стабильно малая, что и определило достоверный отрицательный тренд численности.

Используя информацию об основных циклах динамики, можно построить модель [Кошулько, Попков, Юрачковский, 1987], аппроксимирующую эмпирическую кривую динамики численности (рис. 3).

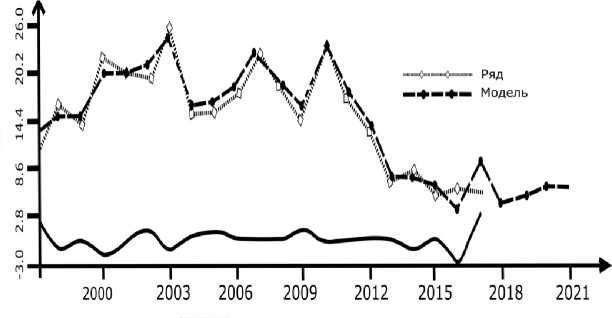
Рис. 3. Аппроксимация хода численности сурка модельной кривой (участок с 2017 по 2021 г. — прогноз, на оси ординат — число особей, графики исходного ряда, модели и «шума»)

Полагая, что причины, воздействующие на динамику (внешние и внутренние), постоянно проявляют себя, мы можем продолжить кривую численности во времени. Поведение модельной кривой позволило ожидать определенных изменений численности в ближайшие пять лет. По этому прогнозу популяция сурка снизится в 2018 г., достигнув плотности в 4,54 особи, далее к 2021 г. будет наблюдаться небольшой плавный ее подъем до ≈6-6,5 особей. Наблюдающаяся низкая численность начиная с 2013 г., вероятно, является частью большого, примерно 20-летнего цикла (табл. 3), поэтому большой подъем численности следует ожидать только через 10–15 лет.

Таблица 3

Параметры полигармонического модельного ряда для хода численности черношапочного сурка

N	F	T	Ph	U	dQ	Q
1	0,044	22,564	9,859	4,962	54,66	54,66
2	0,115	8,665	4,253	2,752	17,53	72,19
3	0,422	2,369	1,033	1,871	7,40	79,59
4	0,282	3,540	-0,852	2,164	6,90	86,49
5	0,218	4,579	0,394	1,716	6,39	92,87

Примечание. N — номер цикла; F — частота; T — период; Ph — фаза; U — амплитуда; dQ — дисперсия; Q — накопленная дисперсия.

Заключение. Таким образом, многолетний ход численности сурка не синхронен в разных его поселениях, в большинстве учетных площадок он стационарен, а в малочисленных поселениях наблюдается заметный отрицательный тренд. Многолетние изменения численности черношапочного сурка цикличны. Для них характерны колебания в трех полосах частот: ≈10-, 5- и 2,5-летних; наибольшей мощностью обладают обычно низкочастотные циклы.

Различия в спектрах цикличности численности сурка, видимо, связаны с особенностями природно-климатического фона в его поселениях. Прогноз численности возможен с использованием сведений о его цикличности при помощи модели, основанной на модифицированном методе наименьших квадратов Прони.

Исследование поддержано Российским фондом фундаментальных исследований (проект № 17-04-00269) и Программой фундаментальных научных исследований (ФНИ) государственных академий наук на 2013–2020 гг., проект № VI.51.1.9 (АААА-А16-116121410119-4).