Cлабая непрерывность оператора суперпозиции в пространствах последовательностей

При исследовании разрешимости операторных уравнений в банаховых пространствах важную роль играет принцип неподвижной точки Шаудера — Тихонова. Он утверждает, что в локально-выпуклом пространстве непрерывное отображение выпуклого компакта в себя обладает неподвижной точкой. Кроме метрической топологии на банаховом пространстве могут быть определены другие локально-выпуклые топологии, важнейшей из которых является слабая топология. Более того, ослабление топологии приводит к увеличению числа компактных множеств, и, следовательно, расширяются возможности применимости самого принципа Шаудера — Тихонова.

Таким образом, возникает необходимость изучения условий, как необходимых, так и достаточных, слабой непрерывности заданного отображения, действующего в некотором банаховом пространстве Z . Поскольку для линейного оператора ответ хорошо известен, а именно, линейный оператор T , действующий в банаховом пространстве Z, является слабо непрерывным в том и только том случае, когда T является непрерывным в метрической топологии, интерес представляет лишь изучение нелинейных операторов.

Один из важнейших классов нелинейных операторов — это класс операторов суперпозиции. Изучению условий слабой непрерывности оператора суперпозиции в пространствах последовательностей и посвящена настоящая работа. Так, в первой части даны необходимые в дальнейшем определения и результаты, относящиеся к теории оператора суперпозиции или к пространствам последовательностей. Вторая и третья части посвящены, соответственно, необходимым и достаточным условиям слабой непрерывности оператора суперпозиции.

Используемые ниже определения, обозначения и факты, относящиеся к идеальным пространствам, в частности к пространствам последовательностей, взяты из [4] (см. также [5]), а к оператору суперпозиции из [7].

Некоторые определения, обозначения и вспомогательные результаты

Пусть (Q, A , ^ ) — пространство с ^-конечной, неотрицательной мерой ^. Напомним, что измеримое множество A, ^(A) > 0, называется атомом [3, с. 82], если для любого измеримого множества B , B С A, либо ^(B) = 0, либо ^(B ) = ^(A). Множество Q может быть разбито [3, с. 83-84; 7, с. 8] на два непересекающихся измеримых множества Q c и Q d , причем на Q c мера ^ непрерывная, т. е. всякое измеримое множество B С Q c может быть представлено в виде B = Bi t B 2 , ^(Bi) = ц(В2) = 2 ц(В ), а на Q d мера ^ дискретная, т. е. Q d представимо в виде объединения не более, чем счетного числа атомов.

Через L o (Q, ^) обозначается пространство, состоящее из эквивалентных классов ^-измеримых на Q функций. Линейное подпространство X пространства L o (Q,^) называется идеальным [4], если X является банаховым пространством и соотношения | y | 6 | x | , x G X, y G L o (Q,^) влекут y G X (т. е. X — порядковый идеал в L o (Q, ^)) и \\ y \\ 6 ||х Н -Всякое идеальное пространство является банаховой решеткой. Для произвольного измеримого множества A, через P A обозначается порядковый проектор, определенный по правилу P a x = X A X, x G L o (Q, ^). В зависимости от необходимости P a может рассматриваться действующим, как в X, так и в L o (Q,^).

Пусть функция f действует из Q х R в R. Говорят, что f определяет оператор суперпозиции f [7, с. 10], действующий в идеальном пространстве X, если оператор ( f x)(s) = f (s,x(s)) отображает X в X. При этом, всякая функция f : R ^ R может рассматриваться, как функция из Q х R в R, а значит и определять оператор суперпозиции f по правилу ( f x)(s) = f (x(s)). В общем случае, оператор f может даже не действовать в L o (Q,^), т. е. отображать измеримые функции в измеримые. Говорят, что функция f удовлетворяет условию Каратеодори [7, с. 16], если для почти всех s функция f (s, • ) непрерывная и для всех и функция f ( • , и) измеримая. Если f удовлетворяет условию Каратеодори, то оператор f действует в L o (Q,^).

В дальнейшем, под непрерывным отображением одного топологического пространства в другое понимается отображение, при котором прообраз каждого открытого множества открыт; это также равносильно тому, что каждая сходящаяся обобщенная последовательность отображается в сходящуюся. Если отображение переводит каждую сходящуюся последовательность в сходящуюся последовательность, то оно называется секвенциально непрерывным . Очевидно, всякое непрерывное отображение является секвенциально непрерывным.

Напомним, что для банахова пространства Z слабая топология a(Z, Z * ) на Z — это локально-выпуклая топология, порожденная следующим базисом окрестностей

O(x; z*,..., z* е) = {z : |z*z — z*x\ < e, i = !,•••, k}, где элемент x G Z, функционалы z* G Z*, число e > 0. Слабая непрерывность оператора T : Z ^ Z означает непрерывность T, как отображения пространства Z со слабой топологией в себя.

Пусть X — идеальное пространство, оператор суперпозиции f действует в X . Обозначим через C X носитель X [5, с. 59], т. е. наименьшее по включению (с точностью до множества нулевой меры) измеримое множество вне которого почти всюду равна нулю любая функция x G X. Тогда P q \ c _x ( f x) = 0 для всех x G X. Если теперь рассмотреть пространство X, как идеальное пространство на C X (будем обозначать его через X 0 ), а через f X обозначить сужение f на C X × R, то оператор суперпозиции f X , определенный по f X , будет действовать в X 0 и являться слабо непрерывным тогда и только тогда, когда слабо непрерывным является f . Следовательно, в дальнейшем считаем C x = Q.

Это равносильно [5, с. 195] существованию в X функции положительной почти всюду на Q; такие функции называются слабыми единицами. При этом, если A — атом меры µ, то χ A ∈ X.

Функция g : R ^ R представимая в виде g(u) = a + bu, где а и b — некоторые действительные числа, называется аффинной . Аналогично, оператор T , действующий в идеальном пространстве X , называется аффинным , если для любого элемента x ∈ X справедливо равенство Tx = а + bx в X, где функции a,b : Q ^ R. Ясно, что аффинный оператор T является оператором суперпозиции, определяемый функцией f (s,u) = a o (s) + b o (s)u, где a 0 и b 0 — произвольные представители класса эквивалентности a и b , соответственно. Пусть теперь некоторый оператор суперпозиции f : X ^ X является аффинным, т. е. f x = a+bx. Взяв x = 0 получаем а = f 0 = f (s, 0). Поскольку C x = Q, существует [5, с. 58, ∞

60] последовательность измеримых множеств A i таких, что A i С A 2 С ..., |J A i = Q и i =1

X A i Е X для всех i. Тогда для почти всех s Е A i имеем f (s, 1) = ( f X A i )(s) = f (s, 0) + b(s), откуда b(s) = f (s, 1) — f (s, 0) для почти всех s Е Q. Кроме того, функции а и b измеримы. Далее, если f удовлетворяет условию Каратеодори, то оператор суперпозиции f : X ^ X аффинный в том и только том случае, когда для почти всех s функция f (s, • ) аффинная. В пояснении нуждается лишь необходимость, и именно она использует условие Каратеодори. Пусть f x = а + bx. Если A — измеримое множество, X A Е X, то для рационального числа u и для почти всех s Е A имеем f (s,u) = f ( ux a )( s ) = a(s) + b(s)u. Следовательно, равенство f (s, u) = a(s) + b(s)u справедливо для почти всех s Е A и u Е R. Как и выше, используя соотношение C x = Q, получаем требуемое.

Как показано в [1] слабая непрерывность оператора суперпозиции f , действующего в идеальном пространстве X с непрерывной мерой и определяемого функцией f , удовлетворяющей условию Каратеодори, равносильна его аффинности.

С другой стороны, оператор суперпозиции f , действующий в пространстве L _∞ с произвольной мерой и задаваемый функцией f , удовлетворяющей условию Каратеодори, является [2] слабо секвенциально непрерывным в том и только том случае, когда f задает непрерывную по u кривую в L ∞ , т. е. когда из сходимости u n → u 0 следует сходимость f (>u n ) ^ f (>u o ) в L ^ . Значит, всякая непрерывная функция f : R ^ R определяет слабо секвенциально непрерывный оператор суперпозиции f в L ∞ ; в частности, слабо секвенциально непрерывными в L ^ являются операторы f x = | x | и f x = x². Впрочем, слабая секвенциальная непрерывность первого из них может быть получена и как следствие слабой секвенциальной непрерывности решеточных операций в AM -пространстве [8, с. 106]. Из приведенных примеров видна разница между слабой непрерывностью и слабой секвенциальной непрерывностью. Еще раз подчеркнем, что ниже будет изучаться слабая непрерывность, и именно она, а не слабая секвенциальная непрерывность требуется в различных теоремах, связанных с неподвижными точками, в частности, в теореме Шаудера — Тихонова.

Ясно, что оператор суперпозиции f , действующий в некотором идеальном пространстве X , является слабо непрерывным тогда и только тогда, когда слабо непрерывным будет оператор gx = fx — f0. Оператор g также представляет собой оператор суперпозиции, определяемый функцией g(s,u) = f (s,u) — f (s, 0), причем g(s, 0) = 0, а значит g0 = 0. В связи с этим, в дальнейшем, если не оговорено противное, мы будем предполагать f0 = 0. Тогда, очевидно, выполняется следующее свойство дизъюнктной аддитивности: если x ± у в X, то f(x + y) = fx + fy. При этом fx ± fy. На самом деле, supp fx С supp x, а значит компонента Bfx , порожденная fx в X , содержится в компоненте Bx , порожденной x в X. Если A — атом меры ^, то BXA = {Axa : ^ Е R}. Тогда для u Е R имеем f (uxa) = Aa,uxa, где Aa,u G R. Определим функцию Ja(u) = AA,U. Для почти всех s € A справедливо равенство f (s,u) = fA(u).

Если Q состоит из конечного числа различных атомов Ai, i = 1,k, то, очевидно, всякое идеальное пространство X на Q является конечномерным. Следовательно, слабая непрерывность в X равносильна непрерывности в метрической топологии. Пусть оператор суперпозиции f действует в X. Тогда, если x = Pk=1 aiXAi, то fx = f

(X i=1

a i χ A i

kk

= 52 ^f (a i X A i ) = 52 f A i ⁽a i )X A i • i =i               i =i

Отсюда легко видеть, что, в данном случае, оператор суперпозиции f является слабо непрерывным в том и только том случае, когда непрерывны функции fAi . В частности, это верно, когда функция f удовлетворяет условию Каратеодори; но не наоборот. В связи с этим, в дальнейшем мы будем рассматривать лишь бесконечномерные идеальные пространства на множестве с дискретной мерой, т. е. случай, когда Q состоит из счетного числа атомов.

Всякое идеальное пространство X на множестве с дискретной мерой линейно изомет-рично и порядково изоморфно идеальному пространству X ∞ на множестве натуральных ∞

чисел N со «считающей» мерой. Действительно, если Q = | | A i , где A i — атомы, то опре- i =i

делим

X ∞

x

∞

= (x ₁ ,x ₂ ,...) : ряд 52 x i X A i сходится в X по порядку i =i

I

и положим ||x|| x ^ = ||о- Е£1 X i X A i k x , где символ о означает порядковую сходимость ряда или последовательности. Теперь требуемый изоморфизм Ф : X ^ ^ X определяется, как Ф(Х 1 ,Х 2 ,...) = о -PS i. X i X A i .

Пусть f — оператор суперпозиции, действующий в X. Тогда, если x = о - y^i X i X A i , то f x = о -^ i =i f (x i X A i ). В самом деле,

∞ f (о -52 XiXAi)

i = n +1

∞ f (o - 52 XiXAi) + f (xn+1XAn+i )

i = n +2

∞

^{f (o} -52 ^x i X A i ) i = n +2

⁺ |^{f (x} n +1 X A n+i ) ^|

>

∞

^{f (o} -52 ^x i X A i ) i = n +2

Следовательно, последовательность |f (o-E i = n +1 x i X A i ) | убывает по n. Отсюда, учитывая соотношение x A j ± f (о-E£ _n+1 x i X A i ) при j = 1,n, имеем | f (о-E£ _n+1 x i X A i ) | I 0. Последнее соотношение вместе с равенством f x — f (^2П =₁ x i X A i ) = f (о -^ i = n +₁ x i X A i ) дают P n =1 ^{f ( x} i X A i ) = ^{f (}P n =1 ^x i X A i ) ^{— f x}.

Определим оператор f ^ , действующий в X ^ , по правилу f ^ = Ф ^{- 1} f Ф. Для элемента x ^ = (x ₁ ,x ₂ ,...) G X ^ имеем

∞ f^x^ = Ф-1 f I о-52 xiXAi I i=1

= Ф ^{- 1}

∞ о-X i=1

^{f ( x} i X A i )

= Ф ^{- 1}

∞ о-X i=1

^f A i ^{( x} i )X A i

= (f A i (x 1 ),f A ₂ (x 2 ), . . .),

следовательно ( f ^ x ^ ) i = f A i (x i ), а значит оператор f ^ является оператором суперпозиции, определяемый функцией f ^ (n, u) = f A n (u). Очевидно, f ^ является слабо непрерывным в том и только том случае, когда слабо непрерывным является f . Таким образом, в дальнейшем, без ограничения общности, мы будем предполагать все рассматриваемые идеальные пространства определенными на множестве натуральных чисел N со «считающей» мерой. Ниже такие пространства будут просто называться пространствами последовательностей.

Пусть X — пространство последовательностей. Двойственное к X пространство X ⁰ [4] определяется как

X ⁰

=

ОО

= ⁽z i ,z 2 ,...^{) :} ^2

i =1

x i z i <  го для всех x = (x 1 ,x ₂ ,...) G X

Каждой последовательности z G X ⁰ можно поставить в соответствие функционал z * G X * по правилу z * x = ^2i=i z i x i , при этом, в силу теоремы Лозановского [5, с. 198], z * будет принадлежать компоненте порядково непрерывных функционалов на X, т. е. z * G X ~ . Наоборот, всякий функционал z * G X ^ может быть представлен в таком виде, где z G X ⁰ . С нормой ||z k x o : = k z * k x * пространство X ⁰ будет являться пространством последовательностей. Таким образом, X ⁰ может быть отождествлено с X ~ . Тогда пространство X * , сопряженное к пространству X, является банаховой решеткой, представимой в виде суммы двух дизъюнктных компонент X * = X ⁰ ® X s , где X s — пространство антинормальных функционалов [4]

X s = { x * G X * : | x * | x = 0 для некоторой слабой единицы x G X } .

Например,

= ' i , ' ^ = { x * G С : x * (c o ) = { 0 }} .

Для пространств c o , ' p , 1 6 p <  го , двойственное совпадает с сопряженным.

Обозначим через e _n последовательность, в которой элемент с n-ым номером равен единице, а все остальные нулю. Правильной частью X ° [4] пространства X называется замыкание в X линейной оболочки элементов e _n . Справедливо равенство

X ^° = { x G X : x ^* x = 0 для всех x ^* G X ^s } .

Иными словами, X ° — это аннулятор X s .

Функция f : N х R ^ R удовлетворяет условию Каратеодори в том и только том случае, когда для всех n функция f (n, •) непрерывная. Аффинность оператора суперпозиции f , действующего в пространстве последовательностей X , будет равносильна аффинности функции f (n, •) для всех n. Пусть оператор суперпозиции f : X ^ X является слабо непрерывным, f0 = 0. Фиксируем n. Если последовательность действительных чисел uk → u, то uken → uen в X, а значит f (n, uk)en = f(uken) ^X^ ) f(uen) = f (n,u)en, откуда lim f (n, uk) = f (n, u). Следовательно, функция f (n, •) непрерывная, а значит k ^^

f удовлетворяет условию Каратеодори. Таким образом, условие Каратеодори оказывается необходимым для слабой секвенциальной непрерывности, а значит и для слабой непрерывности f . В дальнейшем, если не оговорено противное, мы считаем функцию f , определяющую рассматриваемый оператор суперпозиции f , удовлетворяющей условию Каратеодори.

В [6] изучалась слабая непрерывность оператора суперпозиции f в пространстве ' _го . Так, там было показано, что если функция f : R ^ R, то слабая непрерывность f в ' _го равносильна аффинности f . Найден класс слабо непрерывных в ' _го операторов суперпозиции «значительно» более широкий, чем класс аффинных операторов.

Ниже будет найден целый класс пространств последовательностей (теорема 1), в которых слабая непрерывность оператора суперпозиции f , определяемого функцией f : R ^ R, равносильна аффинности f . Не все пространства последовательностей удовлетворяют этому свойству, например, это не верно для Со (см. теорему 6 и следствие 7). Тем не менее, ниже будет показано, что в произвольном пространстве последовательностей X всегда можно построить слабо непрерывный оператор суперпозиции f не являющийся аффинным (см. следствие 10).

Необходимые условия слабой непрерывности

Следующая теорема выделяет класс пространств, в которых слабая непрерывность оператора суперпозиции f , определяемого функцией f : R ^ R, равносильна аффинности f .

Теорема 1. Пусть для пространства последовательностей X выполняются условия X 0 С С о и X 0 С ' _го (оба в теоретико-множественном смысле). Тогда оператор суперпозиции f , определяемый функцией f : R ^ R, слабо непрерывный в X в том и только том случае, когда f аффинная.

C В доказательстве нуждается лишь необходимость. Считаем f (0) = 0, а значит f0 = 0. Фиксируем ненулевые a, b Е R и е > 0. В пространстве X0 найдется неотрицательная последовательность x* = (xi, Х2,...) / со. Можно считать, что для некоторой подпоследовательности xnk будет xnk = 1                                              (*)

при всех k. В силу слабой непрерывности f в нуле, найдется a(X, X * )-окрестность O (0; x * ,..., x m , 5), для которой

f (O (0; x i ,..., x m , 5)) С O (0; x * ,e).                             ( ** )

Раскладывая каждый функционал x * на сумму x * = x * i + x * 2 , где x * i Е X ⁰ , x * 2 Е X s , и учитывая включение

O ⁽⁰; ^x * i ,..., x m i , ^x i2 ,..., x m 2 ,⁵/2) c O ⁽⁰; x i ,..., x m ,⁵⁾

можно считать x i ,..., x m 0 Е X ⁰ и x m _{o +}i ,..., x m Е X s для некоторого mo. Воспользовавшись включением X ⁰ С ' _го и при необходимости перейдя к подпоследовательности будем также предполагать существование пределов lim (x * ) n _k , i = 1,m o . Найдем индекс k →∞ k o , для которого

2 T b | ’

|(xi Kk0 — (xi Kk0+2 I < 2|0|, |(xi Kk0+1 — (xi )nk0+2 I < при i = 1, mo. Тогда последовательность

°enk0 + benk0+i — (°+b)enk0+2 е O(0; xi, •••, xm,5), следовательно, учитывая (∗) и (∗∗), e > |x*f(aenk0 + benk0+i — (a + b)enk0 + 2 ) 1

= | x * f (ae n k₀ ) + x * f (be n k₀+i ) + x * f ( - (a + b)e n k₀+2 ) | = | f (a) + f (b) + f ( - (a + b)) | .

В силу произвольности е получаем f (a) + f (b) + f ( — (a + b)) = 0. Устремив b к нулю имеем f ( — a) = — f (a), а значит f (a) + f (b) = f (a + b) для всех a,b E R. Следовательно, f (na) = nf (a) для n E N, откуда

/ n ^/ \        / 1 \    n ^/ , / 1 \    n ⁰

fin /a) = nfin //a) = n / ⁿ fin //a) = n / f^(a)

при n ^/ , n " E N. Таким образом, для произвольного рационального q и действительного a будет f (qa) = qf (a). В силу непрерывности f , последнее равенство справедливо для всех q E R. В итоге, f (u) = uf (1). Мы получили линейность f .

В общем случае, когда f (0) = 0, рассмотрим функцию g(u) = f (u) — f (0). Она порождает оператор суперпозиции g , действующий в X и являющийся слабо непрерывным. Поскольку g(0) = 0, по доказанному выше имеем g(u) = ug(1), откуда f (u) = f (0) + (f(1) — f (0))u. Таким образом, f — аффинная функция. B

Следствие 2. Пусть функция f : R ^ R определяет оператор суперпозиции f , действующий в пространстве ' 1 . Тогда f слабо непрерывный тогда и только тогда, когда f аффинная.

Условия на функцию f : N х R ^ R гарантирующие, что оператор f действует в ' 1 , имеются в [7, с. 94–95].

Решеточные операции |x|, x+, x , определенные на произвольном идеальном пространстве X , представляют собой важнейшие примеры оператора суперпозиции. Слабая непрерывность одной из этих операций равносильна слабой непрерывности любой из |x|+x           |x|-x двух оставшихся. Это сразу следует из равенств x = x+ — x , x+ =  —, x =  —. Тем не менее, их слабая непрерывность эквивалентна конечномерности данного пространства. Справедливость данного утверждения отмечалась в [8, упр. II.28(c), с. 152]. Для полноты мы приведем схему доказательства.

Лемма 3. Пусть E — нормированное пространство Рисса. Тогда решеточные операции слабо непрерывны в нуле в том и только том случае, когда пространство E является конечномерным.

C В доказательстве нуждается лишь необходимость. Фиксируем ненулевой функционал x * E (E * ) + . Нулевая точка является a(E, E * )-внутренней точкой поляры

[ — x * ,x * ] ° = { x : | z * x | 6 1 при | z * | 6 x * }

R                              ^(E,E*) n i i ^(E,E*) n относительно дуальной пары hE,E /. В самом деле, если xa —»  0, то |xa| —»  0, а значит существует индекс ag такой, что для любого z* E [—x*,x*] имеем |z*xa| 6 1 при a > ag, откуда xa E [—x*,x*]°. Для некоторых x*,...,xk E E* справедливо U := O(0;x*,...,xk, 1) C [—x*,x*]°, следовательно

[ — x * ,x * ] = [ — x * ,x * ] °° C U ° C Lin { x * ,..., x k } .

Таким образом, в банаховой решетке E * всякий порядковый интервал содержится в конечномерном пространстве, откуда dim E * <  го . Значит, dim E <  го . B

Лемма 4. Пусть функция f : N х R ^ R. Тогда f определяет оператор суперпозиции f , действующий в пространстве c g , в том и только том случае, когда для любого е > 0 существуют число 5 >  0 и натуральное N такие, что для всех n > N, | u | 6 6 имеет место неравенство | f (n, u) | 6 е.

В частности, f : R ^ R определяет оператор суперпозиции f , действующий в Со, в том и только том случае, когда f (0) = 0 и f непрерывна в нуле.

C Необходимость. Пусть оператор f действует в С о . В предположении противного, найдем подпоследовательность натуральных чисел n i и последовательность u i , lim u i = i →∞

0, для которых | f (n i ,u i ) | > е >  0. Последовательность x = (xi, Х2,...) определим, как x n i = U i и X j = 0, если j / { n i , П 2 ,... } . Тогда x G С о , а значит f x 6 С о . С другой стороны, | ( f x) n i | = | f (n i ,x n i ) | = | f(n i , u i ) | > е, мы пришли к противоречию.

Достаточность. Пусть элемент x G С о . Если f x / С о , то существует подпоследовательность натуральных чисел n i , для которой 0 < е <  | ( f x) _n i | = | f (n i ,x n i ) | , что невозможно при больших i, поскольку lim x i = 0.

i →∞

В случае f : R ^ R в пояснении нуждается лишь необходимость. Очевидно, f 0 G С о , а значит, поскольку f 0 = (f(0),f(0),...), имеет место равенство f (0) = 0. Для е > 0 существует 5 > 0 такое, что при больших n справедливы соотношения е >  | f (n, u) | = | f (u) | для | u | 6 5. Иными словами, f непрерывна в нуле. B

Лемма 5. Пусть функция f : R ^ R выпуклая, положительный функционал z * G ' i , k z * k = 1. Тогда для x G С о имеет место неравенство f (z * | x | ) 6 z * ( f | x | ).

C Пусть z * = (z i , Z 2 ,...) >  0. Прежде всего заметим, что в силу непрерывности выпуклой функции f , последовательность f | x | ограничена, а значит ряд ^^i zif ( | x i | ) = z * ( f | x | ) сходится. В силу равенства 53i =i z i = 1 найдется то, для которого £i = 0 i z i >  0. Тогда для т > то имеем

f

m

X j=1

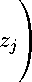
- 1

m zi|xi| i=1

=f

m

E^^^i|

, i=i £ zj j=1

m

6Е m^ f (N) = i=i     zj j=1

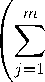
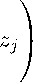
E z i ^{f (|x} i ^|)- i =1

- 1

m

Устремив m к бесконечности получаем f (z*|x|)= f

∞

E *| i=1

∞

6 X²- f(N) = z * ( f | x | ).

i =1

B

Напомним, что функция f : R ^ R называется функцией Орлича [7, с. 119, 137], если f неотрицательная, выпуклая, четная и f (0) = 0.

Теорема 6. Пусть функция f : R ^ R является функцией Орлича, причем f (u) > 0 при всех u = 0. Тогда оператор суперпозиции f , действующий в С о , не является слабо непрерывным в нуле.

C В силу леммы 4 оператор f действует в Со. Фиксируем положительный функционал z* = (zi,z2,...) G со = 'i, kz*|| = 1, и число е > 0. Найдется 5 > 0, для которого неравенство f (a) < 5 влечет |a| < е. Предположим противное, т. е. что оператор f слабо непрерывен в нуле. Тогда для некоторой ст(со,'1)-окрестности U нуля справедливо включение f (U) С O(0; z* ,5). В силу леммы 5 для произвольного x G U справедливо неравенство f (z*|x|) 6 z*(f|x|). Поскольку f четная f|x| = fx, а значит f (z*|x|) < 5, откуда z∗ |x| < ² для всех x ∈ U. Мы получили слабую непрерывность решеточных операций в нуле. В силу леммы 3 это невозможно. B

Следствие 7. Каждая из функций | u | p , (1 + | u | p ) q — 1, где p,q >  1, e ^{| u |} — 1, определяет оператор суперпозиции, действующий в пространстве c g и не являющийся слабо непрерывным в нуле.

Следующая теорема дает условия, при которых функция f : N х R ^ R определяет оператор суперпозиции f , не являющийся слабо непрерывным. Пространство последовательностей X назовем инвариантным относительно растяжения, если для любой последовательности z = (z i , z ₂ ,...) G X и подпоследовательности натуральных чисел n k последовательность х, определяемая, как х _{П к} = z k и X i = 0 при i / { n i ,n 2 ,... } , также принадлежит пространству X. Пространства c g , ' p , 1 6 p 6 го , являются инвариантными относительно растяжения.

Теорема 8. Пусть неотрицательная функция f : N х R ^ R определяет оператор суперпозиции f, действующий в пространстве последовательностей X, причем двойственное к X пространство X0 является инвариантным относительно растяжения и для всех k∈N sup f (n,u) = +го.                                 (*)

n > k,u ∈ R

Тогда f не является слабо непрерывным ни в одной точке пространства X .

• <1 Фиксируем слабую единицу z = (z i ,z 2 ,...) G X 0 . Найдем последовательность U k G R и подпоследовательность натуральных чисел n k , для которых f(n k , U k ) >  k при всех к. Определим последовательность z 0 , как z n k = z k и z i = 0 при i / { n, n _{2 )}... } . Тогда z ⁰ ∈ X ⁰ . Рассмотрим произвольный элемент x ∈ X и покажем, что оператор f не является слабо непрерывным в х. В предположении противного найдется a(X, X * )-окрестность U : = O (х; х * ,..., x* m , 5) точки х, для которой f (U) С O ( f х; z ⁰ ,1). Существует m

элемент y G П N (х * ), где N (х * ) — ядра функционалов х * , такой, что носитель supp у — i =1

бесконечное подмножество множества {ni,n2)...}. Для некоторого kg G N, удовлетворяющего неравенству kg > 1 + |z0fх|, будет yn = 0. Положим А = —---—. Поскольку k0                                   ynk0

х + Ау G U имеем

∞

1 >  | z ⁰ f (х + Ау) — z'f х | >  X z n f (n, х п + Ay n ) — | z 0 f х | n =1

• > ^z n k₀ ^f(n k 0 ^,х П к₀ ^{+ А}У п к₀ ) ^{— |z} 0 ^{f х|} = ^z k 0 ^f(n k 0 ^,U k 0 ) ^{— |z} 0 ^{f х|} >  k g ^{— |z} 0 ^{f х|} >  1,

мы пришли к противоречию. B

Для случая пространства ` _∞ результат аналогичный предыдущей теореме ранее был получен в [6].

Достаточные условия слабой непрерывности

Следующая теорема для произвольного пространства последовательностей X выделяет широкий класс функций, определяющих слабо непрерывный оператор суперпозиции в X. Ниже через C b (R) обозначается пространство ограниченных непрерывных функций на R с нормой k g k c b ( R ) = sup | g(u) | .

u ∈ R

Теорема 9. Пусть функция f : N х R ^ R определяет оператор суперпозиции f , действующий в пространстве последовательностей X , причем выполнены следующие условия :

• (a)    Функция f удовлетворяет условию Каратеодори ;

• (b)    Имеет место включение f (X) С X ° ;

• (c)    Существует индекс n g G N такой, что для всех n >  n g функции f (n, • ) ограничены, и, кроме того, последовательность

£,...,0, k f ⁽n g , • ⁾ k c b ( R ) , k f ⁽n g + 1, • ⁾ k C b ( R ) , . . . ^G X "•

( * )

• ¹    z }                                             I

  n o - 1

  
  

Тогда оператор суперпозиции f является слабо непрерывным в X .

C Фиксируем последовательность x = (x i ,X 2 ,••• ) G X. Для произвольных функционала z * G X ^s и элемента z G X справедливо z * ( f z) = 0. Следовательно, учитывая равенство X * = X ⁰ ® X ^s , для доказательства слабой непрерывности f в точке x достаточно для заданной неотрицательной последовательности z ⁰ = (z i , Z 2 ,...) G X ⁰ и числа e > 0 найти a(X, X * )-окрестность U точки x, для которой f (U) С O ( f x; z ⁰ , e). Рассмотрим последовательность y = (y i , y ₂ ,...) G X ⁰⁰ , определенную в ( * ). В силу сходимости ряда ^£i =₁ z i y i найдется N >  n g , для которого P i = N +1 z i y i <  4 . Положим M = max { P N =1 z i , 1 } . Существует 5 > 0 такое, что неравенства | x i — u | 6 5 влекут | f (i, x i ) — f (i,u) | 6 2 ^ для всех i = 1, N. Тогда для произвольного z G O (x; e i ,..., e N , 5) имеем | x i — z i | <5 для i = 1, N, откуда

^

| z ⁰ ( f x — f z) | =

X z i (f (i, x i ) — f (i,z i )) i =1

N                   ^          N

² ²

2 + 2 =

• ⁶ J2z i ^|f(i>x i ) ^{— f(i,z} i ^{)| +2} 52 z i y i < ₂M52z ' ⁺ 2

i =1                            i = N +1              i =1

Таким образом, f ( O (x; e ₁ ,..., e N , 5)) С O ( f x; z ⁰ , e), что и требовалось. B

Будем говорить, что оператор T , действующий в некотором банаховом пространстве Z , обладает конечномерной областью значений, если линейная оболочка множества R(T) = { Tz : z G Z } является конечномерным пространством. Пусть функция f : N х R ^ R определяет оператор суперпозиции f , действующий в пространстве последовательностей X. Если f (n, • ) = 0 при больших n, то, очевидно, f обладает конечномерной областью значений.

Следствие 10. Для любого бесконечномерного пространства последовательностей X существует, действующий в X , оператор суперпозиции f , являющийся слабо непрерывным и не представимый в виде суммы аффинного оператора и оператора, обладающего конечномерной областью значений.

C Существует последовательность x = (x 1 ,x 2 ,...) G X ° П X ⁰⁰ , причем x n > 0 при всех n. Действительно, если последовательности y и z — слабые единицы X ° и X ⁰⁰ , соответственно, то достаточно положить x n = min (y _n , z _n ). Для произвольного n G N найдем функцию f _n G C b (R) не являющуюся аффинной и такую, что k f _n k c _b ( R ) 6 x _n ; например, f _n (u) = x n sin u. Положим f (n, u) = f _n (u). В силу предыдущей теоремы, оператор суперпозиции f , определяемый f , является слабо непрерывным. Пусть g — аффинный оператор суперпозиции, действующий в X и определяемый функцией g . Тогда, как отмечалось выше, g(n, • ) аффинная для всех n, а значит функция h(n, u) = f (n, u) — g(n, u)

не является константой по u. Следовательно, существует последовательность u n , для которой h(n, u n ) = h(n, 0). Тогда h (u n e n ) — h 0 = (h(n, u n ) — h(n, 0))e n . Таким образом, оператор суперпозиции h = f — g не обладает конечномерной областью значений, как и требовалось. B

Следствие 11. Пусть функция f : R ^ R является ограниченной и непрерывной, f (0) = 0. Тогда оператор суперпозиции f , определяемый f и действующий в со, является слабо непрерывным.

C Требуемое утверждение сразу вытекает из теоремы 9, если заметить, что (с о ) ° = с о и (со)" = ' ^ . B

В силу следствия 7 предположение об ограниченности f существенно.

Неясно, справедливо ли утверждение обратное к теореме 9, т. е. вытекает ли из слабой непрерывности f его представление в виде f x = a + bx + f o x, где a = f 0, b — некоторая последовательность, а для оператора суперпозиции f 0 выполняются условия (a) , (b) и (c) теоремы 9. Для пространства ' ^ ответ частично был получен в [6]. В общем случае, положительный ответ на этот вопрос означал бы, что если f : R ^ R определяет в некотором пространстве последовательностей X слабо непрерывный оператор суперпозиции f , то f представима в виде f (u) = a + bu + g(u), где a,b E R, а g — ограниченная функция, g(0) = 0. Причем, в некоторых случаях, как, например, когда для любой x E X " выполняется liminf | x i | = 0 (см. следствие 2) или когда последова- i ^^

тельность (1,1,...) E X \ X ° , было бы g = 0. В частности, следствие 11 давало бы не только достаточное, но и «по сути» необходимое условие слабой непрерывности оператора суперпозиции f в с о . Тем не менее, вопрос остается открытым даже для случая пространства с о и функции f : R ^ R.

Частичное подтверждение справедливости отмеченной гипотезы дает теорема 8. В самом деле, если двойственное к пространству последовательностей X пространство X' является инвариантным относительно растяжения, то, очевидно, X " С ' ^ . Кроме того, как следует из теоремы 9, теорема 8 не остается справедливой для произвольного X. Достаточно заметить существование пространства последовательностей X , для которого X = X ° и X " * ' ^ . Например, пространство с о с весом,

X = <  x = (x 1 , x ₂ ,...) : lim n 1x _n = 0 и ||x|| = sup | n 1 x _n | <  ro >  . n ^^                  n

Как легко видеть, последовательность (1, 2, 3,...) E X". Таким образом, равенство ( * ) в теореме 8 может иметь место для слабо непрерывного оператора суперпозиции f , определяемого функцией f >  0.

То обстоятельство, что для пространства ' ^ и функции f : R ^ R ответ получен, а для с о еще нет, может быть объяснено более большим сопряженным к пространству ' ^ . Действительно, с о = ' 1 С ' ^ Пространство ' ^ , конечно, более сложное, чем ' 1 , но оно содержит и более специальные функционалы за счет свойств которых можно получить более глубокие результаты о слабой непрерывности оператора суперпозиции f . Так, в [6] при установлении аффинности функции f : R ^ R, порождающей слабо непрерывный оператор суперпозиции f , действующий в ' ^ , решающую роль играло существование на ' ^ обобщенных пределов, являющихся антинормальными функционалами. Функционалов «такого вида» не существует на с о .

Следующая теорема дает условия, при которых функция f удовлетворяет предположению (c) из теоремы 9. Через s будем обозначать пространство всех последовательностей, а через Г линейную оболочку множества {en}n=1 в s. Если X — некоторое про- странство последовательностей, то, очевидно, Г С X0, а значит пара (X, ri образует дуальную пару.

Теорема 12. Пусть функция f : N х R ^ R определяет оператор суперпозиции f , действующий в пространстве последовательностей X, причем f 0 = 0. Рассмотрим следующие утверждения :

• (a)    Оператор f является непрерывным, как отображение топологического пространства (X, a(X, Г)) в топологическое пространство (X, a(X, X 0 ));

• (b)    Оператор f является непрерывным в нуле, как отображение топологического пространства (X, a(X, Г)) в топологическое пространство (X, a(X, X ⁰ ));

• (c)    Имеет место включение f (s) С X ⁰⁰ ;

• (d)    Для функции f выполнено условие (c) теоремы 9.

Тогда (a) ^ (b) ^ (c) ^ (d) .

Если, к тому же, f удовлетворяет условию Каратеодори, то (d) = ^ (a) .

• <1 (a) ^ (b) Очевидно.

• (b)    ^ (c) Всякая последовательность x из пространства Рисса s может быть представлена в виде x = y + z, y ± z, причем f у >  0 и f z 6 0. Следовательно, включение f x G s достаточно показать в предположении f x >  0. Определим последовательности Z n = (x i ,..., x n 0, 0,...) G X и Z k,m = Z k — Z m . Очевидно, z km ^ ( -H ) 0 при k,m ^ ro , а значит f Z k,_m -- X ) 0. При этом для k >  m имеем f Z k,_m = f z k — f z m . Следовательно, f z k является слабой последовательностью Коши, в частности, последовательность x ⁰ f z k ограничена для произвольного функционала x ⁰ = (x 1 ,x⁰ ₂ ,...) G X 0 . Для x ⁰ имеет место интегральное представление xy = Hx i xy i = / x ⁰ у d^ для всех у G X, где ц — «счи-

• N

тающая» мера на N. Используя теорему Фату [3, с. 169] и соотношения 0 6 f z k f f x получаем ^21 =₁ x i ( f x) i = /x ⁰ f xd^ <  ro , откуда f x G X ⁰⁰ .

N

• (c)    ^ (d) Прежде всего покажем, что начиная с некоторого номера функции f (n, • ) ограничены. В предположении противного найдем подпоследовательность n k натуральных чисел, для которой функции f (n k , • ) неограниченные при всех к. Существует неотрицательная последовательность x = (x i ,x 2 ,...) / X ⁰⁰ такая, что x i > 0 в том и только том случае, когда i = n k при некотором к. Действительно, взяв произвольный элемент z = (z 1 , z 2 , . . .), являющийся слабой единицей в X ⁰ , достаточно положить x n k = z^ и x i = 0 при i / { n 1 ,n 2 ,... } . Существует последовательность u n , для которой z _nk

| f (n k ,u n k ) | >  x n k при всех к. Имеем 0 6 x 6 | f u | G X ⁰⁰ , где u = (u i ,u 2 ,...) G s. Поскольку X ⁰⁰ — идеал в s, получаем x ∈ X ⁰⁰ . Мы пришли к противоречию. Таким образом, существует n g такое, что для всех n > no функции f (n, • ) ограничены.

Положим b n = ||f (n, • ) k c _b ( R ) при n > ng и b n = 0 для остальных n G N. Найдем последовательность e = (E 1 ,E 2 ,---) G c g П X ⁰⁰ такую, что b n > e n > 0, если b n > 0, и e n = 0, если b n = 0. Для некоторой последовательности u n будет | f(n, u _n ) | >  b n — e n при всех n. Тогда 0 6 b — e 6 | f u | G X ⁰⁰ , где b = (b ₁ , b ₂ ,...), u = (u ₁ , u ₂ ,...). Значит b — e G X ⁰⁰ , откуда b ∈ X ⁰⁰ .

• (d)    ^ (a) Доказательство аналогично доказательству теоремы 9. B

Предыдущая теорема не противоречит результатам полученным ранее и говорящим, что в некоторых случаях слабая непрерывность равносильна аффинности (например, теорема 1 и следствие 2). На самом деле, аффинное отображение Tx = a + bx будет непрерывным, как отображение (X, a(X, Г)) в (X, a(X, X ⁰ )) в том и только том случае, когда b G Г, т. е. b n = 0 при больших n. В пояснении нуждается лишь необходимость.

В предположении противного положим z n = b n , если b n = 0, и z n = 1, если b n = 0. Тогда ^ ( Х, Г)

последовательность x n = z ц_е ц e n —» 0, но неограниченная последовательность T x n не может сходится к элементу а в a(X, X ⁰ )-топологии. Для этого достаточно заметить, что иначе мы получили бы и слабую сходимость Tx _n к a, а значит ее ограниченность. В частности, тождественный оператор I не является непрерывным, как отображение (X,a(X, Г)) в (X,a(X,X 0 )).

Имеет место также следующее утверждение, доказательство которого аналогично доказательству импликации (b) = ^ (c) теоремы 12: Если оператор суперпозиции f , действующий в пространстве последовательностей X , является слабо непрерывным, то f (X 00 ) С X ⁰⁰ . На самом деле, справедлив следующий более общий факт: Если Y — идеал в пространстве Рисса s, Г С Y, оператор суперпозиции f непрерывен, как отображение (X, a(X, Y)) в (X, a(X, X 0 )), то f (Y 0 ) С X ⁰⁰ . Здесь, по аналогии со случаем пространства последовательностей, Y ⁰ = { z Е s : 52^ =1 Z i y i <  го , y Е Y } .

Отметим, что некоторые результаты статьи без труда могут быть перенесены на случай, когда оператор суперпозиции f действует из одного пространства последовательностей X в некоторое другое пространство последовательностей Y .

Итак, хотя для случая непрерывной меры ответ полностью получен, в случае дискретной меры при исследовании слабой непрерывности оператора суперпозиции возникают определенные трудности. Данный факт является еще одним подтверждением в пользу точки зрения о том, что дискретное сложнее, чем непрерывное.