Clustering matrix sequences based on the iterative dynamic time deformation procedure

Published Online July 2018 in MECS

The development of information technology has led to a rapid growth in volumes of data processed. There is a sufficient amount of approaches for text data, but the multimedia analysis, and especially a technique used for a case when it is necessary to take into account the data content (content-based approaches) has not been widely developed yet. This problem is especially typical for video data processing due to the maximum hardness of the analysis process in a time-limited environment [1-4].

Moreover, the complexity is rather high not only due to big data volumes, but also due to their insufficient structuredness, and therefore there are whole sets of scenes (shots) within a single video sequence that are weakly correlated or not correlated at all with each other. At the same time, the correlation within the same shot remains rather strong [5]. So if you need to solve some problems, for example, to search for a content in video data, there are serious time limits. To accelerate the analysis in the domain of video sets, some preliminary processing is required which allows speeding up the process considerably. Since it can be an offline video clustering/segmentation procedure to represent a video as a set of content-homogeneous segments [6-18]. Given the fact that any video sequence can be represented in the form of a sequence of frames, it is advisable to use the multidimensional (matrix) time series analysis [19, 20].

The aim of clustering time series holds a specific place in the whole domain of Data Mining [21-23]. For the purposes of time series clustering, there are multiple methods to have been proposed and examined which are distinct from each other by the initial assumptions, by the mathematical apparatus applied, and by the computational complexity of their actualization [8-11]. In particular, this problem takes a peculiar place in the analysis of video sequences where most of the known techniques lose their efficiency. It can be justified in the first instance by the fact that high demands on performance step forward in the context of large volumes of processed data, and actual clustering objects are matrix time series X ₁ , ,X_q ,X_r , ,X_Q , and each one contains N ₁ , ,N_q ,N_r , ,N_Q observations in such a way that X r = { x r (1) ,x r (2)..., x r ( k ) ,...,x r ( N r ) } , and every individual observation is revealed as a ( n x m ) - matrix X r ( k ) = { 4 ( k ) } i 1 = 1 , 2 ,...,n, i 2 = 1 , 2 ,-.-,m .

At the same time, the major challenges to appear while clustering time series are determined by the fact that these series are distinguished by different lengths and mainly not so much by the high dimensionality of the data being processed. For instance, if a series X stores N

(n x m) -matrices of video snapshots, then a series Xr contains  Nr  matrices of the same dimensionality subsequently that doesn’t make it possible to use a residual quantity A = Xq - Xr to determine similarity between them as well as to take an advantage of the known norms of this residual accordingly. As an alternative way to traditional norms, it can be some certain proximity rate [11, 24-27]. A method of the Dynamic Time Warping (DTW [28-36]) may be one of the aforesaid proximity measures. This technique is chiefly grounded on the Euclidean norm to be calculated between two vectors of observations. It is conceivable that a spherical norm (which is an extension of the Euclidean one) may be used in the event of matrix observations.

In such a way, if two sequences X_q and X are given with            the            property            that

X q = { X q (1) ,X q t ² )-, X q ⁽ k ) ^,..^.,X q ⁽ N q ) }                  and

Xr ={xr(1),Xr (2)...,Xr(1),...,Xr (Nr)} , Nq * Nr , it is possible to employ the DTW method for estimation of their similarity or dissimilarity. For that to happen, let’s force into application a (Nq x Nr) -matrix of distances with                                         elements d (Xq (k) ,Xr (l ))= ( SP (Xq (k) — Xr (1))(Xq (k) - Xr (1)) T )12 .     A

«warping path» is defined by this matrix to be determined by a sequence of elements

W = { W 1 ,W 2 ,..,W l } ,W t = d ( X q ( k ) , X r (l )) t , maX ( N_a,N, .) <  L <  N + N + 1 ,t = 1 , 2 ,...,L. qr      q  r

This being said, the smaller it is, the closer (similar) X_q and X_r are to each other. This path is governed by minimization of a criterion

DTW ( X q ,X r ) = min ^ qr  _W

L ^ d (Xq (к ),Xr (1)) t - to be implemented through a recurrent procedure of the dynamic programming

D ( k,l )= d ( x q ( k ) ,x r ( l ))+

+ min {D (k, 1 -1), D (k -1, 1), D (k -1,1 -1)} where D(k,l) denotes cumulative distances between elements of the sequences and xq(k),xr(l) .

Apparently,

DTW ( X q ,X r )= D ( N q ,N r ) .          (1)

The approach to clustering time series in terms of DTW affirmed it to be effective for solving a set of classical problems [11] (for both a one-dimensional case and a vector one). Although it’s fairly obvious that it loses its effectuality in the event of sufficiently long matrix sequences, since it may require high computational efforts.

The remainder of this paper is organized as follows. Section 2 describes a modified iterative dynamic time warping method. Section 3 is devoted to clustering reduced matrix time series. Section 4 presents an experimental research of the work. Conclusions and future work are given in the final section.

• II.    A Modified Iterative Dynamic Time Warping Method

An idea of the Iterative Dynamic Time Warping method consists in reduction of initial time series [37]. For this purpose, the time series analyzed are primarily divided into four sections, and the time series is replaced by its average values in each section. Thus, the time series X_q and X_r are replaced by the sequences X_q and X_r where each one embodies four segments x _q (1), x _q (2), x _q (3), x _q (4) and x _r (1), x _r (2), x _r (3), x _r (4) correspondingly. Closeness between two series X_q and X_r is further estimated according to a ( 4 x 4 ) - matrix of distances, with that

DTW ( X _q ,X _r ) = DTW (4,4).

If the results obtained don’t meet the requirements, every segment x _q ( k ) , x _r ( k ) is halved, and the distance is estimated again

DTW ( X _q ,X _r ) = DTW (8,8) .

The process of halving segments goes underway until the required accuracy of the result is obtained. That said, an amount of analyzed segments grows at an exponential rate.

From the computational point of view, it is much easier to split the original series in such a way that a number of sections grows in an arithmetic progression [2, 38, 39]. Thereby , ther e are sequences obtained X ₁ , ,X_q ,X_r , ,X_Q as a result of the reduction procedure, where each one embodies S regions X q = { X q (1) ,X q (2)...,X q (S) } , X r = { x r (1) ,^ r (2)..., X r (S) } . Although the series X_q and X_r encapsulate an equal number of regions, it is unacceptable to apply the spherical norm D ( X_q,X_r )= ( Sp ( X q - X,. )( X q - X r ) ^T ) ¹ to estimate a distance between them, since regions of both series are characterized by different lengths.

In a related move, a modification of the assessment (1) can be utilized in the view of

DTW ( X q ,X r )= D (S ,S ^ = D ( X _q ,X _r ).      (2)

Understandably, any other esteem (traditionally exploited for analysis of time sequences [2]) can be involved instead of the traditional arithmetic mean for each segment of the time series.

• III.    Clustering Reduced Matrix Time Series

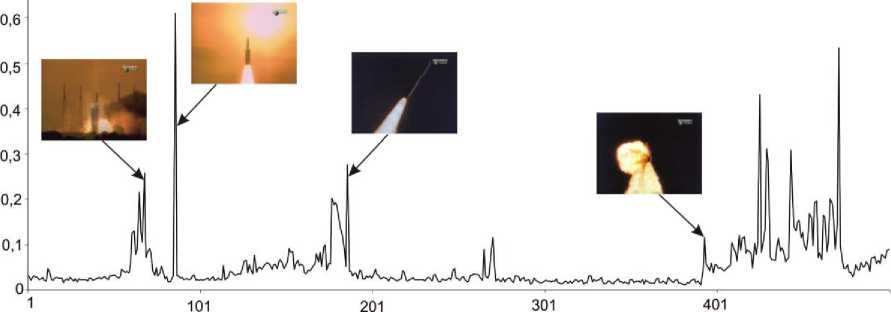
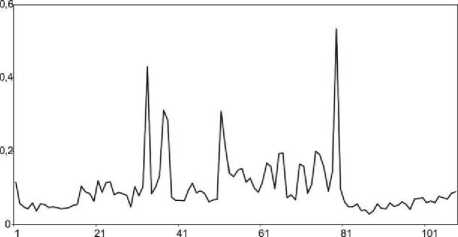
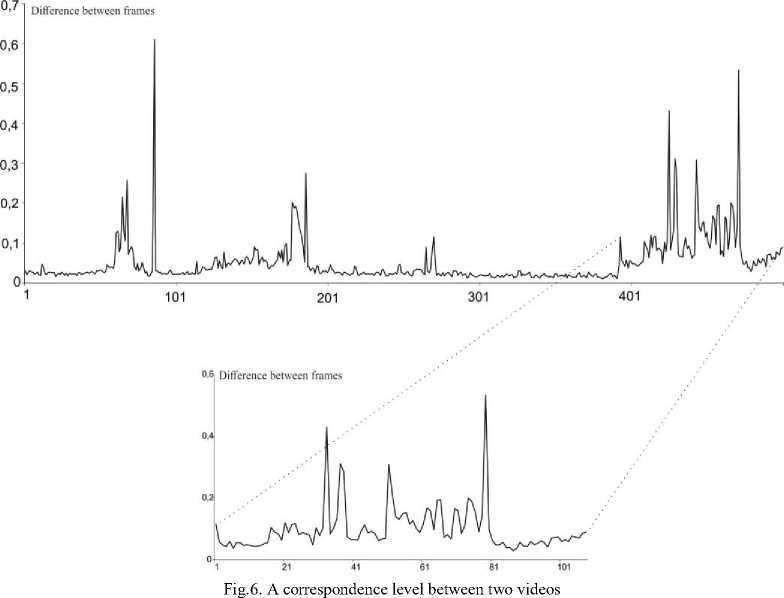
Xq e Clj    if    D(Xq,cj)

Initial centroids c ,c are chosen in a quite arbitrarily way. The clustering process is particularly a sequence of iterations, where centroids’ coordinates are being recounted.

For instance, the objective function

Qm

E(Xq,Cj )= EE Uj (q)D²(Xq,Cj)           (3)

q=1 j=1

is minimized in the process of adjusting centroids in the case of the k -means clustering.

And centroids based on mean values are recalculated at every iteration of the procedure according to a relation

E X =

Nj X_q eClj

Q

E uj( q )Xq q=1______________

Q

E uj⁽q)

q=1

where uj (q) marks a crisp membership function for the time series to the j -th cluster. In this case, uj(q)=

1 if X_q e Clj

0 otherwise.

Along with that, it is mentioned in [8-11] that the methods grounded on average medians are extremely sensitive to an ineffectual choice of initial centroids in such a way that the clustering process may require a larger number of iterations which is completely unacceptable when it comes to processing large arrays of video information.

Another possible choice is the clustering procedure [41, 42] based on application of harmonic means, in which case a harmonic mean may be presented as x =

E x^-1(q)

q=1

for a sequence of scalar observations x₁,  ,x_Q.

The algorithm offered by B. Zhang and co-authors [40, 41] for an array of vector observations can be updated for clustering matrix objects X₁, ,X_q,X_r, ,X_Q , where each X_q has a dimensionality of (n x ms), and a distance between X_q and a centroid c_j is estimated with the help of D(X ,c ) according to the expression (2). Upon that, an objective function

Q

^E(X-O ^Z  ----j---         (5)

q=1 у_____1_____ jУ D2(Xq,Cj)

is minimized during data processing. The mentioned objective function is based on the distance D²(X_q,c_j) just like the function (3).

Minimizing the function (5) by the matrix c , it leads to the estimate

ED-4(Xq,Cj)( ZtD "²(Xq,Cj))-²Xq

P = q=1_________________j=1________________________ cj     Q -   -      m -   -          ,

E D-4(Xq,Cj)(E D"²(Xq,Cj))^-2

q=1                     j=1

which is also figured out as a result of a set of iterations (similarly to the expression (4)), although their quantity does not largely depend on initial conditions [10, 11]. The authors are introducing the modification (6) in the view of

^Ld "“ (Xq,Cj)( ETD -2(Xq,Cj)) -2 Xq p = q=1__________________j=1________________________ сj    Q _   _      m _   _

E D - (Xq,Cj )( E D "²(Xq,Cj ))^-2

q=1                     j=1

where an argument a has a point close to a fuzzifier value that is traditionally utilized in fuzzy clustering procedures.

It does not look difficult to examine fuzzy updates of the procedures (6) and (7) in terms of the approach covered in [8]. At this point, a fuzzy membership level of the q -th time series to the j -th cluster can be computed in obedience to uj(q)=

D "4Xq,Cj)

m

ZD-2(Xq,Cj)

j=1

for the centroids (6) and uj(q)=

(D 2(Xq,Cj))1^-e m¹ Z (D4Xq,Cj))^-^ j=1

for the expression (7). In this case, в > 0 stands for a fuzzifier magnitude (a fuzzification parameter) to specify borders’ smearing between the formed clusters.

It should be noted that obtaining the esteems (6) and (7) is not more complicated than evaluation of the centroids in the k -means algorithm from a computational standpoint, but it requires fewer iterations.

• IV.    Experiments

To conduct an experiment for testing the proposed approach, a video clip database was created on the grounds of the series “Destroyed in Seconds” by the Discovery Chanel. A choice of such a movie clip was specified by a fast-changing video and the presence of some scenes with similar characteristics within a single video sequence. Fig.1 shows several video sequences from the database. In this case, as an example, several frames with similar characteristics are shown for some segments of each video sequence that display the processes occurring in the video from the usual shooting of the event to the disaster.

Fig.1. Examples of video sequences presented by a set of frames from the database

Further, for all sequences from the database in an offline mode, the spatio-temporal segmentation of video sequences is implemented. These preliminary calculations are necessary for the early detection of properties’ changes in the source data for information retrieval. An example of the spatial segmentation for an initial video sequence is demonstrated in Fig.2. And Fig.3 presents the results of the temporal segmentation. As one can see, peaks (in Fig.3) make it possible to determine changes (it can be seen from the provided video frames) in a homogeneous shot by a content of the sequences. It should be noted that either if changes occur smoothly in the original video data, or if data are noisy, the procedures of the spatio-temporal segmentation do not always provide adequate results.

Fig.2. Examples of video sequences and the spatial segmentation of video frames

0,7

Difference between frames

Fig.3. Differences between frames of a video sequence as result of the temporal segmentation

Further, to check the proposed method, a reduced video sequence was taken, for example, a moment of a catastrophe shot from several angles. An example of such a video sequence is shown in Fig.4. The IDTW method makes it possible to compare this video sequence of a different length with a set of video sequences from the database and to find the most relevant results after the clustering procedure has been applied. The results of the clustering/segmentation presented in Fig.5 demonstrate a correspondence level between this video and the one in Fig.3 (Fig.6). To be mentioned, the required result was obtained as a result of comparison of the video sets using the proposed modified IDTW procedure.

Since the comparison result cannot be a single video from the database, because it contains various videos of similar disasters, the next step was to test a number of video fragments with the video database using the developed IDTW clustering method. To evaluate the results obtained, a standard approach was used (also known as “Precision and recall”). This approach evaluates the correctness of the comparison results by finding a difference between relevant and irrelevant query results. Accordingly, these values are defined as

P = -IP-, R = -1P-tp+fp tp + fn where tp is a true positive result, fp denotes a false positive result, and fn stands for a false negative result. In this case, these values are not used in practical tasks and some measures created on their basis are used for evaluation of the final result. For example, the F-measure [43] (also called the harmonic mean) is calculated as

This measure is approximately an average value of the precision and the recall when they are close enough.

Fig.4. An example of a reduced video sequence

The results of the experiment for clustering 10 video fragments of different lengths and comparing them with the video base with further calculation of the described F-metric are presented in Table 1. If the arithmetic average of the obtained results is then chosen, a value of the F-measure equals to 0.8707. From the point of view of the information content, this result is quite satisfying for the clustering video sequences.

Table 1. Results of clustering

A video’s number	F-measure
1	0.876
2	0.922
3	0.831
4	0.915
5	0.807
6	0.862
7	0.838
8	0.946
9	0.847
10	0.863

At the same time, a rather vast range of values can be explained by several reasons. First of all, an amount of objects in the video database may not be sufficient that leads to roughened results in the precision and the recall. This fact is reflected by a distribution of the F-measure values. Secondly, the heterogeneity and ambiguity of videos while clustering data by the content adds some additional difficulties when it comes to searching of the similar data in terms of their characteristics. Thus, taking into account the indicated complexity, the results obtained are quite sufficient for being further applied as well as the given simplicity for implementation of the proposed modified iterative dynamic time warping approach for clustering matrix sequences.

Fig.5. An example of clustering the reduced video sequence

V. Conclusion

Acknowledgment

The clustering method for the video sequences adapted from the modified Iterative Dynamic Time Warping technique and the succeeding clustering of reduced time series driven by the matrix fuzzy clustering method of the harmonic k -means is presented. A key feature of the developed approach is its plainness of numerical realization (compared to the prototype-based method), which is extremely important for processing video sequences.

This scientific work was financially supported by selfdetermined research funds of CCNU from the colleges’ basic research and operation of MOE (CCNU16A02015). The third author also acknowledges the support of the Visegrad Scholarship Program—EaP #51700967 funded by the International Visegrad Fund (IVF).