Cogging Torque Reduction in Surface Permanent Magnet Motors Using Taguchi Experiment Design and Finite Element Method

Published Online October 2012 in MECS

Today, surface permanent magnet motors because of the torque to weight ratio and high reliability and high efficiency, which are widely used in industrial applications [1]-[4]. However, in this type of motors the cogging torque is one of the main obstacles in usage development. The cogging torque arises from the interaction of the stator teeth with magnets that causes the increasing the torque ripple, noise, vibration and ultimately reduce motor efficiency.

For SPM motors, the reduction of cogging torque is a critical theme for study. The cogging torque is greatly affected by the shape of the magnets. The permanent magnet poles and stator slots shape in this motors is the main cause of cogging torque production. A lot of techniques have been proposed to reduce the cogging torque in surface permanent magnet motors. Some of these techniques [8]-[11] are to modify the rotor and permanent magnet poles shape and some of other techniques [12], [13] are to modify the stator shape.

In this paper, by using the Taguchi experiment design method, optimization simultaneously on the permanent magnet poles and stator grooves of a surface permanent magnet motor with four poles and six slots is done. This type of surface permanent magnet motor now widely is used in air conditioning compressors [5]. Compared to

SPM Motor and Taguchi method

SPM Motor

The application of surface permanent magnet motors is expanding. They are used in some electric cards and electric power steering and also in a variety of industrial motors. The schematic diagram of SPM motor under study shown in Figure1 and the main parameters are shown in Table 1. Different from conventional windings, this kind of stator winding cannot produce symmetrical magnetomotive force (MMF) under the four poles, and more harmonics exist in the air gap, which will increase the torque ripple and noise.

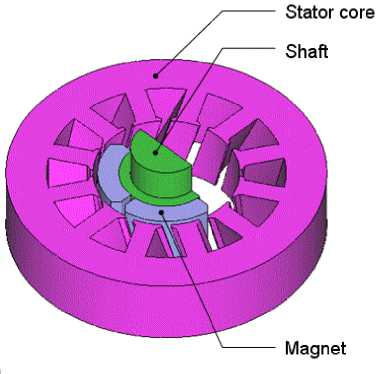
Fig. 1: The SPM motor with four-pole and six-slot

The torque and cogging torque waveform with variations in stator and magnet shapes have been computed using 2-D finite element analysis (FEA). The Taguchi method and simulations by using the finite element method has been done in this paper.

Taguchi method

Taguchi methods are statistical methods developed by Genichi Taguchi to improve the quality of manufactured goods and, more recently, to biotechnology, marketing and advertising. Taguchi methods are considered controversial among some traditional Western statisticians but others accept many of his concepts as being useful additions to the body of knowledge.

Taguchi' s principal contributions to statistics are:

• •     Taguchi loss-function;

• •    The philosophy of off-line quality control ;

• •     Innovations in the design of experiments.

Loss functions

Taguchi' s reaction to the classical design of experiments methodology of R. A. Fisher was that it was perfectly adapted in seeking to improve the mean outcome of a process. As Fisher' s work had been largely motivated by programs to increase agricultural production, this was hardly surprising. However, Taguchi realized that in much industrial production, there is a need to produce an outcome on target , for example, to machine a hole to a specified diameter or to manufacture a cell to produce a given voltage. He also realized, as had Walter A. Shewhart and others before him, that excessive variation laid at the root of poor manufactured quality and that reacting to individual items inside and outside specification was counterproductive.

He therefore, argued that quality engineering should start with an understanding of the cost of poor quality in various situations. In much conventional industrial engineering  the  cost  of poor  quality is  simply represented  by  the  number  of items  outside specification multiplied by the cost of rework or scrap. However, Taguchi insisted that manufacturers broaden their horizons to consider cost to society. Though the short-term costs may simply be those of nonconformance, any item manufactured away from nominal would result in some loss to the customer or the wider community through early wear-out; difficulties in interfacing with other parts, themselves probably wide of nominal; or the need to build-in safety margins. These losses are externalities and are usually ignored by manufacturers. In the wider economy the Coase Theorem predicts that they prevent markets from operating efficiently. Taguchi argued that such losses would inevitably find their way back to the originating corporation (in an effect similar to the tragedy of the commons) and that by working to minimize those, manufacturers would enhance brand reputation, win markets and generate profits.

Such losses are, of course, very small when an item is near to nominal. Donald J. Wheeler characterized the region within specification limits as where we deny that losses exist . As we diverge from nominal, losses grow until the point where losses are too great to deny and the specification limit is drawn. All these losses are, as W. Edwards Deming would describe them, unknown and unknowable but Taguchi wanted to find a useful way of representing them within statistics. Taguchi specified three situations:

• 1.    Larger the better (for example, agricultural yield);

• 2.    Smaller the better (for example, carbon dioxide emissions); and

• 3.   On-target, minimum-variation (for example, a

mating part in an assembly).

The first two cases are represented by simple monotonicloss functions. In the third case, Taguchi adopted a squared-error

Off-line quality control

Taguchi realized that the best opportunity to eliminate variation is during design of a product and its manufacturing process (Taguchi's rule for manufacturing) . Consequently, he developed a strategy for quality engineering that can be used in both contexts. The process has three stages:

• 1.    System design;

• 2.  Parameter design; and

• 3.  Tolerance design.

System design

This is design at the conceptual level involving creativity and innovation.

Once the concept is established, the nominal values of the various dimensions and design parameters need to be set, the detailed design phase of conventional engineering. William Sealey Gosset in his work at the Guinness brewery suggested as early as the beginning of the 20th century that the company might breed strains of barley that not only yielded and malted well but whose characteristics were robust against variation in the different soils and climates in which they were grown. Taguchi's radical insight was that the exact choice of values required is under-specified by the performance requirements of the system. In many circumstances, this allows the parameters to be chosen so as to minimize the effects on performance arising from variation in manufacture, environment and cumulative damage.

Design of experiments

Taguchi developed much of his thinking in isolation from the school of R. A. Fisher, only coming into direct contact in 1954. His framework for design of experiments is idiosyncratic and often flawed but contains much that is of enormous value. He made a number of innovations.

In his later work, R. A. Fisher started to consider the prospect of using design of experiments to understand variation in a wider inductive basis . Taguchi sought to understand the influence that parameters had on variation, not just on the mean. He contended, as had W. Edwards Deming in his discussion of analytic studies, that conventional sampling is inadequate here as there is no way of obtaining a random sample of future conditions. In conventional design of experiments, variation between experimental replications is a nuisance that the experimenter would like to eliminate whereas, in Taguchi' s thinking, it is a central object of investigation.

The Taguchi method by using orthogonal array tables extremely reduced the number of experiments.This array of special features among the total number of experiments is selected. It is noteworthy that the answer does not necessarily optimal in there and selected experiments using the Taguchi method of calculation of the array experiments can be answered in optimal conditions and to determine the optimal conditions and at the end by Confirming test, confirming its accuracy can be obtained comes [6],[7].

Table 1: Parameters of the SPM motor

Rated power	20 KW
Stator outer diameter	110 mm
Stator inner diameter	60 mm
Lamination length	68 mm
PM thickness	1.65 mm
Air gap length	0.5 mm

• II.    Design Factors

The design factors and their respective levels are given in Table2.

• A.    is the ratio of magnet pole arc to pole pitch

• B.    is the distance from motor center used as the center of circle for magnet in millimeters

• C.    is the slot opening height in millimeters

• D.    is the slot opening width in millimeters

• E.    is the air gap length in millimeters

  There are 16 experiments (A standard Taguchi ʼ orthogonal array L-16) required to determine the optimum combination of the levels of these factors as shown in Table 3 and to know the contribution of each to produce the values of average torque and cogging torque. However in comparing with experimental frequency of optimization methods, if there are five variables each at four levels, full factorial approach needs 1024 experiments. On the other hand, the Taguchi method can obtain satisfactory results by only sixteen times that saves considerable time of simulation to reach the optimal point.

Table 2: Design Factors

Factors	Level 1	Level 2	Level 3	Level 4
A	0.75	0.8	0.86	0.92
B [mm]	0	0.16	0.32	0.47
C [mm]	0.8	0.88	1.05	1.1
D [mm]	1.7	1.85	1.9	2
E [mm]	0.3	0.38	0.52	0.63

Table 3: 16 experiments Array

Experiment	A	B	C	D	E
1	1	1	1	1	1
2	1	2	2	2	2
3	1	3	3	3	3
4	1	4	4	4	4
5	2	1	2	3	4
6	2	2	1	4	3
7	2	3	4	1	2
8	2	4	3	2	1
9	3	1	3	4	2
10	3	2	4	3	1
11	3	3	1	2	4
12	3	4	2	1	3
13	4	1	4	2	3
14	4	2	3	1	4
15	4	3	2	4	1
16	4	4	1	3	2

• III.    Analysis of Simulation Results

After conducting the matrix experiment and obtaining all the simulation results, analysis of means (ANOM) and analysis of variance (ANOVA) are carried out to estimate the effects of the four design parameters and determine the relative importance of each design variable, respectively.

The means of all simulation results can be calculated as:

m

= —  T

16 ^^

Table4 tabulates the results. The value of average torque of setting variable A at level 3 is calculated by (2).

Where, the factor A is set to level 3 only in experiments 9, 10, 11, 12. Average torque of all variables can be obtained by a similar way. Table5 shows the results. A plot of main factors effects is illustrated in Figure 2. It is seen that the factor-level combination (A4, B1, C4, D2, and E1) contributes to maximization of average torque.

Table 4: Analysis of Means

Tc (N.m) Tavg (N.m) m 0.69 3.92 тАз( Tavg ) = 1( Tavg (9) + Tavg (10) + Tavg (11) + Tavg (12))

Table 5: Average torque

	Ai	Bi	Ci	Di	Ei
i=1	3.92	3.94	3.91	3.92	4.1
i=2	3.83	3.93	3.90	3.92	3.96
i=3	3.8753	3.91	3.93	3.92	3.87
i=4	4.0276	3.89	3.92	3.92	3.79

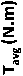
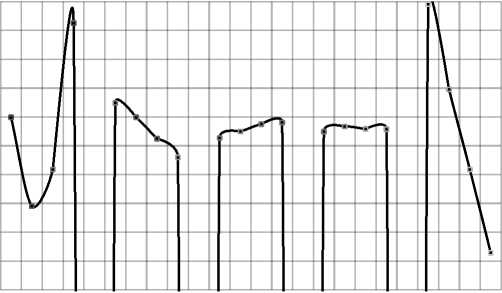
setting of factors

Fig. 2: Main factor effects on average torque

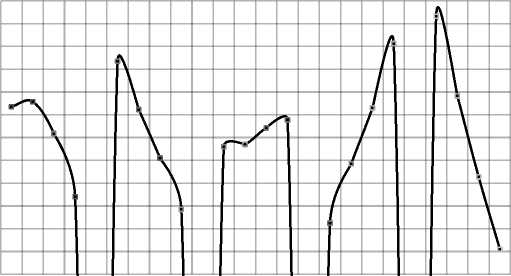
setting of factors

Fig. 3: Main factor effects on peak to peak value of cogging torque

The peak to peak value of cogging torque can be obtained for all levels of factors. Figure 3 illustrates the main factor effect on the peak to peak value of cogging torque.

An important purpose of ANOVA is to determine the relative importance of the various design variables. To conduct ANOVA, the sum of squares (SS) is calculated first. It is measure of the deviation of simulation data from the mean value of the data. The sum of squares (SSF A ) due to various factors can be calculated as:

SSFA = 4 ^ ( m^ - m )²

SSF B , SSF C , SSF D and SSF E can be obtained in the same way. These results show in Table7.

Table 7: Effects of all factors

	Tavg (N.m)		Tc (N.m)
	SSF	Factor effect (%)	SSF	Factor effect (%)
A	0.0820	34	0.00443	2.8
B	0.0074	3	0.02700	17
C	0.00065	0.3	0.00108	0.67
D	0.00005	0.02	0.03300	20.5
E	0.15	62	0.09500	59
Total	0.2401	100	0.16051	100

• IV.    Magnetic Field Analysis and Optimization

After the motor has been properly modeled, a 2D FEM magnetic field calculation is performed. The distribution of the magnetic field is presented in Figure. 4.

The performance of the optimized machine was obtained using FEM analysis again and compared with the initial one. Table8 compares the data of the machine between the initial, Taguchi parameter designs and simulation results.

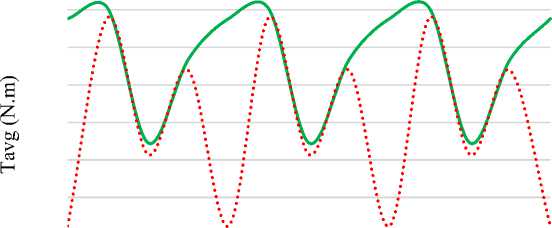
It can be seen that average torque increases from the initial design of 3.8276 Nm to Taguchi parameter design of 4.1118 Nm, and to simulation result of 4.1460 Nm. The peak to peak value of cogging torque decreases from the initial design of 0.7311 Nm to Taguchi parameter design of 0.6391 Nm, and to simulation result of 0.6349 Nm.

Table 8: Comparison Results

	Tavg (N.m)	Tc (N.m)
Initial	3.83	0.7
Taguchi results	4.10	0.64
Simulation results	4.15	0.60

For better comparison result, output torque ripple has been calculated before and after optimization. Output torque ripple calculated from division of the rms value to average output torque.

Value of output torque ripple has been compared in table9. The output torque ripple after optimization has 38.68% considerable decrease. Graphic performance comparison the average torque between initial and optimized design is given in Figure 5.

Figure6 Compares the cogging torque between initial and optimized design.

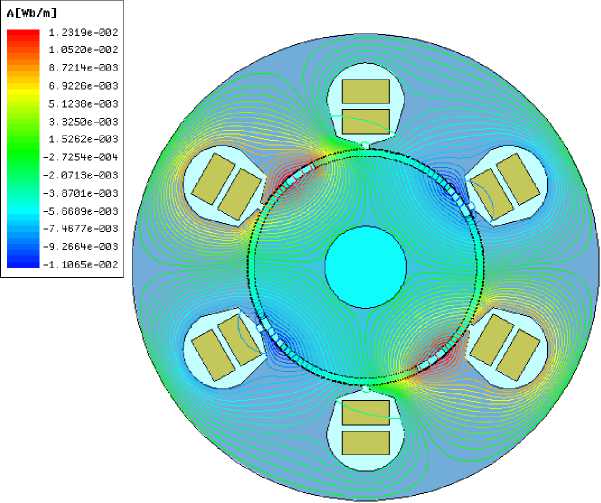
Fig. 4: Magnetic field distribution for SPM motor

Table 9: The Comparison of Output Torque Ripple before and After Optimization

	AC rms value (N.m)	Output ripple torque (%)
Initial	0.424	11.093
Result after optimization	0.282	6.802

Time(ms )

Fig. 5: Output torque of initial design (red line) and optimized design (green line)

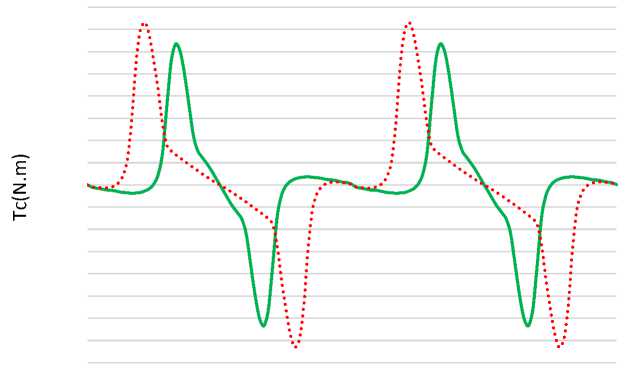
Fig. 6: Cogging torque of initial design (red line) and optimized design (green line)

V. Conclusion The reduction of cogging torque is a critical theme for SPM motors study. The cogging torque is greatly affected by the shape of the magnets. This paper applied the Taguchi methods to design optimization of SPM motor for the minimization the cogging torque. For better comparison result, output torque ripple has been calculated before and after optimization. Output torque ripple calculated from division of the rms value to average output torque.

Because of using Taguchi method, we have least of simulations for optimal design. Comparison of result before and after optimization shows, decrease of peak to peak value of cogging torque, increase average output torque. The output torque ripple after optimization has 38.68% considerable decrease. References [1] K. Ogasawara, T. Murata, J. Tamura, and T. Tsuchiya, “High performance control of permanent

magnet synchronous motor based on magnetic energy model by sliding mode control,” in 2005 Eur. Conf. Power Electronics and Applications, Sept. 2005, p. 10.

• [2]    B. Stumberger, G. Stumberger,M. Jesenik, V. Gorican, A. Hamler, and M. Trleps, “Power capability and flux-weakening performance of interior permanent magnet synchronous motor with multiple flux barriers,” in Proc. 12th Biennial IEEE Conf. Electromagnetic Field Computation, 2006, p. 419.

• [3]    Y. K. Chin and J. Soulard, “A permanent magnet synchronous motor for traction applications of electric vehicles,” in IEEE Int. Conf. Electric Machines and Drives, June 2003, vol. 2, pp. 103.

• [4]    B. N.  Chaudhari and B. G. Fernandes,

  “Performance of line start permanent magnetsynchronous motor with single-phase supply system,” Proc. Inst. Electr. Eng., Electr. Power Appl., vol. 151, no. 1, pp. 83–90, Jan. 2004.

• [5]    P.Zheng, J. Zhao, J. Han, J. Wang, Z. Yao, and R. Liu, “Optimization of the Magnetic Pole Shape of a Permanent-Magnet Synchronous Motor”, in IEEE Trans. Magn.,vol. 43, no. 6, June 2007.

• [6]    C. Hwang, P. Li, F. C. Chuang, C. T. Liu, and K. H. Huang, “Optimization for Reduction of Torque Ripple in an Axial Flux Permanent Magnet Machine”, in IEEE Trans. Magn.,vol. 45, No. 3, march 2009.

• [7]    S. I. Kim, J. Y. Lee, Y. K. Kim, J. P. Hong, Y. Hur and Y. H. Jung, “Optimization for Reduction of Torque Ripple in Interior Permanent Magnet Motor by Using the Taguchi Method”, in IEEE Trans. Magn.,vol. 41, no. 5, may 2005.

• [8]    Y. Y. ang, X. Wang, R. Zhang, T. Ding, and R. Tang, “The optimization of pole arc coefficient to reduce cogging torque in surface-mounted permanent magnet motors”, in IEEE Trans. Magn., vol. 42, no. 4, April 2006.

• [9]    G. H. Kang, Y. D. Son, G. T. Kim, and J. Hur, “A novel cogging torque reduction method for interior-type permanent-magnet motor”, in IEEE Trans on Industry applications., vol. 45, No. 1, Jan/Feb 2009.

• [10]    K. Y. Hwang, S. B. Rhee, B. Y. Yang, B. Kwon, “Rotor pole design in spoke-type brushless dc motor by response surface method”, in IEEE Trans. Magn., vol. 43, no. 4, April 2007.

• [11]    R. Islam, I. Husain, A. Fardoun, and K. McLaughlin, “Permanent - magnet synchronous motor magnet designs with skewing for torque ripple and cogging torque reduction”, in IEEE Trans on Industry applications., vol. 45, no. 1, Jan/Feb 2009.

• [12]    S. W. Youn, J. J. Lee, H. S. Yoon, and C. S. Koh, “A new cogging-free permanent-magnet linear motor”, in IEEE Trans. Magn., vol. 44, no. 7, July 2008.

• [13]    S. W. Youn, J. J. Lee, H. S. Yoon, and C. S. Koh, “Robust design of a spindle motor: a case study”, in reliability engineering and system safety 75 (2002) 313-319.

• [14]    N. Bianchi and S. Bolognani, “Design optimisation of electric motors by genetic algorithms,” IEE Proc.—Electr. Power Appl., vol. 145, no. 5, pp. 475–483, Sep. 1998.

• [15]    M. Lukaniszyn, M. JagieLa, and R. Wrobel, “Optimization of permanent magnet shape for minimum cogging torque using a genetic algorithm,” IEEE Trans. Magn., vol. 40, no. 2, pp.1228–1231, Mar. 2004.

• [16]    J. T. Li, Z. J. Liu, M. A. Jabbar, and X. K. Gao, “Design optimization for cogging torque minimization using response surface methodology,” IEEE Trans. Magn., vol. 40, no. 2, pp. 1176–1179, Mar. 2004.

• [17]    T. Ohnishi and N. Takahashi, “Optimal design of efficient IPM motor using finite element method,” IEEE Trans. Magn., vol. 36, no. 5, pp. 3537–3539, Sep. 2000.

  
  
  

  Sayyed Asghar Gholamian was born in Babolsar, Iran, in 1976. He received a B.Sc. degree in electrical engineering     from    K.N.Toosi

  University of Technology, Tehran, Iran in 1999 and a M.Sc. degree in electric power engineering (electrical

  machines) from university of Mazandaran, Babol, Iran in 2001. He also received the PhD degree in electrical engineering from K.N.Toosi University of Technology, Tehran, Iran in 2008. He is currently an assistant professor in the department of Electrical Engineering at the Babol Noshirvani University of Technology, Babol, Iran. His research interests include design, simulation, modeling and control of electrical machines.