Colonial Competitive Optimization Sliding Mode Controller with Application to Robot Manipulator

Published Online June 2013 in MECS

Senior Researcher at Research and Development Unit, Sanatkadehe Sabze Pasargad Company, (S.S.P. Co), Shiraz, Iran,

• I.    Introduction and Motivation

SMC is one of the most powerful nonlinear robust controllers used in a variety of applications. It is composed of variable structure with the switching output in a distinct state space [1]. Stability and robustness are two main characteristics of this controller.

However, the drawback for this controller is the chattering phenomenon caused by a noisy environment. To overcome this problem several works were proposed [2-3].To illustrate, the consideration of boundary layer near the switching surface was proposed [4]. One of the best techniques to overcome this challenge is the use of soft computing (SC) methods in classical controller switch leads to introduction of intelligent agents integrated with SMC algorithm [5-9, 26-31].

Soft Computing (SC) was introduced by Prof. Lotfi Zadeh as one of the intelligent technologies and has been applied to variety of problems widely. SC technologies consist of neural networks (NNs), fuzzy logic (FL), and probabilistic reasoning (PR) which includes belief networks, evolutionary computation (EC), chaos theory, and parts of learning theory. These patterns imitate human intelligence and smart optimization mechanisms detected in the nature [10, 11].The implementation of SC algorithms in SMC can provide good trajectory performance which can be conducted by well tuning the controller’s parameters [12].

In this paper we apply a colonial competitive algorithm (CCA) [13-14] in designing an optimal SMC. A socio-political competition among the empires serves as the main strategy in CCA for achieving the optimum result in SMC parameters. Similar to other evolutionary algorithms that use an initial population, CCA begins with initial empires. Each empire consists of individual countries. There are two different types of countries: colonies and imperialists. CCA constitutes a colonial competition among the empires in which the weakest empires collapse. The competitions continue to a point so that there would be only one empire with its colonies while the colonies have the same cost as the imperialist. In designing SMC for robot manipulator, CCA is utilized in optimizing the SMC parameters. The controller achieved from CCA is compared with the typical trial and error method.

Robotic mechanisms are a set of rigid bodies known as links connected by joints. The proposed controller is applied to PUMA-560 which is an academic and industrial 6 DOF serial robot manipulator. Dynamic parameters of PUMA 560 robot manipulator have been identified and written [15].

As this paper follows, section II provides a brief description about the robot model of robot manipulator, studies classical Sliding Mode Controller (SMC) and gives an introduction about Colonial Competitive Algorithm (CCA), section III studies the proposed methodology of tuning SMC with socio-political Imperialist Competitive Algorithm (ICA), section IV demonstrates simulation results, and finally section V investigates the conclusion.

• II.    Theory

Dynamic Formulation of robot manipulator: The dynamical equation for an n-link robot manipulator is as following [6, 8, 9, 17, 22, 23, 26-31]:

M (q) q + C (q,i))q + G (q) +t d=T (1)

Where, M (q) 6 Rn x n is symmetric and positive inertia matrix, and q ,q,q6 Rn represent the position, velocity, and angular acceleration of the robot joint, respectively. C (q , q) 6 Rn xn is the matrix of Coriolis and Centrifugal forces.The matrix of G (q ) 6 Rn x 1 is the gravity vector, 6 is the bounded disturbance vector and 6 is the control input vector.

Any changes in nonlinear parameters such as Coriolis and Centrifugal functions can cause changes in velocities and subsequently in position. In this case, the robot dynamic equation known as configuration space can be demonstrated as:

т =M (q) q + B (q). [qq] +C(q).[q2 ]+G(q) (2)

Where, B (q) Є R ^{n x n (n-1)/2} indicates matrix of Coriolis torque and C (q) Є R ^n×n displays matrix of Centrifugal torques.

Some researches perform either the summation of Lagrange’s formulation or the Gibbs-Alembert formulation to acquire the kinetic energy matrix and gravity vector which can be used to derive the dynamic modeling of the robot manipulators [2, 3, 8-16]:

q - M ((q). [t - [B(q).[qq] + (3) C(q). [q2] + G(q)]}

This technique is very effective since the nonlinear and coupled robot manipulator dynamics are replaced by a linear and decoupled second order system. In this paperfirst 3 degrees of freedom PUMA 560 robot manipulator is modeled and discussed.

Classical sliding mode controller for robot manipulator: sliding mode controller description, problem statement and some solutions was presented in literature [15-21, 26-31].We can write the control law of SMC for six degrees of freedom PUMA-560 classical robot manipulator as [8]:

τ = τ sat+τ equ

The discontinuous part of total torque so called saturation component (τ sat) and computed as:

Where S is the time varying sliding surface, φ is the boundary layer thickness, sat () is the saturation function and the k is the switching gain which is positive and determined by:

S = е + Л * e + (Л/2)2 Jedt

(e=q desired -q actual )

e represents error rate,A is a coefficient and sa^s/ф) can be written as:

I 0i

if jSij > р,

i f j s ij < р,

And the model-based component (t _equ) represents the nominal dynamics of systems which can be calculated as follows:

Tequ= [ M-((B+C+G) + S ]*M

Where, S is the derivation of the sliding surface and will be written as:

S = ё + л * e + (I) * e

(θ=q desired )

The expression for control output by replacing (5) and (8) in (4) can be written as:

t= [M-((B + C + G) + S] *M+            (10)

к. sa t( s / р )

Colonial Competitive Algorithm (CCA): Imperialism is the standpoint of developing power and control by a government to further increase its own territory. A country may rule others out by either direct control or less obvious means such as a control of markets for goods or raw materials which is so called neocolonialism [24]. Colonial Competitive Algorithm (CCA) is a new global heuristic and initiative search that utilizes imperialism and imperialistic contest process as an origin of inspiration. E. Atashpaz- Gargari and C. Lucas presented the hierarchical steps of CCA as following [13, 14]:

• 1)    Select some random points on the function and initialize the empires.

• 2)    Move the colonies toward their relevant imperialist (Assimilating).

• 3)    If there is a colony in an empire which has lower cost than that of imperialist, exchange the positions of that colony and the imperialist.

• 4)    Compute the total cost of all empires (Related to the power of both imperialist and its colonies).

• 5)    Pick the weakest colony (colonies) from the weakest empire and give it (them) to the empire that has the most likelihood to possess it (Imperialistic competition).

• 6)    Eliminate the powerless empires.

• 7)    If there is just one empire, stop, if not go to 2.

The procedure of process begins with an initial population. Any individual of the population is called a country. Some of the best countries in the population are chosen to be the imperialist states, and all the other countries constitute the colonies of these imperialists. All the colonies of initial population are apportioned among the imperialists on the basis of their power which are contrarily in harmony with their cost and begin moving toward their related imperialist country. This act of moving is an easy pattern of assimilation action that was investigated by some imperialist states [25] which depicts in Figure 1.

Fig. 1: Motion of Colonies toward their relevant imperialist colonies randomly search around the imperialist. In our implementation β and γ are 2 and π/4(Rad) respectively.

The total power of an empire is the aggregate of power of the imperialist country and the power of its colonies. Any empire that is not able to prosper in imperialist competition and cannot enhance its power or at least prevent diminishing its power will be removed. The imperialistic competition will progressively yield a growth in the power of great empires and a reduction in the power of weaker ones. Feeble empires will misplace their power gradually and eventually they will collapse.

This act of moving of colonies toward their related imperialists along with competition among empires and also breakdown and collapse mechanism will expectantly bring about all the countries to converge to one empire in the world and all the other countries will be its colonies. In this perfect new world colonies have the same position and similar power as the imperialist.

• III.    Methodology

The output of an ideal SMC has some defined characteristics such as having a precise tracking trajectory, stability, robustness, resistivity against the perturbations, least changes to the dynamic parameters, and lack of any chattering phenomenon in the torque. The standard approach to SMC is based on formulation (10).

Luanda (λ)in formulations (6), (9) and (K) in formulation (10) are coefficients which have the prominent impact on discontinuous portion (t _sat). The saturation function (sat(S)) performs the switching procedure. External disturbances influence on the tracking trajectories, error rate, and torque which result in chattering phenomenon. These high oscillations with a small range of motion exist in all systems. In order to achieve a desirable performance by SMC, it is required to tune the two parameters (λ) and (K).

In this paper, the applied methodology chooses the best values for these deterministic coefficients by utilizing the colonial competitive algorithm (CCA). This algorithm optimizes the parameters (λ and K) in order to determine the appropriate values for them. In ICA algorithm, the integral absolute error is used in cost function to calculate the minimum cost function for each decade. The ICA algorithm is applied to SMC by thirty initial countries and five initial imperialist countries.

The competition process can be reviewed in the Figure.2, where the mean and minimum costs of all imperialists versus iteration are depicted. Parameters of SMC obtained by CCA and typical trial and error methods are demonstrated in Table 1.

In this movement, θ and x are random numbers with uniform distribution, and d is the distance between the colony and the imperialist. X ~ U (0, β×d) θ ~ U (-γ, γ) β and γ are arbitrary numbers that adjust the area that

Table 1: The value of parameters for ICA-SMC and SMC

Parameters	ICA-SMC	Typical SMC
Luanda (1st link)	8.0897	5
Luanda (2nd link)	5.5722	7
Luanda (3rd link)	9.0268	5
K (1st link)	43.0758	14
K (2nd link)	63.1662	27
K (3rd link)	38.3783	13

Minimum Cost

662.9

662.8

662.7

662.6

662.5

Best Cost

Mean Cost

0      10     20     30     40     50

• IV.    Simulation Results:

Optimal sliding mode controller using colonial competitive Algorithm (ICA-SMC) and typical trial and error sliding mode controller (SMC) were examined for step response trajectories. In this simulation the first, second, and third joints move from initial point to destination position considering with and without external disturbances. The simulations were performed in MATLAB/SIMULINK. The comparisons were accomplished on indices namely, tracking trajectory performance and chattering rejection or robustness (Disturbance rejection).

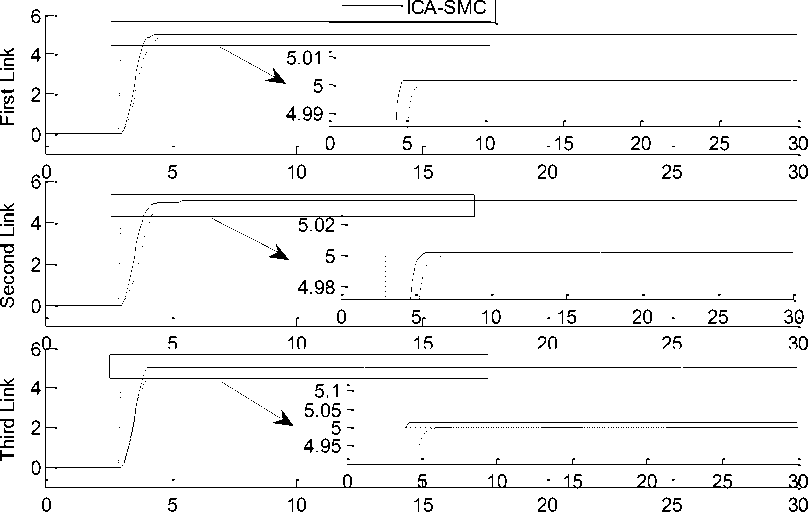
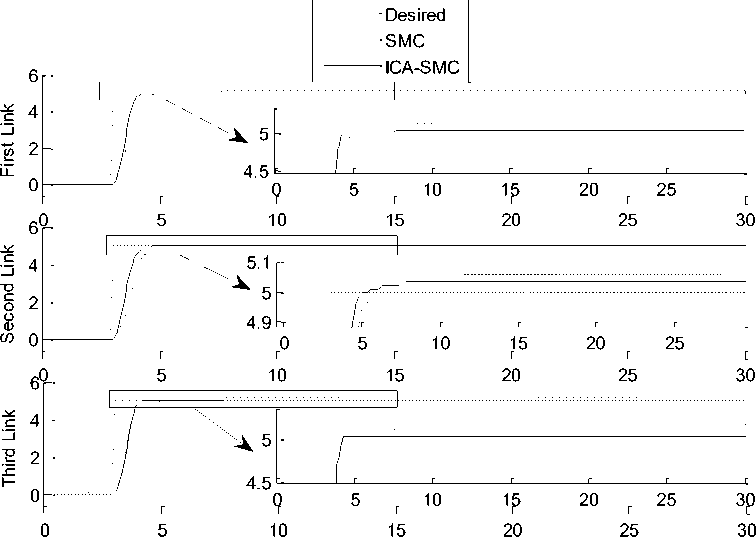
Tracking Performances: As it is obvious in Figure 3, proposed ICA-SMC and typical SMC have similar tracking performance but ICA-SMC has better settling time in every three links while these is no external disturbances. In second step of examination an unknown output disturbance is applied to system. The results in Figure.4 display that the proposed ICA-SMC is able to reject the external disturbances and its tracking is stable. The noise amplitude is equal to 50% of input amplitude and it was exerted simultaneously at the beginning of the process.

Decade

Fig. 2: Mean and minimum cost of all imperialists versus iteration

Desired

SMC

Time

Fig. 3: Step Response of ICA-SMC and SMC for first, second and third link trajectory without external disturbance

Time

Fig. 4: Step Response of ICA-SMC and SMC for first, second and third link trajectory with external disturbance

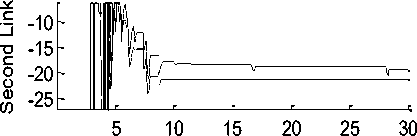
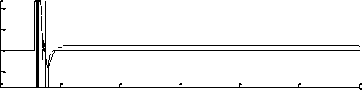
Chattering rejection and robustness: Both SMC and ICA-SMC have similar torque trend when there is no noise (Figure.5).As it was declared, a white noise as an external noise was exerted to system to study the disturbance rejection of it. The results are shown in Figure.6. SMC has oscillation tracking at the presence of disturbances which causes instability and chattering phenomenon while the proposed ICA-SMC displays smoother trend and better performance because it has no chattering phenomenon in its torque and has a stable procedure.

-5 Pq

-10 и

-15t___

SMC

ICA-SMC

0     5    10    15    20    25    30

~ 2

2 -2

'll -4

SMC

ICA-SMC

5     10     15     20     25     30

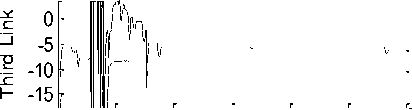
5    10    15    20    25    30

-5

-10

-15

Time

Fig. 6: Torque trend and chattering rejection test to investigate the robustness for all links

5     10     15     20     25     30

0      5     10     15     20     25     30

Time

Fig. 5: Torque Profiles without External Disturbances for all links

• V.    Conclusion:

This paper provides a novel approach in designing an optimal SMC by Imperialist Competitive algorithm applied to PUMA 560 industrial robot manipulator. This new heuristic search tunes the sliding surface slope and the switching gain of the saturation torque in SMC framework for the best output determined in cost function. The cost function calculates all possible responses with the minimum error rate and then chooses the best answer. Simulation results verify that the suggested socio political ICA-SMC considerably lessens the chattering phenomena rather than typical SMC because ICA has optimized and well-tuned SMC’s parameters to obtain the best performance. Subsequently the best possible tracking trajectory is acquired. The proposed ICA-SMC has robustness and stability to external disturbances. Moreover it has smoother torque and trajectory without any high oscillation movements (chattering).