Color Image Segmentation Using Level Set Method With Initialization Mask in Multiple Color Spaces

Image segmentation is one of the key processes in the areas of image analysis, image understanding, computer vision and system identification. The level set method (LSM) is originated in the area of fluid dynamics, for computing the solution to fluid interface problems[1], by Stanley Osher, and James Albert Sethian. Caselles[2] and Malladi[3] developed the level set in vision and image segmentation. After that, there are major milestones in the improvement of level set, such as stereo reconstruction[4], active regions and grouping[5], mumford-shah variant[6,7], shape priors[8], computational geometry [9], and shape recovery[10]. In this article we discuss recent variants and extensions to level set approach, and also give a

• * Corresponding author.

2.    The Improvement of Chan-Vese Model

user’s guide to the level set dictionary and technology. The level set method, as one of the state-of-art algorithms, whose excellence is that one can perform numerical computations involving curves and surfaces on a fixed Cartesian grid without having to parameterize these objects, is a numerical technique for tracking interfaces and shapes of an object. Also, it is very easy to track shapes with topological changes by the level set method. But it would be quite hard to describe this transformation numerically by parameterizing the boundary of the shape and following its evolution. All these advantages of the level set method make it a powerful tool for modeling time-varying objects. Moreover, a number of level set data structures have been developed to facilitate the use of the level set method in computer applications. So far, it has become popular in many disciplines, such as image processing, computer graphics, optimization, computer vision, computational geometry, computational fluid dynamics, and biomedical imaging. Vector image segmentation algorithms have been commonly evaluated in RGB color space. Here we present the common color spaces used in the image processing field. And then we give comparatively study the performance of color image segmentation using the optimized Chan-Vese model with initialization mask in multiple color spaces.

The Mumford-Shah framework [11] is a region-driven case of Level Sets. It originally aims at partitioning the image into (multiple) classes according to a minimal length curve and reconstructing the noisy signal in each class. Mumford and Shah suggested minimizing the following energy functional:

E ( C , u ) = α ∫ ( u - g ) ² dA + β ∫ тс । ∇ u | ² dA + γ Η ^{n - 1} ( C ) (1)

Here g is the observed data defined on an open bounded set Ω⊂ Rⁿ and u with discontinuities only along C , represents the piecewise smooth approximation to g on Ω \ C . Η ^{n - 1} denotes the n - 1 dimensional Hausdorff measure and the parameters α , β and γ are positive weights, which control the balance between data fit, regularization of the reconstruction u on Ω \ C , and the length of contour C respectively, where C is smooth, closed segmenting curve.

Let us consider the discrete binary case and the fact that the reconstructed signal is piecewise constant

E ( C , µ _in , µ _out ) = α ( g - µ _in ) ² d ω

^Ω in

+β∫∫  (g-µout)2dω+γ∫ | C′ | dc

Ω out

Here the objective is to reconstruct the image, using the mean values µ , µ for the inner and the outer region respectively. This is quite simplistic model, quite often the means are not a good indicator for the region statistics with absence of use on the edges, boundary information.

Chan-Vese Model is a particular case of the Mumford-Shah model in a simplified form [6]. It can detect objects without sharp edges, and cognitive contours with robustness to noise. Also, this model can be applied to multiple objects segmentation [7] and vector image [12]. Here we propose a novel initial method to optimize Chan-Vese model, and carry out comparative study of partition in multiple color spaces. Masking grids as initialization mask in Cartesian coordinate plane are first created by either the user or the built-in mask creation function using mathematical morphology, where the user defined mask can only be logical or binary. The shapes of cells on grids can be various, such as square, rectangle, octagon, disk, and diamond. They have some influences on segmentation results. The mathematical formation of masking grids is:

ucS = F ( x, У )

Assume that the cell shape on grids is disk, we can get

u

cs

= <

1,

. 0,

( x - x ) ² + ( y - y j² <  r² others

Where r is a positive constant. ( x₍ , y ) and ( x , y ) are the centers of the cells with certain interval distributed on the grids and the element’s positions in the neighborhood of the cell’s center respectively. Then initial values are generated from masking grids according to the Euclidean distance transform of the binary image. And initial contour is simultaneously specified manually for convenient observation in experimental results. The initial values for the input image derived from masking grids are computed from the following formula:

u0 = ucs - 0.5 + d (ucs ) - d (1 - ucs )

Here d(•) denotes the Euclidean distance transform of the binary image, whose value is a number that is the distance between that pixel and the nearest nonzero pixel.

Chan and Sandberg in [12] have extended the scalar C-V model to the vector case. Assume that C is the evolving curve that is the boundary between these two regions, and u₀₁ is the i th channel of an image on Q , with i = 1, ••• , N channels. Suppose that c + = ( c + , ••• , c N ) and c - = ( c 1 - , ••• , c ^ ) are two unknown constant vectors. Each channel of color images would contain the same image with some differences relevant to different wavelengths at which the image was capture taken. The minimized energy controls the balance of the contours in the image, with the fitting of u , averaged over all the channels. Minimizing the energy functional with respect to the constants c + , c - , i = 1,2, • • •, N , the extension of the C-V model is:

F ( c ⁺ , c , ф ) = ц- Length ( C )

+Ц ;1 E N л; uo,i (x, у ) - c+ Г dxdy

⁺L. ;1 E N ^x t u o, . ( x , y ) - c -1² dxdy

Here z + >  0 and X. >  0 are parameters for each channel. As in each channel, this model seeks the best approximation taking only two values, namely the constant vectors c ⁺ and c - . Rewriting it in level set form for each channel i = 1,2, • • •, N , we obtain

F (c+, c " ,ф) = ц£ 8 (ф( x, y ))^ф( x, y )| dxdy

+£ ;1 £ NiX u 0,‘ (x, y)-c Г H (ф(x, y)) dxdy                                               (7)

+£ ^ ^N Х lu0,1 (x, У ) - ci Г (1 - H (ф(x, У ))) dxdy

And c + and c. are:

c +

— c i

Juo i (x, у)H (ф(x, У)) dxdy £ H (ф( x, y)) dxdy

£ u o, i ( x, y ) ( 1 — H ( ф ( x, y ) ) ) dxdy £( 1 ^{— H} ( ^ф ( ^x , У ) ) ) dxdy

Here, The parameters ц and Я ⁺’"=( ^ ’", Л +^{, —} ,•••, Л + ’ j are parameters to tuning the object detector sensitivity. ц is the weight for the length term, while the coefficients X are the weights for the error term. Large ц or small X are necessary for the model to filter high frequency noise. Likewise, larger coefficients X are necessary to detect objects with fine detail. 8 ( • ) and H ( • ) are the Heaviside and Delta functions respectively.

3.    Implementation and Results

The main process of the Chan-Vese model(C-V model) with initialization mask in multiple color spaces described in detail in this paper is illustrated in Fig.1. The improvement of this algorithm for color image segmentation mostly lies in built-in masking grids and effects of different color space on partition results.

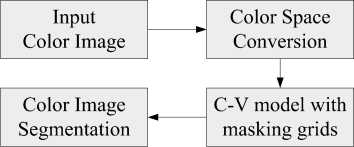
Fig.1 Overview of Chan-Vese model with masking grids for color segmentation

(a) masking grid

(b) initialization value

Fig.2 the improvement of initialization method

In order to test the performance of the proposed method, we ran a large number of natural images and artificial images through the Matlab codes. The images we used were chosen as they contained areas of various performance indicators, which served to evaluate the optimized Chan-Vese algorithm in multiple color models. Since there is no objective indicator to measure the segmentation maps qualitatively, the performance indicators for test images are introduced here: 1) The waterlily and background are clear and distinct; 2) The shape of each area is recognizable; 3) The numbers of these areas are correctly countable. As well as visually comparing the resulting images, we take performance indicators for each image as an objective measure of performance. In this experiment, cell shape is diamond, which is different from circle as normal initialization. After dilating masking grids and Euclidean distance calculation, the initialization value is observed, as show in Figure 2. Figure 3 demonstrates the visual effects of the improved Chan-Vese algorithm in different color spaces. The results of test image changes little, which illustrates the optimized Chan-Vese algorithm has good adaptability in RGB, CIE XYZ, and YCbCr color spaces. Through experimental tests with a set of images, performance analysis with evaluation indexes shows that best results by the Chan-Vese color image segmentation came from RGB, CIE XYZ, and YCbCr color spaces. However, the refined Chan-Vese algorithm did not show good performance in CIE L*a*b*, and h1h2h3 color space.

(a) Original image            (b) RGB

(c) XYZ              (d) CIE L*a*b*

(e) YCbCr           (f) YIQ(NTSC)

(g) h1h2h3

(h) HSV

Fig.3 Segmentation results of the C-V Algorithm using initialization mask in several color spaces

4.    Conclusion

This paper reported to explain on which color space the improved Chan-Vese model for color image segmentation is better. The experimental results prove the effectiveness of the optimized Chan-Vese algorithm in RGB, CIE XYZ, and YCbCr color spaces, while the other color spaces, namely CIE L*a*b*, and h1h2h3, yield poor effects. Moreover, the refined Chan-Vese model produces faster and better segmentation results with robustness to noise. Notice that the results using RGB are generally better than results obtained from other color spaces. However, the difference in quality between these color spaces, i.e. RGB, CIE XYZ, and YCbCr, is small. The decision of image segmentation map quality with performance indicators introduced in this paper is quite subjective and relative. This kind of intuitive performance indicator are helpful to decide better segmentation map with certain rules, but objective methodology of measuring the quality of image segmentation is necessary to improve the reliability of the comparison. Therefore, better results can be acquired by appropriately selecting some segmentation algorithm in proper color space.