Combinatorial optimization in foundry production planning

Production capacity optimization. One of the actual problems in modern industry is production capacity optimization under irregular orders from numerous partners. Along with the mass serial production these orders may have small serial or single nature. The majority of orders are irregular, i. e. they cannot be planned beforehand but nevertheless they are profitable enough or the enterprise. It requires solving production scheduling problems many times in casual points of time.

So it is necessary to have means for including new small orders in capacity intervals of existing mass serial ones. Moreover, it is necessary to consider time of equipment revamping for small serial order since it takes significantly more part of execution time than in mass serial production.

Existing of small serial and single orders requires practically permanent process of production capacity planning. Construction of production capacity program for industrial enterprise and its subdivisions is laborious and logically intricate problem. Consider it by the example of foundry practice. Below we design an optimization model for production capacity and apply combinatorial methods to solve it.

Pseudo-Boolean optimization problems. Unconstrained pseudo-Boolean optimization is an issue studied enough by now. Algorithms that have been designed and investigated in the area of unconstrained pseudo-Boolean optimization are applied successfully for solving various problems. Particularly, they are local optimization methods [1–3] and stochastic and regular algorithms based on local search for special function classes [4–6]. Moreover, there are a number of algorithms for functions optimization given in explicit form: Hammer’s basic algorithm that was introduced in [7] and simplified in [8]; algorithms for optimization of quadratic functions [9–11], etc. Universal optimization methods are also used successfully: genetic algorithms, simulated annealing, tabu search [12; 13].

If there are constraints on the binary variables, one of the ways to take into account it as is well known is construction and optimization of a generalized penalty function. Shortcoming of this approach is existence of a large number of local optima of the generalized function what will be shown below. If an accessible region is a connected one then this issue could be partly eliminated, for example, by using local search with a stronger system of neighborhoods. Extension of search neighborhood reduces the number of local optima which locate mainly not far one from another in this case. If an accessible region is unconnected then using penalty functions and unconstrained optimization methods get complicated because the accessible region is usually too small with the respect to optimization space. That makes difficult searching a feasible solution.

In this work heuristic procedures of boundary point search are considered for a constrained pseudo-Boolean optimization problem. Experimental investigation of the algorithms are described, recommendations for their apply are given.

Search algorithms for pseudo-Boolean optimization. Basic definitions. Consider some definitions that are necessary for describing optimization algorithm work [14].

A pseudo-Boolean function is called a real function of binary variables: f : B ₂ ⁿ ^ R 1 , where B ₂ = { 0,1 } , B 2 = B ₂ x B ₂ x Л x B ₂.

Points X ’, X ² e B ₂ ⁿ are called k-neighboring points if they differ in k coordinate value, k = 1, n . 1-neighboring points are called simply n eig hboring.

The set O k ( X ), k = 0, n , of all point of B ₂ ⁿ , that are k -neighboring to a point X , is called a k-th level of the point X .

A point set W ( X °, X l ) = { X °, X 1, K , X l } c B n is called a path between points X ⁰ and X l if for V i = 1,..., l the point X i is a neighboring to X i ^{- 1}.

A set A c B n is called a connected set if for V X ⁰, X^l e A the path W ( X ⁰, X l ) c A exists.

A point X * e B n , for which f ( X * ) <  f ( X ), V X e O 1 ( X * ), is called a local minimum of pseudo-Boolean function f.

A pseudo-Boolean function that has an unique local minimum is called an unimodal on B ₂ ⁿ function.

An unimodal function f is called monotonic on B ₂ ⁿ if V X k e O k ( X •), k = 1, n : f ( X k -1 ) <  f ( X k ), V X k ' e O_t _1 ( X *) n O J X k ) .

Problem statement. Consider the problem of the following form

C ( X ) ^ max , (1) where C ( X ) is a monotonically increasing from X ⁰ pseudoBoolean function, S c B 2 is a certain subspace of the binary variable space; it is determined by a given constraint system, for example:

A ( x ) <  H j , j = 1 m . (2)

In the general case a set of feasible solutions S is an unconnected set.

One of ways to take into account constraints in conditional problems is construction a generalized penalty function that is solved by known search methods: local search, genetic algorithms, simulated annealing, etc. Shortcoming of this approach is loss of the monotonicity property for an object function. By addition of even simple (for example, linear) constraints the generalized function becomes a polymodal nonmonotonic function with exponential number of local maxima.

Properties of a feasible set. A point у _e A is a boundary point of the set A if there exist X e O 1 ( Y ) for which X £ A .

A point Y e O i ( X ⁰) n A is called a limiting point of the set A with the basic point X ⁰ e A if for V X e O 1 ( Y )I O_{i + 1}( X ⁰) X £ A holds.

A constraint that determines a subspace of the binary variable space is called active if the optimal solution of the conditional problem does not coincide with the optimal solution of the appropriate problem without taking the constraint into account.

If the object function is a monotonic unimodal function and the constraint is active then the optimal solution of the problem (1) is a point that belongs to the subset of limiting points of the feasible set S with the basic point X ⁰ in which the object function takes the lowest value:

C ( X °) = min C ( X ).

X e B n

Properties of feasible sets are considered detailed in [15; 16].

Heuristic algorithms for boundery point search. For any heuristic of boundery point search we will consider a pair of algorithms – primary and dual. A primary algorithm starts search from the feasible area and moves in a path of increasing of the objective function until it finds a limiting point of feasible area. Otherwise, a dual algorithm keeps search in the unfeasible area in a path of decreasing of the objective function until it finds some available solution.

Total scheme of primary search algorithm:

• 1.    Put X 1 = X ⁰, i = 1.

• 2.    In accordance with a rule we choose X i _{+ 1} e O i ( X ⁰) n O 1 ( X; ) n S . If there are no such point then go to 3; else i = i + 1 and repeat the step.

• 3.    X opt = X i +1 .

Total scheme of dual search algorithm:

• 1.    Put X 1 e O n ( X °), i = 1.

• 2.    In accordance with a rule we choose X i _{+ 1} e O_n - i ( X ⁰) n O 1 ( X i ). If X i _{+ 1} e S then go to 3; else i = i + 1 and repeat the step.

• 3.    X opt = X i +1 .

From these schemes we can see that a primary algorithm finds a limiting point of the feasible area, but a dual algorithm finds a boundary point which may be not a limiting one. So a primary algorithm finds a better solution then dual in most cases for problems with a connected set of feasible solutions. If we will use a primary algorithm for a problem with a unconnected feasible area then solution received in result may be far from the optimal because feasible and unfeasible solutions will rotate in a path of increasing of the objective function. For these cases a dual algorithm is more usefull, because this rotation does not play any role for it. For improving the solution that given by the dual algorithm, it is recommends to apply the corresponding primary algorithm. Such improving is very significant in practice.

Boundary point search algorithms considered below differs by only a rule of choise of a next point in step 2 of the total schemes.

Search rules. Rule 1. Random search of boundary points (RSB).

A point Xi+1 is chosen by random way Each point in the next step can be chosen with equal probabilities. For real-world problems these probabilities can be not equal but they are calculated in the basis of problem specific before search starts.

Rule 2. Greedy algorithm.

A point X; +1 is chosen acordance with the condition

X( X. ,) = max X( X’ ),

j where X1 e O.(X0) n O1(X) n S for a primary algorithm and XJ e On - (X 0) n O1( X) for a dual one.

The function λ( X ) is chosen from the specific problem, for example:

• -    the objective function X( X ) = C ( X );

• -    specific value X( X ) = C ( X )/ A ( X ) (for only constraint) and so on.

Rule 3. Adaptive random search of boundary points (ARSB).

A point X . +1 is chosen by random way in accordance with a probability vector

P = (p}, P2,-, pJ), where J is the number of points from which choice is made.

p j

λ( X^j )

j , ^J = ¹ J i E ^( X^l )

i =1

where X^J e O . (X 0 ) n O 1 ( X . ) n S for a primary algorithm and X^J e O n - ( X 0 ) n O 1 ( X . ) for a dual one.

ARSB is an addition to the greedy algorithm.

Rule 4. Modificated random search of boundary points (MRSB).

A point X ,. _{+ 1} is chosen in accordance with the condition

Z( X i+1) = max Z( Xr), r where Xr are points chosen in accordance with the rule 1, r = 1, R ; R is an algorithm parameter.

A greedy algorithm is a regular algorithm [17], so it finds equivalent solutions under restart from a certain point. Other algorithms can be started several times and the best solution can be selected from the found solutions. An average run time of a greedy algorithm and ARSB is significant larger than for others because they look over all points of the next level in each step in distinction from RSB and MRSB which looks over only one and R points correspondingly in each step in a dual scheme.

Further we consider applying the described algorithms for one of real-world problems with large dimension and unconnected set of feasible solutions.

Foundry branches production capacity optimization. Production of different kinds is produces in foundry branches (FB). There is specialization in every FB by a kind of production which can be produced by its foundry machines (FM). There is a quantity of orders for production. To each order there corresponds the volume, a kind of production and term of performance. The kind of production is characterized by productivity for change (only 3 changes in day). Replacement made on FM production demands its recustomizing borrowing one change. It is necessary to load thus FB capacities the orders were carried out all, production was made in more regular intervals in time, and the number of recustomizings of FM equipment was minimal.

Input data:

I is a number of days for planning;

• J is a number of FB;

K j is a number of FM in J -th FB, J = 1, J ;

L is a number of orders for production that produces on FM (and corresponding number of production kinds);

V_l is pro du ctivity of l -th kind of production for change on FM, l = 1, £ ;

T_l is term of perfor m ance of l -th order (for production of l -th kind) on FM, l = 1, L ;

W_l is vo lume of l -th order (for production of l -th kind) on FM, l = 1, L ;

z_jl characterizes specialization of FB:

• 1,    FM of j -th FB can make production of l -th kind, 0, otherwise;

  
  
  

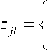
α is the factor of rigidity of restriction on demand of uniformity of production a days, 0 <  a <  1.

Variables:

For the model construction introduce the following binary variables:

Y = { У_ци } e B П ,

X = { x_tikl } e B П , where B ₂ = { 0,1 } , B ₂ ⁿ = B ₂ x B ₂ x Лх B ₂ is a set of binary variables.

• 1,    production of l -th kind is made

y_ijfcl = { in i —th day on k -th FM of J -th FB,

0, otherwise;

xijkl

1, production of l -th kind is started to make = <  in i -th day on k -th FM of J -th FB,

0, otherwise;

Total dimension of a binary vector Y (and X) is n = I ■ L -JKr j =1

Remarks:

• 1.    J ^ y .Jkl V i , J , k , l .

• 2.    х _ци = У_ци ■ (1 - У . -1, Jkl ) V i , J , k , l ( y 0J _k l = 0 V j , k , l ). (3) Optimization model:

• 1.    The objective function and the main constraints:

C ( X ) ^ min ,                (4)

AXY ) >  W l , l = 1, L ,                (5)

A^(Y ) >  a ■ WI , i = 1, I , a e (0,1), W' =^W_t Il , (6) l =1

where

IJ ^K j LIJ ^K j L

C ( X ) = EEEE x_UH = ЕЕЕЕ у_ци -( 1 - y J ) , i =1 j =1 k =1 l =1              i =1 J =1 k =1 l =1

^T l J ^K j

A'(Y ) = EEE Vl ■ Уу_к1 ■( 2 + Yj ) , i =1 j =1 k =1

J ^K j L

A 2 ( Y ) = EEE V y jl ■ ( 2 + У. -1, Jkl ) , j =1 k =1 l =1

• У 0jkl = 0 ^V j , ^k , ^l .

• 2.    The additional constraints:

E У j _u ^ 1 ( E X ijkl ^ 1), i = 1, 1 , J = 1, J , k = 1, K j , (7) l =1                      l =1

У у_И ⁵ z ji ( х_уи ^ ^zji ), i = 1, I , j = 1, J , k = 1, K , I = 1, L .

Model properties:

• 1.    There are two spaces of binary variables (denote their by B^X and B^Y ) corresponding to vectors X and Y . For each point Y e B Y a unique point X e B^X corresponds, components of which are determined by relation (3). Several points Y e B Y (with different value of constraint function) can correspond to the point X e B^X .

• 2.    The objective function (4) is linear and unimodal monotonic in space B^X with the minimum point X 0 = (0, ...,0). In space B Y the objective function is a quadratic and unimodal nonmonotonic one with a minimum point Y ⁰ = (0,..., 0).

• 3.    The constraint function (5) and (6) in space B^Y are quadratic and unimodal monotonic pseudo-Boolean functions with a minimum point Y ⁰ = (0,..., 0). In space B X the constraint functions unequivocally are not certain.

• 4.    The feasible set in spaces B^X and B^Y is limited from J

• 5.    The feasible set is an unconnected set in general case (in space B^Y ).

above by I - E K j -th level of the minimum point ( X ⁰ and Y ⁰) according to the constraint (7). In space B Y this level corresponds to the case when production is produced on each BM every day.

Thus the problem solution is defined completely by the variables Y , but it does not hold for the variables X . But the objective function from X has good constructive properties so that optimum search on X is more efficient than on Y . As the constraint function (5), (6) from X are not defined, we should find values of these functions from the corresponding point Y . There exist perhaps several such points

X ^ Y Y 2 ,..., Y h .

Not at all points the solution may be feasible but in other not. As the constraint functions are monotonic here then for a certain X we should choose such Y that belongs to the most possible level (with the most values of the functions):

Y = arg  max I E y hki |,

Yh, h =1, HI i, j, k, l      J where Yh = (ylm,...,yUKjL).

One of the algorithms of this transformation is presented below.

Algorithm 1 of transf or mation X to Y :

• 1.    Put N_jk = 0 , j = 1, J , k = 1, K j ; i = 1.

• 2.    For j = 1, J , k = 1, K j , l = 1, L do: if x _w = 1 then N_jt = l .    _    ___ _

• 3.    For j = 1, J , k = 1, K j , l = 1, L do: if N_jk = l then y_ti ki = ¹ else y jkl = ⁰.

• 4.    If i <  I then i = i + 1 and to 2.

At the same time the solution Y received from the found best vector X _opt by this way may corresponds to situation when a quantity of let out production is more higher than the requisite value (it does not contradict to the constructed model but this can influence uniformity of capacities loading which is optimized at the next stage). So when the first stage of search has ended, we should define Y _opt by the rule

X opt ^ Y 1 , Y 2 ,..., Y h ,

• Y p_t=arg  , mm -|e y h I.

p            Y_h : A l ( Y h )> W l , l =1, L ^ i ,“, l j J

In this case the transformation algorithm has some differences from the previous.

Algorithm 2 of transf or mation X to Y :

• 1.    Put N_jk = 0, j = 1,J_ , k = 1, K j .     ____ _

• 2.    For j = 1, J , k = 1, K j , l = 1, L do: if x_jjkl = 1 then N j _k = l .    _    ___ _

• 3.    For j = 1, J , k = 1, K, , l = 1, L do: if N = l and j                                    jk

• 4.    If i <  I then i = i + 1 and to 2.

i = 1.              ____ ______ ____

A 1 ( Y ) <  W then y jkl = ¹.

Here the condition A l ¹ ( Y ) <  W l is added in the step 3, and the step 1a is added also for possibility of this calculation. There is no necessity in this transformation during the search. It is necessary only to determine the result Y _opt .

Optimization algorithms. The dual algorithms RSB, greedy and MRSB have been used for solving the problem. The algorithm ARSB has not been considered for this problem because of its excessive large run time by frequent start. One start of ARSB can very rarely give a solution which is better then the solution given by the greedy algorithm. The start point of search is the point of the unconstraint minimum of the objective function X ⁰ = (0,..., 0). A found solution has been improved by the corresponding primary algorithm.

Moreover, the problem has been solved by the genetic algorithm (GA). To realize GA we have chosen a scheme that effective worked for multiple solving other combinatorial optimization problems.

Results of the experiments shows that the most effective algorithms (by precision and run time) from the considered ones for this problem are the greedy algorithm and MRSB. The other algorithms under hard constraints on the variables do not find any accesible solution at all. It is a sequel of problem specific: a large amount of different constraints and, as a result, a comparative small accesible regin.

The average results of solving 10 problems of month planning capacity loading are presented in the table. The average values of input data:

I = 31, J = 3, K 1 = 12, K 2 = 9, K 3 = 7, L = 36, a = 0,5,

V l e [40,50], W l e [20,25 000].

Herewith the total dimension of the binary vector is n = 31 248.

The number of algorithm starts L has been chosen so that the run time nearly equals to the run time of one start of the greedy algorithm. In this case the run time equals to T « 8 - 10 5 .

MRSB is a more flexible procedure in compare with the greedy algorithm as the first one allows selecting the parameters L and R that influence on algorithm run time and solution precision. The greedy algorithm does not allow that possibility and run time may be overmuch large under high dimensions. What about their efficience, precision of the found solutions differs unessentually under nearly equivalent run time.

The optimization model for foundry production capacity planning is designed. It corresponds to the conditional pseudo-Boolean optimization problem with an unconnected feasible set and it is solved by the series of heuristic search algorithms. The algorithms of boundary point search show high efficiency for solving the pseudo-Boolean optimization problem with an unconnected accessible region. The most efficient algorithms for the considered problem are the dual algorithms MRSB and greedy one.