Comparative Analysis of ANN based Intelligent Controllers for Three Tank System

Published Online March 2016 in MECS

Three tank liquid level control system plays a significant role in process industries such as iron and steel, petroleum, chemicals etc., and fluid handling systems. In most of the industries, for controlling linear and negligible delay processes PID controllers are used. But, level control system is a time-varying, large lag and nonlinear complex control system and it is difficult to control with conventional PID controller. This is due to the fact that efficient control of nonlinear, complex and vague systems cannot be done using conventional controllers. Hence in this paper we proposed the design of three intelligent controllers namely ANN based model predictive, model reference controllers and NARMA-L2 for this nonlinear control system. The controllers design and simulation is done using MATLAB/SIMULINK software.

• II.    Mathematical Model of Three Tank System

A three tank level process used in industrial applications is shown in Fig.1 [1]. Here q: Liquid inflow rate initially; q0: Liquid outflow rate finally; h1, h2, h3: Liquid height in three tanks respectively; A1, A2, A3:

Cross sectional area of three tanks respectively.

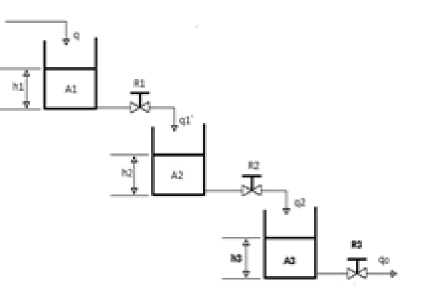
Fig.1. Three tank system

For tank-1:

q - q i = A

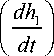
For tank-2:

For tank-3:

q 2   q 3    A 3

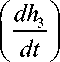
Firstly, ANN is trained to represent the process forward dynamics. The prediction error yp-ym between the plant output and the neural network output is the ANN training signal [5] as shown in Fig.2. Fig.3 shows NN process model representation which predicts process future data based on previous data.

And AR = T; AR = T; AR = T

By solving equations (1), (2) and (3), the transfer function of the above three tank system is

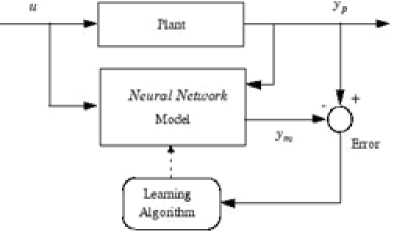
Fig.2. System identification of MPC

The transfer function of the three tank system is represented as

G ( s ) =

( s + 1)( s + 2)( s + 3)

• III.    Intelligent Controllers based on ANNs

• A.    Introduction

Neural networks find wide range of applications in nonlinear control systems modeling and implementation. The multilayer perceptron is popularly used in controlling time varying systems. Three popular neural network architectures are [2]

• •    Model Predictive Control

• •    Model Reference Control

• •   NARMA-L2 Control

System identification and controller design are the basic steps in control applications using ANNs. First stage is developing ANN model of plant i.e., three tank system in the system identification stage and the second stage is controller training. The first stage is same for all the three cases but they differ in the second stage. The following section describes the design procedure of these three intelligent controllers based on artificial neural networks. Further, the designed controllers for level control of three tank system are simulated in MATLAB/Simulink [3].

• B.    Design Procedure of NN based MPC

This is an advanced control technique to control multiple-input, multiple-output systems. The future outputs can be predicted based upon the past and current measurements. Conventional controllers can modify the control law after a variation occurs in the set point of the system but this controller can adjust the control law before a variation occurs in the set point [4].

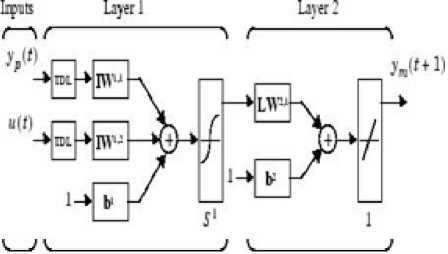
Fig.3. Neural network plant model

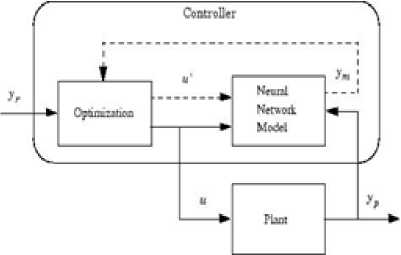
Fig.4. Block diagram of model predictive control process

This control technique is developed from receding horizon technique. The model predetermines the process output within the given time horizon. A control algorithm uses this predetermined data to estimate the optimum control signal over the defined horizon [6].

N 2                                   N u

J = X ⁽ y r ⁽ t ⁺ j ) - y m ⁽ t ⁺ j ^{))2 + P} X ⁽ u ⁽ t ⁺ j - 1) - ⁽ u ⁽ t ⁺ j — ²⁾⁾² j = N I                                         j = 1

where N1, N2, and Nu specify the error control signals evaluated time, u′ is the control signal, yr is the desired output and ym is the NN output. The ρ value determines the contribution based on least squares algorithm. The block diagram of NN based MPC is shown in Fig. 4. In the controller, the optimization block estimates the optimum control signal to minimize cost function J and this signal is given as input to the plant [7] [8].

• C.    Design Procedure of NN based MRC (MRAC)

Model Reference Adaptive Control (MRAC or MRAS) technique creates a closed loop controller in which the parameters are modified to correct the system output. The controller parameters are modified to minimize the deviation [9]. The reference model output is compared with the actual system output to meet the desired response. The architecture of NN based MRC uses two neural networks as shown in Fig. 5 and Fig. 6. First stage is plant identification and second stage is controller training to match the outputs of plant and NN model.[10] [11] .

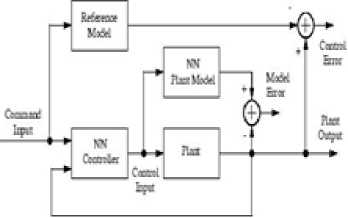
Fig.5. Control architecture of MRC

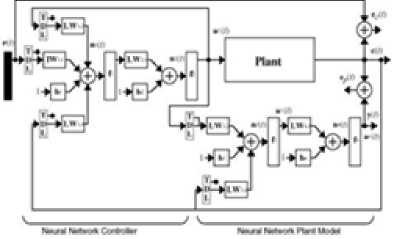
Fig.6. NN plant model and controller

• D.    Design Procedure of NN based NARMA-L2 Control

NARMA-L2 neuro controller is a discrete-time feedback controller with past control effort and output. This technique not only eliminates the nonlinearity but also the dynamic behavior of a nonlinear system [12]. Depending on the plant model, it behaves as either feedback linearization system or NARMA-L2 controller. This control strategy converts the dynamics of nonlinear process into linear process. The first step in this controller design is same as the other controllers. NARMA-L2 model is represented as [13]:

y ( k + d ) = N [ y ( k ), y ( k - 1),..., y ( k - n + 1), u ( k ), u ( k - 1),..., u ( k - n + 1) ]

where u(k) is the plant input, and y(k) is the plant response. In the first stage, ANN is trained to approximate the nonlinear function N. This is same as the identification procedure used for the NN predictive controller.[14] A nonlinear controller developed based on the reference trajectory y(k+d)=yr(k+d) is of the form:

u ( k ) = G [ y ( k ), y ( k - 1),..., y ( k - n + 1), yr ( k + d ), u ( k ), u ( k - 1),..., u ( k - m + 1) ]

The difficulty with this controller lies in creating the function G to optimize MSE, using dynamic back propagation in training a neural network. This method is relatively a slow process. NARMA-L2 approximation model based controller is shown below:

u ( k + d ) = f [ y ( k ), y ( k - 1),..., y ( k - n + 1), u ( k ), u ( k - 1),..., u ( k - m + 1) ] + g [ y ( k ), y ( k - 1),..., y ( k - n + 1), u ( k ), u ( k - 1),..., u ( k - m + 1) ] u ( k )

This model is in companion form and its advantage lies in determining the optimum control input.[15] The representation of the resulting controller is shown below.

„ л  yr ( k + d ) - f [ y ( k ), y ( k - 1),..., y ( k - n + 1), u ( k - 1),..., u ( k - n + 1) ]

y (k + d) = g [ y (k), y (k -1),..., y (k - n +1), u (k -1),..., u (k - n +1)]

The above equation can cause realization problems and so replaced by the following model:

y ( k + d ) = f [ y ( k ), y ( k - 1),..., y ( k - n + 1), u ( k ), u ( k - 1),..., u ( k - n + 1) ] + g [ y ( k ),■■■, y ( k - n + 1), u ( k ),..., u ( k - n + 1) ] u ( k + 1)

where d ≥2. Fig.7 represents the structure of NN plant model. NARMA-L2 controller architecture is shown in

Fig. 7 and block diagram is shown in Fig. 8.

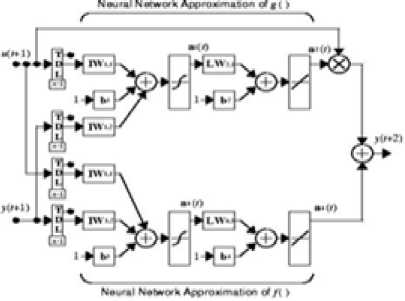
Fig.7. Architecture of NARMA-L2 controller

The next section describes the implementation of various ANN based intelligent controllers using MATLAB/Simulink.

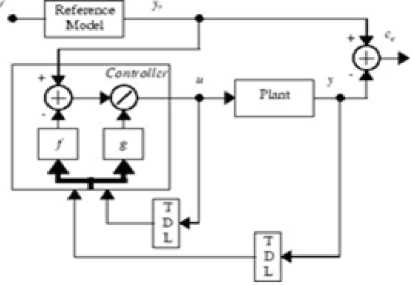
Fig.8. Block diagram of NARMA-L2 controller

• IV.    Simulation Results and Comparison

• A.    Implementation of ANN based MPC

The ANN based MPC for three tank level process is simulated using Simulink and is shown in Fig. 9.

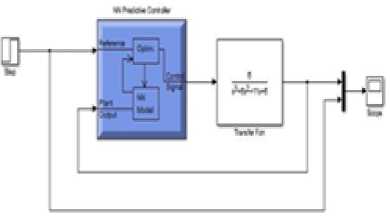
Fig.9. NN predictive controller

In the simulink diagram, the NN predictive controller is designed by setting the values of controller horizons N 2 and Nu and other parameters as shown in the Fig.10 below.

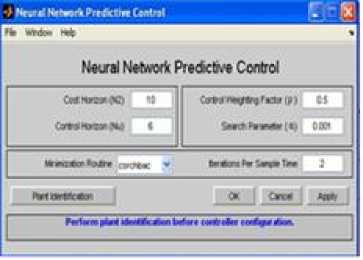
Fig.10. NN Predictive controller block

First step is plant identification shown in Fig.11. The NN plant model is developed before controller design. The NN plant model predicts future plant outputs. Various parameters like number of hidden layers, training samples, epochs and the training algorithm etc. are selected in this window.

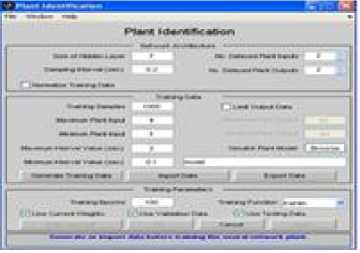
Fig.11. Plant identification of predictive control

By training the network, plant input and output is generated and is shown in Fig.12. Here, trainlm is the algorithm used for training the NN.

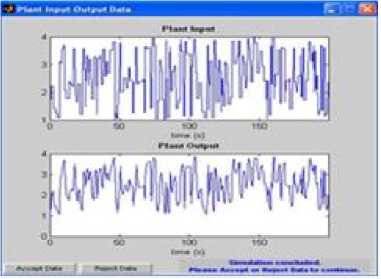
Fig.12. Plant input and output

The generated data is accepted and the closed loop system is simulated. Fig.13 shows the neural network training of model predictive controller. The simulated results for step input are shown in Fig.14.

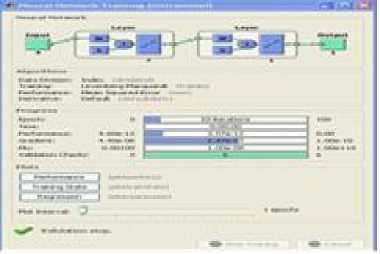
Fig.13. Neural Network Training of Predictive Control

Time domain specifications are observed from the response graph and tabulated in Table 1. From the simulation results, we observed that NN predictive controller gives smooth and fast response with no peak overshoot.

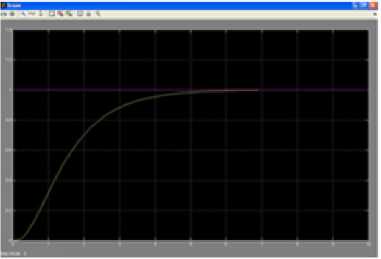
Fig.14. Response of the system using ANN based model predictive controller

• B.    Implementation of ANN based MRC

ANN based MRAC for the three tank level process is simulated using Simulink and is shown in Fig.15. Fig.16 shows the parameter selection window of the model reference controller.

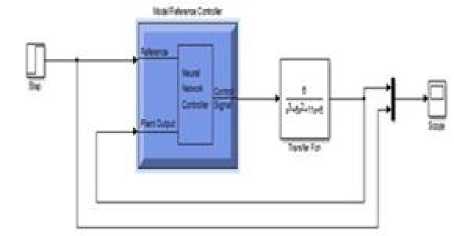
Fig.15. NN model reference controller

Once the training data is generated for the plant, then the network is trained for required iterations. Here the controller is trained using dynamic back propagation. Fig. 19 shows training window of the neural network.

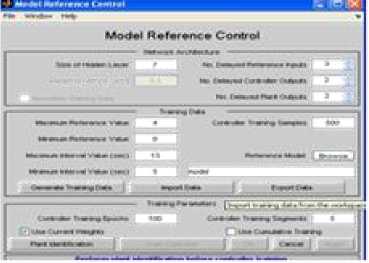
Fig.16. NN model reference controller

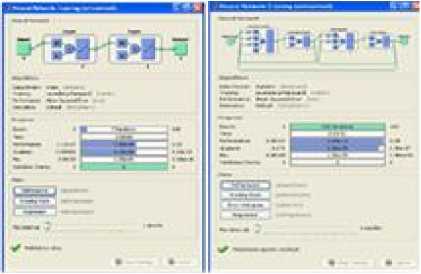
Fig.19. Neural network training

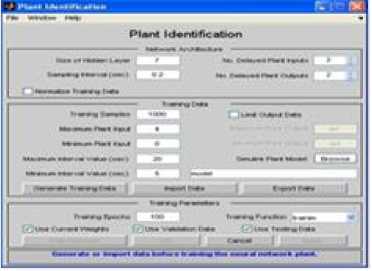
Fig.17. Plant Identification of MRC

Plant identification of MRAC is shown in Fig.17. After selecting the required parameters, the data is generated for training the controller. Then, the following window appears as shown in the Fig. 18.

Fig.18. Plant input and output

Fig.20. Response of the system using ANN based model reference controller

• C.    Implementation of ANN based NARMA-L2 Control

The ANN based NARMA-L2 controller for the three tank level process is simulated using SIMULINK and is shown in Fig.21. Plant identification of this controller is shown in Fig.22.

Fig.21. NN Based NARMA-L2 Controller

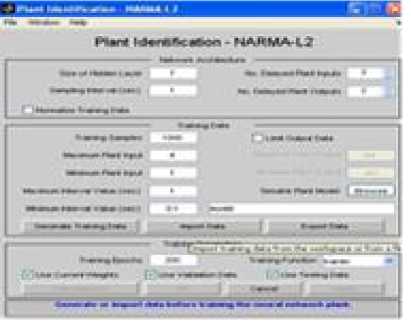
Fig.22. Plant identification

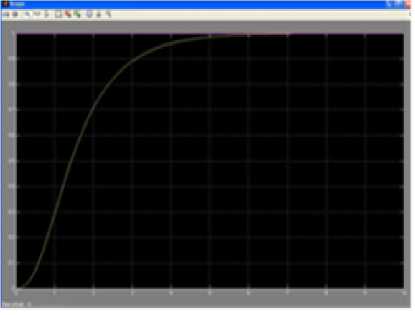
Fig.25. Response of the system using ANN based NARMA-L2 controller

The training process is not required as the plant identification is already completed. Instead, the NARMA-L2 controller is to be simulated. Then the training data is generated for training the controller. Fig.23 shows the generated training data.

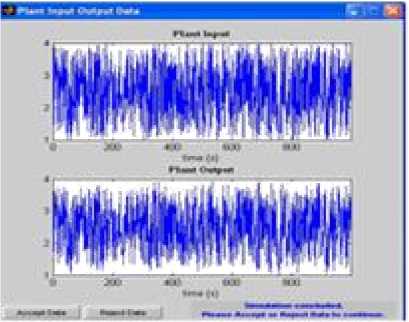
Fig.23. Plant input and output

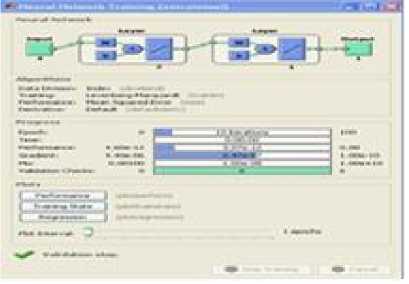
Fig.24. Neural network training

• D.    Comparison of responses of PID and ANN based Controllers

The unit step responses of different controllers for three tank level control process are compared in terms of time domain specifications and shown in Fig.26. Analysis shows that proposed intelligent controllers give better performance indices than traditional controllers.

The performance indices of the conventional PID controller and ANN based intelligent controllers are compared and tabulated in Table 1.

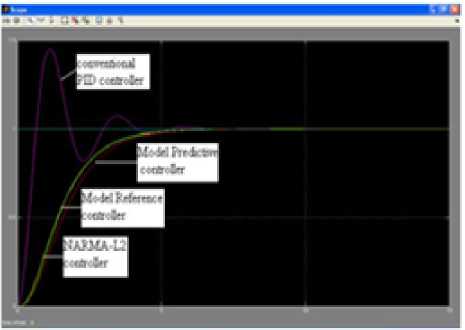
Fig.26. Comparison of responses of the system using conventional PID and ANN based controllers

Table 1 Comparison of performance indices

Time Domain Specifications	PID	MPC	MRAC	NARMA-L2
Rise time (sec)	0.6	2.65	2.78	2.52
Settling time (sec)	10	6.9	7.5	7.1
Peak overshoot (%)	45	-	-	-
Peak time (sec)	1.13	-	-	-
Steady State error	0	0	0	0

• V.    Conclusion

The response of three tank level process is proved to be fast and stable with the proposed intelligent controllers using artificial neural networks than the traditional controllers based on time domain specifications. The three intelligent controllers show smooth response without any over shoot. Out of these three intelligent controllers, NN model reference controller gives relatively sluggish response, NARMA-l2 controller gives less rise time and NN predictive controller shows minimum settling time in the response of the three tank level process. Finally we conclude that, NN predictive controller is best suited for stable control of three tank level process.