Comparative analysis of typical regulation algorithms and nonparametric dual control algorithm
Автор: Raskina A.V.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 4 т.18, 2017 года.
Бесплатный доступ
The task of nonparametric dual control algorithm and standard regulation laws (P-, PI-, PID-regulators) at dy- namic objects with discrete-continuous nature of the technological process control is considered. It means that in itself, the dynamic process is continuous, however, the “input-output” variables of the process are controlled through discrete instants. In the case under study, the structure of the process model is partially parametrized. It means that equation order is determined from prior information, but at the same time functional dependency between “input-output” vari- ables of the process remains unknown. The methods of dynamic processes modeling and control based on nonparamet- ric algorithms are offered. The complexity of dynamic process modeling and control under condition of incomplete information is discussed. This level of prior information is characterised by the lack of model structure knowledge, but the information on object qualitative characteristics, for example, unambiguity, or ambiguity characteristics, linearity for dynamic processes or the nature of its nonlinearity is required. Methods of nonparametric statistics are applied to identification problem solving at this level of prior information. The problems of identification and control in the conditions of incomplete information are very relevant because many dynamic processes are not deeply studied and the presence of unknown distribution random noises causes more complexity in solving the identification and control tasks. The results of computing experiment which show the efficiency of nonparametric dual control algorithm in comparison with standard regulators are presented
Dynamic process, nonparametric dual control, adaptive systems, standart regulators
Короткий адрес: https://sciup.org/148177764
IDR: 148177764 | УДК: 62.501
Текст научной статьи Comparative analysis of typical regulation algorithms and nonparametric dual control algorithm
Introduction. At present, widespread types of various control processes regulators are control devices based on the use of standard control laws (P, PI, PID regulators and their versions). It should be noted that when using these systems, the quality of control is not sufficiently effective. It should be noted that in some cases the quality of control when using similar systems is insufficiently effective. This is basically due to two main factors. First, the typical regulators use the information about the deviation of the output quantity from the control action when generating control actions. In this case, the data on uncontrolled input influences, which also affect the process output, are often not taken into account. Secondly, the standard regulators are not training and adaptive. This means that when the object is transferred from one control action to another, the regulator will not improve performance. This significantly increases the time of overshooting, and consequently, increases the possibility of going beyond the limits of the technological regulations. In this regard, the issue of developing new control systems to solve these problems is topical. One of the possible ways of solving the control problem is the use of dual control algorithms [1–4]. This article is devoted to the question of comparing the efficiency of using two methods in the control of a dynamic system.
The control device designing. The control system consist of two main elements: a controlled object and a regulator (control unit) – a device that performs the functions object control. The simplest functional control structure is shown in fig. 1 [5].
In fig. 1, the following notations are accepted: u ( t ) is the input control action, x ( t ) is the output control action, x *( t ) is the setting action (the desired output).
Let us introduce the object A operator, which describes the process, that is: x ( t ) = А < u ( t ) > . If there exists an operator inverse to A , that is A - 1 , when A - 1 A = 1 is the unit operator, then:
А - 1 x ( t ) = А - 1 A < u ( t ) > , (1) u ( t ) = A - 1 x ( t ).
Setting the trajectory x ( t ) = x* ( t ), the ideal value u* ( t ) is found from (1). Thus (1) can be referred to the category of ideal regulators. However, the problem is that the operator A is unknown. Also, when constructing a control system, it is necessary to take into account that equality of the setting and the output actions is almost impossible to achieve. This is due to the presence of various noise in the system, inaccuracy of the inverse operator restitution and others. Therefore, it is necessary to introduce the feedback, which modifies control actions during the process (fig. 2).
Depending on the system characteristics and the amount of a priori and current information, one or another control scheme is selected. Today, there are many methods used to solve the control problem. Further, we will consider two approaches to be compared in this article.
Typical control algorithms. One of the most widespread regulators in practice are standard P-, PI- and PID-regulators. Typical regulators are classical in the theory of automatic control. The controller parameters can be set either manually or automatically. The setup process has two main steps: the identification of the controlled object model and the setting of the optimum parameters of the regulator. Before choosing the initial approximation of parameters, it is necessary to determine the purpose of control and the used criteria of quality [5].
Among the tasks for which solution regulators of various types including P-, PI-, PID-regulators are used, the tasks of a defined value parameter maintaining, a problem of program control and others are met. Let the task of tracking be set, that is, the desired trajectory x *( t ) is provided to the input of the object. All standard regulators assume feedback. The P-regulator generates control effect proportional to the error value: e = x - x * with a proportionality coefficient K 1 . The I-regulator generates control effect proportional to the integral of the error with a proportionality coefficient. PI-regulator is a combination of P and I regulators, the result of their serial connection. D-regulator generates control actions proportional to the derivative, the controlled variable with the proportionality coefficient. The PID regulator is a combination of all three regulators.

Fig. 1. Control system without feedback
Рис. 1. Разомкнутая прямая схема управления
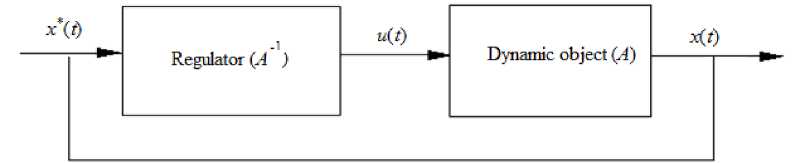
Fig. 2. Control scheme with feedback
Рис. 2. Схема управления с обратной связью
It is clear that the quality of regulation depends on the appropriate regulators setting, and in some cases is not effective enough. To make a control scheme, it is necessary to choose the coefficients that would ensure stability and the best quality of control. The manual setting of the regulator is performed after initial approximations of parameters were calculated by any method, using the identified model. It can be manually done, based on the rules derived from experience, theoretical analysis and numerical experiments.
Dual control. The deficiency of a priori information results in the necessity to combine learning and controlling the object. This type of control is called the dual control. The dual control was discovered by A. A. Feldbaum in 1960 and its further development was based on the statistical decision theory [6]. It is worth noting that the training control systems are the systems that have a “memory”. In other words, they are able not only to examine the object performance data, but also to develop reasonable control actions. The theory of dual control gained further development in researches of various authors, in particular B. Wittenmark [7]. In the last research the attention to bulkiness of analytical results on synthesis of an optimum control algorithm is paid and substitution of control algorithms in the form of nonoptimum dual regulators is carried out. Under conditions of smaller prior information the problem of dual control was considered by Ja. Z. Cypkin [8; 9]. Here the prior requirements to probability random factors density weaken, but the knowledge of a research object parametrical structure is required.
Nonparametric dual control algorithm, described in detail in [10] in a discrete form:
u s + 1 = u * + A u s + 1 , (2)
where us * – an augend accumulating the knowledge about the object, for subsequent formation of adaptive control action; A u s + 1 = e ( x * + 1 - xs ) - “learning” search steps.
The parameter £ is found from the minimum of the quadratic criterion £ :
s
R ( £ ) = 2 ( x * + 1 k = 1
x
= min, k ^ i . £
This is the dualism of the algorithm (2). The first augend us * of equation (2) depends on the level of a priori information about the object of study.
The state of a one-dimensional dynamical system at a given time depends on the input actions and on its states in the past [11]:
x t = F ( x t - 1 ,”•> x t - k , u t ) , (4)
where k is the known depth of memory (in the terminology of A. A. Feldbaum) [6], found somehow from the available a priori information. If we draw an analogy with the description of the studied process in continuous time in the form of differential equations, then k is the order of the highest derivative in the differential equation. Here is essential that the type of a functional is not defined to within parameters. It is a situation where the control problem is formulated under the conditions of both parametric and nonparametric indeterminacy [11]. It should be noted that the discrete equation (4) has a corresponding analogue among the differential equations.
Let us introduce the following re-designation [12]:
z t = ( z ! , ^ , z k + 1 ) = ( x t - 1 , - > x t - k , u t ) ,
where
xt = f ( zt ) . (6)
Thus, the structure of the process model (4) can be partially parametrized. In this case, the task of a dynamic system control is reduced to the task of a static system control by introducing a mathematical re-designation (5)–(6). Taking into account the re-designation data (5)– (6), the control scheme can be shown in the following scheme (fig. 3). The diagram illustrates a model of a dynamical system in discrete time, reduced to a model of a static system, when variables u t and xt - 1 , ..., xt - k are input variables of the process [13; 14].
As a nonparametric model of the process, the following nonparametric estimation of the regression function can be adopted:
xt
s
2 и-ф i=1
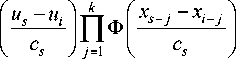
s
2ф i =1
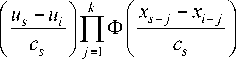
Formula (7) is a direct operator A , then the inverse operator is (8):
s
2 и-ф i=1
*
x s + 1
k
ПФ j=1
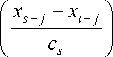
s
2ф i=1
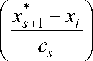
k
Пф j=1
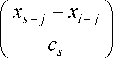
where Ф( - ) nuclear bell-shaped function [15]. The formula (8) is the augend us * from equation (2).
Let us consider the dualism of the algorithm (2). In the initial stage of control, the main role belongs to the second addened A u s + 1 from formula (2). It is a case of active information accumulation in the system of dual control which begins with the first observation of input and output variables of an object emergence. As learning proceeds (with the accumulation of information), the augend us * plays an increasing role in forming the control action u s + 1. Thus, in the course of object dual control both the stage of studying of an object, and a stage of its reduction to the purpose appear.
Let us compare the results of nonparametric dual control algorithm (2) and the standard algorithm PI-regulator. The sample size ( ui , xi ) is 100. We present the work of two control algorithms at the changing control action (fig. 4).
In fig. 4 the following notations are accepted: x ( t ) is the object output when the control unit is a nonparametric dual control regulator, x ( t ) is the object output when the control unit is the PI regulator, x * ( t ) is a control action
(set points). The control error for the nonparametric regulator is 0.07, for the PI regulator is 0.34. In the experiment presented in fig. 4, the augend of the dual control algorithm (2) is equal to equation (8). Let us consider the work of nonparametric dual control algorithm in detail. Control training begins with the first dyad observations x1,u1. On the initial control stage some time (accumulation of sample) is required to bring the object to a set state, but on the next steps, the algorithm almost instantly reaches the task.
Let us imagine the situation when х* ( t ) is set in a random way (fig. 5).
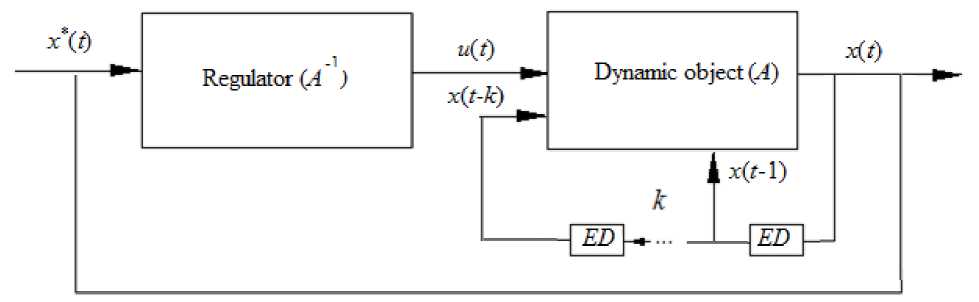
Fig. 3. Dynamic process control diagram, where ED is the delay element
Рис. 3. Схема управления динамическим процессом, где ED – элемент запаздывания
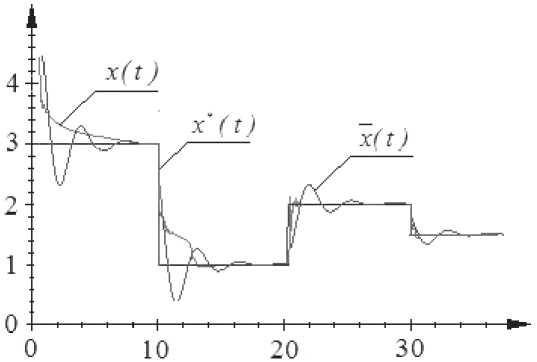
Fig. 4. The control results at a stepwise action
Рис. 4. Результаты управления при ступенчатом задании
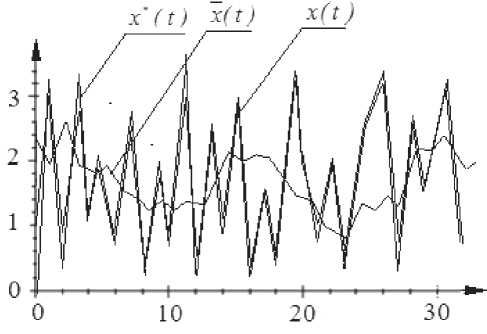
Fig. 5. Control results at random task
Рис. 5. Результаты управления при случайном задании
Fig. 5 shows the operation of two control algorithms in case of random setting. In this case we illustrated the situation when the nonparametric dual control algorithm obviously surpasses the standard PI-regulator. From the given figure the high quality of control by means of the nonparametric regulator is visible, even at such “exotic” option when the task is random. Not any known regulator will cope with a similar task. These results are of considerable interest only from the theoretical point of view because in practice this option is not found.
Conclusion. In the article the algorithms for nonparametric control and standard algorithms (P-, PI-, PID-regulators) under condition of nonparametric indeterminacy are analyzed. In the present article, the functional dependence between input-output variables of the process is unknown, and it is impossible to uniquely determinate parametrical structure of object the model, a differential equation, or its transfer function. Therefore, the standard control algorithms which form the control action due to the feedback within the observation error (residual), in particular PI-algorithm which does not require the knowledge of the object model parametric structure, are chosen as the object of comparison In this case, the discrete equation is used for describing the process. The problem is reduced to the solution of nonparametric estimation of regression function using observations of the object “input-output”. The use of nonparametric algorithms under partial nonparametric indeterminacy is illustrated in the computational experiment. The simulation results showed a significant superiority of nonparametric dual control algorithms over standard regulators at different control action values.
Список литературы Comparative analysis of typical regulation algorithms and nonparametric dual control algorithm
- Wenk C. J. Bar-Shalom Y. A multiple model adaptive dual control algorithm for stochastic systems with unknown parameters//Automatic Control, IEEE Transactions. 2003. Vol. 25, iss. 4. Pp. 703-710.
- Duan Lia, Fucai Qianb, Peilin Fuc. Optimal nominal dual control for discrete-time linear-quadratic Gaussian problems with unknown parameters//Automatica. 2008. Vol. 44, iss. 1. Pp. 119-127.
- Tse E., Bar-Shalom Y. An actively adaptive control for linear systems with random parameters via the dual control approach//Automatic Control, IEEE Transactions. 2003. Vol. 18, iss. 2. Pp. 109-117.
- Filatov N. M., Keuchel U., Unbehauen H. Dual control for an unstable mechanical plant//Control Systems, IEEE. 1996. Vol. 16, iss. 4. Pp. 31-37.
- Куликовский Р. Оптимальные и адаптивные процессы в системах автоматического регулирования. M.: Наука, 1967. 380 c.
- Фельдбаум А. А. Основы теории оптимальных автоматических систем. М.: Физматгиз, 1963. 552 с.
- Wittenmark B. Adaptive dual control methods: An overview//In 5th IFAC Symposium on Adaptive Systems in Control and Signal Processing. Budapest, 1995. Pp. 67-72.
- Цыпкин Я. З. Адаптация и обучение в автоматических системах. M.: Наука, 1968. 400 с.
- Цыпкин Я. З. Информационная теория идентификации. М.: Наука: Физматлит, 1995. 336 с.
- Медведев А. В. Основы теории адаптивных систем/СибГАУ. Красноярск, 2015. 525 с.
- Медведев А. В. Теория непараметрических систем. Моделирование//Вестник СибГАУ. 2010. № 4 (30). С. 4-9.
- Медведев А. В. Адаптация и обучение в условиях непараметрической неопределенности//Фундаментальные исследования (физико-математические и технические науки). Новосибирск: Наука. Сиб. отд-ние, 1977. C. 92-97.
- Раскина A. В. Определение структуры линейного динамического объекта в задачах непараметрической идентификации//Вестник СибГАУ. 2016. № 4. C. 889-891.
- Банникова А. В., Медведев А. В. Об управлении объектами с памятью в условиях непараметрической неопределенности//Вестник СибГАУ. 2014. № 5(57). С. 26-37.
- Надарая Э. А. Непараметрические оценки плотности вероятности и кривой регрессии. Тбилиси: Изд. Тбил. ун-та, 1983. 194 с.


