Comparative Analysis of Various Inter-Carrier Interference Cancellation Methods

In OFDM, there are distinct carriers that carry different frequencies with various modulations. As the signals are orthogonal to each other, there are various overlapping frequencies that are simultaneously transmitted along the channel. Due to severe channel conditions, carrier frequency offset or Doppler’s shift, the orthogonality gets disturbed leading to interference among various carriers [1]. This phenomenon is known as Inter Carrier Interference.

To counter the issue of Inter Carrier Interference, various schemes have been devised. These Inter-Carrier Interference (ICI) cancellation schemes have their own advantages and disadvantages. Some of the schemes are Self-cancellation, channel equalization, channel estimation and time domain windowing. This paper is provides a comparative analysis of the above said Inter Carrier Interference cancellation techniques. The Carrier to Interference ratio of the signal due to various schemes has been discussed under the similar channel conditions because the comparative reliability of one method against the other gets easily demonstrated when channel conditions are same.

* Corresponding author. Tel.:

OFDM multiplexes the incoming single signal into N different signals that are all modulated by N different carriers by Inverse-Fast Fourier Transform (IFFT). The cyclic prefixing (CP) is followed by the signal sent on discrete time channel. At the receiver, the CP is removed, signal is de-mapped and decoded according to the desired technique [2].

The time-domain representation of the transmitted signal is given by [2]:

х (и) = l/TVE^V^COe^2 "l//N

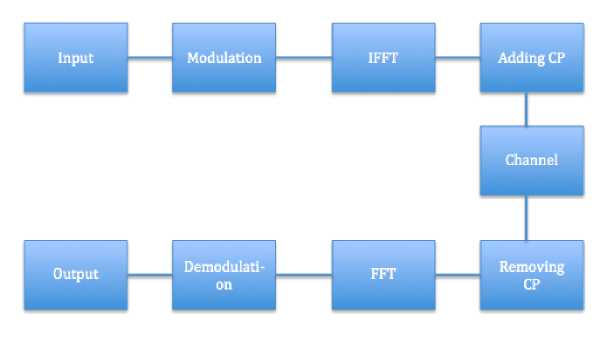
Fig. 1 Simplified OFDM transmission and reception [5]

Nomenclature

a(k) Cd (M f?) fdi Нй m N Pfranк (O P^; quist (0 PsoCW (Й S(l-k) Tu uo w(k) x(n) X(l) Y(k) a a 0 St

Modulated data sequence prepared from the frequency domain Correlation between two ICI gain vector Frequency domain representation of «(•) Doppler’s frequency ICI gain vector Subcarrier Number of subcarriers Frank window pulse Nyquist window pulse using a raised cosine function SOCW window pulse ICI coefficient Length of useful interval of an OFDM symbol Frequency domain representation of AWGN Additive White Gaussian Noise (AWGN) tv 1 h sample of the transmitted signal Modulated symbol within the I1 h subcarrier Frequency domain response Roll-off factor Complex fading envelope in equivalent complex baseband channel Normalized frequency offset for i 1 h path

^f

Frequency difference between the carrier

The received signal is given by:

у (п) = [x(n) + w(n)]ey 2 ""/^

After FFT, the frequency domain response is given by:

У (к) = Х(к)5(0) + Z^XCOSC I -к) + п (к),     к = 0,1.....N - 1

I Фк

ICI coefficient is given by:

S(I -к) = sin(7r(I - к + £)) /Nst^^^^eU^1 -^)(i-к+£))

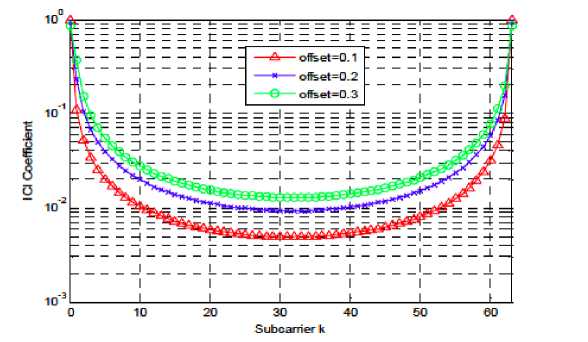
Fig. 2 Amplitude of S(l-k) [5]

As shown in fig. 2, amplitude of ICI increases as the frequency offset value (normalized here) gets hiked. Therefore, for the purpose of decreasing the ICI power, the given ICI cancellation techniques have been reviewed in this paper.

The paper is organized as follows: Section 2 contains review on the Self-cancellation technique, section 3 comprises of the Equalization technique, section 4 has a review on the Estimation techniques and section 5 includes the Windowing technique’s review. Finally, the conclusion of the paper is presented in section 6.

• 2.    Self-cancellation Technique

• 2.1.    Modulation[4]

The main aim of this scheme is mapping of input data symbol onto a group of subcarriers that have predefined coefficients. The generated ICI signals cancel each other, which led to its name self- cancellation. Looking at it otherwise, when the number of sub-carriers is N, the data block length is considered as N/2. There are adjacent pairs of carriers for one data symbol with one multiplied +1 and the other by -1 [3]. This scheme reduces the ICI considerably but has a big drawback of more bandwidth consumption where we have only 50% of the available bandwidth to transmit the signal.

Mainly the modulation requires that the signal X(N-1) = -X(N-2). So, X (1) = -X (0), X (3) = -X (2), X (5) =

• - X (4), X (7) = -X (6) and so on. If there are two subcarriers, m and m+1, the received signal can be written as

• Y ' (m) = XNfc=o X(/c)[S(—-m)-S(к + 1 - m) + nm(5)

k=even

• Y * (m + 1) = ^^ к=o -^ (—)[S (к — m — 1) — S(к — m) + nm + ^

• 2.2.    Demodulation[4]

k=even

The ICI coefficient S’ (n-m) is given by

S' (n — m) = S(n — m) — S(n + 1 — —)

Demodulation is expressed mathematically as:

Y "(m) = 7'(m) — 7'(m + 1)

Where (m + 1) ^£h subcarrier is subtracted from m ^£h subcarrier.

• У' ' (ш) = ^^ ^=0 X (—) [—S (к — m — 1) + 2S (к — m) — S(к — m + 1) + nm — n^+^

k=even

The ICI coefficient of the same is given by

S’(k-m) = -S (k-m-1) +2S(k-m) – S (k-m+1)

Theoretically, the CIR is given by

|-5(-1) + 25(0)-5(1)|2

Sfc-2 4 6 I"^(k-U+25(k)-5(k+DI² , , ,■■

We generally obtain a higher CIR in case of Self-cancellation technique compared to the simple OFDM reception.

Selfcancellation

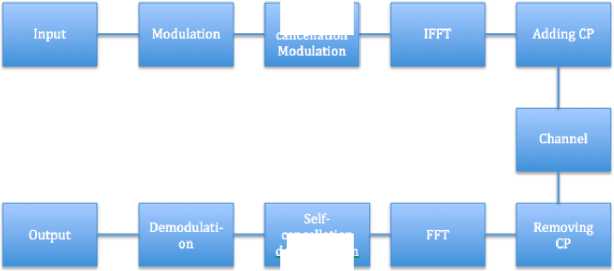
cancellation demodulation

Fig. 3 Simplified Self-cancellation technique in OFDM

The parameters studied in this scheme are i) Carrier to interference ratio (CIR) ii) the Bit error rate (BER). Generally, in this scheme, the carrier frequency offset, which is denoted by £, is kept constant. The CIR and BER are studied against various parameters, for example the carrier frequency index given by k or frequency offset в .

Zhao studied the carrier frequency error and sensitivity to Doppler’s shift in OFDM systems during 1996 [3]. The concept of subcarrier frequency offset response (SFO) function has been introduced, which relates the ICI property to the frequency offset [3]. The studies are done in time-variant multipath radio channel.

The normalized frequency offset for I^th path is given by

Ei =   /Δf

The results are performed for MPSK modulation and the CIR for general OFDM system is given by:

=

2£2

The proposed scheme improves the CIR by 10dB. The scheme also allowes the £ to increase to even 22% that helped in keeping the CIR to more than 20 dB.

The scheme allowes the BER to decrease to a value little less than 10 2 as against the BER of considerably lesser than 10 2 in case of [5]. In [5], two simple steps are employed. At the transmitter adjacent subcarriers are used with a group of weighing coefficients to modulate one data symbol onto them and at the receiver, these carriers are linearly combined to further reduce the ICI.

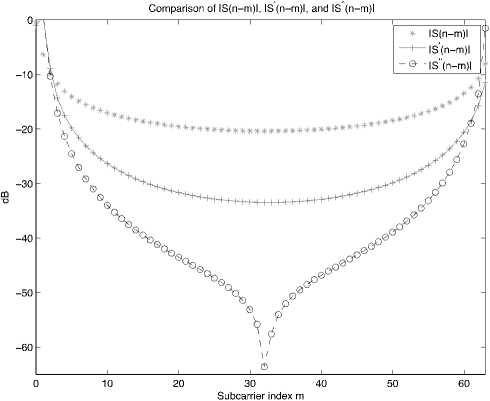
Fig 4. Comparison of ICI before modulation, after modulation and after demodulation at 5=0.4 mid N =64 .

Unlike the Zhao scheme, it claims to increase the CIR by 15 dB to 20 dB as compared to 10 dB increase. From the inference curves, for a given N = 512, BPSK, QPSK and 16 QAM give almost the same result, where S is changed between 0 and 0.5. CIRs of approximately 40 dB and 0 dB are obtained at £ = o and 0.5 respectively. Similarly, for a given £ maximum change of 0.068 dB is obtained when N ≥ 8.

During modulation, the ICI carrier is given by eqn. 6 where at N = 64 and £ = 0.3, S’ (k-m) = 10 3 and S (k-

• m)    = 10 ¹ and the difference decreases as the index increases towards 0 and 60 dB. Also, comparatively, if coherent addition is done then the CIR improves by 17 dB compared to conventional schemes where signal level grows by a factor of 2.

There has been a constant difference between the ICI self-cancellation simulation and the standard OFDM systems with a £ = 0, CIR is more than 50 dB in case of self-cancellation and almost 35 dB for normal OFDM whereas at £ = 0.45 the CIR values are 20 dB and 0 dB.

Signal mappers are used in [6] where (a,-a) is mapped onto (a, ^ 16 ). Optimal values of ц and 9 are showed to get a CIR improvement of 10 dB compared to previous OFDM system. The curve’s maxima i.e. the maximum value of CIR occurs at 6 = . Conventional ICI has ц =1 and as г hikes, CIR increases for lower values of ц . Compared to previous schemes at г = 0.5, CIR attainable is approximately 30 dB compared to the conventional OFDM self-cancellation.

Paper [7] analyses BER performance in terms of phase noise variance under the SNR value of 10dB. The author has used data-conversion method and data-conjugate method. He showes a significant improvement in BER than original OFDM. A phase noise of less than 0.02 doesn’t affect the performance or BER of 16QAM. At phase noise of around 0.1, only 16-QAM shows a BER of around, rest all h10 3as BER above this. Hence, 16-QAM has the best performance in the environment.

Author in [8] shows that CIR performance of proposed system closely matches the conventional OFDM. In this the transmitted symbols are data coded as follows: X (1) = X (0) е i” ^/2 and so on.

Table 1. BER comparison of Zhao’s [3] and Proposed BER [8] at an SNR of 5 dB

Frequency Offset	Zhao’s BER	Proposed BER [8]
0	Much less than 10	Slightly less than Zhao’s
0.15	10	10  .5
0.25	Slightly less than 10	Approximately 10  .5

Hence, BER of Zhao’s scheme is higher than that of proposed scheme. It is easy to implement and the complexity is low because no coding is required for phase error reduction.

Comparison between conventional, Sheu, Chang and proposed schemes [10], [11], [12], [13] has been made in terms of BER and ICI+noise at various signal to noise ration (SNR) values. Author proposes an optimal weight combining calculation method to reduce the ICI and noise in the signal. Below 15 dB, the difference between conventional, Sheu, Chang and proposed schemes is not visible but after this SNR value proposed and Sheu schemes perform equally well as well as better than the other schemes. Similarly, BER of Sheu and Proposed schemes, at a redundancy of 64, give the best results. At longer redundancy of 256, Chang and author’s proposed scheme perform the best but the proposed scheme outperforms the Chang’s method at various SNR values. At 128-redundancy length, Chang and Sheu perform equally well and the author’s method performs far better than both the schemes.

At an offset of 0.1, [14] performs better than [3]. The performance is similar at an offset of 0.2 but after this value the CIR degrades compared to previous schemes. So, this scheme is better than the rest if the values of offset are small.

• 3.    Equalization Technique

The sampled time-domain signal after travelling through a non-selective fading channel, received at the receiver is given by [15]:

г (и) = 1 а(п) Хк=о a(k)ei(2 nnk/lN + w(n) (14)

The demodulated symbol of the same is given by:

у(т) = T,k“oa(k)f (m - к) + и(т) (15)

• J. Ahn has used the concept of frequency domain equalization in [15] to decrease the effect of deep fades on the transmitted signal. The author uses equalization after the demodulation of the signal and claims to have a better SER compared to the previous techniques. The comparison of the results has been made with the Cimini technique where fading distortion was compensated through phase and gain correction of the signal at the receiver. The concept is to estimate the ISI at first place. This has been done by inserting frequency domain pilot symbols in each of the frames having variable level of ISI. This is followed by usage of Zero-Forcing criteria [16] for knowing the equalizer coefficients that are helpful in eliminating ISI.

The comparison is made between the schemes proposed by Cimini (TDUGC – Time Domain Unlimited Gain Correction and TDLGC – Time Domain Limited Gain Correction) and two new schemes proposed in the paper (FDLE – Frequency Domain Linear Equalizer and FDDFE – Frequency Domain Feedback Equalizer). Results show that TDUGC provides an SER of no less than 10 “⁴ at Doppler’s spread values of 20 Hz and 100 Hz thus causing an issue of noise enhancement. FDDFE shows the best performance compared to other three and the performance of FDLE is between that of TDUGC and TDLGC. This is due to finite length of equalizer used in the scheme that causes residual ISI after equalization.

Another low-complexity equalization technique is proposed in [17] where Channel Impulse Response (CIR) is utilized for the purpose of studying the efficiency of Equalization technique. The CIR is estimated by averaging consecutive CIR estimates obtained by conventional approach and the estimate is made in middle of OFDM block. This technique necessitates the estimation of channel matrix for frequency selective and timevarying multipath fading channels. In slow time-varying channel with relative Doppler frequency change of less than 0.1, the relative Doppler change signifies the degree of time variation of CIR and helps in simplifying the following matrix equation:

Y = HX + W (16)

The above equation helps in easy equalization and hence helps in decreasing the complexity. Three Doppler’s frequencies (20 Hz, 100 Hz and 200 Hz) have been used in the proposed scheme. The scheme claims to have better performance when it comes to multipath fading distortion. Though the performance is not very good at

• 20 Hz, there is a profound difference as the Doppler’s frequency increases. Where at 100 Hz, conventional scheme provides a BER of approximately 10 “ ^1.5 , the proposed scheme gives a BER of less than 10 “ ³ at an SNR of 36 dB with matrices of sizes: 1 by 1, 3 by 3, 5 by 5 and full size. At similar parameters, conventional scheme gives a BER of approximately 10 “² and proposed scheme has BER of between 10 “¹ ■⁵ and 10 “³ .

• 4.    Estimation Technique

A one-tap Decision Feedback Equalizer (DFE) is proposed in [18]. An OFDM without guard band and a scheme with 100% bandwidth and data efficiency are used. Two systems have been compared: SYSTEM 1 and SYSTEM 2. System 1 has an efficiency of 67% in terms of bandwidth and data usage and sampled data is said to be ISI and ICI free. On the other hand system 2 has data usage efficiency of 100%, the signal is oversampled and is ICI and ISI infected. System 2 makes use of DFE equalizer. At an SNR of 20 dB, system1 gives a BER of around 10 1.5 whereas system 2 gives a BER of 10 3 . The paper claims to have an SNR better than that of ISI and ICI free system by 3 dB. As the value of SNR increases, the difference between the SER values of System 1 and 2 increases constantly which shows that system 2 with proposed equalization performs better.

Compared to Minimum Mean Square Error (MMSE) and Zero-Forcing (ZF) estimation, [19] provides lesser computational complexity. [19] has a two-stage equalization process in doubly selective channels. The scheme uses signal-to-interference-plus-noise (SINR)-optimal low-complexity linear processing that squeezes ICI into fewer coefficients. It includes decoding method, which is preceded by detection using estimation. Also it proposes the usage of linear pre-processor, which helps in simplifying the estimation process by making the ICI response sparse and uses MMSE iterative symbol estimation. The averaged SINR performance of various windows is compared and hamming window is shown sub-optimal at higher SNR and Rectangular window is suboptimal in all but lower SNRs. Also, the MSE comparisons have been studied but study of these parameters is beyond the scope of our paper.

Apart from the above, a banded scheme [20] uses Block MMSE (jointly equalizes all sub-carriers) against serial MMSE (separately equalizes all sub-carriers) and makes use of band-structure of frequency-domain channel matrix that in turn uses LDLH band factorization of Hermitian band matrices. This factorization matrix helps in reducing complexity to a greater extent. Also, Tv multipath channel has been considered which provides a nearly banded channel matrix. The equalization process is summed up as follows: Choose a value Q that balances complexity and performance and construct a band matrix given by B = Λ∘т(Q), where the former is channel matrix and the latter is a matrix with lower and upper bandwidth Q and all ones within its band. After this, construct the band matrix M = ввн + X ^Мд , where NA = number of subcarriers. Perform the LDLH factorization of M and finally solve the system Md = z. This can be done by first solving the triangular system Lf = z, then the diagonal system Dg = f and finally the triangular system LHD = g and calculate aLDL =     . Compared to a total complexity of (8/3 Q3 +20Q2 +у Q + 4) Na in case of serial MMSE, the block MMSE (proposed) has a lesser complexity of (8Q2 +22Q +4)na complex operations. The results have been noted for Q = 2 where it is shown that serial MMSE has the best performance. The proposed scheme performs similarly but complexity has reduced by 43% for the given value of Q. Zero-forcing serial banded equalizer gives the worst performance and the conventional 1-tap equalizer shows a comparatively better performance than the former one where at an SNR of 20 dB, conventional equalizer has a BER of approximately 10 1.5 and the serial and block MMSE (both banded) give approximately similar performance at around 10”2 .5 with serial MMSE performing better. One-Tap Equalizer (OTE), MMSE equalizer (SIREQ) based on signal to interference ratio (SIR)[21] and computation of inverse of the equalization matrix in a recursive fashion have been used in another technique named as Improved SIREQ (ISREQ) [22]. The SER of SIREQ and OTE + ISIREQ at a tap length of 15 is the same. Below the value of 25 dB REQ and OTE + ISIREQ for a tap length of 7 have similar SER, whereas for SNR of above 25, REQ gives a better SER value. The findings claim that the scheme gives 75% of computational savings compared to convectional techniques.

Time domain estimation helps in finding and tackling the frequency offset that causes ICI and amplitude reduction at the filter output in OFDM through Maximum Likelihood Estimation (MLE) algorithm [23]. It takes advantage of the fact that the phase shift is proportional to the frequency offset and both the signal and the ICI, change through the same phase shift. So, it is very easy to obtain the estimate when the offset is known, irrespective of its value. Two values of E_c / N_o (individual OFDM carrier energy to one sided spectral density of additive white Gaussian noise [23]) have been used. The values are 5 dB and 17 dB. The original value and the estimated value give almost similar results at both the above given values with only minor differences (variance) between the given and estimated frequency offsets (at certain values). In case the offset value is not between the ±1/2 the carrier spacing, then an acquisition method has been used that shortens the DFTs (Discrete

Fourier Transforms) and enlarges the carrier spacing such that the phase shift remains between +n and — n. Along with frequency-offset estimation, symbol time (arrival time of OFDM symbol) can also be estimated through a joint Maximum Likelihood Estimation (MLE) [24]. Using the above said concept, which says that all signals experience same amount of offset, estimation can be done as a function of channel impulse response (8(к — 9),9 = arrival time of the symbol and k = carrier’s index) and time domain complex distortion of received signal (e n where e = difference between the transmitter’s and receiver’s oscillators and 1/N is the normalized frequency) and the offset is calculated in terms of difference between the given and estimated Signal to Noise Ratio (SNR). Both the frequency and time estimators are tested for given values of samples in the cyclic prefix, L (in terms of mean-square values). After L = 6, time estimators cease to show any improvement (at SNR =10 dB and 16 dB) whereas the improvement continues till the value of 12 (L) for lower value of SNR (4dB). In case of frequency estimators, improvement is large for certain lower values of L but doesn’t degrade at larger values too. The given estimators perform well in AWGN channels and the performance relatively degrades in dispersive channels.

Apart from the above mentioned estimators, a second-order time-domain Channel Impulse Response (CIR) tap variation estimator [25] is utilized which measures the variations in CIR tap values, helps in estimation at the output and has an advantage of not requiring any pilot information. Firstly, it iteratively obtains tentative symbol decisions without using ICI cancellation, then it estimates the CIR tap variations based on first iteration’s results, consequently performs frequency-domain ICI cancellation and finally gets symbol decisions from the results. BER performance of a system deploying 8-tap Weiner filter prediction assisted decision-directed Channel estimation is observed. Various cancellers are compared and MMSE canceller is found to perform best among Zero-Forcing (ZF), subtraction canceller and MMSE canceller. Also, ZF performs better than subtraction canceller for QPSK and worst for BPSK. A larger difference among their performance is observed after 20 dB SNR. In time-varying cases where discrete time structures are considered, different channels involve the measurement of different channel responses. This task of considering all channel responses can be reduced by linear interpolation [26]. Using a pilot placement technique (where pilot tones are placed in groups against the scheme of placing pilot tones equi-spaced [27]) a significant improvement in SINR is reported. Channel matrix is observed and the variation in the rows differentiates the performance of linear interpolator and jakes- interpolator’s. At a Doppler’s frequency of 858 Hz, where variations are large, jakes performs significantly better in terms of SINR. Otherwise both the interpolators can be employed as the performance in given conditions is almost the same. In place of time-domain estimators, frequency domain estimators estimate both channel Frequency Response (CFR) and frequency offset. The author has proposed a binary search algorithm that uses the correlation properties of CFR to find the best channel estimate by hypothesizing different channel offsets. The paper uses the residual frequency offset (difference between the actual frequency offset and frequency offset hypothesis) to find the correlation of CFR, which is used as a decision criterion. CFR can be calculated through interference matrices for each frequency-offset hypothesis. The interference matrix is truncated around the diagonal because most of the energy is concentrates around it [29]. The authors have compared Least Square (LS) method and the method proposed by them in terms of MSE. At a normalized frequency of 0.5, the method proposed by the author performs better as the SNR increases. The difference between the MSE of both the methods become significant after 15 dB SNR. Also, the truncation of interference matrix shows its effect only at an SNR of 30dB.

An improved spectral efficiency of 6.83% has been claimed in [30] by using cyclic prefix reconstruction (CPR) method. By using residual ICI cancellation (RISIC) on space-time block coded (STBC) OFDM system and by applying the channel estimation (CE) algorithm on the same, better results have been found [31]. The STBC OFDM with insufficient Cyclic Prefix (CP) has been considered. Compared to systems with no CPR, system with CPR and proposed estimation with cyclic prefix length of 2 perform better. [32] has adopted frequency domain correlation method in place of time-domain correlation, which makes use of off-diagonal vectors of Channel Frequency Response Matrix (CFRM). It utilizes the fact that ICI gain along the off-diagonal matrix vectors has the same correlation as that of channel gain vector. By using simple estimation method of LS estimation, the author has compared various conventional techniques with his own technique. The complexity has been reduced by just calculating one ICI gain vector and applying the same values to other vectors by the method of constant scaling thus reducing the requirement of IFFT/FFT operation to just 2 pairs. The iterative estimation and cancellation scheme has following steps involved: Decision-Directed channel estimation, Decision-Directed ICI gain estimation, ICI cancellation and finally data detection. The correlation between two ICI gain vector terms is given as:

Cd (Δк)= Е{ Нй (к)Н ∗(к -Δк)} (17)

The comparison has been made between various schemes of cancellation but mainly the prominent comparison is between the linear-approximation and the method suggested by the author. The linear-approximation performs better than the suggested method when index goes away from the diagonal-matrix. So, the method suggested by the author performs better when the value of d is 1, otherwise linear-approximation over-powers the suggested method. But one big advantage of the method is reduced complexity [32]. Apart from this, an improved estimation and ICI cancellation scheme for high-speed scenario have been suggested in [33]. The author has used the concept of Reference Signal (RS) (known at the receiver) to estimate the (CFR). With various pilot-based channel estimation techniques like LS (which doesn’t require channel and noise characteristics and hence results are less accurate), LMMSE (which requires channel and noise characteristics with more accurate results), LMMSE-SVD (Singular Value Decomposition) and Improved algorithm proposed by the author (it focuses on both data position and RS position) teamed up with cancellation schemes, various high-speed scenarios are compared in terms of Mean Square Error (MSE). Improved method gives results that are in coherence with the ideal results. After a certain obtained SNR, throughput becomes stable for all given systems. In a speed range of 0 Km to 500 Km, improved method gives the minimum MSE value and Least Square method gives the maximum MSE value. Same is the case when MSE values of various systems are compared. At an SNR of 20 dB, MSE value given by the improved method is very less. After the application of ICI cancellation method, though the improvement is less but still better results compared to previous results are obtained. At 120 km/h, best MSE results are present whereas at 350 km/h, the results are not very good compared to results for LMMSE method obtained at 120 km/h [33]. As discussed in above few estimation techniques in which CFO estimation is done on the basis of cyclic prefixing, [34] makes use of training symbol. MSEs for CP-based, symbol-by-symbol and Pilot tone based systems at CFO values of 0.15 and 0.30 have been compared. At CFO of 0.15, pilot tone based system gives better results than other two systems whereas at CFO of 0.30, pilot tone based and symbol-by-symbol techniques give almost similar results. This shows that as the CFO value increases, the performance of Pilot based scheme deteriorates and is only visibly better at smaller CFO values. As far as training based scheme is concerned, with increasing value of D (ratio of the OFDM symbol length to the length of a repetitive pattern [34]), MSE performance decreases.

• 5.    Windowing technique

Nyquist window can be used to mitigate ICI produced from carrier frequency offset and additive noise. In [35], author explains how the Nyquist window, that he considers, helps in reduction of amplitude of the filter side lobes. This amplitude is the indication of how safe the Discrete Fourier Transform (DFT) filter bank is, against disturbances and other noises. Sine spurious and frequency deviations lead to reduction of C/N (carrier to noise) ratio. The dwindled side lobes help in C/N improvement of up to 1.3 dB in Gaussian conditions [35].

The Nyquist window using a raised cosine function is given as:

0≤|t|≤(1-α)Τ/2

{                    .| t |     /

_1/2[1-    .||   /

(1-α)Τ/2≤|t|≤(1+α)Τ/2 |t|≥(1+α)Τ

The author has devised a method in which the unaffected guard intervals from the previous OFDM symbols is utilized for tackling the issue of ICI and additive noise. Roll-off factor helps in analysing how the SNR factor improves in case of Nyquist windowing. The value of SNR increases as the roll-off factor increases. The paper shows an improvement of about 1.5 dB when the roll-off factor increases from 0 to 1.

Along with the Constant Nyquist shape, MMSE optimum shape, rectangular shape of conventional OFDM, trapezoidal and raised-cosine shaped Nyquist have been used in [35]. The author has computed the subcarrier SNR against Normalized Frequency Offset (NFO) for all the above said window shapes at an SNR of 10 dB. At NFO value of 0.06, an SNR of about 9.5 dB is obtained by the author for conventional OFDM while for windowing case, he claims that double the value of NFO can be taken by the system [36]. Conventional system’s SNR has been shown to be struck at only 10 dB compared to other systems, while constant shape is claimed to have maximum signal combining gain at NFO of 0. All Nyquist windows considered have a timeaccess factor of 0.266. As this factor approaches 0 or for a smaller factor value, larger part of gain is due to signal combining gain. As this value increases and reaches 1, MMSE is shown to approach the results of the triangular window shape. Similarly as compared to raised-cosine pulse shaped OFDM and better than raised cosine (BTRC) pulse shape OFDM system, [35] shows that rectangular pulse-shaped OFDM has greater ICI power and hence formers are shown to be of better functionality at roll-off factors of 0.2 and 1.

In case of BTRC alone, smaller ICI power smaller by a value of 7.64, at roll-off of 1, is achieved and similarly 0.70 smaller ICI power is achieved at 0.2 [37]. Also, BTRC pulse gives higher SNR when NFO is small but as NFO reaches 0.5, the performance of Raised cosine, BTRC and rectangular window becomes comparable and consequently worsens. Thus increasing the value of roll-off leads to lower ICI. Number of side lobes is directly proportional to the ICI power. Hence if side lobes are more then ICI power in the signal is higher. Increasing the roll-off factor helps in decreasing the side-lobes present in the pulse and hence helps in decreasing the ICI power in the signal.

With a roll-off factor of 0.3 and carrier index of 32, raised cosine, better than raised cosine (BTRC), Second-order continuity window (SOCW) and frank window are compared in terms of ICI power, SIR and BER for 64 – subcarrier QPSK-OFDM [38]. The frank window performs the best as far as smaller ICI power is considered.

SOCW and Frank window pulse are given below:

wℎere0.5+a-^ t +

Pfrank (t)=

{

Psocw (t)= i

a2 t and a2

1- ^| t ^|

Tu

V

1-f (-

-

2|t|1

«Tu a)

(2| ; |-1)

yaT^ a) 0

0.5-

a-^ , and

0≤|t|<

Tu(1-a)

≤|t|<

0≤|t|<^u 2

( l-“)≤|t|

u 2   —          2

Otℎerwise

Tu(1-a) 2

≤|t_|<

^"U,(1+a)

otℎerwise

Tabular comparison with other windows as given in the paper [38] is:

Table 2. Difference values (ICI power) proposed by author in [38] at NFO = 0.1.

Window to be compared with frank’s window	ICI power value (for frank’s window) less than the following values.
Raised – Cosine	2.60 dB
BTRC	1.42 dB
SOCW	0.85 dB

When SIR values for these windows are compared, it is seen that Frank’s window and SOCW give almost the same results at roll-off factors of -0.5 and 1. The SOCW and frank’s window perform better than other three at an NFO value of less than 0.17 but after this value BTRC performs better than other three, though the performance improvement is very minor. Otherwise Frank’s window is shown to outperform all other windows considered by the author in [38].

As an example given by the author in the paper, following table values are cited in [38]. NFO is 0.3.

Table 3. Comparison between BTRC and Frank’s window in terms of ICI power and SIR.

BTRC

1.26 dB lesser ICI power than And

1.01 dB more SIR than

Frank’s window or SOCW

As far as BER is concerned then at roll-offs of 0.3 (NFO = 0.05) and 1 (NFO = 0.15), SOCW outperforms all other windows. As discussed above, roll-off factor directly influences the number of side-lobes, which in turn affects the ICI power in the signal. SOCW is found to have larger side lobes compared to raised-cosine at rolloff of 1 by the author. Hence, two SOCWs with roll-offs of 0.3 and 1 are taken which show a better performance throughout.

Apart from the above-mentioned pulse shapes and windows, Sinc power (SP) pulse and improved Sinc power (ISP) pulse are compared in [39]. Below 20 dB when the additive noise is high, both perform equally good but after this value ISP performs exceptionally well. So, for a larger range of SNR, pulse-shaped OFDM performs much better compared to the conventional OFDM.

• 6.    Conclusion

The paper reviews the four techniques of ICI cancellation. Different techniques have their respective implementation in separate scenarios according to their usage. Though one technique outperforms the other in certain conditions but direct comparison between them cannot be derived as such. If considered separately, Self-cancellation is the simplest technique in terms of implementation. Though implementation is simple, there is definite bandwidth wastage of 50% in this method. Estimation doesn’t cause bandwidth wastage but is comparatively difficult to implement as compared to self-cancellation. However the method is easier than equalization because it doesn’t require any channel statistic information. This is the reason why the results from estimation are not very accurate. Equalization considers the channel information and hence gives more accurate results compared to all other techniques but complexity is the highest in this technique. As far as windowing is concerned, the most important factor that needs to be taken care of is the number and the amplitude of the side lobes. More number of side-lobes directly affect the normalized frequency offset and consequently the ICI power.

This paper is just a deliberate attempt to study the ICI cancellation techniques. The study of various techniques helps in knowing how various techniques and their modifications helped in tackling ICI in OFDM.

Acknowledgements

We would like to thank everyone who helped us in completing this endeavor.