Comparative performance evaluation of entropic thresholding algorithms based on Shannon, Renyi and Tsallis entropy definitions for electrical capacitance tomography measurement systems
Автор: Alfred J. Mwambela
Журнал: International Journal of Intelligent Systems and Applications @ijisa
Статья в выпуске: 4 vol.10, 2018 года.
Бесплатный доступ
The concept of entropy as a measure of information has been extensively applied in information theory and related fields. The complex nature of information has resulted in some proposed entropy definitions. In image processing, the entropy concept has been used in developing thresholding techniques based on maximum entropy principles for image segmentation, enhancement and object detection purposes. In this article, entropy definitions are analysed to establish their relationship and after that evaluate their performance in image thresholding. Static simulated data from Electrical Capacitance Tomography measurement system for annular and stratified flows in multiphase hydrocarbons production has been used. Performance evaluation results of thresholding algorithms using Renyi entropy has shown to improve the measurements, particularly for stratified flow regimes. The improvement is solely based on the entropy definition, and it has been observed the introduced controlling parameters do not affect its performance. Renyi entropic thresholding algorithm is relatively robust as it is independent of the controlling parameter q and the grey level resolution. Therefore, there is the potential possibility of using Renyi entropic thresholding to improve measurements in hydrocarbons flow measurement using Electrical Capacitance Tomography measurement system.
Image segmentation, Thresholding, Entropy, Electric capacitance tomography, multiphase flows
Короткий адрес: https://sciup.org/15016479
IDR: 15016479 | DOI: 10.5815/ijisa.2018.04.05
Текст научной статьи Comparative performance evaluation of entropic thresholding algorithms based on Shannon, Renyi and Tsallis entropy definitions for electrical capacitance tomography measurement systems
Published Online April 2018 in MECS
The Electrical Capacitance Tomography (ECT) is one of the imaging system developed for monitoring and measurement of industrial processes [1-6]. The system has been extensively evaluated for applications in hydrocarbons multi-phase flow measurement and monitoring [7-15]. In this application, one of the requirements for ECT system is to be able to generate at least 100 frames per second. As a result, the most commonly used reconstruction algorithm is the Linear Back Projection (LBP), a crude but simple and fast algorithm suitable for fast flowing industrial processes. However, the problem with the LBP algorithm is that it generates poor quality images, which are mostly used for qualitative analysis only. Improving the quality of the reconstructed images from these systems has attracted the attention of researchers. Some reconstructions algorithms have been proposed to address the problem [16-24]. Others have improved images from LBP by further preprocessing the images using different approaches such as filtering [25], segmentation[26] and curve fitting [27].
One of the investigated image pre-processing segmentation techniques is thresholding [28-31], the simplest method of image segmentation, enhancement and object detection. Entropy-based thresholding techniques have been applied to images generated from ECT system for multiphase flow imaging applications in hydrocarbons industry [26, 32]. However, in their work, only two definitions of entropies as proposed by Shannon [33] and Pal [34] were used with Shannon entropy emerging as relatively better entropy for the application. The problem with the Shannon entropy definition is that it does not guarantee the best generalisation of results, and assume implicit control of trade-offs in the grey level distributions under considerations. A more generalised definition of entropy with the potential of revealing additional unique information and explicit control of the trade-offs between the grey level distributions was desirable to accommodate the existing complexity of the concept of information [35].
Ref.[36], proposed a generalised entropy definition that is an extensive quantity for statistically independent systems. Ref. [37], extended the generalisation of Renyi entropy by adding an extra controlling parameter.
Independently, Ref.[38], proposed another generalised entropy definition that is a nonextensive quantity for statistical mechanics systems. In the case of images, Tsallis entropy assumes the presences of non-additive information in some class of images, not like Renyi. However, Tsallis definition has been shown by ref. [39] to be the un-normalized definition of a previous definition proposed by Havrda and Charvat [40] which was extending the generalisation of Renyi entropy definition.
In this contribution, the evaluation work on entropic thresholding in ECT applications is extended to include other definitions of entropy; the Renyi entropy that generalises the Shannon entropy, the Kapur entropy, which further generalises the Renyi entropy and the Havrda-Charvat-Tsallis entropy for online measurement of the component fraction in the hydrocarbon industry. Results show that both Renyi and Havrda-Charvat-Tsallis entropies produce the same results. The extra controlling parameters introduced in Renyi and Kapur entropies do not influence the performance of the thresholding algorithms. On comparing with the Shannon entropy thresholding algorithms, Renyi entropy thresholding algorithms are flow regime dependent, improving performance for stratified flow regime only. Renyi entropy algorithms are relatively robust as they are grey level resolution independent, a feature that can reduce computation cost.
-
II. Ect Systems
ECT is one of the non-invasive measurement systems for imaging industrial processes. Its goal is to generate instantaneous images of dielectric material component permittivity distributions inside a vessel using external capacitance measurement [41, 42]. The imaging technique is capable of distinguishing between different components or phases in a multiphase mixture based on the permittivity distribution in the mixture.
The ECT system is mainly composed of three subsystems; the sensor, sensor electronics and a computer were image processing take place (see Fig. 1). The focus of this work is on the image processing sub-system, which has three basic functions; to control the sensor electronics, to process capacitance data and to provide the user interface to the system. Processing of capacitance data, in its basic form, involves capacitance data normalisation, image reconstruction from projection and filtering. Thresholding was added to data processing for this work.
-
A. Reconstruction Algorithm.
The reconstruction algorithm has a role of converting measured capacitance data into an image showing the permittivity distribution in a vessel. The commonly implemented reconstruction algorithm is the Linear Back Projection (LBP), which owes its success because it is direct, fast and reasonably simple to implement. A brief theoretical consideration is as follows;
Capacitance and permittivity distribution are related using the equation (1)
C=^=-1^ e(x,y)V0(x,y)dn (1) V V where £ is the permittivity distribution in the sensing field, V the potential difference between two electrodes forming the capacitance, ф the potential difference distribution, and ^ the electrode's surface. In the linearized and discrete state, the LBP reconstructed image grey levels can be represented by the following equation [16].
N
g=z k=1
S T * C k
T Sk
where S is the sensitivity map and C the normalised capacitance vectors.
The reconstruction algorithm has a role of converting measured capacitance data into an image showing the permittivity distribution in a vessel. The commonly implemented reconstruction algorithm is the Linear Back Projection (LBP), which owes its success because it is direct, fast and reasonably simple to implement. A brief theoretical consideration is as follows;
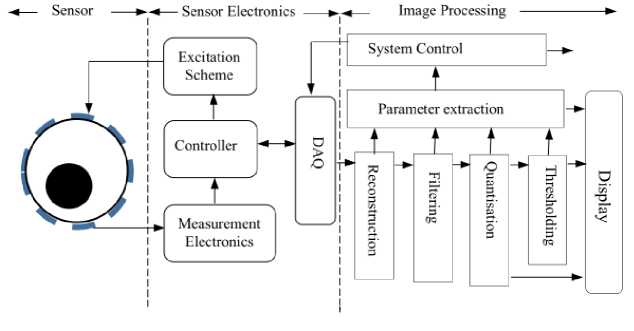
Fig.1. Basic building blocks for an ECT system
-
B. Filtering.
Images generated by LBP reconstruction algorithm, however, are severely blurred. To avoid excessive smoothing and suppress aliasing, filtering is employed in the data after reconstruction [25].
(0
g
k
Sk = \gk S 11 gk > 1 where P = (1- y)«(4) The thresholding value M Y = M 2Cm m =1 Average values of the normalised capacitance N a = N E gn n =1 Average values of the reconstructed permittivity III. Entropic Thresholding. The goal of thresholding is to select a set of optimal thresholding grey levels that can be used to discriminate objects from the background pixels in an image. The selection techniques can be classified into two groups such as bi-level and multi-level. In bi-level thresholding, only one thresholding value is used in thresholding process. The challenge is to develop cost functions that can be derived directly from data without further assumptions to capture as much information as possible within the data probability density function, upon which the selection will be based. Shannon, [43] proposed such cost functions based on an information-theoretic concept of entropy. The principle of entropy is to use uncertainty as a measure to describe the information contained in the image. The maximum information is achieved when no apriori knowledge is available, in which case, it results in maximum uncertainty. Entropy-based thresholding technique considers an image grey levels histograms as the probability distribution, analyse the profile characteristics of the histograms, and then select optimal thresholding grey level values that yield Maximum Entropy (ME). Thresholding techniques using ME as optimal criteria for image thresholding was first introduced by Pun [44], whose theoretical work was corrected and improved by Kapur et al. [45]. Pal and Pal [34] addressed the inadequacy of Shannon’s entropy when it comes to image data by proposing an alternative entropy definition. Generated interest in the work of Kapur et al. [45] has resulted in some thresholding techniques addressing different issues and limitations such as spatial information, entropy correlation, cross entropy and fuzzy logic applications [46]. A comprehensive review can be found somewhere else in the literature [47-49]. The concept of information is so rich that perhaps, there is no single definition that will be able to quantify. Further, estimating entropy from data is in not a trivial matter. Therefore, the information-theoretic approach based on Shannon's entropy concept has received considerable interest resulting in other alternative measures of information or entropy. One of the problems with Shannon's entropy is that it does not guarantee the best generalisation of results, and assume implicit control of trade-offs in the distributions under considerations. Renyi [36] introduced parametric families of entropies as a mathematical generalisation of Shannon’s entropy. Tsallis [38] also did the same albeit from a statistical physics point of view. Both introduced a parameter q in the definition of entropy which offers explicit control of some tradeoffs involved when ME thresholding and help to make the definitions of entropy less sensitive to the shape of the probability distribution. In both cases, it has been shown that when the parameter q → 1, they reduce to Shannon’s entropy. A. Shannon’s Entropy Based Thresholding. According to Shannon [43], the entropy of an image is defined as n HNS =—E Pl ln Pi (7 i=1 Where pt is the probability of occurrence of the Ith grey level and i E [1, n] n the total number of grey-levels. In Kapur et al. [45], also synonymously referred to as Kapur, implementation of the ME thresholding based on Shannon’s entropy, the object and background are considered as separate signal sources and the thresholding grey level that maximises their additive combined entropy is the most optimal one. H (T) = HS (T) + HS (T)(8) H (T) = -£— ln(9) 1=1 Pt Hb (T) =-EE —pi— ln —pi— i =1+'T(1 - Pt ) (1 - Pt ) Topt = arg max [H^ (T) + Hb(Ty](11) B. Renyi’s Entropy Based Thresholding. According to Renyi [36], a more generalised definition of entropy of an image is defined as R n (1—^) ln n Z (Pi)) . i=1 where q * 1 and q > 0. The definition is an extensive quantity for statistically independent sub-systems and has a concave distribution only for 0 < q > 1. It has been shown that Renyi entropy reduces to Shannon entropy as a limiting case when q ^ 1. Kapur [37] extended the generalisation of Renyi entropy by adding another parameter /?. quantity of the systems in statistical mechanics. It is used due to the presence of non-additive information in some classes of images, unlike Renyi entropy.Tsallis entropy reduces to Shannon entropy as a limiting case when q ^ 1. It turns out that this Tsallis entropy is the unnormalized case of a previously reported definition of Havrda and Charvat entropy [40] which was normalised to 1. otherwise, they are essentially the same expressions [39]. HnH {1 -[z ;=/ p) -]} (1 - 21-q) HK = —1—ln n (1 - q) Z „с Pi) q+в-1 Z Pi)в In Albuquerque et al. [52], the first implementation of the ME thresholding based on Tsallis entropy, follow a similar approach as Kapur but replaces the pure addition expression (equation 11) by pseudo-additive expression. where q * 1 and q > 0; /? > 0 and q + /? — 1 > 0. The definition reduces to Renyi entropy when /? = 1. Further, it reduces to Shannon entropy when /? = 1 and as a limiting case when q ^ 1. In this case, the two entropy definitions yield the same results, hence treated as the same. The first use of Renyi entropy in image thresholding was introduced by Sahoo et al. [50]. Their implementation follows a similar approach of maximum entropy as proposed by Kapur (see equation 11). HR (T) = HO (T) + HR (T) + (1 — a)H0 (T)HR (T) hOT (t ) = (q -1) n HT (T) = En n( i=1+T pi 1=1+T X1 - Pt hR(T) = hR(T) + hR(T) (14) (q -1) HR (T) = —1—ln (1 - q) HR (T) = —1—ln (1 - q) n Z i=T+1 _ [ HoO(T) + HO(T)+ 1 To,t argmax [d — ^HoXTXmJ (23) The use of Maximum Entropy principles in these algorithms yields the same results for both Renyi and Tsallis entropic thresholding. It can be shown that the two entropy definitions are monotonic functions of each other [53]. Topt = arg max [HR (T) + HR (T)] (17) HR =Zn[1 + (1 — q)HR](1 — q)-1 (24) As it turns out, this approach makes the entropy correlation approach suggested by Yen et al. [51] its special case when q = 2. C. Tsallis’s Entropy Based Thresholding. Independently, Tsallis (1988) proposed a more generalised Shannon’s entropy of an image defined as HnT {1 -[Z L( Pi)q ]} (q -1) where q * 1 and q > 0. The definition is a non-extensive IV. Methods The main objective of this work was to analyse and evaluate the performance of the suggested thresholding algorithms based on the new definitions of entropies in measuring component volume fraction in a two-components multiphase mixture of oil and gas. After that, compare the results with the previously evaluated Shannon based thresholding algorithms. Computer simulated data were used in the evaluation process to establish static properties of the algorithms under considerations over the full component volume fraction range. Static image and capacitances data were generated from an 8 - electrodes ECT sensor unit simulator [54]. The simulator is capable of generating multi-component permittivity distributions of annular and stratified flows in a circular pipe, herein referred to as true or reference distribution. After that related simulated capacitance measurements were obtained from the capacitance forward problem solver implemented using 2D Finite Element Methods (FEM). These simulated capacitance measurements were used by the capacitance inverse problem solver, also referred to as reconstruction algorithm to try to generate the original true distribution. In this work, the generated images from an ECT system is a result of a combination of signal processing techniques such as image reconstruction, filtering, quantization and thresholding. The LBP is the implemented reconstruction algorithms. Filtering technique as proposed by Xie et al. also referred as Xie has been implemented. Three quantizing resolutions, 16, 256 and 512 have been used for evaluation. Two thresholding techniques based on maximum entropy and maximum correlation thresholding have been used. Entropy definitions by Shannon, Renyi, and Tsallis have been implemented in the ME thresholding, with maximum correlation as a special case of Renyi thresholding implementation. As a result, some algorithms implemented for evaluation, are summarised in table 1. Table 1. Algorithms evaluated and associated abbreviations. Q, X and G stands for quantization, Xie filtering and gas as an object to be searched, respectively. Algorithms Description LBP_XQ Conventional Quantized filtered LBP algorithm. SHA_XG Thresholding algorithm with Shannon entropy REN_XG Thresholding algorithm with Renyi entropy TSA_XG Thresholding algorithm with Tsallis entropy YEN_XG Maximum correlation thresholding algorithm V. Performance Evaluation Criteria. The performance evaluation criteria for the proposed algorithms can be summarised based on accuracy, robustness under the various combination and operating environment and usability to the hydrocarbon industry applications. A. Accuracy. Accuracy refers to the capability of the algorithm to produce reconstructed images close to the original images, both spatially and volumetrically. The similarity metrics used include qualitative visual inspection and quantitative Mean Square Error (MSE) and Gas Volume Fraction Error (GVFE). mH^-^iW) (25) where N is the number of pixels and gt the ith pixel grey level value GVFE = \\aTec-aTef\\ (26) where a = —1—Е;=1 A gt and At the ith pixel area and ^pipe Apipe the total are of the pipe. B. Robustness. The performance of the thresholding algorithms is influenced by; the reconstruction algorithm used, filters applied, the quantizer resolution, the components distribution in the mixture, the object to be searched and flow regime nature. Therefore, robustness refers to the capability of the algorithm to consistently perform over full component volume fraction range and under various combination and conditions. A good algorithm should be independent of the factors mentioned above. C. Usability. Usability refers to practical applicability of the algorithm in measuring component volume fraction of two components multiphase flow in hydrocarbons industry (see Table 2). Table 2. Accuracy requirements for a typical multiphase meter in hydrocarbons production over the full component volume fraction scale [55] Oil Industry Application Desired Volumetric Accuracy Reservoir management Fiscal -Custody transfer Fiscal -Taxation/royalty ~ ± 10% for all flow phases ± 2-5% for all flow phases ± 0.25% for oil ± 2% for water ± 1% for gas VI. Results and Discussion Qualitative evaluation through visual inspection shows clear differences between LBP reconstructed and thresholded images (Fig.2). Further, there is a notable difference between images generated by Shannon and the rest of the entropic thresholding algorithms. Shannon algorithm tends to overestimate the reference images whereas the rest of the entropic algorithm tends to underestimate the reference image, particularly for annular flows. There are no visible differences among Renyi, Tsallis and maximum correlation entropic thresholding unless the quantitative evaluation is considered. Quantitative evaluation using MSE show a relatively poor average performance of the Shannon algorithm to the rest of the entropic thresholding algorithms (Table 3), particularly for annular flows tested. Also, it can be seen, that Renyi, Tsallis and maximum correlation entropic thresholding generates the same MSE results suggesting that they are the same. Maximum cross correlation is a special case of Renyi entropic thresholding (q = 2). Under maximum entropy principle implemented in the thresholding process, Renyi and Tsallis will generate the same results always [53]. As a result, of this, the discussion that follows on algorithms performance evaluation will be focusing on Shannon and Renyi entropic thresholding algorithms only. Quantitative evaluation has been extended to cover the whole component volume fraction range to see a broader picture of the performance of the thresholding algorithms for both annular and stratified flows. Plots of MSE and reference component fraction range have been used for these purposes.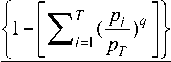
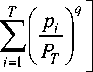
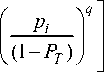
Список литературы Comparative performance evaluation of entropic thresholding algorithms based on Shannon, Renyi and Tsallis entropy definitions for electrical capacitance tomography measurement systems
- Alme K. J, Mylvaganam S. "Electrical capacitance tomography; sensor models, design, simulations, and experimental verification. IEEE Sens J 2006, vol.6, pp. 1256–66. doi:10.1109/JSEN.2006.881409.
- Marashdeh Q, Warsito W, Fan L. S, Teixeira F. L. "A multimodal tomography system based on ECT sensors". IEEE Sens J 2007, vol. 7, pp. 426–33. doi:10.1109/JSEN.2006.890149.
- Marashdeh Q, Fan L. S. "Electrical capacitance tomography - a perspective". Ind Eng Chem Res 2008. vol. 47, pp. 3708–19.
- Yang W. "Design of electrical capacitance tomography sensors". Meas Sci Technol 2010, vol. 21, 042001 (13pp). doi:10.1088/0957-0233/21/4/042001.
- Peng L, Ye J, Lu G, Yang W. "Evaluation of the effect of some electrodes in ECT sensors on image quality". IEEE Sens J 2011, vol. 12 pp. 1554–65. doi:10.1109/JSEN.2011.2174438.
- Seong C. K, Pusppanathan J, Abdul Rahim R, Loon G. C, Susiapan Y.S.L, Phang F.A, et al. "Hardware development of electrical capacitance tomography (ECT) system with capacitance sensor for liquid measurements". J Teknol, 2015, vol. 73, pp 13–22. doi:http://dx.doi.org/10.11113/jt.v73.4399.
- Liu S, Chen Q, Wang H. G, Jiang F, Ismail I, Yang W. Q. "Electrical capacitance tomography for gas-solids flow measurement for circulating fluidised beds". Flow Meas Instrum, 2005, vol. 16, pp. 135–44. doi:10.1016/j.flowmeasinst.2005.02.013.
- Ismail I, Gamio J. C. C, Bukhari S. F. A, Yang W.Q. "Tomography for multiphase flow measurement in the oil industry". Flow Meas Instrum, 2005, vol. 16, pp. 145–55. doi:10.1016/j.flowmeasinst.2005.02.017.
- Li Y, Yang W, Xie C, Huang S, Wu Z, Tsamakis D, et al. "Gas/oil/water flow measurement by electrical capacitance tomography". Meas Sci Technol, 2013, vol. 24, 074001 (12pp). doi:10.1088/0957-0233/24/7/074001.
- Rodriguez Frias M. A, Yang W. "Model-based image reconstruction for electrical capacitance tomography with a prior calculated database". 2016 IEEE Int. Conf. Imaging Syst. Tech., 2016, pp. 350 – 5. doi:10.1109/IST.2016.7738250.
- Nombo J, Mwambela A, Kisangiri M. Performance Analysis of Grey Level Fitting Mechanism based Gompertz Function for Image Reconstruction Algorithms in Electrical Capacitance Tomography Measurement System. Int J Comput Appl 2015;109:8887. doi:dio.10.5120/19263 - 0960.
- Sun J, Yang W. A dual-modality electrical tomography sensor for measurement of gas-oil-water stratified flows. Meas J Int Meas Confed 2015;66:150–60. doi:10.1016/j.measurement.2015.01.032.
- Ismail A. S. I, Ismail I, Zoveidavianpoor M, Mohsin R, Piroozian A, Misnan M. S, et al. Review of oil-water through pipes. Flow Meas Instrum 2015;45:357–74. doi:10.1016/j.flowmeasinst.2015.07.015.
- Rahman N. A. A, Rahim R. A, Nawi A. M, Ling L.P, Pusppanathan J, Mohamad E. J, et al. A Review of Electrical capacitance Tomography Sensor Development. J Teknol (Sciences Eng) 2015;73:35–41.
- Zhou Y. G, Yan H, Fang Z. The design of an Electrical Capacitance Tomography System based on LabVIEW. Int J Signal Process Image Process Pattern Recognit 2015;8:165–78. doi:10.14257/ijsip.2015.8.11.16.
- Yang W, Peng L. Image reconstruction algorithms for electrical capacitance tomography. Meas Sci Technol 2003;14.
- Lei J, Liu S, Li Z. H, Sun M. Image reconstruction algorithm based on the extended regularised total least squares method for electrical capacitance tomography. IET Sci Meas Technol 2008;2:326–36. doi:10.1049/iet-smt:20080029.
- Wu X, Huang G, Wang J, Xu C. "Image reconstruction method for electrical capacitance tomography based on compressed sensing principle". Meas Sci Technol, 2013, vol. 24, 075401 (7 pp). doi:10.1088/0957-0233/24/7/075401.
- Cao Z, Xu L. "Direct methods for image reconstruction in electrical capacitance tomography" Ind. Tomogr., 2015, doi:10.1016/B978-1-78242-118-4.00014-9.
- Ye J, Wang H, Yang W. "Image reconstruction for electrical capacitance tomography based on sparse representation". IEEE Trans Instrum Meas 2015, vol. 64, pp. 89–102. doi:10.1109/TIM.2014.2329738.
- Cui Z, Wang Q, Xue Q, Fan W, Zhang L, Cao Z, et al. "A review of image reconstruction algorithms for electrical capacitance/resistance tomography". Sens Rev, 2016, 36. doi:http://dx.doi.org/10.1108/SR-01-2016-0027.
- Nombo J, Mwambela A, Kisangiri M. "A review of image reconstruction methods in electrical capacitance tomography". J Math Comput Sci, 2016, vol. 6, pp. 39–57.
- Yang Y, Peng L, Jia J. "A novel multi-electrode sensing strategy for electrical capacitance tomography with ultra-low dynamic range". Flow Meas Instrum, 2017, vol. 53, pp. 67–79. doi:10.1016/j.flowmeasinst.2016.05.005.
- Rodriguez Frias MA, Yang W. "Real-time model-based image reconstruction with a prior calculated database for electrical capacitance tomography". Meas Sci Technol, 2017, vol. 28, 4006. doi:10.1088/1361-6501/aa6221.
- Xie CG, Huang SM, Beck MS, Hoyle BS, Thorn R, Lenn C, et al. "Electrical capacitance tomography for flow imaging: system model for the development of image reconstruction algorithms and design of primary sensors". IEE Proc G (Circuits, Devices Syst), 1992, vol. 139, pp. 89–98.
- Mwambela AJ, Johansen G. "Multiphase flow component volume fraction measurement: Experimental evaluation of entropic thresholding methods using an electrical capacitance tomography system". Meas Sci Technol, 2001, vol. 12, 1092–101. doi:10.1088/0957-0233/12/8/315.
- Nombo J, Mwambela A, Kisangiri M. "A Grey Level Fitting Mechanism based on Gompertz Function for Two Phase Flow Imaging using Electrical Capacitance Tomography Measurement". Int J Comput Appl, 2014, vol. 101, pp. 7–12. doi:dio.10.5120/17705 - 8704.
- Bhatia P., Singh S, Kumar V. "On Applications of a Generalized Hyperbolic Measure of Entropy". Int J Intell Syst Appl, 2015, vol. 7, pp. 36–43. doi:10.5815/ijisa.2015.07.05.
- Ye Z. W, Wang M. W, Liu W, Chen S Bin. "Fuzzy entropy based optimal thresholding using bat algorithm". Appl Soft Comput J 2015, vol. 31, pp. 381–95. doi:10.1016/j.asoc.2015.02.012.
- Ye Z, Wang M, Jin H, Liu W, Lai X. "An Image Thresholding Approach Based on Ant Colony Optimization Algorithm Combined with Genetic Algorithm". Int J Intell Syst Appl, 2015, vol. 7, pp. 8–15. doi:10.5815/ijisa.2015.05.02.
- Sadek S. Entropic Image Segmentation : A Fuzzy Approach Based on Tsallis Entropy. Int J Comput Vis Signal Process, 2015, vol. 5, pp. 1–7.
- Mwambela A, Isaksen Ø, Johansen G. "The use of entropic thresholding methods in the reconstruction of capacitance tomography data". Chem Eng Sci, 1997, vol. 5, pp. 2149–59. doi:https://doi.org/10.1016/S0009-2509(97)00041-9.
- Shannon C. E. "A mathematical theory of communication". Bell Sys Tech Jr, 1948, 27:379-423-659.
- Pal NR, Pal SK. "Entropic thresholding". Signal Processing 1989, vol. 16, pp. 97–108.
- Maszczyk T, Duch W. "Comparison of Shannon, Renyi and Tsallis entropy used in decision trees". Lect Notes Comput Sci (Including Subser Lect Notes Artif Intell Lect Notes Bioinformatics) 2008, 5097 LNAI, pp. 643–51. doi:10.1007/978-3-540-69731-2_62.
- Rényi A. "On measures of entropy and information". Entropy 1961, vol.47, pp. 547–561. doi:10.1021/jp106846b.
- Kapur J. N. "Generalized entropy of order α and type β". Maths Semi 1967, vol. 4, pp. 79–84.
- Tsallis C. "Possible generalisation of Boltzmann–Gibbs statistics". J Stat Phys 1988, vol. 52, pp. 480–7.
- Sahoo P. K, Arora G. "Image thresholding using two-dimensional Tsallis–Havrda–Charvát entropy". Pattern Recognit Lett, 2006, vol. 27, pp. 520–8. doi:http://dx.doi.org/10.1016/j.patrec.2005.09.017.
- Havrda J, Charvát F. "Quantification method of classification processes: Concept of structural a-entropy". Kybernetika 1967, vol. 3, pp. 30–5.
- Wang F, Marashdeh Q, Fan LS, Warsito W. "Electrical capacitance volume tomography: Design nd applications." Sensors 2010, vol. 10, pp. 1890–917. doi:10.3390/s100301890.
- Marashdeh Q, Fan L. S, Du B, Warsito W. "Electrical Capacitance Tomography − A Perspective". Ind Eng Chem Res 2008, vol. 47, pp 3708–19. doi:10.1021/ie0713590.
- Shannon, C. E. "A Mathematical Theory of Communication". Bell System Tech J 1948, vol. 27, pp. 379–423.
- Pun T. "Entropic thresholding, a new approach". Comput Graph Image Process 1981, vol. 16, pp. 210–39.
- Kapur J. N, Sahoo P. K, Wong A. K. "A new method for gray-level picture thresholding using the entropy of the histogram". Comput Vision, Graph Image Process 1985, vol. 29, pp. 273–85. doi:10.1016/0734-189X(85)90125-2.
- Yin P. Y. "Multilevel minimum cross-entropy threshold selection based on particle swarm optimisation". Appl Math Comput 2007, vol. 184, pp. 503–13.
- Sahoo P., Soltani S, Wong A. K. "A survey of thresholding techniques". Comput Vision, Graph Image Process 1988, 41, vol. 23, pp. 3–60. doi:10.1016/0734-189X(88)90022-9.
- Sezgin M. "Survey over image thresholding techniques and quantitative performance evaluation". J Electron Imaging, 2004, vol. 13(1), pp. 146-165.
- Chang C. I, Du Y, Wang J, Guo S. M, Thouin P. D. "Survey and comparative analysis of entropy and relative entropy thresholding techniques". IEE Proc Vis, Image Signal Process 2006, vol. 153, pp. 837–50. doi:10.1049/ip-vis.
- Sahoo P, Wilkins C, Yeager J. "Threshold selection using Renyi’s entropy". Pattern Recognit 1997, vol. 30, pp. 71–84. doi:10.1016/S0031-3203(96)00065-9.
- Yen J. C, Chang F. J, Chang S. "A new criterion for automatic multilevel thresholding". Image Process IEEE Trans 1995, vol. 4, pp. 370–8.
- Portes de Albuquerque M, Esquef I. A, Gesualdi Mello A. R, "Image thresholding using Tsallis entropy". Pattern Recognit Lett, 2004, vol. 25, pp. 1059–65. doi:10.1016/j.patrec.2004.03.003.
- Johal R. S, Tirnakli U. "Tsallis versus Renyi entropic form for systems with q-exponential behaviour: the case of dissipative maps". Phys A Stat Mech Its Appl 2004, vol. 331, pp. 487–96. doi:10.1016/j.physa.2003.09.064.
- Isaksen Ø. "A novel approach to reconstruction of process tomography data". PhD. Thesis, University of Bergen, 1994.
- Hjertaker B.T. "Static characterization of a dual sensor flow imaging system". Flow Meas Instrum 1998, vol. 9, pp. 183–91. doi:10.1016/S0955-5986(98)00018-1.


