Comparative Study of Firefly Algorithm and Particle Swarm Optimization for Noisy Non-Linear Optimization Problems
Автор: Saibal K. Pal, C.S Rai, Amrit Pal Singh
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 10 vol.4, 2012 года.
Бесплатный доступ
There are various noisy non-linear mathematical optimization problems that can be effectively solved by Metaheuristic Algorithms. These are iterative search processes that efficiently perform the exploration and exploitation in the solution space, aiming to efficiently find near optimal solutions. Considering the solution space in a specified region, some models contain global optimum and multiple local optima. In this context, two types of meta-heuristics called Particle Swarm Optimization (PSO) and Firefly algorithms were devised to find optimal solutions of noisy non-linear continuous mathematical models. Firefly Algorithm is one of the recent evolutionary computing models which is inspired by fireflies behavior in nature. PSO is population based optimization technique inspired by social behavior of bird flocking or fish schooling. A series of computational experiments using each algorithm were conducted. The results of this experiment were analyzed and compared to the best solutions found so far on the basis of mean of execution time to converge to the optimum. The Firefly algorithm seems to perform better for higher levels of noise.
Metaheuristic Algorithm, Firefly Algorithm, PSO, Noisy Non-Linear Optimization
Короткий адрес: https://sciup.org/15010318
IDR: 15010318
Текст научной статьи Comparative Study of Firefly Algorithm and Particle Swarm Optimization for Noisy Non-Linear Optimization Problems
Published Online September 2012 in MECS
In combinatorial optimization (CO) [2], algorithms can be categorized as either complete or approximate algorithms. Complete algorithms are guaranteed to find for every finite size instance of a CO problem an optimal solution that exists in bounded time. Still, for CO problems that are NP-hard, no polynomial time algorithm exists, assuming that P! = NP. Thus, complete methods might need exponential computation time in the worst-case scenario. This often leads to computation times that are usually too high for being useful in practical purposes. In approximate methods such as metaheuristics [1,2] we compromise on the guarantee of finding optimal solutions just for the sake of getting good solutions in a notably reduction in the amount of time. Thus, the use of metaheuristics has been receiving considerable attention in the last 3 decades. This was also the case in the continuous optimization; due to other reasons: metaheuristics are usually easier to implementation as compared to classical gradient-based techniques [2]. Moreover, metaheuristics do not require any gradient information. This is convenient in the case of optimization problems where the objective function is only implicitly given (e.g., when objective function values are acquired by simulation), or here the objective function is not differentiable [2,3]. Two major components of any metaheuristic algorithms are namely intensification and diversification, or exploitation and exploration. Diversification simply means the generation of diverse solutions so as to explore the search space on the global scale, while by intensification the meaning here is to focus on the search in a local region by the exploitation of the information that a currently good solution is found in this region. This is combined with the selection of the best solutions [1].
In this paper we are using two metaheuristic algorithms - PSO and Firefly algorithm for providing solutions. In 1995, significant progress was made towards development of the Particle Swarm Optimization (PSO) [11,10] technique by American social psychologist James Kennedy, and engineer Russell C. Eberhart. Loosely speaking, PSO is an optimization algorithm which is inspired by swarm intelligence of the fish and birds and even by human behavior. These multiple agents called particles which swarm around the search space starting from some initial random guess. Firefly Algorithm (FA) [1,4,9]
was developed by Xin-She Yang at Cambridge University in 2007. FA is an optimization algorithm inspired by the behavior and motion of fireflies.
This paper aims to compare the firefly algorithm with PSO for solving noisy non-linear problems. Rest of the paper is organized as follows. The Firefly and PSO algorithms are briefly explained and noisy non-linear mathematical models to be used for experimentation are explained in Section 2. Experimental settings and results are then presented in section 3. Section 4 finally concludes the paper.
-
II. Metaheuristics & Optimization
-
2.1. Firefly Algorithm
-
2.1.1. Behavior of Fireflies
-
-
2.1.2. Concept
Now we can idealize some of the flashing characteristics of fireflies so as to develop firefly-inspired algorithms. Flashing characteristics of fireflies is used to develop firefly-inspired algorithm. Firefly Algorithm (FA or FFA) [1,4,9] developed by Xin-She Yang at Cambridge University in 2007, use the following three idealized rules:
The sky filled with the light of fireflies is a marvelous sight in the summer in the moderately temperature regions. There are near to two thousand firefly species, and most of them produce short and rhythmic flashes. The pattern observed for these flashes is unique for most of the times for a specific species. The rhythm of the flashes, rate of flashing and the amount of time for which the flashes are observed are together forming a kind of a pattern that attracts both the males and females to each other. Females of a species respond to individual pattern of the male of the same species.
We know that the intensity of light at a certain distance r from the light source conforms to the inverse square law. That is the intensity of the light I goes on decreasing as the distance r will increase in terms of I α 1/r2. Additionally, the air keeps absorbing the light which becomes weaker with the increase in the distance. These two factors when combined make most fireflies visible at a limited distance, normally to a few hundred meters at night, which is quite enough for fireflies to communicate with each other.
-
• All the fireflies are unisex so it means that one firefly is attracted to other fireflies irrespective of their sex.
-
• Attractiveness and brightness are proportional to each other, so for any two flashing fireflies, the less bright one will move towards the one which is brighter. Attractiveness and brightness both decrease as their distance increases. If there is
no one brighter than other firefly, it will move randomly.
-
• The brightness of a firefly is determined by the view of the objective function.
-
2.1.3. Light Intensity And Attractiveness
For a maximization problem, the brightness is simply proportional to the value of the objective function. Other forms of the brightness could be defined in an identical way to the fitness function in genetic algorithms.
In the firefly algorithm, there are two important points: the variation in the light intensity and formulation of the attractiveness. For simplicity, we can assume that the attractiveness of a firefly is determined by its brightness which in turn is connected with the encoded objective function.
In the simplest case for maximum optimization problems, the brightness I of a firefly for a particular location x could be chosen as I(x) f(x). Even so, the attractiveness β is relative, it should be judged by the other fireflies. Thus, it will differ with the distance rij between firefly i and firefly j. In addition, light intensity decreases with the distance from its source, and light is also absorbed by the media, so we should allow the attractiveness to vary with the varying degree of absorption. In the simplest form, the light intensity I(r) varies according to the inverse square law.
I(r)=> (1)
Where I s is the intensity at the source. For a stated medium with a fixed light absorption coefficient γ, the light intensity I varies with the distance r. That is
I=Ioе " уг (2)
Where Io is the initial light intensity, In order to avoid the singularity at r = 0 in the expression^-, the combined effect of both the inverse square law and absorption can be approximated as the following Gaussian form.
I=Io e " yr 2 (3)
Since a firefly’s attractiveness is proportional to the light intensity seen by adjacent fireflies, we can now define the attractiveness β of a firefly as в=во e“ yr 2 (4)
Where β0 is the attractiveness at r = 0. Since it is often faster to calculate1/(1 + r2) than an exponential function, the above function, if necessary, can be approximated as
βo в (1 +уr2) (5)
Both (4) and (5) define a characteristic distance Г=1/γ over which the attractiveness is changing significantly from βo to βoe-1 for equation (4) or βo/2 for equation (5). In the real time implementation, the attractiveness function β(r) can be any monotonically decreasing functions such as the following generalized form
в(г)=во e"yrm (m >=1).(6)
For a fixed, the characteristic length becomes
Г=γ-1/m → 1, m → ∞.(7)
Conversely, for a specific length scale Г in an optimization problem, the parameter γ can be used as a typical initial value. That is
-
Y = £(8)
The distance between any two fireflies i and j at x i and x j , respectively is the Cartesian distance.
-
n j = ||^ - xi l| = J^iC^-^y
Where X t, k is the kth component of the spatial coordinate xi of ith firefly In 2-D case, we have
П,i = 7 (Xt - xiY - (Yt - YiY
The movement of the firefly i is attracted to another more attractive (brighter) firefly j is determined by
Xt = Xt + во e-vriJ2 (Xi - X)) + a€,
Where the second term is due to the attraction and third term is randomization with α being the randomization parameter, and € , is a vector of random numbers being drawn from a Gaussian distribution or uniform distribution. For example, the simplest form is €i could be replaced by (rand - ½) where rand is a random number generator uniformly distributed in [0, 1]. For most of our implementation, we can take βo=1 and α Є [0, 1].
It is worth pointing out that (11) is a random- walk partial towards the brighter fireflies. If β o = 0, it becomes a simple random walk. Furthermore, the randomization term can easily be prolonged to other distributions such as L´evy flights [1].
The parameter γ now characterizes the contrast of the attractiveness, and its value is crucially important in determining the speed of the convergence and how the FA algorithm behaves. In theory, γ Є [0, ∞), but in actual practice, γ= O(1) is determined by the characteristic length Г of the system to be optimized. Thus, for most applications, it typically varies from 0.1 to 10. The firefly algorithm is given below.
FFA Meta-heuristic()
Begin;
Initialize algorithm parameters:
MaxGen: the maximal number of generations γ: the light absorption coefficient
-
r: the particular distance from the light source
-
d: the domain space
Define the objective function of f(x), where x=(x1,........,xd)T
Generate the initial population of fireflies or xi (i=1, 2 ,..., n)
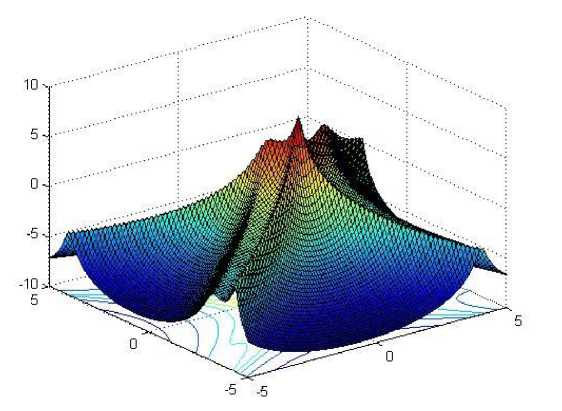
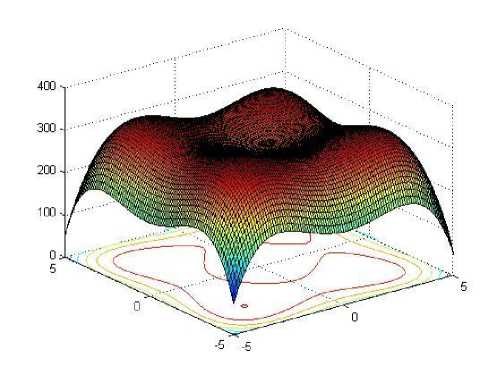
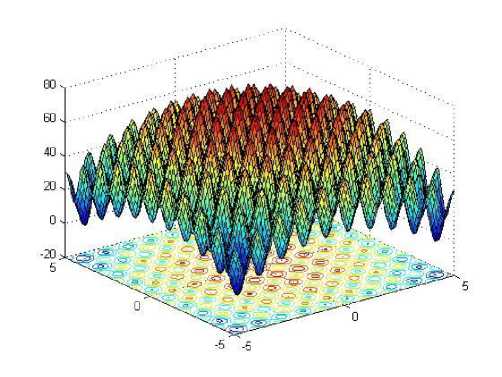
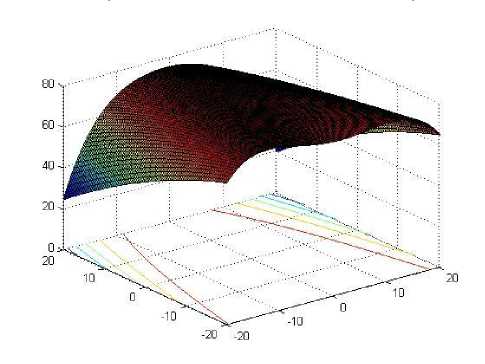
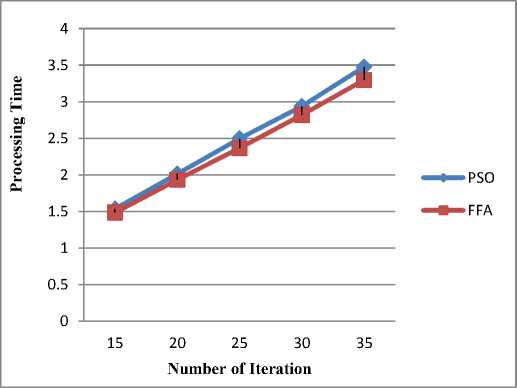
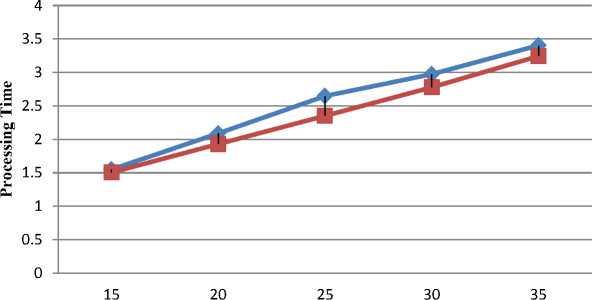
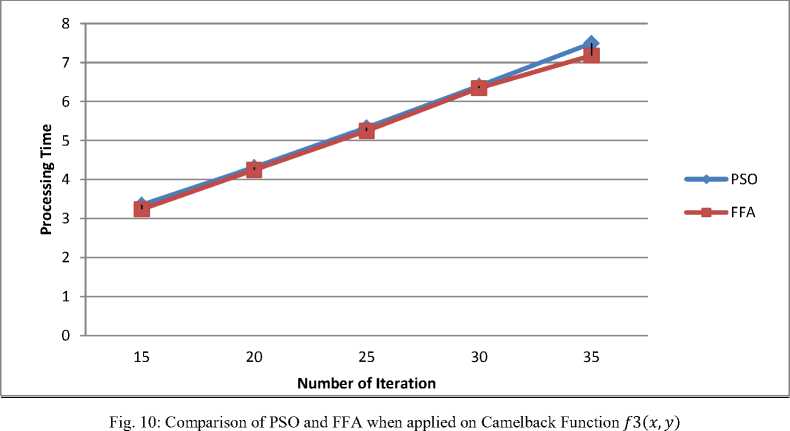
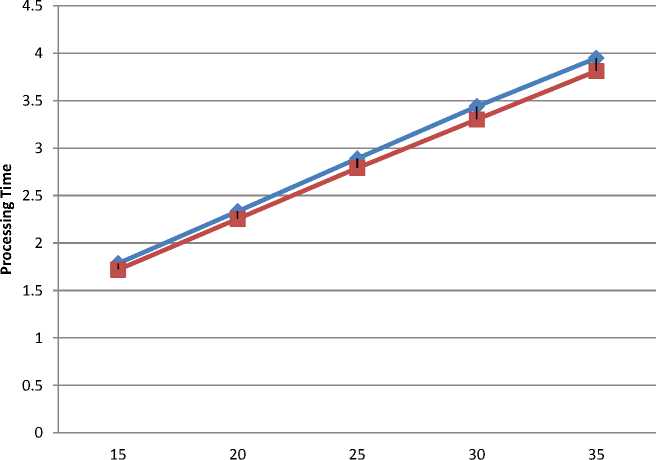
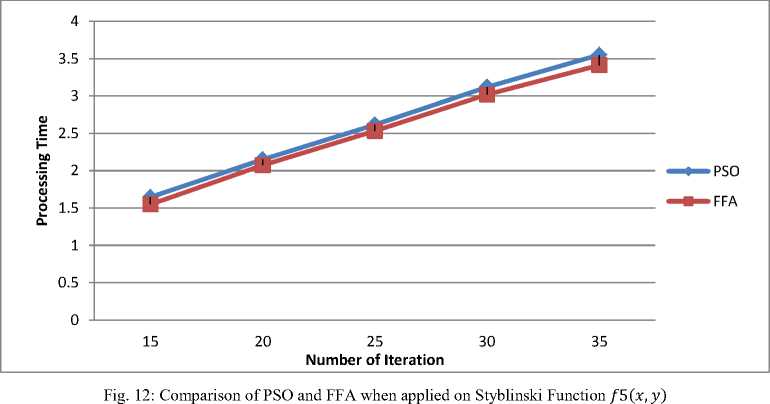
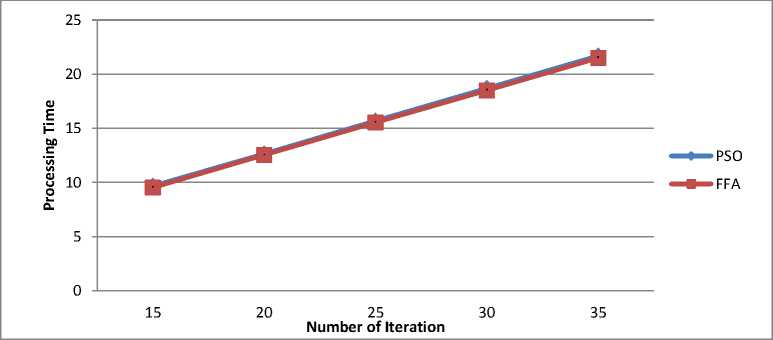
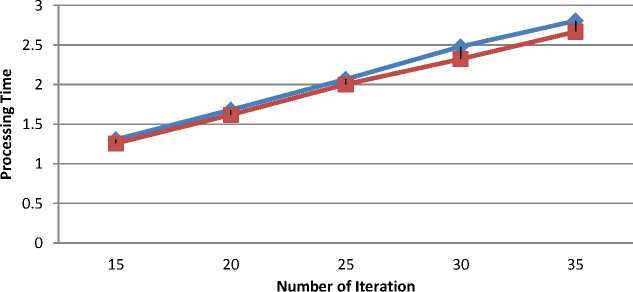
Determine the light intensity of Ii at xi via f(xi) While (t For i = 1 to n (all n fireflies); For j=1 to n (n fireflies) If (Ij> Ii), move firefly i towards j by using 11 equation; end if Attractiveness varies with distance r via Exp [-γr2]; Evaluate new solutions and update light intensity; End for j; End for i; Rank the fireflies and find the current best; End while; Post process results and visualization; End procedure 2.2. Particle Swarm Optimization Algorithm Particle swarm optimization has been used to solve many optimization problems Developed by Kennedy and Eberhart in 1995 [11]. A population based 2.2.1. PSO Algorithm optimization technique inspired by social behavior of bird flocking or fish schooling, PSO consists of a swarm of particles. Each particle resides at a position in the search space. The fitness of each particle represents the quality of its position. The particles fly over the search space with a certain velocity. The velocity (both direction and speed) of each particle is dependent on its own best position found so far and the best possible solution that was found so far by its neighbors. Eventually the swarm will converge to optimal positions by using (12) and (13) equation. The PSO algorithm is as follows: Randomly initialize particle positions and velocities While not terminate • For each particle i: • Evaluate fitness yi at current position xi • If yi is better than pbesti then update pbesti and pi • If yi is better than gbesti then update gbesti and gi For each particle i: • xi is a vector denoting its position and yi denotes its objective function value • vi is the vector denoting its velocity • pi is the best position that it has found so far and pbesti denotes its objective function score Comparative Study of Firefly Algorithm and Particle Swarm Optimization for Noisy Non-Linear Optimization Problems • gi is the best position that has been found so far in its neighborhood and gbesti denotes the objective function value of gi For each particle update velocity vi and position xi using: 6 *rand(pi-zL) rand (p?-zL) 411 = w ^+----■;■*---(12) 3.3. Camelback Function Consider seven non-linear mathematical models without constraints (taken from [5]). Considering the solution space in a certain region of 2D response surfaces, some models contain global optimum and multiple local optimums as described below. 3.1. Four Peak function Fig. 3: 2D Matlab plot for Camelback Function Fig. 1: 2D Matlab plot for four peak function 3.4. Goldstein-Price Function {(1+(11X1 y)2(l9-14z 13X2 -14y 16zy 13у2)) } 3.2. Parabolic Function Fig. 2: 2D Matlab plot for Parabolic Function ( 30+(2z- 3 y)2(l 8 - 32 X112 X2148у - 36 zy 127 у 2 ) Fig. 4: 2D Matlab plot for Goldstein-Price Function 3.5. Styblinski Function Г/x4 - 16x2 + 5x y4 - 16y2+ 5 f5(x,y) = 275 - [(-----2-----) + (^----2^) + 3J Fig. 5: 2D Matlab plot for Styblinski Function 3.6. Rastrigin Function f 6(x,y) = 80 - [20 + x2 + у2 - 10(cos(2^x) + cos(2ny))] Fig. 6: 2D Matlab plot for Rastrigin Function f(x,y) N PSO FFA /Клу) 15 1.5356 1.4840 20 2.0135 1.9326 25 2.4959 2.3652 30 2.9367 2.8186 35 3.4758 3.2951 /2(х,у) 15 1.5482 1.5039 20 2.0884 1.9296 25 2.6466 2.3504 30 2.9733 2.7769 35 3.4039 3.2429 /3(х,у) 15 3.3491 3.2372 20 4.3162 4.2481 25 5.3308 5.2477 30 6.3998 6.3473 35 7.4936 7.1793 /4(х,у) 15 1.7848 1.7189 20 2.3342 2.2550 25 2.8904 2.7896 30 3.4392 3.3023 35 3.9492 3.8121 /5(х,у) 15 1.6444 1.5478 20 2.1504 2.0725 25 2.6144 2.5323 30 3.1201 3.0196 35 3.5502 3.4115 /6(х,у) 15 9.6761 9.5298 20 12.6412 12.5404 25 15.6878 15.5457 30 18.6878 18.4993 35 21.6923 21.4953 /7(х,у) 15 1.3076 1.2575 20 1.6808 1.6187 25 2.0679 2.0029 30 2.4794 2.3223 35 2.8054 2.6684 Table-1.Processing time in second for both algorithms applied on seven noisy non-linear mathematical models. 3.7. Rosenbrock Function f 7(x,y) = 70 [|20-{(1--7)1 + ((6)*(-7),У}]*150] + 10 Fig. 7: 2D Matlab plot for Rosenbrock Function Fig. 8: Comparison of PSO and FFA when applied on Four Peak function /1(x,y) Number of Iteration PSO FFA Fig. 9: Comparison of PSO and FFA when applied on Parabolic Function f2(x , y) Number of Iteration PSO FFA Fig. 11: Comparison of PSO and FFA when applied on Goldstein-Price Function /4(x,y) Fig. 13: Comparison of PSO and FFA when applied on Rastrigin Function /6(x, )) Fig. 14: Comparison of PSO and FFA when applied on Rosenbrock Function /7(x,y) Figure 14 shows comparative study of both algorithms on the basis of different noisy non-linear mathematical model (X-axis represents number of iterations and Y-axis represents time to process). IV. Conclusion And Future Work When there was no noise on the process yields, the performance of both algorithms PSO and FFA seems to be not so different to approach to the optimum. FFA tends to be better, especially on the functions having multi-peaks. Complexity or difficulty level of the functions had no effect to the FFA as expected except on the Camelback function. However, execute time in each replication is dramatically higher when they are compared, especially on the functions having a curved ridge or mixed curved ridge and multi-peak. PSO seems to be better in terms of speed of convergence. This might be due to the effect from generating the completely different random numbers to be used in the iterative procedures of the algorithm. This implies that the FFA is potentially more powerful in solving noisy non-linear optimization problems. The FFA seems to be a favorable optimization tool in part due to the effect of the attractiveness function which is a unique to the firefly behavior. The FFA not only includes the self improving process with the current space, but it also includes the improvement among its own space from the previous stages. Also Firefly is better than PSO in terms of the time taken for the optimum or near optimum value to be generated provided certain high level of noise where the difference in time taken becomes more evident with the increase in the level of noise shown in table 1. Firefly algorithm has some disadvantage such as getting trapped into several local optima. Firefly algorithm performs local search as well and sometimes is unable to completely get rid of them. Firefly algorithm parameters are set fixed and they do not change with the time. In addition Firefly algorithm does not memorize or remember any history of better situation for each firefly and this causes them to move regardless of its previous better situation, and they may end up missing their situations. In future, we would like to use multiple variants of firefly algorithm such as, Gaussian distribution for random walk [4]. The chaos enhanced firefly algorithm for tuning of parameter α, β and γ [9, 10] seems to be a good idea to us for solving practical problems in information and network security.f 3(x,y) = 10 - Zoy (x2 - (4 -
+ xy + 4y2(y2
2.1x2 + (1) x4)
-1))
4+1 = 4 + a t* 411
III. Noisy Non Linear Mathematical Functions
f 1(x,y) = e-(z- 4) -(у-4)2+ е-(^4)2-(у-4)2 + 2[e-x2 - y2+e-x 2-(y14)2]
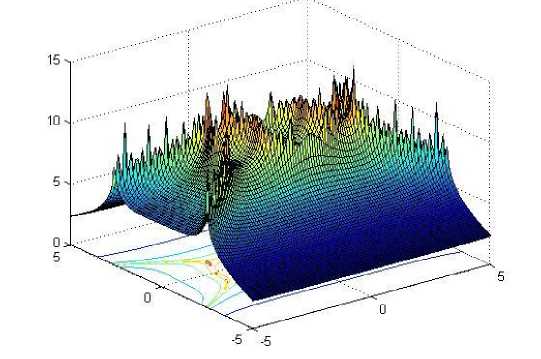
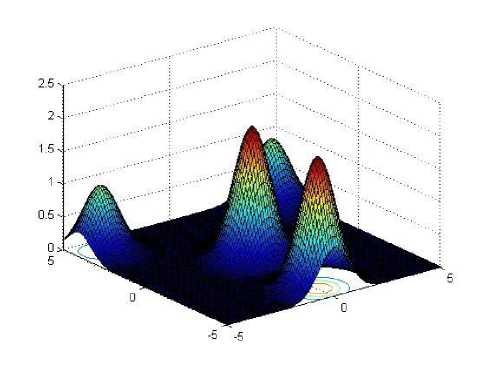
/4(x,y) =
10 + Zoy [
*
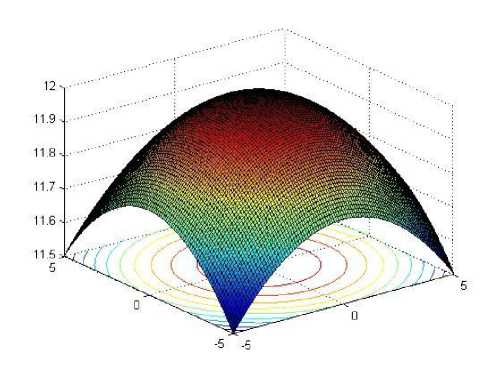
f 2(x,y) = 12 - (x2 + y 2 )/100
Список литературы Comparative Study of Firefly Algorithm and Particle Swarm Optimization for Noisy Non-Linear Optimization Problems
- X. S. Yang, “Nature-Inspired Metaheuristic Algorithms”, Luniver Press, 2008.
- Christian Blum, Maria Jos´e Blesa Aguilera, Andrea Roli, Michael Sampels, Hybrid Metaheuristics, An Emerging Approach to Optimization, Springer, 2008 .
- WengKee Wong, Nature-Inspired Metaheuristic Algorithms for Generating Optimal Experimental Designs, 2011.
- Sh. M. Farahani, A. A. Abshouri, B. Nasiri, and M. R. Meybodi, “A Gaussian Firefly Algorithm”, International Journal of Machine Learning and Computing, Vol. 1, No. December 2011.
- N. Chai-ead, P. Aungkulanon, and P. Luangpai- boon, Member, IAENG, “Bees and Firefly Algorithms for NoisyNon-Linear Optimization Problems” Inter- national Multiconference of Engineers and Computer Scientists, 2011.
- Hajo Broersma “Application of the Firefly Algorithm for Solving theEconomic Emissions Load Dispatch Problem, ”Hindawi Publishing Corporation, International Journal of Combinatorics, Volume 2011.
- Rania Hassan, Babak Cohanim, Olivier de Weck, A Comparison of the Particle Swarm Algorithm and the Genetic Algorithm, published by AIAA, 2004.
- Bajeh, A. O., Abolarinwa, K. O., A Comparative Study of Genetic and Tabu Search Algorithms, International Journal of Computer Applications, 2011.
- Xin-She Yang, Chaos-Enhanced Firefly Algorithm with Automatic Parameter Tuning, International Journal of Swarm Intelligence Research, December 2011.
- Xiang-yin Meng, Yu-long Hu, Yuan-hang Hou, Wen-quan Wang, The Analysis of Chaotic Particle Swarm Optimization and the Application in Preliminary Design of Ship”, International Conference on Mechatronics and Automation, August, 2010.
- J. Kennedy, R. C. Eberhart, “Particle swarm optimization”, IEEE International Conference on Neural Networks, Piscataway, NJ., pp.942-1948, 1995.


