Comparing Some Pseudo-Random Number Generators and Cryptography Algorithms Using a General Evaluation Pattern

Published Online September 2016 in MECS DOI: 10.5815/ijitcs.2016.09.04

Nowadays, pseudo-random sequences are used in a variety of areas like simulation, game design, modeling, communication channels, especially cryptography and are quite versatile. In recent years, there has been a lot of research in the field of pseudo-random number generation, some focused on using chaotic maps for cryptographic purposes. Some of these researches are reviewed in the following. In [1], authors have improved the Chaotic Tent Map and have shown that the output sequence is completely appropriate. In [2] and [3], a pseudo-random sequence for cryptographic purposes has been designed in such a way that pseudo-random sequences have been generated by using chaotic systems and perturbation and by choosing least significant bits (LSB’s).In [4] and [5], chaotic maps have been used to design a cryptographic algorithm; furthermore, output sequence has been statistically analyzed and method has also been evaluated in term of vulnerability to a variety of attacks, which has proved the security of algorithm. In [6], a new pseudorandom number generator based on a complex number chaotic equation has been introduced and randomness of the produced sequence has been proven by NIST tests. In [7], authors have sought to generate a pseudo-random sequence using discrete chaotic dynamical systems and have proven the validity of produced sequence. In [8], authors have introduced a block cipher using standard chaotic map and have assessed confusion and diffusion in order to evaluate the randomness; they have also assessed the manner of key generation and have carefully conducted sensitivity analysis on output and complexity analysis on the algorithm.

Given the generation of a good pseudo-random sequence as a requirement for a cryptography algorithm, investigation method, evaluation and correct selection is very important in this step. Since nowadays many pseudo-random sequences and cryptography algorithms are being modeled and used, how a good algorithm is investigated is quite essential. Generally, this area can be divided into two parts of pseudo-random sequences whose goal is not cryptography and those whose goals is cryptography. In fact, in case of generation of a good pseudo-random sequence and demonstration of its security for the practical use in spite of its restrictions, it is introduced as a cryptography algorithm. The cryptography algorithms that are used for creation of privacy can be divided into two groups of symmetrical and asymmetrical. Symmetrical algorithms are themselves divided into two groups of block and stream type, all of which are able to generate pseudo-random sequences. It can be said that, all codes are good pseudorandom number generators but its reverse is not true. The goal is that each algorithm, having been designed, can receive a certificate for the approval of suitability for privacy applications. In order to certify an algorithm, actions should be based on a definite and standard framework. In this paper, using the model introduce in paper [9], various algorithms are investigated. In this model, at first the algorithm speed is compared and then in case of passing the stage, a thorough search space of the algorithm is investigated for its breaking. Then, in the next step, the first level of NIST tests are suggested for individual sequences and the algorithm is studied from sensitivity viewpoint. It means that with the smallest changes in input parameters, extensive changes should be observed in the output sequence and this feature is also called Strict Avalanche Criterion [10]. Having passed these stages, various attacks are done on the selected algorithm in accordance with the type of algorithm. In case of resistance against the attacks, the second level of NIST is tested on the algorithm output in which for a large number of sequences, the ratio of sequences that are successful in the tests are compared with the expected ratios. In case of success in this stage, the third level of tests is investigated. In the previous two levels, the comparison is made based on P-value, while in the third level, assessments is done based on uniformity of distribution of P-values. If the number generator passes this stage too, in the last step, the algorithm output is assessed using the repeated logarithm law test.

After the introduction, this paper deals with classification and concise introduction of types of algorithms in the second section. In the third section, the results obtained from implementation of 13 considered algorithms and execution of all steps of the comprehensive model of assessment on them are proposed. In the fourth section, the conclusion and summary is dealt with.

• II.    Various Studied Algorithms

Since all cryptographers are good pseudo-random sequences, a variety of cryptographers can be introduced as good pseudo-random sequences. However, it is worth mentioning that every pseudo-random number generator cannot be used as a cryptography algorithm. In this paper, we have used three types of algorithm that are described briefly next.

• A.    Pseudo-random Number Generators

  Pseudo-random number generator is a deterministic algorithm that receives an input called seed and generates a longer sequence that seems random, meaning that its output is composed of an unidentifiable uniform computational sequence. This group of algorithms is more used for the design of a variety of cryptographers than being suggested a scriptographers themselves. In addition, they have many applications in other areas such as simulation. Among them, Mersenne Twister, various types of linear modular arithmetic number generators, chaotic maps based number generators like Skew tent, CCCBG and MT19937 can be mentioned.

In paper [11], the way of investigating cryptography algorithms designed based on chaotic maps has been investigated and an appropriate model has been proposed to analyze this group of algorithms, which include various types of analyses and attacks.

In paper [12], the chaotic mapping based on CrossCoupled Chaotic Tent Map Based Bit Number generator is introduced and presented, which in fact is the modified form of Skew tent, so that a better behavior in generation of a pseudo-random sequence can be achieved. In this paper, weakness of the Skew tent algorithm is shown using statistical tests of NIST and in order to improve it, the selected interval is changed using α value and also a combination of two Skew tents and definition of a nonlinear relation is used to generate a pseudo-random sequence.

In paper [13], the linear modular arithmetic number generator is introduced and how a pseudo-random sequence is generated by the algorithm is expressed. In paper [14], Mersenne Twister’s pseudo-random number generator is introduced and how the pseudo-random sequence is generated by the number generator is accurately expressed.

• B.    Block Ciphers

In this type of cipher, before performing the cryptography operation, the input data are arranged in blocks with constant lengths and then the cryptography operation is done on them. Length of input and output blocks is the same. The block cipher system can be assumed as a big codebook dependent on a key, such that each input block corresponds to an output block according to the key. In execution, the cryptography operation normally consists of a number of displacements and replacements which depend on the key that is repeated periodically in several cycles.

This group of algorithms encrypts the data according to the block length and its output can be considered as a good pseudo-random sequence. Given the limited length of blocks for block ciphers and very lower length of message than cryptographers block length, the cryptography mode was introduced. In standard condition, five standard modes namely Electronic Codebook (ECB), Cipher Block Chaining (CBC), Cipher Feedback (CFB), Output Feedback (OFB) and Counter (CTR) have been introduced for data privacy and using cryptography modes such as OFB and CTR block ciphers can be transformed to stream ciphers and then, the generated sequence can be XORedwith a private message. In fact, in order to generate the pseudo-random sequence the two mentioned modes are used. AES, DES, SKIPJAC and CAST-256 can be mentioned as block ciphers.

In paper [15], the DES algorithm is introduced and its design method is accurately presented. The DES algorithm is among symmetrical cryptography block algorithms with the block length of 64 bits and the key length of 56 bits. In paper [16], the cryptography analysis of the DES algorithm is performed and the differential attack on the DES algorithm is expressed. For full procedure DES, 247 main texts and its corresponding encrypted text are necessary to be broken completely, while in practice, having such number of messages is almost impossible. Thus, it can be said that the algorithm is operationally robust against the attack.

In paper [17], the AES algorithm is introduced as a symmetrical block cryptography algorithm. The algorithm has a block length of 128 bits and keys length of 128, 192 and 256 bits with procedures of respectively 10, 12 and 14 whose operation is of byte type. In addition, it should be mentioned that the algorithm is a versatile algorithm which is used for privacy.

In [18], the SKIPJAC algorithm has been introduced. This is considered as a block type of algorithm with the block length of 64 bit and key length of 80 bits. Low speed in cryptography and low key length is among the weaknesses of the algorithm.

In [19], the CAST-256 algorithm has been introduced. This is a block type of algorithm with the block length of 128 and a variable key length of respectively 128, 160, 192, 224 and 256. Low speed in cryptography is among the weaknesses of the algorithm.

• C.    Stream Ciphers

Stream ciphers are such that a good pseudo-random sequence as well as secure from cryptography perspective is generated and then an output sequence with a private message is XORed bit by bit. Most of stream ciphers are designed based on good pseudo-random number generators or a part of them consists of these number generators. The most important feature of the algorithms is their high speed with regard to block ciphers. RC4, Frogbit, F-FCRS-8 and Triviumis among the stream ciphers. In [20], various types of stream ciphers is introduced and the studies conducted on the proposed algorithms are expressed and the best algorithms for operational use are introduced.

In paper [21], the RC4 algorithm is introduced. The algorithm is a stream cipher algorithm with a variable key length, whose one of applications is Wireless Cryptography Protocol (WEP).

In paper [22], the Salsa20 algorithm has been introduced. This is a cryptography type of stream algorithm with the key length of 256 bits whose design structure is based ARX and has a good quality in terms of speed and security.

III.    Implementation of the Assessment Model on Algorithms

Diverse criteria have been proposed in valid references to assess the algorithms. In the comprehensive evaluation model reference that comprises various criteria such as statistical tests, implementation attacks and observations are suggested. In this model, eight steps have been considered as the priorities of the comprehensive assessment. In this section, besides implementing the 13 algorithms, we use the mentioned model for them

• A.    The First Step: Speed

Speed is regarded as one of the most important parameters of a good algorithm. The higher the speed of an algorithm, the more is its applications in various areas. It should be mentioned that speed of algorithms is different on hardware and software. As an example, the DES algorithm has a higher speed on the hardware than the software.

• B.    A Thorough Search

  In some algorithms like block and stream types of algorithms, since security is based on the key, the key space for a thorough search is very important. In addition, the algorithm structure should suffer no weaknesses so that the key space doesn’t get limited. Furthermore, other initial condition or input parameters can be considered as the key for determination of the number generator space in pseudo-random number generators. In this stage, condition for the success of the algorithm is the search of a space of more than 2128 [23].

• C.    The First Level of NIST

  In this stage, given the statistical tests on the output sequence, some analyses are conducted to diagnose its randomness. At the first level, a simple test is in fact done on the output to make sure of its randomness. For example, at first, various types of NIST tests are done on 1000000 bits an in case of passing, its second and third level can be investigated. In fact, the other two levels are accomplished because of more randomness of the pseudo-random sequence .

Table 1. Comparison of Algorithms’ Speed

TYPE of ALGORITHM	NAME of ALGORITHM	SPEED QUALITY	PASS or REJECT
Block Cipher	AES256	Good	PASS
Block Cipher	DES	Good	PASS
Block Cipher	CAST-256	Slow	FAIL
Block Cipher	SKIPJAC	Slow	FAIL
Stream Cipher	F-FCRS-8	Good	PASS
Stream Cipher	Frogbit	Good	PASS
Stream Cipher	RC4-like	Good	PASS
Stream Cipher	Salsa20	Good	PASS
Stream Cipher	Trivium	Good	PASS
PRNG	CCCBG	Good	PASS
PRNG	MT19937	Good	PASS
PRNG	PHP-MT	Good	PASS
PRNG	Standard C LCG	Good	PASS

• D.    Sensitivity analysis

Sensitivity analysis is different in different algorithms. However, the general goal is to see if for the smallest changes in the algorithm input there will be considerable changes in the output sequence. It means whether at least half of bits change with regard to the previous state [24].

The higher and more chaotic the changes, the more robust will be the algorithm against sensitivity analysis.

In paper [25], a statistical analysis is performed on stream ciphers algorithms in the synchronous mode. Algorithms are compared in terms of correlation between the key and output sequence, initial value and output sequence, frames correlation and diffusion and it is shown that some algorithms suffer weaknesses in this type of sensitivity analysis.

In paper [10], the SAC test is introduced so that the strict avalanche criterion in algorithms is analyzed. Design and investigation of output sequences using the test has also been introduced.

Table 2. Comparison of robustness against the thorough search attack

TYPE of ALGORITHM	NAME of ALGORITHM	Key Space	PASS or FAIL
Block Cipher	AES256	2256	PASS
Block Cipher	DES	2^6	FAIL
Stream Cipher	F-FCRS-8	-7 126	PASS
Stream Cipher	Frogbit	^128	PASS
Stream Cipher	RC4-like	variable > 2128	PASS
Stream Cipher	Salsa20	2256	PASS
Stream Cipher	Trivium	2 30	PASS
PRNG	CCCBG	variable > 2128	PASS
PRNG	MT19937	variable > 212a	FAIL
PRNG	PHP-MT	variable > 2128	PASS
PRNG	Standard C LCG	variable > 2128	PASS

As an example, in block and stream type of ciphers, changing the key and initial value as well as comparison of output sequences the analysis is carried out. However, in pseudo-random number generators, the analysis is conducted by changing input values as well as comparison of output sequences.

The tests were performed on 1000 sequences with a length of 1000000 bits and for all algorithms, such that in each stage, a comparison is done for block and stream algorithms in terms of correlation between the key and output sequence, initial value and output sequence, frames correlation and diffusion. However, for pseudorandom number generators, the correlation between the seed and output sequence, correlation of different seeds, correlation of frames and also diffusion were compared. In addition, in other algorithms, the SAC test was investigated whose final results are shown in table 4.

• E.    Types of attacks

In this stage, taking into account the type of an algorithm, various types of attacks started to find weaknesses and reduce the search space or even separate output sequences from other pseudo-random sequences. Attacks include heuristic guess and determine attack which is mostly usable for stream ciphers [26]; differential and linear attack, which are mostly used for block ciphers and algorithms with the S_BOX structure and also the differentiation attack that is used to separate the output sequence of an algorithm from other algorithms and statistical tests investigations are among them.

It should be mentioned that various attacks have been designed for cipher analysis such as Related-Key, Boomerang, Biclique etc.

In paper [27], the existing weakness of the algorithm

RC4-like is mentioned and the attacks that are implementable on the algorithm are expressed. One of the most significant weaknesses of the algorithm is on the differentiation attack. It means the output of the algorithm can be separated from other good sequences in an acceptable volume. However, from cryptography analysis perspective, it has numerous weaknesses such as having many weak keys.

In paper [28], the differentiation attack has been introduced. In fact, the very basic goal of this type of attack is to separate linear and non-linear outputs of various number generators.

The most important attack investigated in this stage on other algorithms is the differentiation attack and the results of investigations are shown in table 5.

• F.    The Second Level of NIST

  In this stage, the test NIST is performed on more output sequences of number generators. It means, for instance, NIST tests are investigated on 1000 sequences of 1000000 bits and based on a certainty level of α=0.01, values Р — value > 0.01 are passed. If m and n are respectively assumed as the number of sequences selected for each test and the number of passed sequences and we divide n by m and call the result as k and determine an interval according to equation (1), then if k value is less than the k value calculated in accordance with equation (1), the sequence is rejected for this test. In fact, it can be said that the second level of NIST has not been passed .

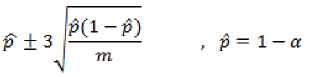
• G.    The Third Level of NIST

In this stage, the distribution of quantities of P-value are observed and calculated for each test and in case of distribution uniformity of all P-value quantities of the existing tests of NIST, it can be said that the number generator has well passed the third level. In figures (1) and (2) for example, the process of passing or rejecting the stage can respectively be seen.

Table 3. Comparison of Final Results of NIST Tests

TYPE of ALGORITHM	NAME of ALGORITHM	NIST
Block Cipher	AES256	PASS
Stream Cipher	F-FCRS-8	PASS
Stream Cipher	Frogbit	PASS
Stream Cipher	RC4-like	PASS
Stream Cipher	Salsa20	PASS
PRNG	CCCBG	FAIL
PRNG	MT19937	PASS
PRNG	PHP-MT	PASS
PRNG	Standard C LCG	PASS

NIST test are given as an example for AES256 [29].

• H.    Iterative Algorithm Law Test

  This test was introduced by Wang in 2015, which is used for the accurate study of pseudo-random sequences as a new test known as the iterative algorithm law test [30]. The purpose of the test is to use the iterative logarithm law that is ignored in NIST test, in which various distances are used for comparison instead of calculation of P-value. The test has been calculated and compared for all the algorithms based on the paper standard.

Table 4. Investigation of sensitivity analysis for the selected algorithms

TYPE of ALGORITHM	NAME of ALGORITHM	Quality Sensitivity	PASS or FAIL
Block Cipher	AES256	Good	PASS
Stream Cipher	F-FCRS-8	Bad	FAIL
Stream Cipher	Frogbit	Bad	FAIL
Stream Cipher	RC4-like	Good	PASS
PRNG	MT19937	Good	PASS
PRNG	PHP-MT	Good	PASS
PRNG	Salsa20	Good	PASS
PRNG	Standard C LCG	Good	PASS

Table 5. Situation of the selected algorithms against various attacks

TYPE of ALGORITHM	NAME of ALGORITHM	Against Attack	PASS or FAIL
Block Cipher	AES256	Resistant	PASS
Stream Cipher	RC4-like	Weak	FAIL
Stream Cipher	Salsa20	Resistant	PASS
PRNG	MT19937	Resistant	PASS
PRNG	PHP-MT	Resistant	PASS
PRNG	Standard C LCG	Resistant	PASS

In fact, the point should be mentioned that the second and third levels are investigated in the attacks section. As a matter of fact, the investigations are normally conducted for the differentiation attack and in table 5, one of the reasons for penetrability in the algorithm RC4 is the weakness against the differentiation attack. Moreover, the results of the

Table 6. Situation of the selected algorithms against the LIL test

TYPE of ALGORITHM	NAME of ALGORITHM	Against LIL	PASS or FAIL
Block Cipher	AES256	Resistant	PASS
Stream Cipher	Salsa20	Resistant	PASS
PRNG	MT19937	Resistant	PASS
PRNG	PHP-MT	Weak	FAIL
PRNG	Standard C LCG	Weak	FAIL

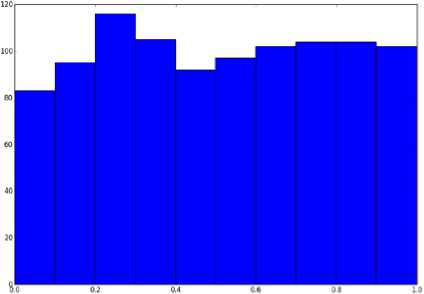
Fig.1. Uniform distribution of quantities of P-value

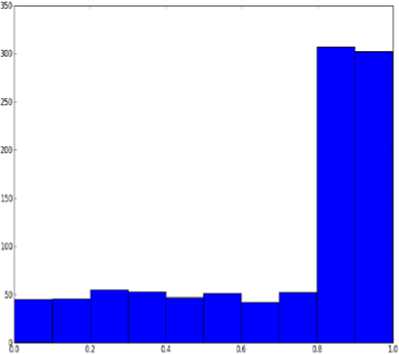
Fig.2. Non-uniform distribution of quantities of P-value

IV.    Conclusion

As was seen, using the model it is possible to analyze different algorithms at an acceptable period of time. Furthermore, the selected path for investigation of algorithms is very important because if the stages are not arranged properly and in order, it will lead to in vain investigations and reduction of accuracy of algorithms analysis. It should be mentioned that if a stage is eliminated or ignored in this model, it may lead to errors in the diagnosis of a good algorithm. The weakness reveals itself clearly especially when the goal is to generate a cryptography algorithm and causes many weaknesses to appear in the algorithm. Thus, it can be said that the most important application of the model is making a new algorithm. In contrast, it is also useful for analyzing different algorithms and it is worth mentioning that the model can be used to give the privacy certificate to an algorithm. In addition, we can imagine what features a good algorithm should have to observe privacy issues. In this paper, having investigated a number of pseudo-random number generators as well as block and stream ciphers, it was demonstrated what weaknesses each one has and in fact, avoiding any excess of analysis, the algorithm was eliminated from the list so that the best one is selected using the model. It should be pointed out that algorithms that pass all the stages well can receive the privacy certificate according to the model. Based on the conducted studies, algorithms AES256, MT19937 and Salsa respectively as a block cryptographer, a pseudorandom number generator and a stream cryptographer have passed all the stages and can be given the privacy certificate in accordance with the model.