Comparison of Mamdani Fuzzy Inference System for Multiple Membership Functions

Published Online September 2016 in MECS

Image enhancement technique is a process that gives an output image which is more suitable for analysis of a specific application like Medical, Satellite images, Military, Print Media. It is broadly classified in two categorize, spatial domain and frequency domain. In Frequency domain, image enhancement is mainly based on Fourier transform and the Spatial domain is based on pixels manipulation of an image. Due to fast computation, efficiency, and less processing resources, spatial domain technique is more suitable as equivalence to other methods. Image enhancement has classified in the spatial domain as brightness control, contrast enhancement, noise reduction and edge enhancement. Apart from other methods, contrast enhancement method is used to remove noise and contrast improvement from given image to enhance the image for faster interpretation and analysis.

Image enhancement methods are also known as Contrast enhancement methods, which is mainly used three basic types of functions negative and identity transformation, log and inverse-log transformation, and nth power and nth root transformations. These functions are used to remove noise, improve visibility and increase contrast to enhance the image for proper analysis and interpretation [5, 6].

In spite of these two domains, one more domain has been described recently to enhance images in various enhancement applications which are known a fuzzy domain. A fuzzy domain is based on fuzzy sets of fuzzy logic methods. Fuzzy logic methods able to handle vague and unclear difficulties by using expert knowledge and represent knowledge as a powerful tool to mimic human reasoning. Fuzzy sets are used to make rules to make machine just like as human perception [7, 8]. Fuzzy contrast technique is used for better enhancement of images without increasing the noise which is present in input image [9]. This method is also applicable to low contrast images [10]. This kind of fuzzy techniques based on fuzzy rule-based model also known as IF-THEN rules by using different membership functions [11]. Enhancements of images are also effective and flexible by using fuzzy sets in fuzzy rule-based techniques [12].

Two types of fuzzy inference system (FIS) models are presented to better determine the image contrast enhancement of gray-scale image based on attributes such as the number of IF-THEN rules, different membership functions (MFs), fuzzy contrast factor [13, 14, 15].

In Fuzzy Theory, there are two types of available fuzzy Rule-based models namely non-additive and additive rule model. The non-additive rule based model is also known as Mamdani fuzzy inference system (Mamdani FIS) while additive rule based model is known as Takagi-Sugeno fuzzy inference system (Sugeno FIS) [2, 3, 4]. The main differences between these two FIS are as follows. (i) Sugeno FIS requires less number of rules as compared to Mamdani FIS, (ii) the computation required for defuzzification would be less in Sugeno FIS than Mamdani FIS because output membership function is not used in Sugeno FIS during defuzzification and the resultant output would be weighted average.

Sugeno FIS uses simple IF-THEN rules and incorporates these rules based on human reasoning rather than a complex mathematical model. Thus, Mamdani FIS is widely used due to intuitive nature of rule base. Sugeno FIS is computationally efficient and well suited to work with optimization and linear techniques. Crisp input values are obtained from given input image and it is then converted into fuzzy values using the input MFs [1]. Followings are the generalized MFs used in this paper.

• 1.    Trapezoidal Membership function ( М- ( z ) ) =

• 2.    Bell Membership function

  ( м(z))=

  
  

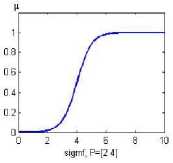
• 4.    Sigmoid Membership function( Sigmoid ( X , а , с ))

• 5.    Triangular Membership Function

  
  
  
  
  
  

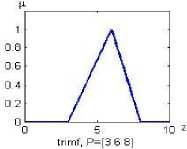
  µ(z) =

  
  
  

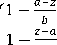
  а- b ≤ z < а^

  а ≤ Z ≤ а + с >

  
  

  0     ot ℎ erwise

  
  

а-z

⎧1-        а-с≤z< а

^⎪   1 ^c        а≤z< b

1- ^z-b    b≤z≤b+d

⎩   0          Otherwise

{ (z;С- b , с -, с )

1- S ( z ; с , с _{+ ,} с + b )

3. Gaussian Memebrship

function ( Gaussian ( X : , о ))

Z ≤ с

Z > с

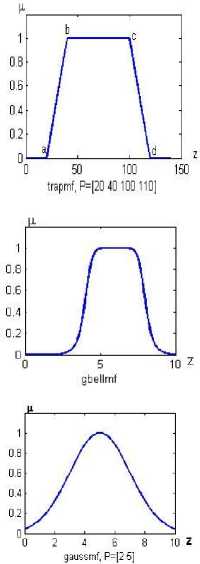
( X - т )

=    {- о² }

= ₁₊ е ^а(  )

• II.    Fuzzy Rule Base Fis Design

The fuzzy contrast factor plays an important role in the enhancement of contrast for low contrast images. Here challenges are the use of the potential of fuzzy rule-based approach and different MFs for the analysis of the image using Mamdani FISs.

Fuzzy rule base will be a fuzzy partitioning for input and output domains. These rules base would be generated automatically utilizing the available local image-specific information.

In this paper, Comparison of Mamdani methods has been given on the basis of image qualitative attributes of contrast enhancement of images and resultant images. Following contributions of this paper are:

• a.    We propose FIS using different types of MFs for contrast enhancement and detailed analysis of Rule-base system is presented.

• b.    We perform an evaluation of different MFs based FIS against the    state-of-the-art    fuzzy

enhancement techniques, based on different types of Rule-base design.

• c.    We describe the study of the interaction of input MFs and output MFs in the design of Rule-base for FIS.

• d.    We explore the potential of Rule-base design according to human perception in fuzzy based image enhancement algorithms.

Major headings should be typeset in boldface with the first letter of important words capitalized.

• III. Evolution and Performance Attributes

In Contrast enhancement technique quality of images can be different as per human perception. Here a description of different quality attributes has been given. On the basis of these quality attributes we can compare the better appearance of images.

Various performance attributes are following:

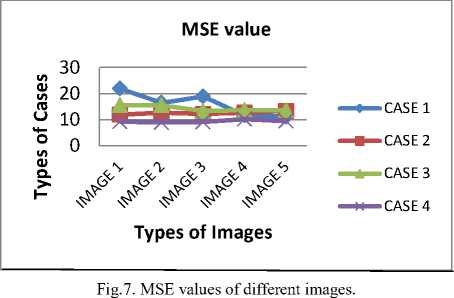
• A.    Mean Square Error (MSE)

MSE =    ∑ о" 1 ∑О 1 ⃒⃒f(i,j) –д(i,j) ⃒⃒(1)

• B.    Peak Signal-To-Noise Ratio (PSNR)

PSNR = 10Log10(s )(2)

• C.    Index of Fuzziness (IOF)

I(A) = (2/nk). d (A, Ã)(3)

Where d(A, Ã) denotes between fuzzy set A and its nearest ordinary set Ã.

Here we have taken four different cases in which different combinations of membership functions are selected. On the basis of different quality values shown in all tables, image quality will be better for the higher value of PSNR and a smaller value of MSE. For evaluations, given input images are shown in figure (1) and their results are given in tables 1, 2, 3, and 4.

• IV.    Experimental Studies

Here four cases are taken on the basis of multiple membership functions of FIS. Following input images are taken for evaluation of result:

й^^^^,.	^^^'	w^; m™ huw »В ’ S^M нЧ1/ jMM ■■■ l a ВЩ^ й
IMAGE 1	IMAGE 2	IMAGE 3   IMAGE 4   IMAGE 5

Fig.1. input images

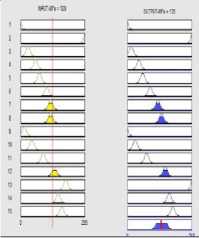
A. CASE 1

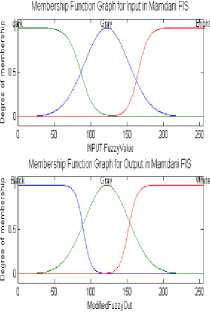
This case is based on three combinations of Sigmoid shaped membership function and Gaussian membership function. Below figure (2) is showing input and output membership functions and their rules.

Table 2. Fifteen combinations of MFs.

	MSE	PSNR	INDEXOF FUZZINESS(IOF)
IMAGE 1	11.8767	37.3839	-0.018303
IMAGE 2	12.691	37.0959	-0.19751
IMAGE 3	12.1918	37.2701	-0.028699
IMAGE 4	12.6703	37.1029	0.088304
IMAGE 5	13.3171	36.8867	-0.19621

C. CASE 3

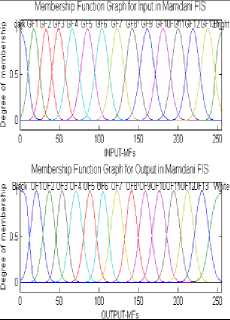
This case is based on nineteen combinations of Sigmoid shaped membership function and Gaussian membership function. . Below figure (4) is showing input and output membership functions and their rules.

MFs

Rules

Fig.2. Three Membership functions and their rules.

Table 1. Three combinations of MFs

Input Image	MSE	PSNR	INDEX     OF FUZZINESS(IOF)
IMAGE 1	21.914	34.7236	-0.095621
IMAGE 2	16.4304	35.9743	-0.23182
IMAGE 3	18.8913	35.3682	-0.086661
IMAGE 4	11.6534	37.4663	0.013683
IMAGE 5	11.1306	37.6656	-0.24024

B. CASE 2

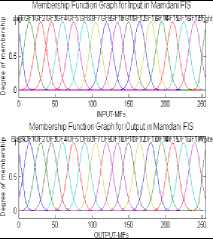
This case is based on fifteen combinations of Sigmoid shaped membership function and Gaussian membership function. Below figure (3) is showing input and output membership functions and their rules.

Membership Funci on Graph for Input in Mamdani FIS s йжшшттткжтрттажсяптттшж

И»

rOFH^HBFiraiFW

О1ГТР1ЯМГ5

О 50          100         150         200         250

INPUT-ffs Membership Function Graph for CUput in Mamdani FIS

MFs

Rules

MFs

Rules

Fig.4. Nineteen Membership functions and their rules.

Table 3. Nineteen combinations of MFs.

	MSE	PSNR	INDEX OF FUZZINESS(IOF)
IMAGE 1	15.6427	36.1877	-0.046542
IMAGE 2	15.4997	36.2276	-0.17714
IMAGE 3	13.3168	36.8868	-0.057898
IMAGE 4	13.6592	36.7766	0.063421
IMAGE 5	13.6356	36.7841	-0.2315

D. CASE 4

This case is based on Twenty-six combinations of Sigmoid shaped membership function and Gaussian membership function. Below figure (5) is showing input and output membership functions and their rules.

MFs

Rules

Fig.5. Twenty-six Membership functions and their rules.

Fig.3. Fifteen Membership functions and their rules.

Table 4. Twenty-six combinations of MFs.

	MSE	PSNR	INDEX     OF FUZZINESS(IOF)
IMAGE 1	9.2052	38.4905	-0.047048
IMAGE 2	8.9364	38.6192	-0.23403
IMAGE 3	9.1023	38.5393	-0.050318
IMAGE 4	10.1939	38.0474	0.07282
IMAGE 5	9.4377	38.3821	-0.23225

On the basis of above statistics, we can compare quality and contrast of images. Higher the PSNR and lower the MSE value shows the better contrast of images. Index of fuzziness (IOF) gives indistinctness present in an image. The lower value of the index of fuzziness will proceed for better enhancement.

PSNR Value

V. Results and Discussions

On the basis of images and graph, following observations show the comparison and clearly gives the visual aspect of images.

Types of Images

♦  CASE 1

— ■ —CASE 2

*  CASE 3

CASE 4

CASE 1

CASE 2

CASE 3

CASE 4

Input image

Fig.6. Different cases for Original and Enhanced Images.

Fig.8. PSNR values of different images.

Index of Fuzziness

• CASE 1 — ■ — CASE 2 —*— CASE 3      CASE 4

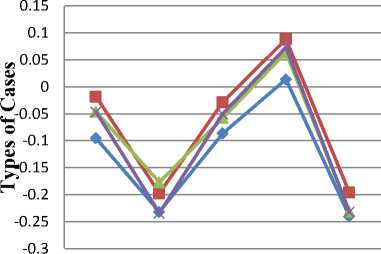
Types of Images

Fig.9. Index f Fuzziness values of different images.

VI. Conclusions and Future Work

This paper demonstrates a combination of multiple membership functions to optimize contrast enhancement of input image and produced an output image with better contrast as compared to the input image. Results and analysis show that FIS is a power tool for presenting the image in a better way. As a future scope more combination of membership functions introduced for better analysis and enhanced image.