Computer Modeling of Magnetic Properties of Disordered BCC Phase of Fe100-xMex Alloys (Me = Al, Ga, Ge)

The scientific community's interest in the research and development of multifunctional iron-based materials is constantly growing. The demand for environmentally friendly materials makes these alloys especially attractive. The unique combination of mechanical, magnetic, and electrical characteristics of Fe- Me alloys ( Me = Al, Ga, Ge) with high magnetostriction values in low magnetic fields [1, 2] is of particular interest for researchers and makes such alloys promising for the creation of sensors and actuators and other magnetomechanical devices. The ability to convert magnetic energy into mechanical energy and vice versa allows these alloys to be used in industry, power engineering, automotive engineering, and other areas. Thus, studies of Fe- Me alloys ( Me = Al, Ga, and Ge) remain relevant both from the point of view of fundamental science and practical application. This is confirmed by the constant growth in the number of publications in this field.

Experimental studies show that addition of nonmagnetic elements such as aluminum, gallium, or germanium into α-Fe with a body-centered cubic ( bcc ) lattice allows for a significant increase in the magnitude of tetragonal magnetostriction in the resulting alloys compared to pure iron [2]. The phase diagrams of the Fe_{100- x}Me_x systems ( Me = Al, Ga, Ge) in the concentration range from 0 to 10 at. % reveal the presence of a disordered bcc structure A 2 (symmetry group no. 229, Im -3 m , with α-Fe as prototype). In this case, similar behavior of parameters such as tetragonal magnetostriction and the Curie temperature is observed. In the single-phase A 2 region, a gradual decrease in Curie temperature T_C is observed, which becomes sharper during the formation of the D 0₃ structure. This is accompanied by the appearance of a two-phase region, which affects the magnetic characteristics of the material [3].

The theoretical calculation of the transition temperature from ferromagnetic (FM) to paramagnetic (PM) state, presented in [4–7], showed an interesting feature of the obtained results. A complex approach using ab initio calculations and Monte Carlo modeling reveals a decreasing behavior of the T C ( x )

Физика curve dependences in the Fe100-xAlx, Fe100-xGax, and Fe100-xGex alloys only in the concentration range of x > 12 at. %. However, in the region of lower concentrations, the behavior of the curve cannot be reproduced, since studies show the opposite trend: the Curie temperature increases with a change in the concentration of Me = Al, Ga, Ge from zero to 12 at. %. The authors explain this behavior by an increase in the exchange interaction Jij between iron atoms, as well as an increase in the magnetic moment of Fe atoms μFe. It is important to note the observed correlation between the values of Jij and μFe and the lattice parameter: the larger the lattice parameter, the stronger the exchange interaction and the greater the magnetic moment per iron atom [5, 6]. Thus, the obtained results indicate a complex relationship between the structure, composition, and magnetic properties of Fe100-xMex alloys (Me = Al, Ga, Ge), which opens up new prospects for basic research into the mechanisms of forming magnetic properties in these materials.

In this paper, we analyze the influence of the crystal lattice parameter and the concentration of nonmagnetic atoms of Me = Al, Ga, Ge on the exchange interaction, as well as the Curie temperature of the A 2 structure of Fe 100- x Me x alloys (0 ≤ x ≤ 14 at. %) using ab initio simulation.

• 1.    Calculation details

• 2.    Results and discussion

To simulate the magnetic properties in the Fe 100- x Me x ( Me = Al, Ga, Ge, 0 ≤ x ≤ 14 at. %) system, we used the Korringa–Kohn–Rostoker Green's function method implemented in the SPRKKR software package (a Spin Polarized Relativistic Korringa–Kohn–Rostoker code) [8]. The fully disordered structure A 2 was investigated in the work. For this phase, Fe and Me atoms are randomly distributed in the Wyckoff position 2 a (0, 0, 0). To create non-stoichiometric compositions, we used the single-site coherent potential approximation (CPA). The use of CPA allows us to construct an averaged potential for a lattice site occupied by several types of atoms [8]. Note that this approximation successfully describes the properties of many compositionally disordered (non-stoichiometric) alloys. The crystal lattice parameter in the calculations was varied in the range of 2,7 ≤ a ≤ 3,0 Å.

In the first stage, we performed calculations of the Heisenberg magnetic exchange constants J_i j in the formulation of A. Lichtenstein et al. [9]. The calculations included the use of the spin-polarized scalar-relativistic Dirac Hamiltonian with l _max = 3. To perform both self-consistent and J_i j calculations, 4 495 k -points were generated by a 57×57×57 k -grid. For the exchange-correlation potential, the generalized gradient approximation in the Perdew–Burke–Ernzerhof (PBE) formulation was used [10]. Obtained exchange coupling constants were used to estimate the Curie temperature T C in the mean field approximation [11]. J_i j parameters in Curie, temperature estimation were taken into account up to the 49th coordination sphere and were limited to a value multiple of 6 lattice parameters.

At the first stage, the magnetic exchange interaction parameters were calculated for the A 2 structure of the Fe 98 Ga 2 alloy with the experimental lattice value a 0 = 2,87 Å [12]. Fig. 1 shows the values of

Jij between Fe atoms depending on the distance between the atoms (in units of the crystal lattice parameter). The exchange interaction between pairs of Ga-Ga and Fe-Ga atoms does not exceed

0,1 meV and is excluded from consideration. In Fig. 1, J ij exhibit oscillating damped behavior. The largest FM interaction is observed in the first coordination sphere of Fe atoms and is ≈ 22 meV. Let us consider how the values of J ij change depending on the crystal lattice parameter and the concentration of Me = Al, Ga, and Ge atoms.

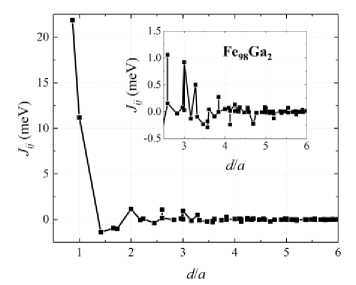
Fig. 1. Magnetic exchange interaction constants J ij as a function of the distance ( d / a ) between the pairs of i and j atoms, calculated for the experimental lattice value.

( a 0 = 2,87 Å) [11] in the A 2 structure of the Fe 98 Ga 2 alloy

Fig. 2 shows the distribution of the magnetic exchange interaction constants for the Fe_{100- x} Al _x alloy series depending on the value of the crystal lattice and the concentration of Al atoms for the first three coordination spheres (Fig. 2(a) – at a distance of 4 3 /2 a , Fig. 2(b) – at a distance of a , and Fig. 2(c) – at a distance of а/ 2 a ). The J_i j distribution has a non-linear behavior. Between the nearest Fe atoms (Fig. 2(a)), depending on the Al concentration, the change is no more than 5 meV, from ≈19 meV for pure Fe to ≈ 24 meV in the

In the second coordination sphere (at a distance of a , Fig. 2(b)) the distribution of exchange parameters is different, and two regions can be distinguished in the distribution depending on the lattice parameter. In the first region with small values of the lattice parameters ( a ≤ 2,82 Å), the J_i j parameters change slightly with increasing Al concentration, increasing almost linearly with an increase in the lattice parameter at a fixed Al concentration in the alloy. In this region, the parameter values change from ≈4,5 to ≈10,5 meV. The second region in Fig. 2(b) is characterized by a decrease in magnetic exchange with an increase in the Al concentration at constant values of a and a fixed Al concentration in the alloy. In this region, the change in the parameters of the magnetic exchange interaction is observed from ≈8,0 to ≈14,0 meV.

In the case of interaction between Fe atoms located at a distance of 4 2 (Fig. 2(c), the third coordination sphere), a region of antiferromagnetic interaction is observed in the distribution. This region is observed for lattice parameters of 2,8 ≤ a ≤ 3,0 Å and in the concentration range of 0 ≤ x ≤ 8 at. %. In general, a weak (no more than 4 meV) change in the constants of magnetic exchange interaction in the third coordination sphere can be noted.

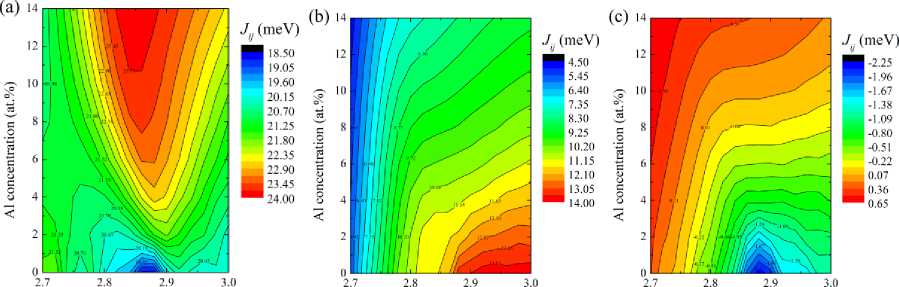
Lattice parameter (A)                              Lattice parameter (A)                             Lattice parameter (A)

Fig. 2. Distribution of the magnetic exchange interaction constant of Fe 100- x Al x alloys between Fe atoms depending on the crystal lattice parameter a and the Al concentration x in (a) the first, (b) second, and (c) third coordination spheres

In Fe-Ga and Fe-Ge alloys, the behavior of the magnetic exchange interaction constants is similar. The difference lies in the magnitude of the parameters associated with the presence of Me = Al, Ga, Ge atoms in the alloys, which was shown earlier in our works [5–7, 13–17].

In [5–7, 13–17], the authors showed that when modeling using the Monte Carlo method, the calculated Curie temperature values depend significantly on J_i j 's value. Taking this fact into account, in the present work, we analyzed the influence of the value of the crystal lattice parameter and the concentration of nonmagnetic atoms in the Fe 100- x Al x , Fe 100- x Ga x and Fe 100- x Ge x alloys on the Curie temperature. The values of T_С shown in Fig. 3 as a function of the crystal lattice parameter and the concentration of Me = Al, Ga, Ge atoms were obtained in the mean field approximation, which, as shown by the results of [4, 15], gives overestimated values compared to experimental values, but allows for a qualitative repetition of the experimentally observed trends [4, 18, 19].

Fig. 3 demonstrates that for all three systems: Fe-Al, Fe-Ga, and Fe-Ge, the T_C distributions are similar, and the main difference is observed in the range of lattice parameters from 2,9 to 3,0 Å. Up to lattice parameter values of a ≥ 2,94 Å, Curie temperatures have a maximum in the range of Me = Al, Ga, Ge atomic concentrations from 0 to 2 at. %. This behavior does not coincide with the observed experimental concentration dependence of the Curie temperature, according to which the behavior of the T C ( x ) curve has a descending behavior when Me = Al, Ga, Ge atoms are added to pure iron [12, 20–22]. Note that in the case of the Fe-Ge alloy, a concentration of ≈ 4,5 at.% can be distinguished, where the second maximum is observed at a = 2,9 Å.

Fig. 3 shows the T_C ( x ) cross-sections corresponding to the experimental values of the crystal lattice parameter [12, 20, 21] and the crystal lattice parameters obtained by ab initio geometric optimization of the crystal structure [6, 7, 23]. For visual clarity, Fig. 4 shows the Curie temperatures as functions of the concentrations of Me = Al, Ga, Ge atoms along the experimental and theoretical dependences of the lat-

Физика tice parameters estimated for all the alloys under consideration (Fig. 3). It can be seen that considering both the experimental and theoretical values of a0 when calculating the TC does not allow us to obtain a dependence corresponding to the experimental TC(x).

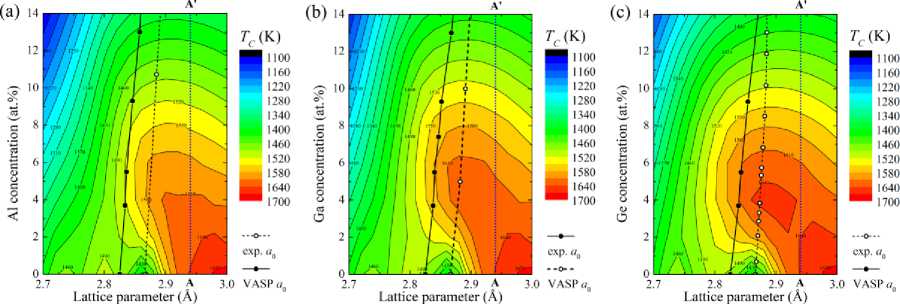
Fig. 3. Distribution of the Curie temperature for alloys: (a) Fe 100- x Al x , (b) Fe 100- x Ga x , and (c) Fe 100- x Ge x , depending on the crystal lattice parameter a and the Me = Al, Ga, Ge concentration x . Solid (open) circles are experimental (obtained from geometric optimization using the VASP software package) dependences of the crystal lattice parameters;

AA’ is the distribution cross-section

The figure shows that maximum Curie temperature corresponds to the concentration range of 4 ≤ x ≤ 8 at. %. The Curie temperature increases below this range and decreases above it. Nevertheless, such a cross-section (AA’) can be found in these distributions (Fig. 3), along which the Curie temperature dependence changes from higher to lower with increasing concentration of the alloying element and is qualitatively in agreement with the experimental dependence. This cross-section can be constructed for the parameter a ≥ 2,94 Å for all alloys. As can be seen from Fig. 4, for this value of the crystal lattice parameter, the Curie temperature decreases with increasing concentration of Me = Al, Ga, Ge.

The final thing to note from the analysis of the Curie temperature distribution is the absence of a direct correlation between the distribution of the largest interactions (between the nearest neighboring Fe atoms) and the distribution of the Curie temperature. From this, we conclude that the value of the Curie temperature is in a complex nonlinear dependence on the magnetic exchange interaction parameters.

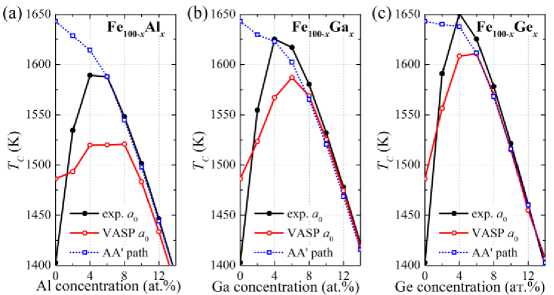
Fig. 4. Calculated Curie temperature values for alloys: (a) Fe 100- x Al x , (b) Fe 100- x Ga x , and (c) Fe 100- x Ge x , obtained with experimental, theoretical (by ab initio geometric optimization) parameters of the crystal lattice, and along the cross-section AA’ in Fig. 3 ( a = 2,94 Å)

Conclusion

In this work, for Fe_{100- x}Me_x alloys ( Me = Al, Ga, Ge, 0 ≤ x ≤ 14 at. %), the constants of magnetic exchange interaction J ij are calculated within the density functional theory and the Curie temperatures T C are estimated within the mean field approximation for the disordered phase A2 in the crystal lattice parameter range of 2,7 ≤ a ≤ 3,0 Å. The distribution of constants J_i j obtained in the work has a nonlinear behavior. The strongest interaction observed between the nearby Fe atoms is ferromagnetic and is ≈23 meV. In the second coordination sphere, the ferromagnetic interaction between Fe atoms is preserved and varies within 4–14 meV. In the third coordination sphere, antiferromagnetic exchange interaction is observed, which reaches a value of ≈ –2,5 meV. Estimation of the Curie temperature using the mean field approximation yields overestimated values compared to the experimental results. The Curie temperatures obtained with the experimental parameters of the crystal lattice have concentration dependences different from those observed experimentally, namely, they have a maximum Curie temperature in the concentration range of 4 ≤ x ≤ 8 at. %. On the obtained distributions of the Curie temperature depending on the lattice constant and the content of Me = Al, Ga, Ge in Fe 100– x Me x alloys, it is possible to obtain concentration dependences that qualitatively describe the decreasing behavior of T_C ( x ) ob-

Zagrebin M.A., Markovich I.A., Modeling of Magnetic Properties of Disordered BCC phase Kuznetsov A.S., Matyunina M.V., Butakov A.V. of Fe 100-x Me x Alloys (Me = Al, Ga, Ge) served experimentally. The study shows that the Curie temperature value is in a complex nonlinear dependence on both the crystal structure constant and the parameters of the magnetic exchange interaction.

This study was supported by the Russian Science Foundation, project no. 24-22-20086,