Conformal cyclic phantom energy dominated cosmological scenario from loop quantum cosmology

DOI:

Despite numerous success by general relativity on large scales, to understand the smaller structure of spacetime, a theory of quantum gravity is required. The loop quantum gravity is an attempt at non-perturbative and background independent formulation of general relativity.

The quantum gravity approaches are required to understand the initial conditions of the universe, where classical evolutions break down at the initial singularity. As the backward evolution of the current universe ends with inevitable classical singularity, there requires a meaningful quantum theory of cosmological evolution to understand the whole picture without violating the known laws of physics. The loop quantum evolution in terms of difference equations for a wave function permits the extension of quantum spacetime beyond the classical singularities. An updated review on loop quantum gravity can be found in [3].

During the evolution of the universe, any classical singularities are resolved and avoided, with the solutions provided loop quantum gravity formalism [4]. The loop quantum gravity formalism provides a model to understand the earlier stages of the universe. Some other attempts to resolve the classical singularities can be found in the literature [8; 10].

Expansion of the universe is defined by the Raychaudhuri equations. The Raychaudhuri equations also explain the curvature effects of the future singularities. At the quantum spacetime level, the formation of singularity is avoided by modified Raychaudhuri equations [6].

The phantom dominated final stages of the universe is predicted to extend its evolution conformally into the higher dimension is presented in [12]. The present work aims to understand the role of dark matter and dark energy interaction in the present universe with 3+1 dimensions.

The dynamics of K-essence and the effect of LQG in the earlier stages of the universe is studied and its consistency with the FRW equation is reported in [19].

The Raychaudhuri equations connect the rate of change of area with geodesic congruence, which has connections with shear and rotations of geodesic congruence. By analysing Raychaudhuri equations one can understand the avoidance of future singularities in some special cases as well.

The evolution of the universe is premiered by various cosmological models. In addition to success, every cosmological model has its limitations too. Among them, the big bang model stands high on the mountain. To resolve the flaws of the big bang model the conformal cyclic cosmological model introduces new paradigms [24]. With the implementation of such a model, the late time scenario of the universe is discussed in this work. On conformal cyclic cosmology, the Poincare-Einstein type of approach is discussed in [16]. The authors showed that the single spherical wave from the previous aeon in the new aeon split into three portions of radiation. To predict the existence of the conformal evolution of the universe, the circles in the cosmic microwave background is observed [15]. Those circles could be formed by the interaction between the last scattering surface and the gravitational waves emitted from the pre-big bang phase.

Fusing the phantom dominated quantum universe with the conformal cyclic universe scenario provides many surprising results. Datasets of masses of the black hole and starforming regions are discussed for the conformal evolution of the universe to understood the dark matted dominated evolution. Similarly for various values of equations of the state and the evolution of the scale factor is also reported.

Those datasets are visualized and reported with the availability IllustrisTNG data [14; 27]. With the help of IllustrisTNG data, large scale universe scenario and the gravo-magneto hydrodynamical solution within the universe are understood with simulations. These datasets have three various simulation sets, namely TNG10, TNG100 and TNG300. They indicate the rough cubic volumes of the stated magnitudes. The Illustris database has great advantages. Recently the Illustris simulation is used for estimation of the galaxy quenching rate [29].

From Illustris data sets galaxies with distant cores are analysed [7]. The kinematic behaviour of cores of the galaxies is reported.

Beyond the critical density the accelerated expansion is predicted as a consqeuence of cosmological cosntant.

In section 1 various rip off time is reported. In section 2 the role of phantom energy dominance and big rip is discussed. The conformal cyclic cosmology is embedded with phantom energy domination is also discussed. Section 3 elaborates the big rip resolution for the conformal cyclic evolution. The scale factor resolution is carried out for the final stages of the quantum universe. The present work attempts to connect the evolution cycles of the universe beyond both the big bang and big rip using conformal cyclic cosmology. To verify the paradigm, the dark energy dominance and the possible big rip is analysed with cosmological data sets. From the Illustrs datasets, the non-interaction of dark matter and dark energy is represented. And as a consequence of such a result, a possible future big rip avoidance is predicted.

1.    Dark energy dominance and big rip

Standard cosmology suggests that the universe without the presence of dark energy, in an expanding phase, its matter content will get liquified and its space gets expanded as the universe grows in size. The density of the universe approaches towards the lower levels. After a certain density is reached the universe stops its expansion too. Hence its expansion phase will be followed by a contraction phase. The critical density stated here is the least possible density of the universe. At the end of that contracting phase, the universe will end with a big crunch. Even though the cosmological constant is smaller than the expected value from quantum gravity, the term has been added in the Einstein field equations. When cosmological constant Л with the equation of state w = — 1 comes into play the scenario provides interesting results. The cosmological constant looks like a constant as the universe expands. Physicists don’t yet resolve the conflict between the theoretical and experimental values of the cosmological constant.

The cosmological constant (sometimes mimicked as dark energy) usually works against gravity. In addition to the cosmological constant there exist another variation of it in terms of lower values of the equation of state ( w <  — 1 ). Those energies are called phantom energy. Our universe consists of 4% Baryons 20% dark matter and remaining 76% as the form of dark energy. From standard cosmological model the accelleration equation is understood as

R 4 n C _o .

ъ = —^{( p} + ³ p ) . ⁽¹⁾ R 3

The sign of equation 1 determines the nature of the expansion of the universe. Dark energy is described as a cause for the accelerated expansion of the universe. In general, the dark energy emits no light and it has large negative pressure

P x ~ ^—p x - (2)

Understanding the behaviour of dark energy density can be a key to understand the final stages of the universe [25]. Eternal expansion takes place in the universe with flat and open models and they face future collapses. If the dark energy decayed with time, then, expansion of the flat universe would slow down. In the cosmological scales, in addition to dark energy, another version namely the phantom energy is also available [5].

On the other hand, the phantom energy has the equation of state parameter as w <  — 1 . The phantom energy let the galaxies be ripped off in the latter times of evolution. Without the presence of any dark energy, the universe will only be dominated by gravitational force, which will lead to a gravitational collapse. Within the limit — 1 <  w < — 3 the galaxies will remain in gravitational bound, despite of growth of the scale factor [23]. From the FRW equations, the dark energy dominance can be found as,

Н ² = ( "- У = // ■ " + (1 - П _т )а - 3⁽¹⁺ " ⁾ ]. (3) \ а/ а ³

For w <  — 1 the universe will accumulate more dark energy during the future evolution. By the dominance of phantom energy, the universe will be ripped off by diverging the scale factor within the time scales,

2                               -i trip — to ~ 3(1 + Ш) Н0 (1 - ^m) 2 '                       (4)

Here in equation 4, t ₀ is current time of the universe. With current values w = — 2 and Н 0 = 70Km/sec/M Pc, the big rip will approach at ~ 22 Gyr from now [11]. During the big rip planets with radius R which revolves around a host star of mass M will be ripped off, while the mass becomes

^M = ^— ”3”^{( p + 3p)R} 3 -

If the mass of the planet satisfies, — 4 ⁿ ( p + 3p)R 3 < M the planet will remain in the gravitational potential without any perturbations. The gravitational bounded system will be ripped off at the time

₊ V 2 | 1 + 3 ш | ^t ~ p             -

6 n (1 + ш )

That rip off time will be independent of Н 0 and О д . During the event of the big rip, the galactic clusters will be torn off before the end of the universe. In general, the Andromeda galaxy is predicted to collide with our galaxy Milky Way. But 35 Gyr before the big rip, the Andromeda galaxy will be ripped off. Hence the collision between Andromeda and Milkyway will be avoided. Within a million years before the big rip, the local galaxies will be ripped off. Just months before the big rip atoms and nuclei will be ripped apart. The final stages of the universe will remain as plasma. The physical universe will not face the big rip as the matter content will be completely ripped off just before the big rip.

The non-interactions between dark matter and dark energy in the late time universe may consequence the avoidance of future big rip even in the presence of dark energy [13]. As an aeon avoid the big rip singularity, it continues towards the beginning of consecutive aeon. (Every cycle of the conformal cyclic cosmological model is reprecented as aeon [17]) The dark matter in the high energy scales may provide the possible consequence of graceful exit to the future aeon. To understand the non-interaction between dark matter and dark energy, analysis of large scale dark matter is required.

The ratio between black hole mass to the dark matter content of the universe in large scales are obtained from the IllustrisTNG data [28], with dark matter function

m

M am

M tot ¹

where M _dm is mass of dark matter and M _tot is total mass. f _am is measured in the entire subhalo. The large scale dark matter provides a glimpse of its density and invariance in expansion. This indirectly predicts the avoidance of future big rip. Some behaviour of dark matter in large scales from IllustrisTNG data sets are reported in the discussion section of the current work. The ideas defined in the above sections are implemented in the conformal cyclic model in the next section.

2.    Phantom dominance and conformal evolution

To calculate the evolution of the phantom dominated quantum universe the modified Raychaudhuri equation from loop quantum cosmology is implemented. It is written as [21]

a    4 n Gp (    4p\         /    2p\

— —---— I 1 —--- I — 4 n GP I 1 —--- I .                  (8)

^{a         3}    \      ^p crit /             \      ^p crit /

As the equation of state connects pressure and density as (w — ^ ) , then the equation 8 is modified as

a

a

⁴-П^( A — JL) +3w (1 — -^W

• ³    \ \ ^p crit /         \      ^p crit / /

For the values, w < — 1 the universe will be dominated with phantom energy and behave violently. For the case phantom dominated evolution, the equation of state is set to w — -38, hence the equation 8 becomes a   4nGp /    20p

^{a       3}    \      ^p crit

Note the positivity of the equation 10, which turns to be a repulsive solution against the gravitational collapse of the universe. Hence the universe undergoes an accelerated expansion. Also, the universe will be repelled more rapidly and violently than dark energy can do. Further negative values of the equation of states the quantum universe behave exponential expansion scenario. But the quantum tensions will not allow the ever-expanding scenario. As the energy density approaches the critical densities which are obtained by loop quantum predictions ( p ~ p _crit with p _cr i _t ~ 0.41 p _p/ ), the universe would behave with a different perspective. The expanding scenario will stop at the densities near the critical density. Hence the sign changes as

- — 36 n G p c„t . (11) a

The positivity in sign in equation 11 means, the existence of rapid expansion solutions beyond the bounce in the the conformal evolution. Hence the universe will start to expand rapidly soon after the bounce. It also confirms the consmological constant dominance over the inflation scenario in conformal cyclic evoution.

The phantom dominated divergence of the universe is set to have maximum limits. The values of the modified Raychaudhuri equation claims to have in the order of numerators of the equation of state. As the values of the equation of state lowest possible values, the universe bounces off rapidly while the energy density approaches the critical values. Further expansion in new aeon will be at a greater rate than the previous big bang kind of expansion. Due to the transition from Raychaudhuri solutions, it has been confirmed that the conformal evolution will not end by facing the big rip. Rather the evolution will continue beyond the big rip.

From the phantom evolution beyond the singularity, one can obtain the conformal mapping between two aeons. The 2 surfaces between two successive aeons are obtained by the quantum gravitational effects offered by the phantom dominance from the previous aeon.

An aeon topologically exits into future aeon by crossing the big rip singularity (see fig. 1). As every possible singular universe conformally expands into future aeons, the phantom dominated big rip quantum universe without facing an ever-expanding scenario. The presence of phantom dominance let the fiducial cells to be dominated with cosmological constant over the inflaton potential, and let them to expand rapidly. In a conformal phantom dominated universe the final stages of the aeon must come across the big rip singularity for the conformal evolution. To do so, a big rip resolution has to be done.

TOPOLOGICAL MAPPING BETWEEN AEONS

CURRENT UNIVERSE

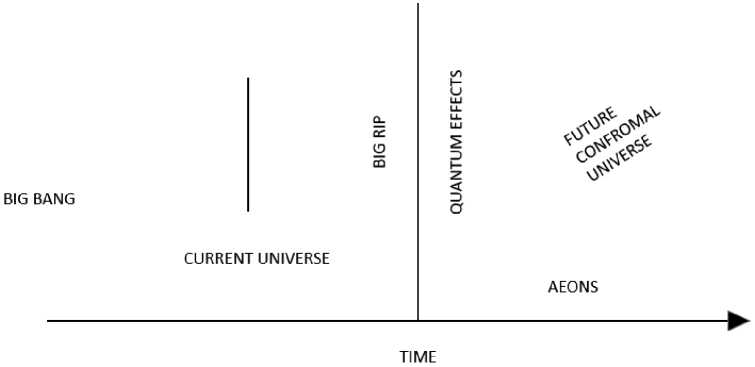
Fig. 1. Evolution of Aeons beyond big rip singularity

3.    Big rip resolution

The big rip is caused by the phantom energy. The scale factor of the universe is filled with phantom energy is written as [1]

- 2

a(t) = a * (t — t b-r ) ^3(|ш|-1) .                                         (12)

Here a * is the integration constant, which is expressed as

a *

= ^a 0

- 3C ( | w | — 1) • 2

- 2

3(H - 1)

and

,- (-T) 1,                            „4, к = 8nG.                                 (15)

The big rip occurs when the time approaches

- 2

^th' ^{- t o} + 30( | w | - 1) > °'

To avoid the future big rip the scale factor resolution should be considered. To do so the scale factor is replaced with a modified version of it which is obtained from our previous result as [20]

°- ( I ^{p c} t ² ) ³ [ i+^tan 2 [ (| ^p = t 2 +1) ³ ] 2 m 2 (t - 1^ ) 2 ] •               (17)

Hence the universe can avoid the future big rip with the values of the scale factor obtained from equation 17. From equation 16 the value of the time to rip off is obtained as

^{(t — t} br ^{) 2}

6 n G( | w | — 1) 2

Equation 18 is placed in equation 17 and the modified scale factor for the big rip avoidance is found as

-(I--)'

^1+tan 2 [⁽| ^{P c t} 2 ^{+ 1)} 3] 2^ 2 2 n G(\w\ - 1) 2 ] •

The bounce occurs with this scale factor and conformal continuation of the aeon is found plausible. The universe beyond the big rip resolution acts like disconnected quantum regions. Hence it resembles the Planck scale singularity.

As like equation 9 the equation of state w — - 38 is implememnted in equation 19.

° ^- ( I ^{P c t} 2 ) ³ [ 1^{+ tan} 2 [ ⁽4 ^{P c t} 2 ^{+11 1} ] wO n Gs i ] •               ⁽²⁰⁾

The bouncing scale factor from equation 20 is introduced with the Ekpyrotic universe scenareo [22]. The bouncing poterntial is calculated as V q — ° . Hence the equation 20 is modified as

°    ^| P cri^     •

At a very later time from the big bang, the universe approaches the time in larger magnitudes. The big rip will occur at ~ 35Gyr [5]. Hence the bouncing scale factor becomes very large for the post big rip conformal evolution of the universe. But such a universe will extend into another brane as suggested by the Ekpyrotic universe and conformal cyclic scenario.

As the density of phantom energy reaches the Planck scales the expansion will be at a maximal rate. At this level, the universe behaves as quantum patched island universes. As far as concerned the event horizon of the island universe will shrink as the phantom effect dominates. Hence the event horizon of the universe will also shrink to patch sized discrete universes. Then the comoving radius of the universe will be in the Planck scales

R - AZ p . (22)

The phantom dominated quantum universe behaves as discrete Planck scaled quantum patches at its later stages. That singularity can be mapped to the initial singularity of the next aeon. Even beyond the density increases, the phantom potential will behave as gravitational potential, and the universe will continue its evolution as per the standard cosmology. Hence it is observed as, the phantom energy behaves like ф _р нап ^ Ф е// while ^p ^ P crit -

As the quantum effects dominate each quantum universe the quantum cosmology scenario can be applied to every fiducial cell of the island universes. As the cosmological horizon shrinks the flatness of the individual fiducial cell disappears and the quantum curvature starts to emerge.

4.    Discussion

As the phantom energy density reaches the scales of critical energy density, the modified Raychaudhuri equation changes its sign which is conformed in equation 11. The classically impossible evolution beyond the big rip is made plausible by loop quantum corrections on conformal cyclic cosmology. The quantum bounce beyond the big rip is obtained in equation 19. At the time of the big rip, the quantum scale factor let the evolution behave gravitationally and let the future conformal evolution will be kicked off. The cosmological constant and expansion of the universe in quantum gravitational aspects are discussed in the equation earlier.

The big rip bound quantum universe may tunnel into future aeon as like quantum tunnelling universe [26]. The formation of a future aeon will be initiated once the universe bypasses the singularity.

Various datasets on various confrontations of the calculated and the results are analyzed. For the case of phantom energy w <  — 1 the violent scenario on the cosmological parameters are understood by studying its effects on scale factors and density parameters. For w = — 2.66 and w = — 10 the scale factor to density ratios are predicted in the figure 3.

At various values of w , the ratio between the relative density to the scale factor comes to unity. As w = — 10 , the curve seems to be flat after 0.9 p _crj_t . Unlike the gradual increment of scale factor over w has lesser values than w = — 10 , the increment of the rapid scale factor is found.

The lensing power spectrum [9] for various phantom energy scenareo are analyzed and plotted. The plot is obtained form L vs L y values. With L y = [L(L + 1)] 2 С ^фф /2 п .

For various equation of states from w = — 1.9 to w = — 0.6 the lensing power spectrum is reported in figure 5 The slope shows the gradual approach towards the maximum, by the values between 10 to 10 2 for L values. The curve shows distinguished lines.

A black hole in the conformal universe is considered as the seeds that form the existence of the dark matter in the next aeon. Such black hole remnants from previous aeons are called erebons [18]. In the phantom dominated conformal evolution, the role of future erebons can be discussed with dark matter-dominated black hole datasets from TNG300. In the expanding universe, the formation of the stars looks the as far history of future aeons. From the EiBI model, it is also understood that the interaction between dark energy and dark matter would contribute to the avoidance of big rip scenario [13]. To study star formation in the dark energy dominated large-scaled universe is reported in figure 4.

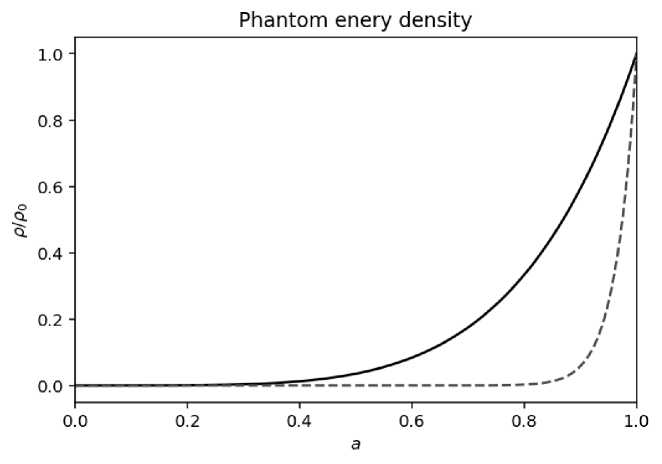
Fig. 2. Effect of equation of state on the densty parameters of the expanding universe for го = - 2 . 66 and го = - 10 is shown. Here го = - 10 is shown as dashed curve

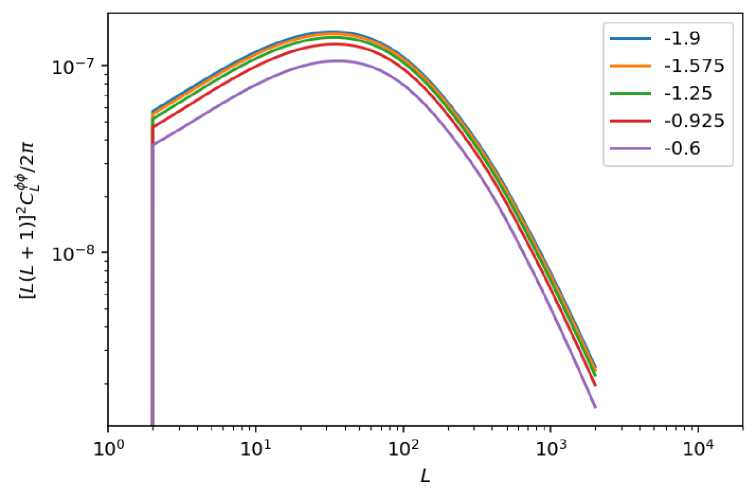
Fig. 3. Lensing power spectrum for various equation of states

In image 4 the mass of the black hole and star formation rates are plotted. The star formation with a higher number of galaxies can be found in the mid-horizontal best-fit regions. The formation rate varies from — 1 to 2 and beyond. In the X axis for the core black hole masses from 6[log (M ₀ )] , is taken for the plot. Around the black hole, mass ranges 6.25[log(M ₀ )] the formation rate seems discrete. After 6.4[log (M ₀ )] the star formation rate

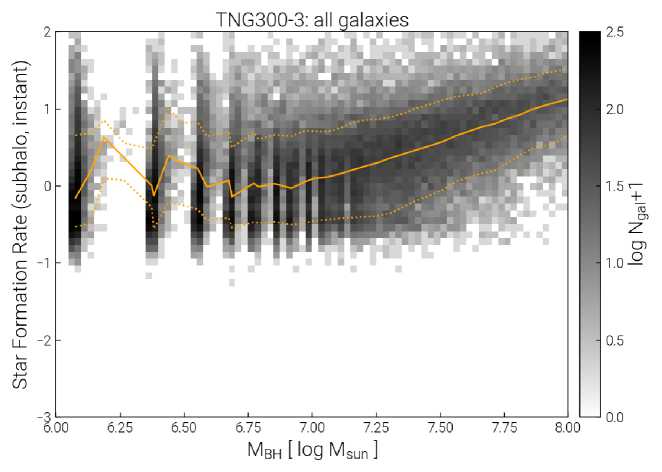
Fig. 4. Star forming rate in large scale universe with the consequence of dark matter is shown in the figure increases gradually. After 6.75[log (M0)] the concentrative star formation rates look denser. The number of galaxies also look high. More star formation regions are concentrated on the galaxies with black hole masses greater than 6.75[log (M0)]. From the basis of the same data, the concentration of supermassive black holes in the galaxies can be predicted. It is also understood that the future aeon might exhibit the Hawking points as predicted in [2], which could be a consequence of SMBH remnants of the previous aeon. The dark matter mass function is related to the mass of black holes (from equation 7) in a large scale structure is reported in figure 5.

Figure 5 provides the data that includes the black hole masses of the galaxies and densities of galaxies. The best fit of this data seems flat and evolves unperturbed throughout the spread. Initially around 6.1[log (M ₀ )] there exist a spike in the dark matter mass function. But the concentration of galaxies exists within the best fit data with / _DM ~ 0.9 . Between 6.2[log (M ₀ )]&6.4[log (M ₀ )] there exist a gab among the densities of galaxies. Further increment of black hole masses shows the increment of galactic densities with / _DM values 0.8 to 1.0 . In the same plot some concentration of galaxies exist between the / _DM values 0.2 to 0.4 . Similarly some galaxies exist in / _DM values of 1.0 . Apart from the extrema, the data fits immersively within / _DM values 0.7 to 0.9 . The dark matter mass function and density of galaxies will be perturbed by the presence of phantom energy and the interaction between dark matter and dark energy. This perturbation leads the classical universe to conformally exit into the cyclic universe.

The quantum gravitational results conform that, the universe approaches non zero minimum volume which is predicted by the loop quantum cosmology. It is analyzed that, the classical universe will not be completely ripped off at the phantom final stages. From the plots, one can understand that the phantom dominated universe, will leap towards future conformal evolution cycles of the universe, as the consequence of the increment of phantom energy density. Thus the universe will not stop its evolution by approaching the big rip.

Similarly one can find that the universe might have evolved from the non-singular bounce. The evolution will extend to future cycles of the cyclic cosmological scenarios. It has been predicted that the perturbation of dark matter mass function and densities of galaxies by the presence of dark energy in the large scales using Illustris data. As a result, the conformal evolution of the universe avoidance of the big rip and loop quantum cosmological solutions are discussed to exist. This result can be considered as a support for the validation of conformal cyclic cosmology.

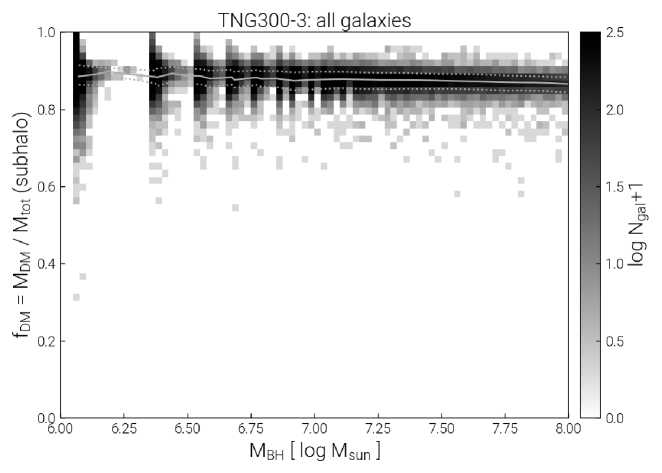
Fig. 5. Mass function and Black hole variation is shown in the figure

Conclusion

From the obtained results one could understand the possible existence of a conformal cyclic cosmological model with the presence of phantom energy and with the backend support of loop quantum cosmological model. Its also known that the quantum cosmological evolution in the phantom dominated final stages of the universe can extend even beyond the big rip singularity. The quantum structure of spacetime and its consequence on quantum cosmology led the conformal cyclic evolution to be consistent in all possible cosmological model. Large scale bounce is predicted in equation 21 suggested the conformal evolution and Ekpyrotic scenario.

With the presence of various simulations, the scale factor’s evolution concerning the increment of phantom energy can be understood from the current work. Even though the scale factor, energy density and pressure diverges during the big rip, there exists a possibility to trigger the quantum evolution of the future conformal universe. In general, the big rip singularity is predicted as, the singularity which cannot be avoided by the universe in its future. Also, it is considered as an endpoint of the evolution of the universe. But the calculations presented here confirm the avoidance of future big rip singularity, using loop quantum cosmological formalism. It is also suggested that the initial stages of the universe might consist of unaltered quantum cosmological theories.

Its also understood that the phantom energy could be in the dominant form in the transition phase of the conformal evolution of the universe. The current universe copes with a positive cosmological constant (DeSitter universe). If the cosmological constant tends to have negative values after the quantum bounce, the universe may behave like AdS like the universe. Hence the solutions presented here, it is derived that the bounce scenario from phantom dominated solutions could initiate AdS like quantum universe scenario. It is because of the bouncing nature of the universe with the presence of phantom energy which changes its sign from positive to negative.

The changes in sign of the accelerated expansion act like a critical point, beyond that the universe faces deceleration.

By resolving singularities via quantum mechanical treatment, the big rip singularity will also lose its strength. The big rip singularity is a strong singularity from where the space-time evolution can not be extended further. But the big rip singularity is resolved into the week (typeII) singularity by loop quantum gravity. Hence the conformal cyclic evolution of the universe will be extended to the next aeon.