Conservativity Principle Violations for Ontology Alignment: Survey and Trends

Published Online July 2016 in MECS

The alignment between ontologies is a crucial task in many application domains [3]. As not exhaustively, we can cite: Semantic web, communication in MAS (MultiAgent System), data warehouse, integrating schema/ontologies, etc. Ontology is defined as the conceptualization of objects recognized as existing in a domain, with their properties and linking relationships. The problem is that given the same domain or related domains, it is possible that several ontologies are available (developed simultaneously by several different communities). The comparison of two ontologies, passing the one to the other or integrating them becomes therefore necessary.

This necessity does not make alignment faultless and impeccable, since mappings can lead to many undesirable logical consequences in the aligned ontologies and therefore the domain covered by these ontologies. In [13] three principles were proposed to minimize the number of potentially unintended consequences, namely: (i) consistency principle, the mappings should not lead to unsatisfiable classes in the integrated ontology, (ii) locality principle, the mappings should link entities that have similar neighborhoods, (iii) conservativity principle, the mappings should not introduce new semantic relationships between concepts from one of the input ontologies. These principles have been actively investigated in the last years (e.g., [18], [25], [10], [13], [12], [17], [21]). The conservativity principle has been identified for instance in [13] as an alignment which allows the interaction between ontologies, rather than providing a new description of the domain. However, [23] proposes a different variant of the conservativity principle where the integrated ontology Ou must not introduce new subsumption relationships between concepts within the input ontologies.

In this paper we focus on the conservativity principle for ontology alignment. Actually, we achieved a thorough survey and make the following contributions:

• •    We formally define and illustrate the conservativity principle problem, highlighting the complexity of the problem. We modify and adapt an example presented in [23] which is a use case based on the Optique’s¹ application domain.

• •    We systematically review the literature on the conservativity principle problem, offering a complete state-of-the-art by presenting, comparing and discussing the existing approaches.

• •    We analyze lacks of existing approaches, discussing general open issues which make difficult to deal with conservativity principle violations. This allows us to underscore open research challenges.

We structure the remainder of this paper as follows: Section 2 summarizes the basics concepts and definitions we will rely on along the paper. In Section 3, we introduce our problematic after analyzing some definitions mentioned in literature. This section is also an examination of the conservativity principle problem studied in several related works. Section 4 is a comparison of different surveys performed about alignment maintenance on basis of the studied subproblems. Section 5 present some statistics presents on one side revealing the importance of this field and the other side a numerical comparison between approaches and surveys studied here. Finally, Section 6 discusses our findings and challenges of different nature, representing open research issues and wraps up with concluding remarks and outlines future work.

• II.    Preliminaries and Notations

In this section, we define the edges of the conservativity principle problem. So we define some important notions for our work.

The concept of Ontology can be seen as a logical theory [14]. So it is a pair ( S , A ), where S is the signature describing the vocabulary, and A is a set of axioms specifying the intended interpretation of the vocabulary in a domain of discourse. The signature is the set S = C U P U I . C represents the vocabulary to designate concepts. P is the vocabulary to designate properties and I is the vocabulary to designate individuals. We distinguish between the origins axioms A and their logical consequences A^* (also called closure). Theory ( S , A ) is called the presentation of ( S , A^* ). In this work, we limit ourselves only to S = C U P and we designate by ontological entity a concept or a property.

Ontology alignment is the task to detect links between elements from two ontologies. These links are referred as correspondences and express semantic relations. According to Euzenat and Shvaiko [6] we define a correspondence as follows and introduce an alignment as set of correspondences.

Definition 1 (Correspondence and Alignment). Given two ontologies O₁ and O₂ , let Q a function that defines sets of matchable elements Q ( O₁ ) and Q ( O₂ ). A correspondence between O 1 and O 2 is a 5-tuple ( id , e 1 , e2 , r , n ) such that, id a unique identifier, e 1 e Q ( O 1 ), e₂ e Q ( O₂ ), r is a semantic relation, and n e [0; 1] is a confidence value. An alignment M between O 1 and O 2 is a set of correspondences between O₁ and O₂ . We restrict r to be one of the semantic relations from the set {c, 2, =, ⊥ }

In order to reason about alignment, two classes of approaches have been introduced. The first class is based on model theory. IDDL [29] and DDL [2] are two examples of approaches of this class. Based on an axiomatic approach, the second class called reductionist semantics [16] is to interpret correspondences of the alignment as axioms in some merged ontology. In this paper, we use an example of this semantic called natural semantic. It involves building a merged ontology through the union of the two ontologies to align, and axioms obtained by translating relations of the alignment. We introduce this semantic through its merged ontology.

Definition 2 (Merged Ontology). Given an alignment M between two ontologies O 1 and O 2 and trans: M → A a function that transforms a correspondence to an axiom. The merged ontology is defined by O 1 U M O 2 = O 1 U O 2 U trans ( M ).

After defining the most important notions for the conservativity principle problem, we illustrate the problem itself.

• III.    Analysis and Examination

In order to analyze the conservativity problem through all its sides, we discuss in the present part of the paper the problem statement which will allow us to: first, defining the principle, and thereafter, comparing our definition against others approaches in the literature.

• A. Problem Statement

This section is organized according to the following points: example of motivation, problem definition and comparison with other definitions mentioned in the literature.

• 1)    Motivating example

Table 1 shows the fragments of two ontologies in the context of the Oil and Gas industry. The ontology O₁ has been directly bootstrapped from a relational database in Optique, and it is linked to the data via direct ontology-to-database mappings. The ontology O 2 , instead, is a domain ontology, based on the NPD FactPages, preferred by Optique end-users to feed the visual query formulation interface².

The integration via ontology matching of O₁ and O₂ is required since the vocabulary in O₂ is used to formulate queries, but only the vocabulary of O₁ is connected to the database. Consider the set of mappings M in Table 2 between O 1 and O 2 generated by an off-the-shelf ontology alignment system. As described in Section 2, mappings are represented as 5-tuples; for example the mapping m 1 suggests an equivalence relationship between the entities O₁ :Well and O₂ :Well, with confidence 0.9.

• 2)    Problem definition

In this paper we propose a general definition of the conservativity of alignment, covering any violations of the principle for which the alignment must not introduce any new entailments to the input ontologies.

Definition 3 (Conservatif Alignment). An alignment A between two ontologies O₁ and O₂ is conservatif iff ( O₁ U A O 2 ) 1= 5 ^ 3 i e { 1 , 2 }/ O i 1= 5 v 5 e A , i.e. any reasoning on the set { O 1 ∪ A O 2 } that leads to logical consequences δ must not surpassed the set of entailments generated by reasoning on { O 1 , O 2 } separately.

The reasoning on the set {O1 ∪ A O2} however, violates the conservativity principle, according to our definition of conservativity of alignment (Definition 3), and introduces new entailments (see Table 3) to the input ontologies O1 and O2.

Table 1. Fragments of the ontologies used in Optique

Ontology O 1	Ontology O 2
α 1 WellBore ⊆ ∃belongsTo.Well α 2 WellBore ⊆ ∃hasOperator.Operator α 3 WellBore ⊆ ∃locatedIn.Field α 4 AppraisalWellBore ⊆ WellBore α 5 ExplorationWellBore ⊆ WellBore α 6 Operator ⊆ Owner α 7 Operator ⊆ Company α 8 Field ⊆ ∃hasOperator.Company α 9 Field ⊆ ∃hasOwner.Owner	β 1 Exploration_well ⊆ Well β 2 Explorborehole ⊆ Borehole β 3 Appraisal_exp borehole ⊆ Explor_borehole β 4 Appraisal_well ⊆ Well β 5 Field ⊆ ∃hasFieldOperator.Field_operator β 6 Field_operator ∩ Owner ⊆ Field_owner β 7 Company ⊆ Field_operator β 8 Field_owner ⊆ Owner β 9 Borehole ⊆ Continuant ∪ Occurrent

Table 2. Ontology mappings for the vocabulary in O1 and O2

Alignment A
id	e 1	e 2	n	ρ
m 1	O 1 :Well	O 2 :Well	0.9	≡
m 2	O 1 :WellBore	O 2 :Borehole	0.7	≡
m 3	O 1 :ExplorationWellBore	O 2 :Exploration_well	0.6	⊆
m 4	O 1 :ExplorationWellBore	O 2 :Explor_borehole	0.8	≡
m 5	O 1 :AppraisalWellBore	O 2 :Appraisal_exp_borehole	0.7	≡
m 6	O 1 :Field	O 2 :Field	0.9	≡
m 7	O 1 :Operator	O 2 :Field_operator	0.7	⊇
m 8	O 1 :Company	O 2 :Company	0.9	≡
m 9	O 1 :hasOperator	O 2 :hasFieldOperator	0.6	≡
m 10	O 1 :Owner	O 2 :Owner	0.9	≡

Table 3. Example of conservativity principle violations

σ	Entailment:	follows from:	Violation?
σ 1	O 2 :Exploror_behole⊆ O 2 :Exploration_well	m 3 , m 4	YES
σ 2	O 1 :AppraisalWellBore ⊆ O 1 :ExplorationWellBore	β 3 , m 4 , m 5	YES
σ 3	O 2 :Field_operator ⊆ O 2 :Field_owner	α 6 , β 6 , m 7 , m 10	YES
σ 4	O 1 :Company ≡ O 1 :Operator	α 7 , β 7 , m 7 , m 8	YES
σ 5	O 1 :Company ⊆ O 1 :Owner	σ 4 , α 6	YES
σ 6	O 2 :Company ⊆ O 2 :Field_owner	σ 3 , σ 5	YES
σ 7	O 2 :Well ⊆ O 2 :Owner	m 1 , m 10 , α 10	YES

We have shown that the alignment violating the conservativity principle leads to non-desired entailments to the input ontologies. Therefore, a comparison between the different works on the conservativity principle can be considered as very important.

• 3)    Comparison of definitions

In order to position our definition of conservativity principle problem, we present in this part of the paper a comparison between several definitions provided in the literature. Since the Satisfiability preservation and Ontology change preservation are two instances of conservativity problem, this comparison is a classification of approaches in three dimensions: i. Approaches defining the Satisfiability preservation problem, ii.

Approaches defining the Ontology change preservation problem and iii. Approaches defining the Conservativity problem.

• i.    Satisfiability preservation problem

The satisfiability preservation of the alignment between ontologies was the subject of study in several works ([27], [25], [17] and [12]). In [27] the authors of Lily address the problem of debugging ontology mappings to improve the quality of mapping result. They define two types of inconsistencies:

• •    Mappings that form a circle: such type of unsatisfiability means that the mapping should not destroy the hierarchy structure ( is-a structure) in the ontology, for example: let’s take ( e ₁, e ′₁) ϵ ontology O₁ , ( e ₂) ϵ ontology O₂ . The following mappings form a circle leading to alignment inconsistency: m 1 : e 1 ⊆ e ′ 1 and m 2 : e ′ 1 ⊆ e 2 and m 3 : e 1 ≡ e 2 . Here, the equivalent mapping is treated as bidirectional is-a relation. The is-a circle destroys the hierarchy of ontology O₁ .

• •    Mappings that do not meet the equivalentClass/disjointWith axioms: in such case, alignment between ontologies should not introduce equivalences between disjoint elements in the inputs ontologies, for example: let’s take ( e 1 ) ϵ ontology O 1 , ( e 2 , e ′ 2 ) ϵ ontology O 2 . The

following mappings lead to alignment inconsistency: m1: e2 ⊥ e′2 and m2: e1 ≡ e2 and m3: e1 ≡ e′2. Here, the behavior of the alignment is inconsistent since it leads to two contradictory mappings m1: e2 ⊥ e′2 and ™1: e2 -L e 2 and m4: e2 ≡ e′2.

Stuckenschmidt et al. [25] proposed a theory for reasoning about ontology mappings. This work identified four properties that reflect the quality of a mapping, namely containment , minimality , consistency and embedding . The consistency principle claims that a mapping is consistent if it does not make a satisfiable concept in the target terminology unsatisfiable.

Meilicke [17] identifies the (in) coherence of ontology as: an ontology is called incoherent when there exists an unsatisfiable named concept or property; otherwise the ontology is called coherent. A concept C is defined to be unsatisfiable iff each model I of O maps C to the empty set, i.e., an instance of C cannot exist for logical reasons. Thus, a named concept or property C #i with i = { 1 , 2 } is unsatisfiable due to A with respect to O 1 and O 2 iff C #i is satisfiable in O i and unsatisfiable in A . the definition which interests us is the alignment incoherence definition: Given an alignment A between ontologies O₁ and O₂ with signatures S₁ and S₂ respectively, A is incoherent with respect to O₁ and O₂ iff there exists C _#i ∊ S _i with i = { 1 , 2 } that is unsatisfiable due to A with respect to O 1 and O 2 . Otherwise, A is coherent with respect to O 1 and O 2 .

LogMap [12] introduces the notion of Logical inconsistencies. Indeed, the ontology O₁ ∪ O₂ ∪ M resulting from the integration of O 1 and O 2 via mappings M may entail axioms that don't follow from O 1 , O 2 or M alone.

• ii.    Ontology change preservation problem

• [28]    defines the notion of conserving the changed meaning to refer the control of the propagation of knowledge from one version to another which is one of the known activity of alignment. If this propagation is not controlled, it can affect the meaning of ontological elements. An alignment M between two versions O 1 and O₂ conserves the changed meaning iff M verifies the following two properties:

∀ δ ∊ A ⁻, ( O 1 ∪ M O 2 ) ⊭ M (δ)

∀ δ ∊ A ⁺, ( O 1 ∪ M O 2 ) ⊭ M ⁻ (δ)

Such as: A ⁻ is the set of deleted axioms. A ⁺ is the set of added axioms and M ⁻ is the set of deleted mappings between two versions of the same ontology.

• iii.    Conservativity problem

In this section we explore various definitions of the conservativity problem of alignment between ontologies, for instance, in [13] an interesting definition of the conservativity principle was proposed. This definition required that, given an ontology source (say, O1) and the mappings M, the union (O1 ∪ M) should not introduce new semantic relationships between entities from O1. This definition takes only the ontology source and the alignment and don’t take the target ontology in consideration. However, this can be a subject of many neglected logical consequences when discarding the target ontology. Indeed, the following example presents a concrete case.

Another definition of conservativity principle [23] is given based on the definition cited in [13]. In this work the authors propose a different variant of the conservativity principle where they require that the integrated ontology O_u (i.e., O_u = O₁ ∪ O₂ ∪ M ) does not introduce new subsumption relationships between concepts from one of the input ontologies, unless they were already involved in a subsumption relationship or they shared a common descendant. As it is clear, this definition deals with conservativity principle violations only at the concept hierarchy level within the input ontologies, thereby it is also considered as incomplete to cover all types of conservativity principle violations.

To achieve our survey about different works on the conservativity principle, we present in the following (Table 4) a comparative table between several works according to their problem definitions.

Table 4. Comparison between approaches according to their problem definitions

Approach	Satisfiability preservation	Ontology change preservation	Conservativity
[27]	+	-	-
[17]	+	-	-
[10]	+	-	-
[12]	+	-	-
[28]	+	+	-
[13]	+	+	+ (*)
[23]	+	-	+ (*)
Our definition	+	+	+

(*): Here, the conservativity of alignment between ontologies is an incomplete process for reasons already discussed in the last section ( iii. Conservativity problem ).

We have shown that most systems ([27], [17], [10] and [12]) deal only with the satisfiability preservation problem. However, [28] addresses a more complicated problem: Ontology change preservation, which needs more sophisticated violations detection processes. the rest of the compared systems here ([13] and [23]) solve the conservativity problem with different degrees, since that [23] deals with conservativity principle violations at only the concept hierarchy level within the input ontologies, and therefore it cannot covers all types of violations even those concerning ontology change preservation. Whereas, [13] deals with the conservativity problem in a partial manner as discussed in the last section (iii. Conservativity problem). Our definition (III.A.2 Problem definition) is more general, covering any violations of the conservativity principle for which the alignment must not introduce any new entailments to the input ontologies. After this comparison, the analysis of the violations detection processes adopted by the mentioned systems arises as an important task to ensure a complete survey.

• B.    Conservativity violation detection

The present section highlights violation detection by analyzing at first approaches that address the general problem ( conservativity principle ) then, its instances ( ontology change and satisfiability preservation ).

Violations detection of conservativity principle was subject of study in [23] and [13]. As mentioned in the section above ( iii. Conservativity problem ), [13] states that the conservativity principle is based on the purpose of M , which is to enable the interaction between O₁ and O₂ , rather than to provide a new description of the domain. Indeed, the authors use a specific pattern to detect conservativity principle violations; this pattern is based on the following observation:

The OWL2 alignment M that encodes the contents of UMLS-Meta ³ contains only axioms of the form EquivalentClasses ( e₁ e₂ ) where e₁ is mentioned only in O₁ and e₂ is mentioned only in O₂ (note that different ontology sources use different namespaces to refer to their entities). This observation is used be to significantly simplify the problem in the following way: O 1 violates conservativity iff there exist axioms EquivalentClasses ( e 1 e 2 ) and EquivalentClasses ( e′ 1 e 2 ) in M , with e 1 and e′ 1 different entities in O 1 , such that O 1 alone does not imply the axiom EquivalentClasses ( e′₁ e₂ ). If this is the case, then the mappings EquivalentClasses ( e₁ e₂ ) and EquivalentClasses ( e′₁ e₂ ) from M are in conflict and one of them may be incorrect.

In order to identify such conflicting mappings, it suffices to (syntactically) check in M whether two entities from one of the sources are mapped to the same entity in the other source, and then check (semantically) whether these two entities were already equivalent with respect (only) to the former source. These checks can be performed efficiently in practice: the former is syntactic, and the latter involves a single semantic test using an ontology reasoner.

Section (iii. Conservativity problem) also indicates another variant of the conservativity principle cited in [23], where the integrated ontology Ou must not introduce new subsumption relationships between concepts within the input ontologies. This variant of the conservativity principle follows the assumption of disjointness proposed in [22]. So if two atomic concepts A, B from one of the input ontologies are not involved in a subsumption relationship nor share a common subconcept (excluding ⊥ ), they can be considered as disjoint. Hence, the problem of detecting and solving conservativity principle violations, is reduced to a mapping (incoherence) repair problem, if the input ontologies are extended with sufficient disjointness axioms. The detection of conservativity principle violations is done in the same way as LogMap (examined below).

For detecting ontology change preservation violation, [28] considers that initial alignment cannot be coherent. Because, some correspondences propagate axioms from one ontology version to another; this violates the constraint of conserving the changed meaning . The goal is to identify these correspondences and provide means to choose among them which must be eliminated. The identification of these correspondences is simply obtained by identifying the signature of the propagated axiom. To choose among correspondences, the author introduces an order relation called relevance relation on the signature elements of the propagated axiom. The relevance relation (noted < _rel ) compares the degrees of intentional persistence of these elements. The intentional persistence of an element signature s denoted ( intPersistence ( s )) is expressed as the ratio of the number of occurrences of this element in the set of persistent axioms (denoted nboccurrence ( s , A p^ ) for a version i ) on the total number of persistent axioms. Formally defined:

s ₁< _rel s ₂ iff intPersistence ( s ₁) <  intPersistence ( s ₂) and intPersistence ( s ) = nboccurrence ( s , A p^ )/ 1 A ^p |.

For the detection of consistency principle violations we will discuss some of the most famous methods ([27], [17], [10] and [12]) treating the unsatisfiability of alignment between ontologies.

Authors of Lily [27] define two types of inconsistencies: i. Mappings that form a circle and ii. Mappings that do not meet the equivalentClass / disjointWith axioms mentioned in the original ontology. Therefore the authors use an algorithm that combines the two ontologies to align (the alignment between them is a single graph ( is-a )), and detects the paths which constitute a circle to inform the user of inconsistent mappings by considering them as wrong.

Alcamo’s approach [17] can only ensure the coherence of alignments between ontology TBoxes, by applying preprocessing step to any reasoning activities by removing the ABox of O₁ and O₂ . An iterative algorithm on the entire signature (concepts and properties) of the alignment between two ontologies is proposed to detect unsatisfiable entities. This algorithm detects entities representing unsatisfiable logical consequences of the signature of alignment A between O₁ and O₂ , and checks if they are logical consequences of the signature of O₁ and O₂ . Meilicke [17] identifies the notion of MIPS (Minimal Incoherence Preserving Sub-alignment) and MUPS (Minimal Unsatisfiability Preserving Subalignment), to detect inconsistency and unsatisfiability in a sub-alignment (note that MIPS ( A , O 1 , O 2 ) c MUPS ( A , O₁ , O₂ )), and proposes a variant algorithm (expandand-shrink-algorithm) for debugging incoherent alignments.

ASMOV [10] introduces the notion of mapping validation, a graph built from the alignment and information of the ontologies. Two different constructs constitute this graph: nodes and edges. The nodes contain pairs of entities, whereas the edges contain pairs of properties. The validation process is done in three phases:

concept validation, property validation and conceptproperty validation. In the first two phases, the considered edges (three types: is-a , same-as and disjoint-from ) are created using the predefined properties of the ontology. The validation of the graph is reduced to an investigation of edge violations; a node may not be valid if one or more of the edges are violated. If an edge violation exists, only the linked nodes are investigated.

The detection of consistency principle violations was also studied in LogMap [12]. The core of LogMap is an iterative process that alternates mapping repair and mapping discovery steps. In each iteration, LogMap maintains two structures.

• 1.    A working set of active mappings , which are mappings discovered in the preceding iteration. Mappings found in earlier iterations are established, and cannot be eliminated in the repair step. In the first iteration, the active mappings coincide with the set of anchors.

• 2.    For each anchor, LogMap maintains two contexts (one per input ontology), which can be expanded in different iterations. Each context consists of a set of classes and has a distinguished subset of active classes, which is specific to the current iteration. In the first iteration, the contexts for an anchor C 1 ≡ C 2 are { C 1 } and { C 2 } respectively, which are also the active classes.

Thus, active mappings are the only possible elements of a repair plan, whereas contexts constitute the basis for mapping discovery.

Violations detection alone is not enough. For this, the phase of repairing violations is also of major importance because it ensures us an acceptable quality of alignment.

• C.    Conservativity violation repair

Conservativity violation repair is a process aiming to correct violations, output of the previous detection phase. The goal of this part is to uncover repair strategies used by the systems under study.

The conservativity principle proposed in [13] suggests that the obtained pairs of mappings which lead to violations are in conflict and (at least) one of them in each pairs is likely to be incorrect. Actually, the locality principle4 is proposed to compute a confidence value5 for each conflicting mapping, which can then be exploited for (partially) automating the disambiguation process.

In [23], the detection of conservativity principle violations is done in the same way as LogMap. It uses the mapping (incoherence) repair algorithm presented in [12] and [23] for the extended Horn propositional theories P 1 d and P2 d and the input mappings M. The mapping repair process exploits the Dowling-Gallier algorithm for propositional Horn satisfiability [5] and checks, for every propositional variable A e P 1 d U P2d, the satisfiability of the propositional theory PA = P 1 d U P2d и MU {true ^ A}. Satisfiability of PA is checked in worst-case linear time in the size of PA, and the number of Dowling-Gallier calls is also linear in the number of propositional variables in P 1d U P2d. In the case of unsatisfiability, the algorithm also allows to record conflicting mappings involved in the unsatisfiability, which will be considered for the subsequent repair process. The unsatisfiability will be fixed by removing some of the identified mappings. In the case of multiple options, the mapping confidence will be used as a differentiating factor6.

The signature element that has the less intentional persistent with respect to the relevance relation allows to choose the correspondence to be eliminated from the initial alignment [28]. When two of the signature elements have the same degree of intentional persistence, the choice is left to the user.

Like program debugging, Lily [27] treats all suspicious mappings as two categories: errors and warnings. Apparently, errors are the confirmed wrong mappings, but warnings are the ones which may be wrong, right or imprecise. There are two proposed solutions for the two types of inconsistencies detected by Lily:

• 1.    For i. Mappings that form a circle: authors use an algorithm that combines the two ontologies to be aligned and the alignment between them in a single graph ( is-a ), and goes through the paths which constitute a circle to inform the user of inconsistent mappings by considering them as wrong. The choice to delete one of the arcs

• 2.    For ii. Mappings that do not meet  the

forming the circle is left to the user.

equivalentClass / disjointWith axioms mentioned in the original ontology: Lily proposes two potential solutions: (1) Importing a complex concept and representing the mappings in the form: m : e 1 = e ₂ v e' ₂, such as: ( e 1 ) e ontology O 1 and ( e ₂, e' ₂) e ontology O ₂. (2) Giving the user the choice to delete one of the mappings in conflict.

Note that Lily considers only the mappings between concepts and only equivalentClass / disjointWith as axioms.

In the third phase of the mapping validation process of ASOMV [10], the concept validation graph is modified. All edges are dropped from the remaining valid nodes and are replaced by edges created from the valid nodes of the property validation graph. The new graph is then validated, but in this time the nodes are favored; thus, only the edges are invalidated. All invalid mappings that have been identified are added to the invalid mapping list. If at least one violation was identified, the iteration process resumes and the invalid source-target pairs are ignored.

Concerning the mapping repair in LogMap [12], authors use a Horn propositional logic representation of the extended hierarchy of each ontology together with all existing mappings (both active and established). LogMap splits each ≡ mapping into two Horn clauses (→,←). Thus, for the unsatisfiability checking, LogMap implements the well-known Dowling-Gallier algorithm [5] for propositional Horn satisfiability, and calls the Dowling-Gallier module once (in each repair step) for each class. LogMap takes as input a class C (represented as a propositional variable) and determines the satisfiability of the propositional theory Pc consisting of

• •    the rule ( true → C ),

• •    the propositional representations P 1 and P 2 of the extended hierarchies of the input ontologies O₁ and O₂ , and

• •    the propositional representation   P_M  of the

computed mappings.

• I V. Related Surveys

Several surveys were performed over the last years about alignment maintenance ([4], [7] and [24]).

In this context, [4] provides a thorough survey on mapping maintenance affected by ontologies evolution, by presenting, comparing and discussing existing proposals in different categories (mapping revision, calculation, adaptation and representation). We discuss this survey within its own categorization:

alignment between ontology versions to generate the alignment between the new version and the other ontology. ii. Mapping rewriting in database schemas, works performing mapping adaptation by incrementally rewriting the elements in queries which represent mappings between database schemas. iii. Synchronization of models, scenarios requiring establishing mappings between heterogeneous models like database schemas and ontologies. iv. Change propagation, approaches highlighting the impact of knowledge systems (databases, thesauri, ontologies…) evolution to support the mapping adaptation. v. Mapping change strategies, approaches adapting mappings impacted by knowledge systems changes.

• •    Mapping representation. Proposals in this category focus on representing mappings to support maintenance and alignment with a particular emphasis on user interfaces and mapping description languages.

As strength point, this study succeeded to divide the alignment maintenance problem into relevant subcategories. This categorization lead to separate several issues discussed at the end of the paper:

• •    Knowledge systems evolution. Since information regarding the evolution of knowledge systems remains cornerstone for mapping maintenance, how to correctly and completely invest it?

• •    Mapping interpretation. The semantics of established mappings are poorly interpreted to propose changes in the maintenance process, how to deal with this lack?

• •    Mapping adaptation. How to design efficient adaptation strategies to guarantee that mappings remain valid after suffering ontology changes?

• •    Knowledge systems model. Issues studying interrelated knowledge systems based on heterogeneous models like ontologies and thesauri, or database schemas and taxonomies, whose expressiveness differs substantially.

In return, this analysis has not conducted a comparative study between the investigated systems. Indeed, no metrics proposed in the survey can allow the reader to actually evaluate the advantages and drawbacks of each system. Moreover, the huge expanding of research issues does not really help the search for a significantly advancement, e.g., issues: how to design efficient adaptation strategies to guarantee that mappings remain valid after suffering ontology changes? It cannot be considered as a significant contribution since it just describe the problem and do not trace a new path for research.

• [ 7] presented a comprehensive survey on the notions of alignment Disambiguation and alignment Debugging. An alignment is ambiguous, when some entities are matched with several other entities (assuming that the relation is equivalence), e.g., a ?:? alignment is expected but a *:*

alignment has been returned. A simple method for dealing with this problem is to always choose the correspondence with the higher confidence (greedy algorithm). An alternative solution is to suppose that the correct match among two classes is prone to have other correct matches among its more general and more specific entities [26]. Alignment debugging aims at restoring consistency and coherence of the produced alignment. Consistency is characterized by the aligned ontologies having no models. Coherence is characterized by no model of the aligned ontologies allowing a particular class to have instances. In this category the authors present the most famous systems (LogMap [12], ASMOV [10], ALCOMO [17]) with other less known systems:

• •    ContentMap [11] can be considered as a constraint-based debugging tool with the constraints provided by users. It aims at helping users to understand and evaluate the consequences of the integration of two ontologies as well as to identify and handle possible errors.

• •    [15] used a naive Bayes [9] classifier for learning

how to generate disjointness axioms in order to apply ontology repair techniques through inconsistency detection. Such a classifier is trained on various data sets and uses different similarity features (path distance, shared properties, similarity, instance sets) of pairs of classes, for deciding which ones are disjoint.

• •    [30] proposed restoring consistency only within

spheres, which are local sets of ontologies and alignments.

Alignment Evolution has been also studied in [7]. According to the authors, managing alignments requires keeping them available in servers and making them evolve if necessary. Usually, alignment evolution corresponds to the creation of a new alignment, derived from an existing one. In this survey the different cases in which the alignment evolution is required are shown:

• •    Alignment evolution should be recorded within the alignment metadata (Annotations of alignments, or alignment metadata, record useful information for retrieving alignments or for explaining them) in addition to changes in the structure.

• •    An alignment may also evolve because it is no longer useful, being superceded by another one, or more generally, by the addition of further qualification to an alignment.

• •    Alignment evolution may also be triggered either by adding or by discarding correspondences manually produced, or by better methods, since new information is available.

• •    As soon as ontologies evolve, new alignments have to be produced following the evolution of the ontology. This can be achieved by transforming the changes made to ontologies into an alignment (from one ontology version to the next one), which

can be composed with the old alignment to obtain an updated alignment.

Another survey is presented in [24]. In this analysis, the author discusses detecting and correcting conservativity principle violations in ontology mappings by presenting the problem statement based on works of [12]. Several works dealing with the conservativity principle have been presented in this survey according to two categories:

• 1.    Approaches introduced the notion of Assumption of Disjointness:

• •    [22] originally introduced the assumption of

disjointness to address the repair of ontologies underspecified in terms of negative constraints.

• •    [25] applied the assumption of disjointness in the

context of repairing ontology mappings, and limited the number of disjointness axioms to be inserted by using learning techniques.

• •    In [8] the authors present an interactive system to guide the expert user in the manual enrichment of the ontologies with disjointness axioms.

• 2.    Ontology matching systems dealing with the conservativity principle: in this part, authors presented three systems as example ASMOV [10], Lily [27] and YAM++ [19] which implemented different heuristics to avoid violations of the conservativity principle. In  addition, another

relevant approach [1] presents a set of sanity checks and best practices  when computing ontology mappings.

To accomplish the comparison of different surveys performed on alignment maintenance, the following table (Table 5) summarizes the different problems studied in each survey.

Table 5. Comparison between different surveys according to the studied problems.

	Studied problem
Approach	Satisfiability Preservation Problem	Ontology change Preservation Problem	Conservativity Problem
[7]	Alignment Debugging	Alignment Evolution	Not studied
[24]	Approaches introducing the notion of Assumption of Disjointness	Not studied	Ontology matching systems dealing with the Conservativity Principle
[4]	Mapping revision	Mapping calculation Mapping adaptation	Not studied

• V.    Statistics

The current section includes some statistics about approaches and surveys studied in this paper. The first figure (Fig 1) presents the number of articles (most of papers are cited in [20]) produced for each approach.

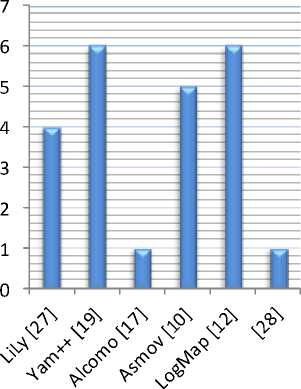
u Number of articles

Fig.1. Number of articles produced for each approach

Fig 1 shows that the approaches [19] and [12] were the subject of the highest number of scientific productions. The smallest number of papers was devoted to the approaches [10] and [28].

Fig 2 is a bar graph including the number of proposed approaches for each sub-problem of the conservativity principle. Whereas Fig 3 shows the amount of open research questions for the conservativity principle suggested by each analysis studied in our survey.

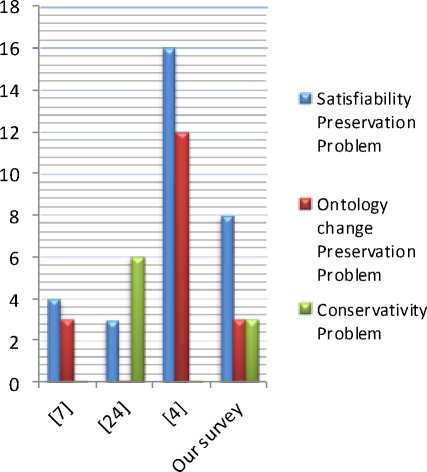
Fig.2. Number of proposed approaches for each conservativity sub-problem

Fig 2 shows that in [4] we find the largest number of the proposed approaches to address the problem of "Satisfiability Preservation" and "Ontology change Preservation". In our survey, we focus on the problem of "Conservativity" which is not presented in any of the other surveys.

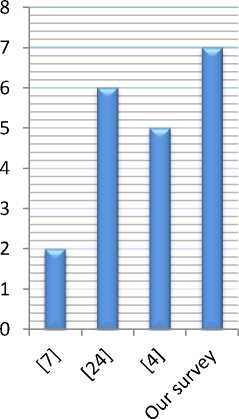
и Number of open questions

Fig.3. Number of open research questions suggested by each studied analysis

It is clear in Fig 3 that our survey provides the highest number of open problems in the field of "Conservativity Principle Violations".

• VI.    Conclusion and Research Challenges

This study allows pointing out open key issues, which existing approaches, addressing the conservativity principle, have neglected. Our main observation relies on the fact that literature did not deal with the conservativity principle problem in an effective and complete manner. The two main approaches identifying the conservativity of mappings ([13] and [23]) between ontologies have been a subject of many neglected logical consequences. First, they take only the source ontology and the alignment in consideration, and discard the target ontology in the process of detecting conservativity principle violations. Second, they also deal with conservativity principle violations only at the concept hierarchy level within the input ontologies, and therefore, drop out the others possible types of violations.

We still consider as research challenges the following questions:

• Violation treatments. Which appropriate methods could be applied to face the conservativity principle violations of alignment between ontologies? What are the possible ways to reduce the conservativity problem to a consistency problem which will allow reusing the available infrastructure and techniques for the mapping repair?

• •    The impact of violations. Which consequences may have an alignment violating the conservativity principle in different application scenarios? Which impact could violations have on the aligned ontologies? What is the degree of the violations propagation? And which metrics can we use to measure this impact?

• •    The cost of repairing mappings. What is the cost needed to address conservativity principle violations?

• •    Algorithm performance. Which is the trade-off between completeness and runtime for these algorithms?

There are probably other research questions about the conservativity problem, but we consider that these issues are of great importance to ensure the quality of alignments between ontologies.