Construction of High-accuracy Ensemble of Classifiers

Published Online April 2014 in MECS

Classifier systems based on the combination of outputs of a set of different classifiers have been proposed in the field of pattern recognition as a method of developing high performance classification systems [1]. In ensemble method for classification, many classifiers are combined to make a final prediction [2]. Ensemble methods show better performances than a single classifier in general [3]. The final decision is usually made by voting after combining the predictions from set of classifiers.

So far different ensemble learning algorithms have been proposed like Adaboost, Bagging and Arcing. Adaboost and Arc-x(h) are two ensemble algorithms that belong to Arcing family of algorithms. For h = 4, Arc-x(h) performs equally well as Adaboost. They use different weight updating rules and combine classifiers using different voting schemes [4]. By far, the most common implementation of Boosting is AdaBoost, although some newer algorithms are reported to achieve better results.

An ensemble has a vital need for diversity, that is if an ensemble of classifiers is to be good as a plural classification, they should be diverse as enough as to cover each other’s' errors. Consequently, while constructing an ensemble, we need a mechanism to guarantee the diversity of the ensemble. Sometimes this mechanism is in a way that a basic classifier is selected or removed from ensemble to maintain the diversity of the ensemble. In ensemble-based learning, it is possible that the data is fractioned into smaller parts and afterward a simple and quick model is created for each part. In this regard, final ensemble model is performed in a way without significant time overhead. To learn any problem, many classifiers have been introduced so far [5]. Each of the proposed classifiers has strengths and weaknesses that make it suitable for specific problems. Nevertheless ensemble based learning is a powerful approach to provide an optimal classification system for each problem. The most challenging issue in constructing an ensemble based classification system is how constructing a proper ensemble of base classifiers [6].

In researches discussed in [7, 8], fuzzy k-means algorithm has been used for clustering the classifiers. The partitioning is done considering the outputs of classifiers on train dataset as feature space. From each partition, one classifier is selected to participate in final ensemble. Furthermore, in these approaches, each classifier is examined over the whole train dataset and its accuracy is calculated based on the results.

Selecting an appropriate classifier from each cluster is not investigated in the previous researches. This issue can highly effect on the accuracy of classification tasks.

In this paper, we introduce a new approach for constructing ensembles. It firstly makes base classifiers. Afterward k-means clustering algorithm is employed to partition classifiers. Then some classifiers are selected from clusters to construct the final ensemble. This approach utilizes Bagging and Boosting algorithms as producers of basic classifiers. We proposed three selection methods to select a classifier from each cluster. One of the aims of this study is to investigate whether it is possible not to select any classifier from some specific clusters and achieve a superior ensemble. To justify this situation, it has to be mentioned that in clustering of a typical dataset, some of clusters are created for a null data or some noisy data. In this paper, we investigate the effect of removing these clusters and also the effect of sampling rate of training data on the efficiency of classifiers. In our proposed approach, in order to reach the diversity required among primary classifiers, every one of them was trained with random sampled data. The volume of sampled training data is b percent of total training data. Generally, in Bagging method, the value of parameter b is always 100, but in our proposed method, to produce basic classifiers, the parameter value is set to a number between 30 and 100. Our experiments illustrated that selecting the most accurate classifier among each cluster, is led to the ensemble with highest accuracy. The most proper values for the number of clusters and the sampling rate were determined by different experiments. Furthermore, the experimental results illustrate the effectiveness of our proposed approach.

The organization of this paper is as the follows: In the second section, related works are discussed. Proposed approach is explained in Section 3 and experimental results are described in the fourth section. Section 5 includes conclusion.

• II.    Related Works

Ensemble learning is a powerful approach to provide any problem with an almost optimal classification system. Generally it is true that combining different classifiers leads to increase in classification efficiency [9,10]. This shows the importance of diversity in an ensemble's success. Diversity among basic classifiers signifies their independence. This means that failure in classification of basic classifiers will not take place simultaneously on one template. Kuncheva in [11] has shown that, theoretically and practically, an ensemble of some basic classifiers always increases classifications'

accuracy if basic classifiers are independent. It has also been shown that ensemble philosophy can be also applied to Bayesian networks [12]. Kuncheva has proposed some methods to measure an ensemble's diversity and then has suggested a model to build a diverse ensemble based on a search method [13].

Application of clustering classifiers has been discussed in [14, 15]. In previous works, classifiers in the ensemble have performed their learning process randomly and each one is constructed based on the entire training set. It has been proved that combining classifiers in the ensemble are more efficient than individual ones in average [17]. Since classifiers with different features or different methodology can complement each other and cover each other's disadvantages, combining methods often lead to improve classification efficiency [6]. Kuncheva in [18] demonstrates by kondorset theorem that usually a combination of classifiers, performs better than a single one, i.e. if different classifiers are used in combination, their total error may notably decrease. In the neural network field, several methods for the creation of ensembles of neural networks have been investigated [19]. Such methods basically lie on varying the parameters related to the design and training of neural networks.

Several techniques have been proposed to create diversity. For example different subsets of training samples are created and after that independent classifiers are created upon them. Bagging and Boosting methods are the most famous methods for creating ensembles [20, 21]. In these methods, rather than using all the samples, their subsets are used to train basic classifiers. The term Bagging is first used by [5] abbreviating for bootstrap aggregating. In Bagging idea, the ensemble is made of classifiers built on bootstrap copies of the train set. Using different train sets, the required diversity for ensemble is obtained. In order to promote model diversity, Bagging trains each model in the ensemble using a randomly-drawn subset of the training set [20]. Fig. 1 illustrates the training phase of Bagging method in general. Boosting involves incrementally building an ensemble by training each new classifier to emphasis the training instance that previous classifiers misclassified [21, 22].

In another level, features are used to produce diversity among classifiers, in a way that each classifier uses a subset of features [18, 9, 23]. In a different viewpoint, different kinds of classifiers are used in combination to make diversity [11]. In the mentioned methods, if we create many classifiers, there is a possibility that some of them always give the similar output. Therefore, after creating some classifiers with a given method, a selection mechanism should be applied to select appropriate classifiers and our proposed approach offers some solution to this issue.

• III.    Proposed Approach

The main idea of our proposed approach is combining classifiers based on the most diverse subsets of basic classifiers. In the first phase, some basic classifiers are produced based on two famous mechanisms of creating ensembles, Bagging and Boosting. Then produced classifiers are partitioned by a clustering algorithm according to their outputs on the entire set of training data. Fig. 2 shows the block diagram of the proposed approach, which uses k-means clustering algorithm for portioning base classifiers.

After constructing a large number of basic classifiers, proposed approach partitions them with the help of k-means clustering algorithm. Then the selection phase is triggered. This section involves three different selection methods. In the first method, a classifier is selected randomly from each cluster. In the second method, the most accurate classifier in each cluster is selected and in the third one, the nearest classifier to the center of each cluster is used for constructing the final ensemble.

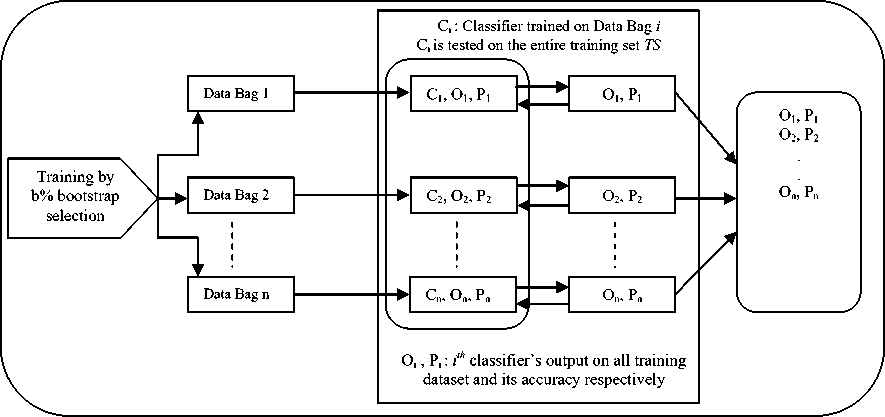
Fig. 1: Training phase of Bagging method

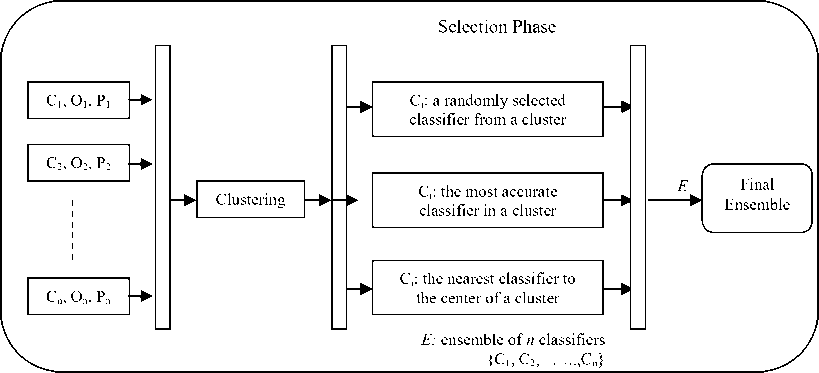
Fig. 2: Block diagram of the proposed approach

Since each cluster is created based on the outputs of classifiers, it is so likely that by selecting one classifier from each cluster and employing it to construct an ensemble, the formed ensemble is a diverse one and has better performance than ensembles created by original Bagging and Boosting approaches.

The pseudo code of the proposed approach in training part is shown in Fig. 3. In this figure, Bagging technique is used to create basic classifiers.

Input:

TS : Training Set

L: Labels of Training Set

• n: Ensemble Size

• b: Ration of Sub samplings from TS

Output:

• E: Ensemble of Classifiers

P: Accuracies of Classifiers

• O:    Outputs of Classifiers

m=size ( TS )

for i = 1: n

DB i = subsample ( TS , b)

Train ( C i , DB i )

for j = 1: m

O (i, j) = Test ( C i , TS (j))

end

P(i) = Accuracy of C i

E(i) = Ci end

Fig. 3: The pseudo code of proposed approach, training phase n subsets of training set are provided by sampling without displacement. ith data subset, which is b% of training set and obtained by sampling, is called ith data bag and is shown as DBi. This is obvious that the number of samples in DBi is m*b/100 where m is the number of all samples in dataset TS. Then a basic classifier is trained on each DBi and classifier trained on DBi is called Ci. Afterward, Ci is tested on the entire training set TS and its accuracy is calculated. The output of ith classifier on jth data from TS is a vector shown by Oij. Okij is the degree of ith classifier's certainty that jth data belongs to kth class. ith classifier's output on all training datasets is shown by Oi and its accuracy is shown by Pi. One of the differences between approaches of producing basic classifiers in proposed method and Bagging method lies in sampling rates. In Bagging method, the value of sampling rate, b, is always 100 but in our proposed approach, to produce basic classifiers the parameter value is set to a number between 30 and 100.

In the following, we will describe the methods proposed to employ in selection phase of the presented approach.

• 3.1    Random selection Mechanism

The pseudo code of the proposed approach by selection a classifier randomly from each cluster is shown in Fig. 4. In this method, the clusters that have less than two classifiers are deleted. Then from each cluster, a classifier is chosen randomly. SC is ensemble classifier and SP is accuracy of the classifier. In the framework of the proposed method, a set of samples DC is created at first in which, each sample is a classifier. The i^th sample of DC is the i^th classifier. Assume that our data has f features. P^th feature of i^th sample is shown as X ip , that is obtained from (1):

k ip        ij

where j and k are calculated by (2) and (3), in which c is the number of classes.

j=Гp / c 1

k = p - j * c

Input:

• E: Ensemble of Classifiers

• P: Accuracies of Classifiers

O: Outputs of Classifiers th: Threshold of Selecting a Classifier

Output:

SC: Ensemble of Classifiers

SP: Accuracies of Classifiers

SOC: Size of Cluster

[n m] = size (O)

C = K-means (O, r)

Cluster of Classifiers (1: r) = {} for i = 1: n

CC (i) = CC (i) u {C(i)}

Acc_C(i) = Acc_C (i) и {P(i)} end j=0

for i = 1: r

SOC = | CC (i) | if (SOC > th)

j=j+1

Temp = Random Select (1: SOC)

SC (j) = CC (temp)

SP (j) = Acc_C (temp)

end end

Fig. 4: The pseudo code of the proposed approach using random selection mechanism

Features of DC dataset are viewpoints of different basic classifiers on main dataset's data. So we have a new dataset with n data (each of which is a classifier) and f features ( F=m*c ). Parameter n , which is a predefined parameter by user, is the number of classifiers produced by Bagging or Boosting approaches. After creating dataset DC , we divide it to many partitions by a clustering algorithm. The number of partitions is shown by r .

Classifiers in a partition have similar outputs. This means that they have low diversity. So it is better to select one classifier from each cluster. In order to avoid null classifications, clusters with fewer members than a threshold th are omitted. Assume that E is an ensemble of n classifiers { C 1 , C 2 _C_n } and there is c classes in the problem. Assume that by applying the ensemble on data O j , a matrix D^j similar to (4) is resulted:

D ^j

O 1 1 j	O 2 1 j	1 .           nj
. Оc - 1 O 1 j	. Оc - 1 2 j	.. .   0c - 1 .          nj
c O 1 j	c O 2 j	c .     O nj

Now ensemble decides whether data O j belongs to class q according to (5):

cn q = argmax 2 wk * D k i=1 k=1

in which w k is the weight of k^th classifier, and in optimal situation computed by (6) ^[11]:

pk

wk=log 1-7

where p k is the weight of k^th classifier which effects on training set TS . Notice that in equal terms we use random function in (5). Assume vector L^j for data O j , L^j O is one if O j belongs to class q and is zero if not. Now the accuracy of classification C k on TS is calculated from (7).

mc

22 L i - O U

j=1i=1           1

c x m

• 3.2    Accurate Selection Mechanism

In this selection method, the algorithm selects the most accurate classifier from each cluster. Pseudo code of the proposed selection method is shown in Fig. 5.

Input:

• E: Ensemble of Classifiers

• P: Accuracies of Classifiers

O: Outputs of Classifiers th: Threshold of Selecting a Classifier

Output:

SC: Ensemble of Classifiers

SP: Accuracies of Classifiers

SOC: Size of Cluster

[n m] = size (O)

C = K-means (O, r)

Cluster of Classifiers (1: r) = {} for i = 1: n

CC (i) = CC (i) ^ {C(i)}

Acc_C(i) = Acc_C (i) и {P(i)} end j=0

for i = 1: r

SOC = | CC (i) | if (SOC > th)

j=j+1

tmp = ar g max..-cy- Acc_C(x)

SC (j) = CC (temp)

SP (j) = Acc_C (temp)

end end

Fig. 5: Pseudo code of the proposed approach by selecting most accurate classifiers from each cluster

• 3.3    Center-cluster Selection Mechanism

The concept of classifiers clustering is reaching to more diversity. To provide more diversity, we proposed to choose the classifier which is the most closest to the center of each cluster. The Pseudo code of the proposed approach using this selection mechanism is shown in Fig. 6.

Input:

• E: Ensemble of Classifiers

• P:    Accuracies of Classifiers

• O: Outputs of Classifiers

th: Threshold of Selecting a Classifier

Output:

SC: Ensemble of Classifiers

SP: Accuracies of Classifiers

SOC: Size of Cluster

[n m] = size (O)

[C, Centers] = K-means (O, r)

Cluster of Classifiers (1: r) = {} for i = 1: n

CC (i) = CC (i) и {C (i)}

Acc_C (i) = Acc_C (i) и {P (i)} end j=0

for i = 1: r

SOC = | CC (i) | if (SOC > th)

j=j+1

temp=argmin _{x e C} c(i) Distance(O, Center(i))

SC (j) = CC (temp)

SP (j) = Acc_C (temp)

end end

Fig. 6: Pseudo code of the proposed approach employing center-cluster selection mechanism

Until now, three methods for selecting classifier from each cluster have been described. To evaluate the performance of the proposed approach, we ran experiments on 18 representative datasets from the UCI repository. In this paper, the measure of performance employing different selecting methods is achieved for classifying the datasets. Furthermore, the effect of sampling rate and the number of clusters is investigated.

• IV.    Experiments

In this section, experimental results of employing our proposed approach using some standard datasets are reported. Accuracy of the classifiers is calculated by 4fold-cross-validation method. A short explanation of datasets used in this research is given in Table 1.

Table 1: Short explanation of the examined datasets

Data set	Number of classes	Number of features	Number of instances
Iris	3	4	150
Wine	3	13	178
Yeast	10	8	1484
SA-Heart	2	9	462
Breast Cancer	2	9	683
Bupa	2	6	345
Glass	6	9	214
Galaxy	7	4	323
Half-Ring	2	2	400
Ionosphere	2	34	351
Balance Scale	3	4	625
test Monk1	2	6	412
test Monk2	2	6	412
test Monk3	2	6	412
train Monk1	2	6	124
train Monk2	2	6	169
train Monk3	2	6	122

All datasets are extracted from Machine Learning website [1] except for Halfring dataset which is handmade and is considered as a difficult dataset for machine learning algorithms [8]. All parameters of classifiers are constant during creation of an ensemble.

Decision tree (DT) is one of the most versatile classifiers in the Machine Learning field. Decision tree is considered as one of the unstable classifiers that can be suitable for ensemble construction. It uses a tree-like graph or model of decisions. The kind of representation is appropriate for experts to understand what classifier does [26]. Its intrinsic instability can be employed as a source of diversity in classifier ensemble. The ensemble of a number of DTs is a well-known algorithm called Random Forest (RF), which is one of the most powerful ensemble algorithms. The algorithm of Random Forest was first developed by Breiman [5]. In this paper, DT is totally used as base classifier. Criterion of decision tree is Gini criterion and parameter of pruning is set to 2.

The Multi-Layer Perceptrons (MLP), the most representatives of artificial neural network, is a linear classifier for classifying data specified by parameters and an output function. Its parameters are adapted similar to stochastic steepest gradient descent. The units each perform a biased weighted sum of their inputs and pass this activation level through a transfer function to produce their output, and the units are arranged in a layered feed forward topology. The network thus has a simple interpretation as a form of input-output model, with the weights and thresholds (biases) the free parameters of the model. Important issues in MLP design include specification of the number of hidden layers and the number of units in these layers [24]. One way is to set the weights explicitly, using a prior knowledge. Another way is to 'train' the MLP, feeding it by teaching patterns and then letting it change its weights according to some learning rule. In this paper, the MLP is used as one of the base classifiers.

Number of hidden layers in neural network classifiers is set to 2 and the number of neurons in each layer is respectively 10 and 5 neurons. In each layer of the neural network, functions 'tansig', 'purelin' and 'logsig' is used.

Gianito [25] imply a clustering and selection method to deal with the diversity generation. In that work, at first, a large number of classifiers with different initializations are produced, and then a subset of them is selected according to their distances in their output space. This research doesn’t take into consideration how the base classifiers are created.

In Table 2, the accuracy of the proposed approach using Bagging, Boosting and Gianito with sampling rate of 30%, appropriate cluster threshold of 2 and basic classifiers of neural networks has been shown. The fifth column shows the Gianito method [25]. As shown from the sixth column (from left to right) with the proposed approach using selection of the most accurate classifiers from clusters and Bagging method, higher performance is achieved compared to the other methods. The eighth and ninth columns, respectively, shows the results of experiments using the proposed approach with the algorithm presented in Fig. 5 and Bagging and Boosting generators. The tenth and eleventh columns show the results of proposed approach using random selection of classifiers from each cluster and employing of Bagging and Boosting generators.

Table 3 shows the results of repeated experiments of Table 2 using decision trees as weak classifiers. What was concluded from Table 2 can be seen here too. As the results illustrated, the proposed approach with Bagging algorithm has great advantage over other ones. The degree of this advantage is higher here than what resulted from Table 2. This is for rather instability of basic classifiers of decision tree compared to artificial neural networks. The bold value in the row of each dataset shows the highest accuracy.

Table 2: Accuracy of different classification (%) with approaches of Bagging, Boosting and Gianito, sampling rate of 30%, appropriate cluster threshold of 2 and basic classifiers are neural networks

Dataset	Ada Boost	Arc-X4	Bagging (Random Forrest)	Cluster and Selection (Gianito)	Classifier Selection
					Bagging (Most Accurate Classifier Selection)	Arc-X4 (Most Accurate Classifier Selection)	Bagging (CenterCluster Selection)	Arc-X4 (CenterCluster Selection)	Bagging (Random Classifier Selection)	Arc-X4 (Random Classifier Selection)
Iris	94.67	96.62	96.62	93.33	98.66	97.32	97.32	95.32	97.97	97.33
Wine	94.38	96.59	96.06	95.23	98.3	97.74	97.18	96.62	97.19	95.51
Yeast	59.50	60.85	61.19	60.56	59.82	60.64	60.04	61.18	61.19	60.85
SA-Heart	69.48	73.04	72.39	70.18	71.64	70.98	71.64	71.20	71.52	71.09
Breast Cancer	96.49	97.06	96.91	96.19	97.36	97.36	97.06	96.92	96.91	96.47
Bupa	68.41	70.06	71.22	71.98	66.08	68.40	67.82	67.82	72.09	68.02
Glass	66.36	66.04	66.98	67.05	69.62	67.28	67.74	66.34	67.45	66.04
Galaxy	85.14	87.00	85.62	87.00	85.74	86.68	85.12	85.74	85.62	84.52
Half-Ring	97.25	97.25	95.75	97.25	97.24	97.25	97.24	97.24	97.25	97.25
Ionosphere	89.17	90.03	88.51	88.51	95.14	94.3	95.72	96.28	90.31	87.64
Balance Scale	93.12	93.27	91.99	95.75	93.92	92.32	92.16	94.24	91.35	92.95
Monk problem1	98.99	98.06	92.23	98.34	100.00	98.78	98.54	98.04	98.43	97.87
Monk problem2	87.48	87.35	85.68	87.21	85.42	87.62	87.62	87.36	87.41	87.23
Monk problem3	96.84	97.09	95.87	96.77	99.26	98.78	96.84	97.32	97.33	96.99
Average	85.52	86.45	85.50	86.10	87.02	86.90	86.58	86.56	86.57	85.70

Table 3: Accuracy of different classification (%) with approaches of Bagging, Boosting and Gianito, sampling rate of 30%, appropriate cluster threshold of 2 and basic classifiers are decision trees.

Dataset	Ada Boost	Arc-X4	Bagging (Random Forrest)	Cluster and Selection	Classifier Selection
					Bagging (Most Accurate Classifier Selection)	Arc-X4 (Most Accurate Classifier Selection)	Bagging (Center Cluster Selection)	Arc-X4 (Center Cluster Selection)	Bagging (Random Classifier Selection)	Arc-X4 (Random Classifier Selection)
Iris	94.67	96.62	95.27	94.59	96.66	94.66	95.32	95.32	96.62	95.95
Wine	96.63	96.07	97.19	92.61	97.18	93.82	97.18	97.74	97.19	95.51
Yeast	54.78	53.17	53.98	54.51	55.32	55.98	54.78	53.22	53.98	52.09
SA-Heart	67.32	70.00	71.30	68.04	73.58	71.2	72.06	67.52	72.61	69.70
Breast Cancer	96.19	95.74	96.32	93.68	95.90	95.02	96.48	95.46	96.47	95.05
Bupa	66.96	70.64	72.09	64.53	72.74	74.48	72.46	71.30	72.97	66.28
Glass	70.09	65.04	70.28	60.85	71.48	65.42	70.08	70.08	70.28	62.26
Galaxy	71.83	70.59	73.07	70.94	72.12	72.74	72.74	72.74	72.45	70.28
Half-Ring	97.25	97.25	95.75	95.75	97.25	96.74	96.50	96.00	97.25	95.75
Ionosphere	91.17	90.31	92.31	87.64	92.30	95.14	92.02	92.02	91.45	89.74
Balance Scale	91.52	94.44	93.60	94.44	93.60	97.60	94.24	94.56	94.72	94.24
Monk problem1	98.03	98.11	97.49	98.34	97.08	98.04	98.54	98.78	98.76	97.37
Monk problem2	91.65	97.01	86.64	97.14	100.00	87.62	97.32	87.12	97.62	86.73
Monk problem3	95.51	87.29	96.92	87.31	99.26	92.22	96.84	87.12	96.97	96.34
Average	84.54	84.45	85.16	82.88	86.71	85.17	86.27	84.21	86.38	83.38

As expected, according to the experimental results,     approaches. This was not unexpected because increasing performance is improved by employing our proposed     the accuracy and diversity of the various classifiers, enhance the accuracy of ensembles. Besides using the most accurate classifiers form each cluster as representative, the proposed approach was led to greater efficiency. If we choose the best classifiers from each cluster, both criteria have been satisfied to make successful ensemble. Fig. 7 shows the effect of number of clusters and sampling rate on the performance of clustering algorithm using decision tree classifiers, Bagging generator on Iris, Bupa and Breast cancer datasets. The results illustrate that number of clusters greater than 11 lead to accuracy reduction. The reason is that the clusters are sparse and clustering them actually loses its meaning. As noted in this Fig. 7(b), the classification accuracy by increasing the sampling rate to 50% is encountered with increase, but after that, it reduced.

For example in the Iris dataset, up to the sampling rate of 50%, the accuracy is increasing. This increment is not constant, therefore it can be concluded that from sampling rate 10% up to 50%, accuracy uniformly and ascending is enhanced. Also with incrementing the number of clusters from 3 to 11, accuracy is increasing.

For Bupa dataset, up to the sampling rate of 50% the accuracy is increasing and this increment almost up to sampling rate of 70% continues but after that, the accuracy is reduced significantly. With increasing the number of clusters from 3 to 5, almost accuracy remained constant but then up to 11, the accuracy increment is significant.

In the Breast cancer dataset, up to the sampling rate of 50%, the accuracy is continuously increasing and thereafter accuracy increment is not permanent. With growing the number of clusters up to 9, accuracy is also increasing and it remained almost constant from 9 to 11 and then declined. Therefore, from the results it can be concluded that the best sampling rate is 50% and the best number of clusters is 11. Number of clusters more than 11, causes clusters to be scattered and decreases the accuracy.

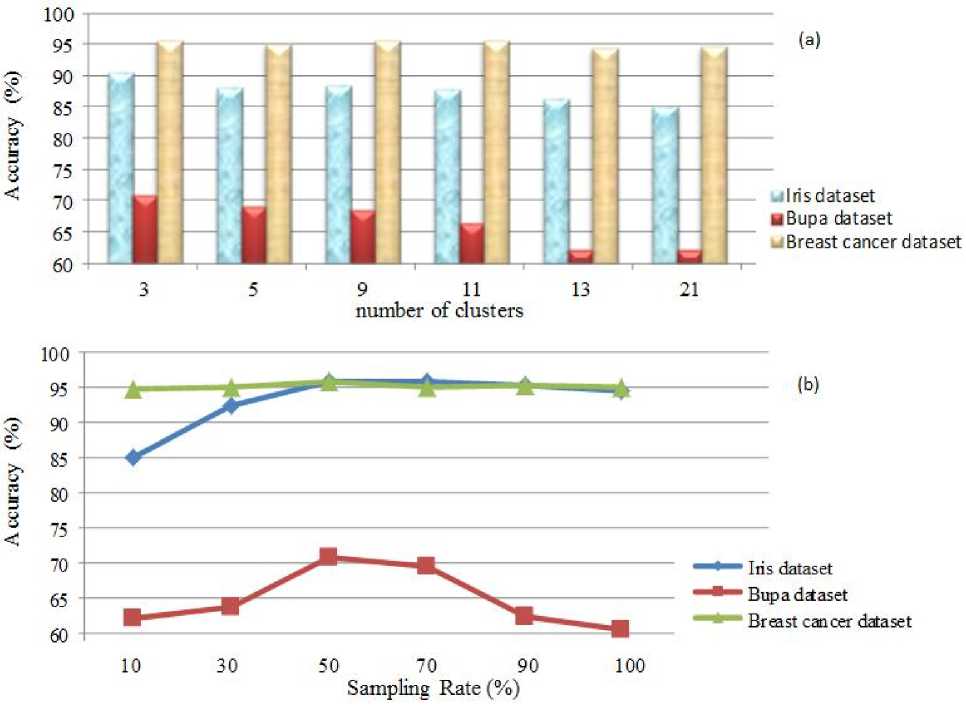
Fig. 7: (a) Effect of number of clusters (b) Effect of sampling rate on the performance of accurate selection method; Selection of most accurate classifiers from each cluster using decision tree as basis classifiers, Bagging generator and n=151(number of classifiers)

Fig. 8 shows comparison between average accuracy of Bagging and Boosting, considering effectiveness of the number of classifiers and sampling rate that respectively are setting to (31, 51, 101, 151) and (10, 30, 50, 70, 90, 100). As previously mentioned, using Bagging generator, performance of the proposed method is more highlights.

It is understood from Fig. 8 that employing Bagging generator in all selection methods results better than applying Boosting generator. Fig. 8 shows that the best sampling rate for both Bagging and Boosting generators is 50%.

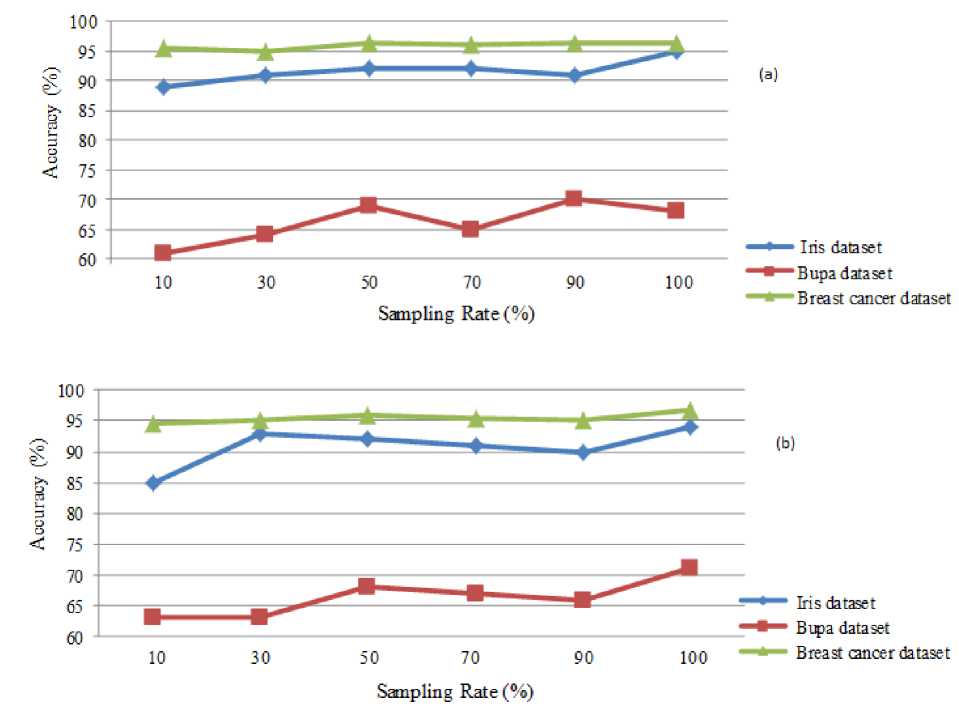
Fig. 8: Comparison of the average accuracy using Bagging and Boosting in all the selection methods with effectiveness of sampling rate by decision tree basis classifiers, (a) Average accuracy of Bagging on Iris, Bupa and Breast cancer datasets (b) Average accuracy of employing Boosting generator on Iris dataset, Bupa and Breast cancer datasets

• V.    Conclusion

In ensemble construction, all clustering and selection methods suffer from selecting an appropriate classifier from each cluster. In our proposed approach, the main goal is increasing the accuracy of classification. The accuracy of an ensemble could depend on sampling rate and number of clusters. In previous works, employing Bagging and Boosting methods, the value of sampling rate is always set to 100. In our proposed approach, we investigated the effectiveness of different values of sampling rate on the accuracy of final constructed ensemble. Type of basic classifiers is decision tree or multi-layer neural networks. After constructing a large number of basic classifiers, our approach clusters them employing k-means clustering algorithm. Afterward, three selection methods are proposed for choosing proper classifiers from clusters. Furthermore, in this paper the effect of number of clusters on the performance of ensembles was investigated. The experiments demonstrate that sampling rates more than 50% not only do not increase classification accuracy but also decrease it. Moreover, the number of clusters greater than 11 lead to reduce accuracy. The reason is that the clusters get sparse and clustering them actually loses the meaning. Proposed approach with Bagging algorithm has great advantage over other ones. Experimental results show that picking the classifiers with highest accuracy from each cluster results the ensemble with the highest accuracy. Clustering ensures ensemble diversity and the best classifiers are selected from clusters, to have an accurate and varied ensemble.