Construction of Strength Two Mixed Covering Arrays Using Greedy Mutation in Genetic Algorithm

Published Online September 2015 in MECS DOI: 10.5815/ijitcs.2015.10.04

In a highly configurable software product, it is necessary to test the interaction among various configuration parameters to avoid interaction errors. For instance, in a system with n configuration parameters each of which can take m possible values, an exhaustive test set will have mn test cases to check all possible combinations of configuration parameters. The number of test cases increases exponentially with the increase in number of configuration parameters. Thus, exhaustive testing of highly configurable software may be impractical due to the limitation of budget and time required to generate and run large sized test sets. An alternative to exhaustive testing is combinatorial interaction testing (CIT) as introduced in [1] which samples the set of configurations in such a way so as to test all possible t-way ( t denotes the strength of testing) combinations of configuration parameters. The size of test set grows at most logarithmically in CIT with the increase in number of configuration parameters compared to the exponential growth in case of exhaustive testing [1].

Pair-wise testing is a CIT technique that tests all possible pair-wise (2-way) combinations of configuration parameter values. Pair-wise testing drastically reduces the size of test set as compared to exhaustive testing, without losing significantly on the fault detection capability [2]. Empirical studies show that test set covering all possible 2-way combination of configuration parameter values is effective for software systems [1, 3, 4]. In further work, Burr and Young [5] provided more empirical results to show that pair-wise test coverage is effective. In [6], Dalal et al. presented empirical results to argue that testing of all pair-wise interactions in a software system finds a large percentage of the existing faults. Kuhn et al. [7] examined fault reports for many software systems and concluded that more than 70% of the faults are triggered by two-way interaction of configuration parameters.

Covering Arrays (CAs) and Mixed Covering Arrays (MCAs) are combinatorial objects that correspond to test set in software testing. To perform effective pair-wise testing, there is a need to construct an optimal 2-way CA/MCA. The problem of finding a minimal t-covering array is NP-complete [2, 8]. Therefore, the main focus of researchers in the field of CIT is to find an effective technique to construct an optimal CA/MCA. Metaheuristic search based optimization techniques have being used by researchers to generate an (near) optimal CA/MCA. Metaheuristic techniques need longer run time than their greedy counterparts; however, greedy techniques usually need larger samples to exercise the same set of interactions [9].

In this paper we use GA to generate optimal CA/MCA for pair-wise testing. The purpose of this paper is to explore the effect of different mutation strategies on the overall performance of GA to construct (near) optimal

CAs and MCAs for pair-wise testing. The work presented here is an extension of our previous work [10] wherein the performance of GA to generate CAs/MCAs for pairwise testing was improved by using a greedy approach to perform value occurrences mutation, a smart mutation technique introduced by Flores and Cheon [11]. Smart mutations select the genes for mutation based on some selection criteria and replace them with some predefined values as compared to random mutation in which genes for mutation are selected randomly and are replaced by randomly selected values. In this paper an algorithm to improve the performance of smart mutation and a technique to perform mutation using greedy approach is proposed.

The remainder of this paper is organized as follows. Section 2 gives the necessary background on combinatorial objects. Section 3 gives an overview of GA. Section 4 presents various methods available to construct CAs and MCAs. Section 5 describes the proposed greedy approach to improve the performance of smart mutation in GA and presents a new greedy algorithm to perform mutation. Section 6 describes the implementation of the proposed greedy approach using an open source tool PWiseGen [12] and presents experimental results to show the effectiveness of the proposed greedy approach. Section 7 concludes the paper and future plans are outlined.

• II.    Combinatorial Objects

This section gives an overview on combinatorial objects. CA and MCA are combinatorial objects with applications in several areas such as drug screening, data compression, GUI testing [13], web-application testing applications [14, 15], regression testing [16] and highly configurable system testing [17]. In CIT, a CA/MCA is constructed in such a way so as to cover each t-way combination of parameter values at least once. The effective application of CAs and MCAs in various fields has motivated researchers to find effective ways to construct optimal CA/MCA.

• A.    Orthogonal Arrays

An orthogonal array OA λ (N; t, k, v) is an N × k array on v symbols such that every N × t sub-array contains all ordered subsets of size t from v symbols exactly λ times and they have the property λ = N/v^t [18]. The use of OA in the field of software testing is limited due to the restrictions imposed on OA that all parameters have same number of values and that each pair of values be covered the same number of times [19]. In general, the OA is difficult to generate and its test suite is often quite large. But OA has its advantages, such as making it relatively easy to identify the particular combination that caused a failure [20]. To complement OA construction and to overcome its restrictions CA and MCAs have been introduced.

• B.    Covering Arrays

A covering array [21] denoted by CA λ (N;t,k,v), is an

N × k two dimensional array S on v symbols such that every N × t sub-array contains all ordered subsets from v symbols of size t at least λ times. If λ = 1, it means that every t-tuple needs to be covered only once and we can use the notation CA(N; t, k, v). N is the number of rows of S, k is the degree that represents the number of parameters and v is the order which represent the number of values each parameter can take and t is the strength that corresponds to the degree of interaction between parameters. An optimal CA contains minimum number of rows to satisfy the properties of the entire covering array. The minimum number of rows is known as covering array number and is denoted by CAN (t, k, v). A test set can be represented by a CA of size N× k where each row corresponds to a test case. Each column represents an input parameter and the values in the column represent the domain of the respective input parameter.

• C.    Mixed Covering Arrays

A mixed covering array [22] denoted by MCA (N; t, k, (v₁v₂ …v_k)), is an N × k two dimensional array, where v₁, v 2, …, v k is a cardinality vector which indicates the values for every column. An MCA has the following two properties: 1) Each column i (1 ≤ i ≤ k) contains only elements from a set S i with | S i | = v i and 2) The rows of each N × t sub- array cover all t-tuples of values from the t columns at least once. The minimum N for which there exists an MCA is called mixed covering array number and is denoted by MCAN (t, k, (v₁ v₂ …v_k)). A shorthand notation can be used to represent MCAs by combining equal entries in (v i : 1 ≤ i ≤ k). An MCA (N; t, k, (v 1 v 2 …v k )) can be represented as MCA (N; t, k, (w₁^q1w₂^q 2 .. w s ^qs)), where k = E ^s ₌₁ q i and w , | 1 < j < s {v₁ v₂  …v_k}. Each element w j ^qi in the set

(w₁^q1w₂^q2 ….w_s^qs) means that q_i parameters can take w j values each. A MCA of size N × k can be used to represents a test suite with N test cases for a system with k input parameters each with varying domain size. We use the notation r i for all 1 ≤ i ≤ N, to represent a row of CA/MCA.

• III.    Genetic Algorithm

GA is a metaheuristic stochastic method that is inspired by the Darwinian evolution and is used to solve search based optimization problems. GA has been successfully applied for solving large number of optimization problems due to its robustness and easy-to-use nature [23]. In GA, a population of candidate solution is initialized and evolves towards increasingly better regions of the search space by means of evolutionary operators like selection, crossover and mutation, until a satisfactory solution to the problem is found or a stopping criterion (maximum number of iterations) is met. Each individual in the population has a fitness value which is calculated using the fitness function. This fitness function is a function of the objective that we want to optimize. As compared to traditional search algorithms, GA is more flexible and can be applied to a wide range of applications as it uses only the evaluation of the objective function regardless of its nature. Also GA starts searching using a population of points instead of a single point (as done in case of traditional approaches) thus covering the search space thoroughly and avoids the chances of getting stuck in the local minima [24]. The efficiency of GA depends on many parameters such as initial population, selection strategy and recombination operators (crossover, mutation). The adaptation of GA parameters and operators has become an important research area in the field of GA. Over a decade much research has been done in applying adaptive mutation operators to guide the search of GA towards optimum solution.

Having described the notations, in the next section we will briefly discuss the existing state-of-the-art algorithms for constructing optimal CA/MCA for pair-wise testing.

• IV.    Related Work

Existing state-of-the art algorithms for constructing (near) optimal CAs and MCAs are broadly classified into algebraic, greedy, metaheuristic and random methods. Algebraic methods are generally used by mathematicians. There are two approaches to construct CAs using algebraic methods. The first approach to construct CA is based on the construction of OA, where OA is derived from some mathematical functions [19, 25]. The second approach is based on the concept of recursive construction where larger CA is constructed from smaller CA [26, 27]. Despite the fact that algebraic methods are fast, their use in the field of CIT is often limited due to the restriction imposed on OA that each parameter must have same number of values [28]. Finally, constraint handling [29] can be more difficult in algebraic methods.

Greedy algorithms have been the most popular method among software testing community to construct CAs. The algorithms used to construct CAs using greedy approach are classified as: one-test-at-a-time and one-parameter-ata-time. In one-test-at-a-time approach, CA is constructed one row at a time and the algorithms using this approach usually differ in the way rows are constructed. The well known strategies under this approach are Automatic Efficient Test Generator (AETG) [3], Test Case Generation (TCG) [30], Classification-Tree Editor eXtended Logics (CTE-XL) [31], Jenny [32], Pairwise Independent Combinatorial Testing (PICT) [33], Deterministic Density Algorithm (DDA) [34, 35], Intersection Residual Pair Set Strategy (IRPS) [36]. In case of one-parameter-at-a-time approach, CA is generated for the first two parameters, and then it is extended to generate CA for the first three parameters, and continues to do so for each additional parameter [2, 37]. The strategies that have adapted this approach are IPOG [28], IPOG-D [28, 38] and IPO-s [39].

Recently metaheuristic techniques such as Simulated Annealing (SA) [22, 40, 41, 42, 43, 44], Hill Climbing(HC) [22], Tabu Search (TS) [45, 46, 47], Ant Colony Optimization (ACO) [48], Particle Swarm Optimization (PSO) [49, 50, 51, 52, 53, 54, 55] and GA [10, 11, 48, 56, 57, 58, 59, 60] have been explored by researchers to generate CAs/MCAs. In [61], Stardom first compared SA, TS and GA to construct CAs of strength-2 showing SA to be the most efficient of all three. Cohen et al. [22] used SA and HC to construct CAs and MCAs of strength-t (t ≤ 3) and the experimental results showed that heuristic techniques outperformed greedy methods for strength-2 CAs but they failed to give superior results for higher strength CA especially for t = 3. A comparison between SA and HC shows that while they produced similar lower bound, but SA outperformed HC in the number of trials required to generate the solution. Later on, numerous methods [40, 41, 42] have been proposed by Cohen et al. that use a combination of different methods (for e.g. algebraic method and computational search) to generate uniform covering array and variable strength covering array. The existence of constraints in a system makes CIT difficult as the generated CA may contain some combination of parameter values which are invalid. Hence, careful handling of such constraints is desirable. In [62], Garvin et al. extended SA algorithm to construct CAs for constrained interaction testing. Satisfiability (SAT) solver have been used by Hnich et al. [63], Yan and Zhang [64] and Banbara et al. [65] to generate t-way CA. Calvagna and Gargantini [66] use SAT modulo theory (SMT) solvers to handle constraint during the construction of CIT samples. Calvagna and Gargantini [67, 68] presented a logic based approach to generate CA for pair-wise test coverage. Finally, in case of random methods, test cases are selected randomly from the complete set of test cases based on some input distribution. They are mainly used for comparison with other test suite generation algorithms to study the effectiveness and the failure detection ability of the proposed approach [69].

• V.    The Proposed Approach

The process of generating optimal CA/MCA for pairwise testing using GA begins by creating an initial population of CAs/MCAs of size N × k randomly that represents possible solutions to the given problem. Initially N is unknown hence there are two ways to start the search process. One way is to set a loose lower and upper bounds on the size of an optimal array and then use a binary search process to find a smallest size CA/MCA [61]. Second method is to start with the size of a known CA/MCA and search for a solution. This method requires less computational resources, but the size of the CA/MCA must be known in advance. In this paper we use the second method to generate optimal CAs/MCAs, where N is chosen from the reported results (best bound achieved) in the existing state-of-the-art. After initialization, the fitness of each individual CA/MCA is evaluated using a fitness function which is defined as the number of distinct pair of parameter values covered by the CA/MCA. Then selection, crossover and mutation operators are applied iteratively to evolve the initial solution towards better solution. Mutation has a significant effect on the performance of GA as mutation avoids getting stuck in the local minima and maintains diversity in the population. In traditional GA, every individual has an equal probability of getting mutated irrespective of their fitness [24]. Thus the probability of an individual with highest fitness to be disrupted by mutation is equal as compared to the one with lowest fitness. Hence a mutation strategy is needed to mutate an individual to maximize improvement in fitness by minimizing fitness loss due to mutation.

In this paper an effort is made:

• (i)    To present a greedy approach to improve the performance of pair occurrences mutation and similarity mutation [11].

• (ii)    To present a new greedy algorithm to perform mutation in GA for construction of optimal CA/MCA for pair-wise testing.

• A. Improved_Pair Occurrences Mutation

In pair occurrences mutation [11], pairs of parameter values that are not present in the CA/MCA selected for mutation are inserted in place of pairs which occur more than once in the CA/MCA, in an attempt to increase the fitness of the CA/MCA. When an existing pair is replaced with an uncovered pair, two cases may arise:

• (i)    One-value replacement – In this case only one value of an existing pair needs to be replaced to accommodate the uncovered pair.

• (ii)    Two-value replacement – In this case both values of an existing pair needs to be replaced to accommodate the uncovered pair.

During mutation, in addition to the gain of new pairs that are formed by the insertion of an uncovered pair, there may also be a loss of few existing pairs that are formed by the combination of values of the pair which are selected for replacement. For instance, if we consider a MCA (9, 2, 5, 2¹3²4¹5¹) shown in Fig. 1, it can easily be found that the pair ‘a1 a2’ is not covered by the given MCA. When examining the MCA it is found that the pair ‘a1 c2’ has maximum number of occurrences and hence the existing pair occurrences mutation replaces the first instance (row r 3 in our case) of ‘a1 c2’ by ‘a1 a2’ . This is the case of one-value replacement, where only the value of parameter P2 is replaced. Initially row r₃ covers c2 a1, c2 a3, c2 c4 and c2 b5 pairs with respect to the parameter P2’s value c2. After replacing c2 by a2, the pairs covered by r 3 with respect to a2 are a2 a1, a2 a3, a2 c4 and a2 b5 . Out of these four pairs, pair a2 a3 has also been covered by row r 9 of the MCA. Hence after replacement, the MCA covers three new pairs: a2 a1, a2 c4 and a2 b5 . However, there is also a loss of two pairs: c2 a3 and c2 c4 since these pairs were covered by only row r₃ before pair occurrences mutation was performed. The improvement in the fitness of MCA after pair occurrences mutation denoted by F improved (MCA) is calculated using (1). The improvement in fitness in this case is one.

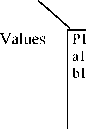
Input Parameters

P2   P3  P4   P5

a2   a3  a4   a5

b2  b3  b4   b5

c2  c3  c4   c5

d2 d4

e4

" al  b 2  b 3  a 4

bl  b 2  a 3  c 4

a l ^ c 2 a 3 c 4 b 5

a2 -"al  c2  c 3  b 4

replaces bl  b 2  b 3  a 4

al  c 2  c 3  b 4

bl  c 2  c 3  d 4

al  d 2  b 3  d 4

bl  a 2  a 3  e 4

Fig. 1 Pair Occurrences Mutation

F improved ( MCA ) = Number of new pairs gained - Number of old pairs lost

As an existing pair is replaced by a missing pair in either one-value replacement or two-value replacement, there are three possible cases that can occur during replacement: best, worst and average case. In the best case we assume that there will be a gain of maximum possible number of new pairs (k-1) in one-value replacement and (2k-3) in two-value replacement whereas the loss will be minimum (ideally zero) in both the cases. In the worst case we assume that in both the cases, there will be a gain of only one pair which was not covered by the MCA before mutation. However, a maximum loss of (k-2) pairs in case of one-value replacement and (2k-4) pairs in case of two-value replacement will occur. So the improvement in fitness in all the three cases for one-value replacement and two-value replacement is given by (2) and (3) respectively:

f (k — 1)      | best case

• ^{—(k —} 3) I wor^{st case}

—(k — 3) <  x < (k — 1) | average case

1 (2k — 3)      | best case

• ^{—(2k —} 5)  | ^{worst case}

—(2k — 5) <  x <  (2k — 3) | average case

Here, we propose a technique to maximize Fimproved(MCA) by minimizing the loss of existing pairs during pair occurrences mutation. This is achieved by using greedy approach to select a row rmin in which loss due to either one value or two values replacement is minimum. In one-value replacement, to find rmin we consider rows ri | 1 ≤ i ≤ N as candidate rows which contain the pair having maximum occurrences. We list the pairs covered by each candidate row with respect to the value that is to be replaced. Then the listed pairs of each candidate rows are compared against each other and if a row is found that covers no distinct pairs then it is selected for replacement. If no such row is found, the listed pairs of each candidate rows are compared with the remaining rows of the MCA and the candidate row ri covering least number of distinct pairs is selected for replacing value during pair-occurrences mutation. In two-value replacement the same procedure is repeated, except the way the pairs are listed. Now we list all the pairs covered by both values of the pair which occurs maximum number of times and select the row which covers least number of distinct pairs. When we apply improved_pair occurrences mutation in the example given in Fig. 1, it is found that row r6 covers no distinct pairs as shown in Fig. 2, so we select row r6 instead of row r3 to minimize the loss of existing pairs and thus maximize the fitness of the MCA by four.

Values

Input Parameters

P1  P2  P3  P4P5

a1  a2   a3   a4a5

b1  b2  b3  b4b5

c2   c3   c4c5

d2 d4

Pairs Covered by: r 3 : c2 a 1, c2 a3, c2 c4, c2 b5 r 4 : c2 a 1, c2 c 3, c2 b4 , c2 c5 r 6 : c2 a1, c2 c3 , c2 b4 , c2 b5 r^ -----------

Covers no distinct pairs

a 1 b 1

a 1 a 1

b 1 a 1

c 2 d 2 a 2

b 1

a 1

b 1

b 2 b 2 c 2 c 2 b 2 c 2

a2 replaces c2

b 3 a 3 a 3 c 3 b 3 c 3 c 3 b 3 a 3

a 4 c 4 c 4 b 4 a 4 b 4 d 4 d 4 e 4

b 5 a 5 b 5 c 5 a 5 b 5 a 5 b 5

a 5

^ improved (MCA')

( k (k — 1)/2      | best case

—(2kn — n² — n)/2)  | worst case

—(2kn — n² — n)/2 < x < k(k — 1)/2 laverage case

Where, n is the numbers of positions in which the two rows differ.

In this paper, we propose a technique to maximize F_improved(MCA) by minimizing the loss of existing pairs during similarity mutation. A greedy approach is used to select from the two or more similar rows, a row which covers least number of distinct pairs within the given MCA. An example is shown in Fig. 3 to illustrate the effect of similarity mutation and improved_similarity mutation. Test Cases represented by row r 2 and r 4 of MCA (10, 2, 6, 4²3²5¹2¹) in Fig. 3 are similar (for similarity threshold=65%). In similarity mutation, r₄ will get replaced with a new test case that causes a loss of five existing pairs which were not covered by any other row of the given MCA. When we apply improved_similarity mutation, row r 2 and r 4 are compared with every row of the given MCA and it is found that row r 2 covers less number of distinct pairs as compared to row r 4 , hence row r₂ is replaced instead of row r_4, resulting in loss of less number of distinct pairs as compared to those in similarity mutation. It is clear from Fig. 3 that the improvement in fitness achieved by improved_similarity mutation will be higher than that of similarity mutation.

MCA (9, 2, 5, 21324151)

Fig.2. Improved_Pair Occurrences Mutation: Comparison of rows of MCA to find a row that covers minimum number of distinct pairs

Input Parameters

P1 P2 P3 P4 P5 P6 a1 a2 a3 a4 a5 a6 b1 b2 b3 b4 b5 b6 c1 c2 c3 c4 c6 d1 d4 d6

B. Improved_Similarity Mutation

In case of similarity mutation proposed by Flores and Cheons [11], if two test cases (rows) in the test set (CA/MCA) are (almost) similar (greater than or equal to a predefined threshold), the second test case is replaced with a new test case with an aim of improving the fitness of the test set. The parameter values for the new test case can be selected either randomly or for each parameter the value which occurs minimum number of times in the CA/MCA is selected. If the two test cases are 100% similar, then there will not be any loss of existing pairs during replacement otherwise there are chances that some pairs that were exclusively covered by the second test case might get lost during replacement. As explained in case of pair occurrences mutation, the improvement in fitness in best, worst and average case during similarity mutation is given by (4).

r2 gets replaced in case of improved^, Г bl b 2 a 3 a 4 b 5

similarity mutation ~ 0 i b 2 a 3 _c 4 b 5

r 7 gets replaced in case of MDPM

c 1 c 2 a 3 d 4 a 5 a 1 b 2 a 3 c 4 a 5 d 1 c 2 a 3 a 4 b 5 c 1 b 2 b 3 c 4 b 5 c 1 c 2 b 3 a 4 b 5 c 1 a 2 c 3 a 4 a 5 a 1 c 2 b 3 e 4 a 5

d 1 b 2 b 3 a 4 a 5

Comparison of pairs covered by r 2 and r 4 wrt their dissimilar elements (for similarity /improved similarity mutation) with the pairs covered by the remaining (N-2) rows of MCA

r 2	r 4
b5 a1	a5 a1
b5 b2	a5 b2
b5 a3	a5 a3
b 5 c4	a5 c4
b 5 a6	a5 d6
a6 a1	d6 a1
a 6 b2	d6 b2
a6 a3	d6 a3
a6 c4	d6 c4

Los s : 2 Loss:5

b 6

a 6

a 6

d 6

d 6 a 6 b 6 b 6 b 6 c 6

r 4 gets replaced in case of similarity mutation

Fig.3. Comparison of Similarity, Improved_Similarity and Minimum Distinct Pairs Mutation

• C. Minimum Distinct Pairs Mutation (MDPM)

Algorithm: Minimum Distinct Pairs Mutation (MDPM)

begin select a MCA for mutation set flag = true while (flag = = true)

set flag = true replace ri in MCA with a new row end if end while end

• Fig.4. Algorithm to perform MDPM

In this section we propose a greedy technique to perform mutation known as minimum distinct pairs mutation (MDPM). As described above, in case of similarity mutation we replace a similar test case, but it may happen that there are no test cases (rows) which satisfy the similarity threshold criteria. In that case similarity mutation cannot be performed. However, there may be a test case which is not similar to any other test case in the given MCA, but still makes no contribution towards the fitness of the MCA. In MDPM we replace the test case which makes minimum contribution (ideally zero) towards the fitness of MCA by covering least number of distinct pairs as compared to the remaining test cases in the MCA. A MDPM threshold needs to be defined here, which allows MDPM to occur only if the number of distinct pairs covered by the test case is below the MDPM threshold value. The MDPM threshold prevents good test cases to be unnecessarily distorted by mutation. During MDPM, the parameter values for the new test case can be selected either randomly or for each parameter the value which occurs minimum number of times in the CA/MCA is selected as in case of similarity mutation. For instance, in the example shown in Fig. 3, row r7 is not similar to any other row of the MCA (for similarity threshold = 65%). However when we list all pairs covered by r7 and compare them with pairs covered by the remaining (N-1) rows of the MCA, it has been observed that row r7 doesn’t cover any distinct pair with respect to the remaining (N-1) rows. Hence, we replace r7 by a new test case. The objective of MDPM is to maximize the improvement in fitness of MCA after mutation by minimizing the losses. It can be seen from Fig. 3 that row r4 gets replaced after similarity mutation causing a loss of five pairs, row r2 gets replaced after improved_similarity mutation reducing the loss to two pairs whereas row r7 is replaced after MDPM dropping the loss to zero pair. One point that is to be noted here is that the performance of MDPM is comparable to similarity/ improved_similarity mutation if two rows in the MCA are 100% similar. An algorithm to perform MDPM is given in Fig. 4.

The improvement in fitness during MDPM in best, worst and average case is given by (5).

( к (к — 1)/2      | best case

0               | WOT^{st case}

0 <  x <  к(к — 1)/2 | average case (5)

The advantage of MDPM over similarity and improved_similarity mutation is its performance in average and worst case. It is observed from (5) that in average and worst case, the quality of MCA generated after MDPM doesn’t deteriorate as may happen in case of similarity and improved_similarity mutation.

• VI. Computational results

To assess the practicality of the work presented in this paper, we have implemented the proposed approaches using an open source tool PWiseGen. PWiseGen is an extensible, reusable and configurable tool written in Java to generate pair-wise test set using GA [11]. We have extended PWiseGen by adding to it the capability to perform improved_pair occurrences mutation, improved_similarity mutation and MDPM and name it PWiseGen-GM (Greedy Mutation). First, we present the results of experiments carried out to compare the performance of existing smart mutations with the proposed improved smart mutations. Next, we compare the performances of improved smart mutations with MDPM. Finally we compare the performance of PWiseGen with MDPM with the existing state-of-the-art algorithms.

Experiments are carried out on the dataset given in Table 2. The dataset consists of benchmark problems selected from the existing state-of-the-art [22, 43, 52, 54, 70] for generating both CAs and MCAs.

For achieving the best performance of PWiseGen-GM it is necessary to choose suitable values of GA parameters. There exists evidence in literature that the choice of probability of crossover pc and probability of mutation pm plays a critical role in the performance of GA. A number of guidelines for setting the values of pc and pm exist in literature [23, 71, 72]. Typical values of pc are in the range 0.5~1.0, while typical values of pm are in the range 0.001~0.05. In addition to the parameters mentioned above, population size and number of generations influences the performance of GA. A large population size will use more computational resources without obtaining better solutions, whereas a small population size may leads to the under-covering of search space thereby guiding the algorithm towards poor solutions. Similarly a large number of generations may consume more time, whereas a smaller number of generations will make the algorithm terminate early, preventing it to converge to a good solution. Hence in accordance with the existing GA literature, we set the population size to 50, pc to 1 and pmto 0.05 during the experimentation. We perform experiments with varying number of generations on some selected benchmark problems from Table 2, but no significant improvements on quality of the final solution were observed after 20,000 generations in all the cases. Hence we set the number of maximum generations to 20,000.

Table 1. Dataset

Sno.	Benchmark	k(number of	Total number
	Problems	input parameters)	of pairs
1	33	3	27
2	34	4	54
3	3 5	5	90
4	36	6	135
5	37	7	189
6	3 8	8	252
7	3 13	13	702
8	510	10	1125
9	1020	20	19000
10	2 100	100	19800
11	4 100	100	79200
12	2233	5	67
13	4534	9	454
14	513822	11	492
15	273241102	12	837
16	7 2 6 2 4 2 3 2 2 2	10	854
17	2 13 4 5	18	992
18	82726252	8	1178
19	6 4 4 5 2 7	16	1556
20	5 1 4 4 3 11 2 5	21	1944
21	6151463823	19	1992
22	624929	20	2052
23	6 5 5 5 3 4	14	2074
24	7 1 6 1 5 1 4 5 3 8 2 3	19	2175
25	694327	19	3000
26	674823	18	3004
27	4 15 3 17 2 29	61	14026
28	4 1 3 39 2 35	75	17987

• A.    Improved Smart Mutations versus Smart Mutations

In this section we present the result of experiments carried out to compare the performance of a) improved_pair occurrences mutation and pair occurrences mutation and b) improved_similarity mutation and similarity mutation. In both the cases, first we plotted the fitness of the generated CA/MCA against the generation number. Second, we made a comparison between the fitness of best CA/MCA generated by the existing smart mutation techniques and the proposed improved smart mutation techniques. As GA produces non-deterministic results, so to have a better statistical significance, each benchmark problem is executed 30 times and the average value is noted. The result of comparison of improved_pair occurrences mutation and pair occurrences mutation is shown in Fig. 5 and Fig. 6. Due to space reason, we show the experimental results of a few benchmark problems selected as representative, from the dataset of Table 1.

700 680

Fitness 660 640 620 600

Im prove d_P air Occurrences Mutation

Pair Occurrences Mutation

Num ber ofG enerations

Im prove d_P air Occurrences Mutation

P a ir О c currenc e s Mutation

19850 4 C

Fitness 15,zl00 ritness 19250

Number of Generations

1 170

1 140

1 1 10

Fitness 1050

990 960

Fitness 17600

МСА^^^бЪ^)

Improved_Pau Occurences Mutation

Pair Occurences Mutation

Number of Generations

МСА^З3^3^)

Im proved_Pair Occurences Mutation

Pair Occurences Mutation

Number of Generations

Fig.5. Comparison of quality of CA/MCA generated versus number of generations in pair occurrences mutation and improved_pair occurrences mutation

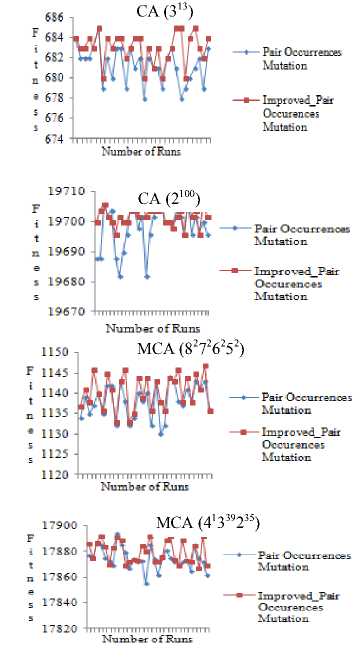
Fig.6. Comparison of quality of generated CA/MCA using pair occurrences mutation and improved_pair occurrences mutation

It is clear from Fig. 5 that improved_pair occurrences mutation generates CA/MCA in less number of generations than pair occurrences mutation. Also, it is evident from Fig. 6 that the quality of CA/MCA generated using improved_pair occurrences mutation is better than that of pair occurrences mutation. The result of comparison of improved_similarity mutation and similarity mutation is shown in Fig. 7 and Fig. 8.

It is evident from Fig. 7 and Fig. 8 that the CA/MCAs generated using improved_similarity mutation generates better quality CA/MCA by covering more number of distinct pairs in less number of generations as compared to similarity mutation.

Number of Generations

MCAfS^^2)

■:: i

2 / ULI

Nurn b er of Ct enerations

MCA(41531722£>)

Number of Generations

1 3900

1 J -ULi

Improved Similarity

Mutation

Similarity Mutation

Improved Similanty

Mutation

Similanty Mutation

Improved Similanty

Mutation

Similanty Mutation

Improved Similanty

Mutation

Similarity Mutation

МСА(б9432Э

Fig.7. Comparison of quality of CA/MCA generated versus number of generations in similarity mutation and improved_similarity mutation

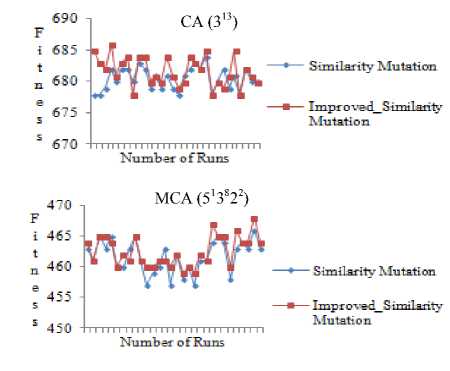
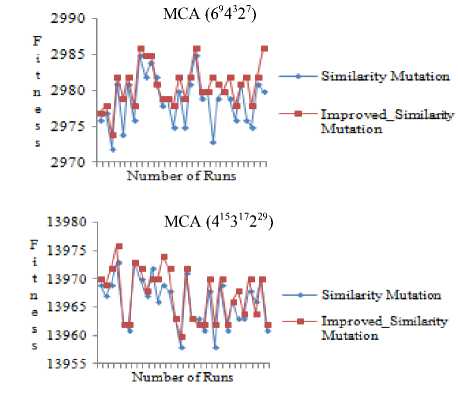
Fig.8. Comparison of quality of generated CA/MCA using similarity mutation and improved_similarity mutation

• B.    Comparison of MDPM and Improved Smart Mutations

In this section, we present the result of experiments carried out to evaluate the performance of MDPM with respect to the improved smart mutations techniques proposed in Section 5 and in [10]. Each benchmark problem given in the dataset of Table 2 is executed 30 times on PWiseGen-GM using various improved smart mutations techniques and MDPM. The average of the values obtained over 30 runs for each of the benchmark problem is plotted as shown in Fig. 9. It is evident from Fig. 9 that MDPM outperforms improved smart mutation techniques by generating better quality CA/MCA. The performance of improved_value occurrences mutation is comparable to the performance of improved_pair occurrences mutation except in few cases where improved_pair occurrences mutation outperforms improved_value occurrences mutation. For small size problems, the performances of all the four mutation strategies are identical (benchmark problems: 33 and 34).

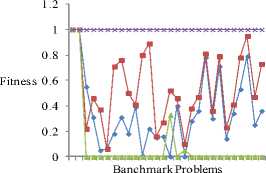
—•— Improved_Value Occurrences Mutation

—■— Improved_Pair

Occurrences Mutation

—*— Improved_Similarity Mutation

—X  MDPM

Fig.9. Comparison of MDPM with improved smart mutation techniques

• C.    Comparison Results

In this Section we compare the performance PWiseGen-GM with MDPM with the existing state-of-the-art algorithms. The comparison is made on two criteria’s: array size and array generation time. As array generation time is dependent on the system configuration, so to ensure a fair comparison, we restrict our comparison against publicly available tools namely Jenny [32], Pairwise Independent Combinatorial Testing PICT [33], ACTS (IPOG) [73], AllPairs [74]. These algorithms are run on Windows using an INTEL Pentium Dual Core 1.73 GHZ processor with 3.00 GB of memory. The result of comparison made on the dataset of Table 2 with respect to CA/MCA array size and the array generation time (in seconds) is shown in Table 3.

As it can be seen from Table 3, PWiseGen-GM with MDPM outperforms the existing techniques for generating CA/MCA for pair-wise testing in most of the configurations. In cases where PWiseGen-GM (MDPM) doesn’t generate best results, it still gives competitive performances than the existing strategies. It is evident from the results shown in Table 3 that PWiseGen-GM (MDPM) requires more time to build CAs/MCAs than Jenny [32], ACTS (IPOG) [73] and AllPairs [74] in average; however, the extra time consumed by PWiseGen-GM (MDPM) allowed the construction of CAs/MCAs of smaller size as compared to those generated using other strategies.

• VII. Conclusion and Future Work

In this paper, we have examined the impact of mutation strategy on the performance of GA used to construct CAs/MCAs for pair-wise testing. First, we have proposed few improvements to the existing smart mutation techniques. Secondly, we have proposed a greedy approach to perform mutation. Experiments performed on a set of benchmark problems indicate the effectiveness of the proposed approach in terms of quality of generated CAs/MCAs and the number of generations in which the solution is achieved, when compared to the existing smart mutation techniques. Comparison with the existing state-of-the-art algorithms shows that the proposed approach outperforms the existing approaches in most of the cases in terms of CA/MCA size.

In future, we plan to find out how effectively the proposed greedy algorithm can be applied to construct higher strength CAs/MCAs. Furthermore, we also plan to construct CAs/MCAs that can handle constraint between various configuration parameters of the system under test.

Table 3. Comparison of PWiseGen-GM (MDPM) with the existing state-of-the-art algorithms.

The * shows that PWiseGen with MDPM performs best in these cases.

Id.	Dataset	Jenny	PICT1	ACTS	AllPairs	PWiseGen-GM
	3 3			(IPOG)		(MDPM)
1		9/0.015	10	9/0.003	9/0.015	9/0.0624
2	34	11/0.015	13	9/0.002	9/0.016	9/0.078
3	35	14/0.031	12	15/0.016	14/0.016	11*/0.078
4	36	15/0.046	14	15/0.015	14/0.015	12*/0.109
5	3 7	16/0.046	16	15/0.014	14/0.014	13*/1.201
6	38	17/0.046	16	15/0.016	14/0.016	14/2.13
7	3 13	18/0.062	20	19/0.014	17/0.016	16*/10.45
8	510	45/0.062	47	45/0.003	47/0.15	43*/40.29
9	10 20	193/2.308	216	227/0.53	219/0.015	210/ 792.8
10	2 100	16/0.249	16	16/0.078	15/0.11	13*/6.24
11	4 100	53/2.527	56	57/0.093	59/0.109	55/901.8
12	2233	12/0.015	10	9/0.003	10/0.016	8*/5.678
13	4 5 3 4	26/0.031	26	24/0.001	25/0.015	21*/1.95
14	5 1 3 8 2 2	23/0.031	20	19/0.002	20/0.016	16*/6.302
15	273241102	106/0.327	100	100/0.016	100/0.016	100/1.232
16	7262423222	57/0.078	56	53/0.001	54/0.009	53/5.896
17	2 13 4 5	26/0.124	23	24/0.015	27/0.014	20*/14.617
18	8 2 7 2 6 2 5 2	76/0.093	80	72/0.003	76/0.009	70*/8.502
19	644527	53/0.109	55	44/0.006	48/0.012	44/15.069
20	514431125	32/0.093	32	26/0.015	29/0.011	26/10.052
21	6 1 5 1 4 6 3 8 2 3	40/0.03	38	36/0.016	37/0.01	34*/17.534
22	624929	44/0.109	41	39/0.016	40/0.016	38*/6.38
23	655534	56/0.124	59	56/0.015	55/0.008	54*/103.10
24	716151453823	50/0.140	46	43/0.016	42/0.018	44/14.08
25	694327	64/0.187	67	61/0.016	67/0.014	60*/32.07
26	6 7 4 8 2 3	63/0.171	63	54/0.016	59/0.014	54/145.54
27	4 15 3 17 2 29	39/0.405	38	33/0.031	36/0.019	33/170.75
28	4 1 3 39 2 35	31/0.436	29	28/0.016	27/0.028	25*/316.04