Context-aware recommendation methods

Published Online September 2018 in MECS

In this age of internet of things, big data and cloud computing, users are constantly overloaded with a large number of products and services that makes it challenging for them to choose the best-suited products and services. Recommender systems help users make decisions on what to purchase or consume online by estimating the preference of users and suggesting the products and services that fit their profile based on some historical data.

A recommender system takes the ratings of different users to extract their preferences and provide recommendations. It is also an information filtering system that predicts the rating or rank that a user would give to an item. A recommender system uses a recommendation algorithm to filter items, by predetermining how a specific user might rate or rank them based on historical rating pattern of the user or other similar users.

The process of recommendation is similar to searching for relevant items based on a query input and ranking the results based on user's historical activities. Thus, the problem of providing recommendations is similar to a search ranking problem [1].

Psychological research has shown that certain psychological factors and conditions affect the behaviors of humans [2]; the author in [2] assumes the same for the effect of context in generating recommendations. Traditional recommendation systems use 2-dimensional data consisting of only users and items, ignoring additional contextual information during their recommendation process. In contrast, context-aware systems incorporate the factors, conditions and the characteristics of the environment that affect users. Location, time, weather and activities are few examples of these factors [3].

Context-aware recommender systems are systems that incorporate contextual information, e.g., weather, location, mood, season, etc., alongside the core data (users and items) to generate better recommendations. Some research has shown that incorporating seasonality and weather contexts into recommender system produces better recommendations [4]. We can relate to how differently we feel in different seasons and how some activities are tied to seasons and weather conditions. For instance, certain products are not available in certain seasons, and some activities are only available in a particular kind of weather.

Some examples in [5], presents certain applications where traditional recommendation systems might fall short. An example of such scenario is a news application that recommends different news based on the day of the week. Here, “the day of the week” is a contextual information that should be incorporated into the recommender system. A news recommender application that suggests news based on the day of the week is a good example of a context-aware recommender system that filters and segments recommendation based on the context information that affects the likability of an item [5]. This shows the tremendous influence that context has in improving the quality of recommendation.

We aim to develop two context-aware recommendation approaches that use coupled matrix factorization and show that it performs better than some of the existing context-aware methods. Our proposed methods are contextual-driven, in the sense of making context front and center of our recommendation approaches and not just a factor in improving recommendation.

This paper is organized as follows. Section II discuss some related works in the area of context-aware matrix factorization and coupled matrix factorization. Section III provides a discussion of recommender systems. Section IV discusses context-aware recommender systems. In section V, we provide a discussion of our proposed methods. In section VI, we offer an evaluation of our proposed methods and discuss extensively the results obtained. In section VII and VIII, we make some conclusions and present, future works.

• II.    Related Works

In this chapter, we do a review of some works on recommender systems that used context-aware matrix factorization in their process of generating recommendations. After that, we discuss related works on coupled matrix factorizations.

• A.    Context-Aware Matrix Factorization Methods

In [6], some context-aware matrix factorization (CAMF) techniques were developed to capture the interaction between the ratings and some contextual factors. The methods proposed by the authors measure the relevance of the contextual factors on the ratings based on three different assumptions. Three models were developed to capture the influence of each contextual condition on the user ratings.

The first model in [6] is called CAMF-C; it assumes that each contextual condition has a uniform influence over all the items. That is, the effect of each contextual condition over user ratings is the same for all items. A single parameter represents the effect for all items in a contextual condition. The total number of parameters is the sum of all contextual conditions of each contextual factor. Each parameter measures the deviation from the standard rating as a result of the contextual condition.

The second model in [6] is called CAMF-CI, it assumes that each contextual condition influences the ratings for all items. This means that the effect of each contextual condition is different for all items. This model introduces a large number of parameters, for each contextual condition and item pair, a parameter is used to model the deviation of the rating. This model provides better prediction according to the authors in [6].

The third and last model is called CAMF-CC, it groups items into categories and assumes that the influence of each contextual condition is the same for each item category. A parameter is used to model the deviation for each contextual factor and item category pair [6].

A contextual condition in [6] refers to a value of a contextual factor; we further explain what it means later in this section.

The results of the experiments in [6] show that the CAMF-CC model performs better generally when compared to the other models in their work and another baseline context-aware factorization model. The problem with CAMF-CI is that it is too complex, thereby reducing prediction accuracy. One limitation of CAMF-CC when compared to our model is that it can only be used for items grouped into categories. CAMF-CC assumes that a domain expert can efficiently group items, this becomes a problem when items cannot be efficiently grouped. In contrary, our proposed methods group ratings based on the contextual conditions they occurred. For example, we group ratings of music played in the morning; morning here is a contextual condition of the time contextual factor. This doesn’t require a domain expert and makes the grouping and splitting process transparent. Another limitation of the methods in [6] is they capture only the influence of the contextual conditions on items. Our approach captures the influence of contextual conditions on users and items instead.

In [7], some correlation-based context-aware matrix factorization methods were developed and claimed to be an improvement over the models in [6], measuring correlation rather than rating deviation. The contextual correlation based CAMF measures the correlation between two contextual situations, the assumption is that two similar contextual situations for a user will produce similar recommendations for that same user.

The work in [8] proposed an “improved context-aware matrix factorization” that “fully” incorporates contextual information alongside with user and item biases. The authors claimed that other approaches do not fully capture the influence of contextual information on ratings. The authors developed two methods called ICAMF-I and ICAMF-II. Both methods compute and incorporate the user-context interaction and the item-context interaction into the models created. The first one (ICAMF-I), incorporates a global rating average, an item and user bias that aren't affected or influenced by the contextual factors.

The second method (ICAMF-II) built on the first method to incorporate item and user biases that changes over different contextual conditions. The item and user biases are modeled as the sum of all item and user bias over each contextual condition. Our methods measure and incorporate item and user biases for each contextual condition rather than as a sum. As an improvement to [8], we learn the item and user biases parameter for each contextual condition alongside the latent factors during training; this makes our contextual item and user biases more accurate and evolving as the rating behavior changes.

The authors in [9] created a context-aware recommender system that predicts the utility of items in a particular context. A tuple of user, items, context, and utility was used as the data structure to represent the problem of estimating the utility for a tuple. The utility of an item in a specified context is a function of its latent representation which is the column vector of the feature representation of the items and contextual factors. The Gaussian process was used to model the utility function.

• B.    Coupled Matrix Factorization

Coupled matrix factorization is an approach that performs a joint factorization of two or more matrices. Several attempts have been made to develop different variants of coupled matrix factorization methods in [10], [11] and [12]. However, our methods are the first and only context-aware coupled matrix factorization as far as we can tell. The work in [10] defines a coupled matrix factorization method that serves as the foundation of our proposed work. In [10] and [11], a coupled matrix factorization model was developed for factorizing two matrices by performing a joint matrix factorization of two matrices at the same time and minimizing using the gradient-based optimization method.

During the factorization of the two matrices, both matrices could share a common factor matrix. The idea for our work came from the common factor in [10]. However, we developed two models with two different variants of the common factor matrix in [10]. In our proposed methods, we use the term “common user factor” in our first model. The idea is that we assume a user’s taste remains consistent across different contextual conditions, but the item characteristics change in different contextual conditions. The second model assumes the characteristics of items remain the same over different contextual conditions but the user taste changes.

Another improvement we added to [10] is the addition of contextual user and item biases. The method in [10] doesn’t incorporate any bias. The reason for item and user bias is because, in the rating dataset, the rating dataset is affected by some users or items that have extremely high or low ratings. This doesn’t model the general opinion. We incorporate bias to neutralize these effects by accounting for the influence of those biases. Finally, we incorporate contextual information into our models, making our work the first and only context-aware coupled matrix factorization.

“Coupling” according to [12] and [11] means the relationship among attributes of items in a dataset. They created a coupled similarity method that measures the similarity between attributes and characteristics of items to identify the relationship in the dataset. They incorporated the coupled similarity method into the matrix factorization method to form a coupled item-based matrix factorization. We use the term “coupling” differently in our work; we use “coupling” to describe a process that jointly combines the factorization of different contextual matrices. We think our definition provides a better representation of the term “coupling” which means to combine or join.

Our proposed models add user and item biases which were not added in [12] and [11]. We do not compare our methods to the coupled matrix factorization methods discussed here because they do not incorporate contextual information.

• III.    Recommender Systems

Recommender systems are tools that suggest items to users. They are a special kind of information filtering system that predicts the rating or rank that a certain user would give to an item. A recommendation algorithm specifies how the system should perform the filtering of items; the algorithm predetermines how a user would rate or rank items. They typically take in a dataset containing the activities of users and extract the preferences of users, based on the historical data available in the system.

• A.    Collaborative Filtering (CF)

Collaborative filtering assumes that users who prefer similar items in the past will prefer similar items in the future. The function of collaborative filtering is to estimate the rating R over a set of users and items [13]. A collaborative filtering recommender system attempts to find users with similar ratings by comparing their historical behaviors; extracting similar users based on past behaviors and recommending items from similar user's catalogs.

CF model users with a matrix containing the ratings of items for each user. The models are used to extract factor vectors. These factors have different weights for each user and item factor models depending on the user’s profile. A CF system in contrast to a content-based system makes its recommendation based on the preference of similar users and not on similar properties of the items. CF assumes that ratings are directly proportional to preferences, thereby it places more weight and emphasis on the ratings given to the item by other users, rather than the characteristics of the item like content-based approaches does, even if the characteristics of the item matches what the user likes. In other words, CF in its pure form solely rates items based on its historical rating and completely ignores the characteristics of the items [14].

In the following sections, we discuss neighborhoodbased and model-based approaches.

• B.    Neighborhood-based Collaborative Filtering

Neighborhood-based recommender systems automate the word-of-mouth principle on which people rely heavily on what other people say, be it people they trust or people they share common opinions with [15]. The premise of the neighborhood method is that if users have preferred similar items in the past, the probability is very high that they will prefer similar items in the future, either on a user-to-user level or an item-to-item level. Some variations of neighborhood-based techniques compute item similarities and user similarities once and can make recommendations for users without having to re-compute similarities again; this makes it very scalable and fast.

The neighborhood-based methods are intuitive, simple to implement and it is easy to justify the results of their recommendations. One important thing for a recommender system is the explanation of how the recommended items were generated. This is important for transparency and trust.

• C.    Model-based Collaborative Filtering

Model-based methods create predictive models by learning and discovering features from the dataset. The created models are used to make predictions for the user. A model-based collaborative filtering method performs some offline analysis on the rating dataset to extract the models that represent the latent factors that describe the relationship and characteristics between the users and items. This model is loaded instead of the dataset during the recommendation process. When contrasted with the neighborhood and content-based recommender systems, a model-based system finds the distinctive features of users and items by taking a gander at the rating information. It builds the user profiles and items profiles with the end goal of reusing both entities for subsequent analyses.

As shown in Fig. 1, the utility matrix is the dataset representing users’ preferences. It is the structured dataset processed to discover the hidden features or factors for each user in the system.

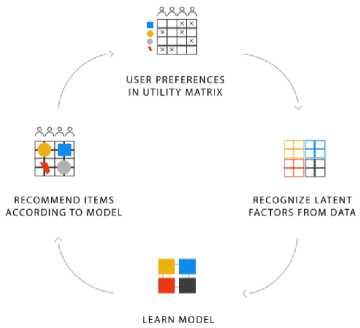
Fig.1. A framework for model-based recommender systems.

• IV.    Context-aware Recommender Systems

Many other factors could influence the preference of a user: a user may, for example, lean towards leisurely activities at the end of the week but goes for more business-related activities on weekdays. These factors can affect the preference of users in a great deal. Thus, it is vital to consider the appropriate context during the process of recommendation. It is stated in [16] that “contextual recommender system acknowledges the effect of context in the recommendation and that the preference for an item within one context can be different in another context. “ We use context and contextual information interchangeably throughout this section; they mean the same.

To understand the value of context in a recommender system, we describe the typical traditional recommender system and how context-aware recommender system extends it. Typically, a traditional recommender system uses two-dimensional data space to estimate the rating for items or users. The rating function R for a traditional recommender system is calculated for the (user, item) pairs that haven't been rated by the user and defined as:

• R: User x Item → Rating

Contextual recommender system extends the rating function by including one or more information in the form of context as shown below:

R: User × Item × Context → Rating

The context used by a context-aware and driven recommender system could be fully observable, partially-observable or unobservable contextual information. Fully observable context means that the recommender system has full knowledge of the structures and values of the contextual information relevant to the interaction between users and items. An example is a movie recommender system; the contextual factors might be time or location. The structure of the time context might be the days of the week, the month of the year, etc., and the structure of the location might be street, city, province, state, etc.

In the following sections, we discuss the context in a recommendation, ways of incorporating contextual information into recommender systems and some important components of a context-aware recommender system.

• A.    Context in Recommendation

According to [16], contextual information can be in a static or dynamic form. The static form is when the contextual information is the same over the lifetime of the recommender system. Dynamic form is when the contextual information changes over the lifetime of a recommender system. A function in the recommender system constantly detects the relevant contextual information and updates as required. Dynamic form conveys a notion of adaptability, the ability to adapt to changing contextual factors in the environment. The system detects the relevant context and updates recommendations during the user’s interaction with the system. This may occur in real-time where the context changes over time. Location is an example of a dynamic context that changes as you move from one point to another.

Contexts are factors that describe the environment and situations where the activity occurs. Much like rating data, we can acquire context data explicitly or implicitly. In the case of explicit context, the user needs to specify the context deliberately. For example, a user could specify additional information in the recommender system. This may not be dependable since it is easy for users to overlook some relevant activities, particularly when it involves a lot of contextual information and it is over a long period [17]. Implicit data is extracted automatically without user involvement when a user interacts with the system. An example is the collection of information like location coordinates, weather, user social activities, etc. Mobile phones have features like the global positioning system (GPS) to collect location coordinates and obtain weather information from weather services using the location obtained.

Representation of the contexts obtained follows after extracting or inferring the context. Using the approach in [5], we show an example of a contextual data representation for a location-aware recommender system below. We represent a context as a set of contextual dimensions, each dimension in the set is defined by a set of attributes having a variety of granularities [5].

Given a location recommender system, we represent the set of contextual dimensions as D containing toplevel contexts. D is defined below as:

D = { Place_Category, Weather}.

We further divide each element of D to a more granular or finer level such that:

Dpiace_category = {Food, Educational, Spiritual} and Dweather = {Winter, Summer, Fall}

• B.    Incorporating Contextual Information into A Recommender System

Unlike traditional recommender systems that solely rely on user preferences for some items, context-aware recommender systems use contextual information about the activities in addition to the user’s preferences. Incorporating context into a recommender system can be done in three ways: contextual pre-filtering, contextual post-filtering, and contextual modeling. Fig. 2, shows a general overview of the ways contextual information is incorporated into the recommendation process. The gray boxes represent the recommendation process in its pure form in sequence. The rating data goes into the predictions box, which represents the engine that performs the prediction and generates an output, the recommendations at the end of the process.

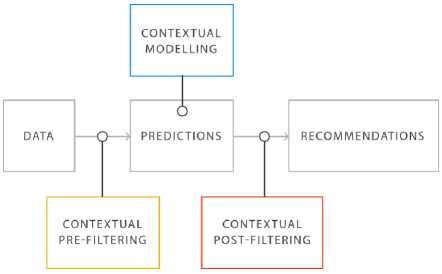
Fig.2. Incorporating contextual information in a recommender system.

Contextual Pre-filtering: filters the rating data using the specified context before the recommender framework computes the recommendations. Recommendations are computed by utilizing a subset of the data that are significant to the context. This approach uses contextual information to filter the dataset for the most relevant data (user, item, rating), before the process of recommendation [5]. A good example is a user that wants to find activities in a particular season; the recommender system only uses the preference data of the user and other users for that particular season.

Item Splitting is another pre-filtering approach. The concept is to split historical preference data that makes up the whole dataset profile into smaller segments and make predictions based a small segment. The major challenge of this approach is finding an efficient way to split the user profiles into optimal and appropriate segments [18]. This item splitting technique is referred to as micro-profiling. In [18], micro-profiling was applied on a music dataset to generate recommendations; the datasets were collected for a two-year period; it consists of implicit user feedback data, mainly the tracks the users of last.fm played. Multiple micro-profiles were used to model user’s profiles based on time cycles. The smaller profiles represented the user profile for a specific time context.

Contextual post-filtering: this approach applies the recommendation process on the whole dataset and after that uses contextual information to filter the results to get the contextualized recommendations. Post-filtering examines the preference of a user in a given context to understand the item usage pattern for the given context and applies it to adjust the recommendation list [5]. The recommendation list can be adjusted by either filtering out the irrelevant items for that context or by ranking the list based on relevance in the given context.

Post-filtering allows a traditional recommendation algorithm to be used in the process of recommendation before a filter is applied to select relevant recommendation. For example, in a location recommender system, if we want to recommend locations to a user based on a specific category, we filter and return only the locations in the specific category or rank the recommended results based on the category context.

Contextual modeling: incorporates context directly into its recommendation process. Contextual modeling uses a different approach to allow more than 2dimensional data to be utilized to make recommendations. The 2-dimensional data are the user and item. Contextual information can be incorporated directly into the recommendation process alongside the user and item data. Predictive models like context-aware matrix factorizations, regression and decision trees are examples of contextual modeling techniques that incorporate context into their approach.

The contextual modeling approach is divided into Heuristics and model-based methods. [19] described a contextual modeling approach called contextual neighbors that is based on collaborative user filtering. Heuristic-based methods extend traditional approaches. An example is the extension of the neighborhood approach using a multidimensional similarity method. The heuristic-based method finds the distance between users or items with similar context. The distance in consideration is the difference between the ratings being compared. To provide a generalized distance measurement, the dataset is grouped into segments using the available context, and the distance function is calculated on segments, this could help reduce sparsity where there are no adequate data for some contexts.

• V. The Proposed Methods

We propose two context-aware coupled factorization methods in this paper. The coupling part of our method is founded upon the approach in [10] which we explain in detail in this section. In section V.A, we provide a detailed explanation of our proposed context-aware coupled matrix factorization with common user factors. Section V.B provides a detailed explanation of our proposed context-aware coupled matrix factorization with common item factors. Section V.C details the addition of contextual user and item bias to our proposed methods.

• A.    Context-Aware Coupled Matrix Factorization with Common User Factors

In this section, we explain our proposed model called context-aware coupled matrix factorization with common user factors. We use the term “common user factors” because we make the contextual condition rating matrices to have the same user latent factors by compelling the user factor matrix of each contextual condition rating matrix to be the same.

The rationale for this approach is based on the assumption that to incorporate the effect of context, we assume that during user interaction, the effect of context on ratings reflects only on items. That is, across different contextual conditions, the taste of users remain the same while the suitability of items differs. An item might not be suitable in a context due to its characteristics. Since a rating is a weighted product of the user and item latent factor matrices, the changes in ratings are largely due to different values of item factors across the contextual conditions.

In this section, we define the objective function for our context-aware coupled matrix factorization with common user factor; this function is what computes the latent factors. The function generates the latent factors by minimizing the prediction error as shown later in this section.

Our method extends the approach in [10] by jointly factorizing R 11 , R₁₂ and R₁₃ , and sharing the same user factor matrix with all contextual condition matrices such that, R 11 ~ AB^T, R₁₂ ~ AC^T and R₁₃ ~ AD^T. A is the common user factor shared by the contextual condition matrices, where B, C and D are the latent item factors of the observed contextual condition rating matrices R 11 , R₁₂ and R₁₃ consecutively.

The objective of our method is to generate the latent factors and compute the mapping of users and items to factor matrices , B , C and D . Once we have done that, then we can predict ratings for users and items in a contextual condition, such that, R 11 = AB^T, R₁₂ = AC^T, and R₁₃ = AD^T . R 11 , R₁₂ and R₁₃ are the predicted ratings for each contextual condition. We do this by defining and solving a minimization problem that minimizes the prediction error to a local minimum. In the simplest form, the difference between the observed rating and the predicted rating called the prediction error denoted by e is defined in [20] (2) as:

e = R - R.                  (1)

Therefore, for each user-item-contextual condition rating pair, the prediction error in its simplest form is defined as:

^e uick     ^R uick     ^R uick ^{.              (2)}

Where R_uick represents the observed contextual conditional rating by user u for an item i in contextual condition ck . R_uick is the corresponding predicted or computed rating for a contextual condition rating by user и for an item i in contextual condition ck.

Building on (2), we define our proposed context-aware coupled matrix factorization with common user factors objective function that incorporates joint factorization as an extension of (1) of [10] as:

L = ||R11-(A x BT)|2 + ||R12 — (A x CT)|2 +

^R13-(A x DT)|2.

Where || || denotes the Frobenius norm for matrices used as a loss function, A is the common user factor matrix that contains the mapping of users to the latent factors, B , C and D are the latent item factors of R 11 , R₁₂ and R₁₃ containing the mapping of items to latent factors. The coupling can be seen here in the joint factorization process. The object function is solved as an optimization problem to minimize the prediction error while computing and learning the latent factors. This process generates our low latent factor matrices.

We modify our objective function in (3) by adding regularization to avoid overfitting during training, this generalizes the prediction rating model as much as possible to be able to predict unknown ratings. Regularization is done to penalize the magnitude of the low latent factors computed in the objective function.

We apply the constants a and /? as used in [21] and [22] to regularize the squared error on the set of the observed contextual condition ratings, this is defined below as:

L = |R11 -(Ax BT)|2 + |R12 -(A x CT)|2

+ |R13 -(Ax DT)|2

+ (/?HA| 2+ a|BH 2+ a HC| 2 + a HD| 2).

Where a controls the extent of regularization for the matrices B , C and D and /? controls the extent of regularization for the matrix A. a and /? are simply the penalty parameters.

To learn the latent factors in the low factor matrices, we optimize our objective function by solving the minimization problem below:

л;.  Нйц -(Л х ВГ)Н2 + №2 - (Л х

Л,О ,С ,U

CГ)H2 + HR13 - (Л х ОГ)Н2 + (/?НЛЦ 2 +

«НВН 2+ а HCH 2+ а НОН2).

We use the stochastic gradient descent approach in [21] and [23] to solve the minimization problem. The purpose of minimizing using the gradient approach is to achieve our objective of computing and learning the low latent factor matrices which contains the mappings to the latent factors.

The stochastic gradient descent method attempts to minimize the difference between the observed rating and the predicted rating iteratively until it finds the local minimum; then it terminates. Furthermore, we can break the minimization problem in (5) to:

. HR.ni -(Л. х ВГ)Н2 Ф|Г + |R13 -(Л. X D^W2 а\В£Н 2+ а ||С£Н 2+ а Ц^Ц

+ ^||R .i12 ^{- (Л} .

+ (^НЛ . Н ² +

х

Where Л . is the user vector factor for user u, В , is the item vector factor for item i in contextual condition 11, C , is item vector factor for item i in contextual condition 12 , D , is the item vector factor for item i in contextual condition 13.

Using the gradient descent method, we minimize the objective function during each iteration until we get to a local minimum. This process is used to learn our low factors. After completing this process, we obtain our low factors , B, C and D containing the mappings to the latent features.

The goals of this model are to generate the latent factors, compute the common user factors and contextual condition item factors of the observed rating matrix. After which we can predict the ratings for any user and item in any contextual condition. Predicting the rating of user u, for item i in a contextual condition would be a weighted sum of the common user factor vector and the corresponding item factor vector defined as:

f .ick = Л . 5 ^ . (7)

Where f_uick is the predicted rating of user u for item i in a contextual condition ck . Л . is the common user factor vector for user u and S( is the transpose of the associated item factor vector for item i in contextual condition ck, S could be B, C or D.

For two users to have similar ratings across different contextual condition, they must have similar common user factors and similar item ratings in a contextual condition. The core uniqueness of this method is generating common user factors for all the contextual condition rating matrices. All factor matrices contain the interaction/ mapping of users and items to the latent factors.

• B.    Context-Aware Coupled Matrix Factorization with Common Item Factors

In this section, we explain our proposed method called context-aware coupled matrix factorization with common item factors. We use the term “common item factors” because it forces the contextual condition rating matrices to have the same item latent factors by compelling the item factor matrix of each contextual condition rating matrix to be the same.

The rationale behind this approach is based on the assumption that to incorporate the effect of context; we assume that during user interaction, the effect of context on ratings is only reflected on users, the items maintain the same  characteristics  across  different  contextual conditions.  This means,  across  different contextual conditions,  the taste of  users  changes  while the characteristics of item remain the same. And since a rating is a weighted product of the user and item latent factor matrices, the changes in ratings is largely due to different values of user factors across the contextual conditions.

In this section, we show the changes in notation from section V.A; please refer to section V.A for the full description of the method. We define the objective function of our context-aware coupled matrix factorization with common item factor by building on the work in section V.A. In our proposed context-aware coupled matrix factorization with common item factor, we adjust the work done in section V.A by jointly factorizing R 11 , R₁₂ and R₁₃ , while forcing the matrices to share the same item factor matrix such that, R 11 ~ ВЛ^Т , R₁₂ ~ СЛ^Г and R₁₃ ~ DЛ^T . Л is the common item factor shared by the contextual condition matrices, where В, C and D are the latent user factors of the observed contextual condition rating matrices R 11 , R₁₂ and R₁₃ consecutively. We modify (4) to reflect the changes and define the objective function for this method as:

L = HR11 -(B X ЛГ)Н2+ HR12 —(C X ЛГ)Н2

+ HR13 -(D X ЛГ)Н2

+ (/?НЛН 2+ аНВН 2+ а HCH2 + а HDH 2).

Ultimately, we define our minimization task as:

л^,в |Rui11 — (В. X Л[)|2+ ||R.i12 -(C. X ЛГ)| + ||r13 - (d. x ЛГ)Н + (/^■'M 2 +

аЦВЛ 2 + а 11(7.11 2 + а HDJI 2).

Where Л , is the common item vector factor for item i, В . is the user vector factor for user u in contextual condition 11 , C . is the user vector factor for user u in contextual condition 12, D . is the user vector factor for user u in contextual condition 13.

Predicting the rating of user u for item i in a contextual condition would be a weighted sum of the common item factor vector and the corresponding user factor vector defined as:

fuick = s ^ a L (10)

Where f_uick is the predicted rating for user u, for item i in a contextual condition ck . A_i is the common item factor vector for item i and S_u is the associated user factor vector for user u in contextual condition ck , S could be В, C or D.

For two users to have similar ratings for a contextual condition, they must share similar user factor values for each contextual condition. They must also share similar item ratings within the context. The core uniqueness of this method is generating common item factors for all the contextual condition rating matrices.

• C.    Incorporating User and Item Biases in the Proposed Methods

To have a better and more accurate prediction of ratings, we incorporate user and item contextual condition bias into the objective functions of both our proposed methods. Biases are the variations in ratings due to individual effects certain users or items have. In a recommender system, there is a tendency for certain users to give higher ratings than others and for some items to receive higher ratings than others. This could be because some items or products are widely perceived as better due to factors like marketing, advertisement, etc. User bias and item bias captures the individual tendencies and variations. The item bias explains the tendency for an item to be rated lower or higher compared to the average rating and user bias explains the tendency for a user to rate higher or lower than the average rating.

User and item bias idea is gotten from the works in [21], [24] and [25]. The baseline estimate for an unknown rating that factors in item and user bias is defined in (1) of [21] as:

b_U i = ^+b i +b_u. (11)

Where b_ui is the baseline estimate for an unknown rating of item i by user u , ц is the mean, b_i is the deviation of item i from the mean and b_u is the deviation of user u from the mean. We propose item and user contextual factor bias to factor in the individual effects of users and items on the contextual condition rating calculation. We incorporate contextual condition item and user bias into the rating equations of (7) and (10) to produce:

• ^fuick = ^A u ^S i + ^ц ск + ^b ick + ^b uck ^{. (12)}

• ^fuick = ^S u ^A i + ^ц ск + ^b ick + ^b uck ^{. (13)}

Where цск represents the mean rating in the contextual condition ck, bick represents the bias of item i in the contextual condition ck, buck represents the bias of user u in the contextual condition ck.

The contextual condition biases for item i and user u for the three contextual conditions we have in our model are: ^b uii , ^b iii , ^b u12 , ^b i12 , ^b u13 , ^b i13 . Hence, we extend both objective functions and learn the biases in the minimization task and also regularized the biases to avoid over fitting, the extended functions of formulae (6) and (9) are

А,В,С,П,Ь_и11,Ь 111 ,Ь_и12,Ь 11 ₂,^^      ^HR “ ⁱⁱ¹ - (^A „ X ^ ) -

• ^ц 11 - ^b iii - ^b uii H² + H^ ui12 - ^(A u ^{X C}t) -^ц 12 - ^b i12 - ^b u12 ^^{2 +} 11^ 13 - ^(A u ^{X D}t) - ^ц 13 - b ii3 - b_u i3 H²+ ( Z?NA_uN ² + «HB i H ²+a HC i H ² + a HD t H ²+ a Hb tii H ²+ a Hb _un H ²+ a Hb ti2 H ² + a Hb_u i2 H ² + a Hb ti3 H ² + a НЬ_И 1з Н ²).

A,B,C,D,b_ull,b_h i ,b_ul2,^         H^_u^{ii1 - (B} _U ^{X Ai)-}

• ^ц 11 ^{- b} tii ^{- b} „ii H^{2 +} H^ ui12 - ^(C u ^{X A}D ^-ц 12 ^{- b} t12 ^{- b} u12 ^^{2 +} 11^ 13 - ^(D u ^{X A}I) ^{- ц} 13 - ^b i13 ^{— b} u13 H^{2 + (} /?H^A i H ^{2 + a}H^B u H ^{2 + a} H^C u H ^{2 +} a HD_UH ²+ a Hb tii H ²+a Hb _un H ²+ a Hb ti2 H ² + a Hb_u i2 H ² + a Hb ti3 H ² + a Hb_u i3 H ².

• VI. Evaluation

We test our recommendation methods by performing an offline experiment. Offline experiments are experiments conducted using datasets or data sources collected from user interaction with a system. We use implicit data; this means data collected about the activities of users which doesn’t explicitly show intent. We explain the characteristics of the last.fm music dataset used and after that discuss the evaluation criteria and methods used. Finally, we discuss the results, analysis and performance of our methods and chosen baseline methods in the test performed.

• A.    Dataset

In our experiment, we use the dataset obtained from the last.fm music website. The dataset contains the music listening history of users. For each user, the dataset contains the tracks played by the user and the timestamp the user listened to each track. Each track is represented by the track id, the title of the track, the artist id, and name. The dataset contains 992 users, 176,948 artists and a total of 19,121,228 listening entries. The last.fm dataset is an example of an implicit dataset.

The contextual factor in this dataset is time. We split time into three contextual conditions: morning, afternoon and evening/night. Morning represents the period between 12 am and 11:59 am, afternoon represents the period between 12 pm and 5:59 pm while evening/night represents the period between 6 pm and 11:59 pm. We group the dataset into three subsets, each representing the three contextual conditions. Each subset contains the listening history within the corresponding period.

We split this dataset into two, a training dataset and a test dataset. We use the training dataset to train our proposed methods. In the test dataset, we predict the artists a given user would like in a given period. We select artists from a set of new artists not in the user’s play history. We use the listening history data to get the play counts for an artist, in a given period. A user with a high play count for an artist in a given period, suggests that the user likes listening to that artist during that period.

• B.    Evaluation Method

To evaluate the performance of our proposed methods, we measure the prediction accuracy of our methods on our test dataset. We randomly select 100 users for testing. We divide our test dataset into three parts as explained in the dataset section, each containing user’s listening history for each time contextual condition, e.g., morning, evening, etc.

We evaluate the prediction accuracy of our methods on the test dataset using the Mean Absolute Error (MAE) and the Root Mean Square Error (RMSE). MAE is a popular statistical accuracy metric used in a recommender system to measure the deviation of a prediction or recommendation from the actual value [11]. MAE, as defined in (4) in [26], is defined below:

МАЕ = ^^и'‘| ^{Р и}'‘   ^Ти'¹ 1

N

P_Ui i is the predicted rating generated by our methods for user u and item i , r_ul is the actual rating (observed rating) for user и and item i in the test dataset. N is the total number of ratings in the test dataset.

RMSE is a popular metric for evaluating the accuracy of predicted ratings by measuring the deviation of a predicted rating from the actual value [27]. RMSE, compared to MAE penalizes large errors and prefers smaller errors. RMSE ,as defined in (4) in [26], is defined below:

RMSE = J 1 z_u ,i (P_u> i - r_u ,i )². (17)

P_ul is the predicted rating generated by our methods for user и and item i , r_{u l} is the actual rating (observed rating) for user и and item i in the test dataset. N is the total number of ratings in the test dataset.

We compare our methods with some baseline methods that incorporate context into their recommendation process.

The baseline methods we compare with our methods are:

• a.    Independent context similarity (ICS) and latent content similarity (LCS) methods of the correlation-based      context-aware      matrix

factorization (correlation-based CAMF) in [7]. We evaluate both ICS and LCS methods with the same training and test dataset used for our methods. The main rationale for choosing ICS and LCS is because they are both state-of-the-art context-aware matrix factorization methods, and they performed better than some existing context-aware matrix factorization methods according to the results of the experiment in [7]. Also, we needed methods that could generate recommendations for different contextual conditions instead of making general recommendations. A lot of the existing context-aware methods use context to make general recommendations. Another reason why we choose to compare our proposed methods with ICS and LCS is to demonstrate and confirm that incorporating changes in user behavior and item characteristics across contextual conditions as used in our proposed methods is more effective than generating recommendations based on the correlation between two contextual conditions used in ICS and LCS.

• b.    The context-aware matrix factorization (CAMF) methods in [6]. We compare our methods with CAMF-C and CAMF-CI in [6]. These methods are both state-of-the-art context-aware matrix factorization methods that can make recommendations for contextual conditions. We compare our proposed methods with CAMF-C and CAMF-CI to demonstrate and verify that our methods provide a better way to capture the influence of context on items.

• C.    Result and Analysis

We train our models using the training dataset to generate different latent factors with different dimensions (number of factors). After that, we conduct a series of experiments to evaluate the ability of our proposed methods to predict items for users in different contextual situations. We run different experiments to show the performance of our methods in comparison with the chosen baseline methods, using a different number of factors for each experiment. We provide the analysis of the results of the experiments conducted.

In running our experiments, we observed that, while the number of iteration is directly proportional to the effectiveness of our models, giving it a better MAE and RMSE scores, the number of iterations is also directly proportional to the time it takes to learn and generate our latent factors. The running time complexity of our methods is linear as a function of the number of iterations without taking the size of the dataset into consideration. Therefore, we use 10,000 iterations which took about 40 minutes to run an experiment on a 4 GB RAM machine.

In choosing our parameters a and /?, we did some try-and-error to arrive at the best values because calculating the appropriate values for these parameters has been proved to be a difficult research problem [28]. In our experiment, we measure the sensitivity of our model to each try-and-error value we set by measuring the MAE and RMSE at each step of the training. We observed that our models performed better with small values of both parameters. We settled for a = 0.6 and P = 0.4.

We run some experiments to measure the prediction accuracy of our proposed methods and compare them to the prediction accuracy of our chosen baseline methods using MAE and RMSE. We set the number of latent factors to different values for each experiment to test whether the number of latent factors extracted affects the prediction accuracy of the proposed methods and to compare the performance of the baseline methods to our proposed methods when different dimensions are extracted. We use 10, 20 and 30 as the dimensions of the latent factors and run different experiments for each dimension. We settled for these values after running different trials and observing that these dimensions provided the best prediction accuracies. The results are shown in Table 1. In the table, we will observe that setting the number of factors to 30 produced the best prediction accuracy.

We observe from our experiments that, context-aware coupled matrix factorization with common item factors shows better prediction accuracy for all dimensions, with an average improvement of 3.75% regarding MAE and 2.15% regarding RMSE across different dimensions. Context-aware coupled matrix factorization with common user factors show an average improvement of 2.75% regarding MAE and 1.43% regarding RMSE across the three dimensions used. Context-aware coupled matrix factorization with common item factors show an average performance of 25% and 20% regarding MAE and RMSE over context-aware coupled matrix factorization with common user factors. Therefore, we conclude that our proposed methods provide good prediction accuracy, but context-aware coupled matrix factorization with common item factors perform better than context-aware coupled matrix factorization with common user factors.

The characteristics of the music dataset used could be an explanation for why the coupled matrix factorization with common item factors performed better in our experiment. In a music recommender system, most tracks would normally have the same characteristics and suitability across different contextual situations. It is the changes in user’s taste in different conditions that account for what users consume in certain contexts. In certain scenarios where the changes in the consumption of items are largely due to the suitability of items across different situations, context-aware coupled matrix factorization with common user factor might perform better.

We run another set of experiments to compare our proposed methods to the selected baseline methods. Context-aware coupled matrix factorization with common item factors can average a performance improvement of 20.79%, 25.76%, 34.23%, 45.31%, in terms of MAE and 22.56%, 25.03%, 37.97%, 45.05% in terms of RMSE over correlation-based CAMF – ICS, correlation-based CAMF – LCS, CAMF-CI and CAMF-C respectively across different dimensions. Context-aware coupled matrix factorization with user factors also performs better regarding MAE and RMSE than correlation-based CAMF – ICS, correlation-based CAMF – LCS, CAMF-CI, and CAMF-C. We conclude that our proposed methods perform better than all the chosen baseline methods. The results are shown in Table 1.

The significance of using different dimensions for the latent factors is to investigate whether the number of the latent factors generated, affects the prediction accuracy of our proposed methods. Also, we wanted to see how the baseline methods compare to our proposed when we choose different dimensions for the generated latent factors.

Table 1. MAE and RMSE results of the experiment conducted

Method	No of latent factors / Dimensions	MAE	RMSE
Context-aware coupled matrix factorization with common user factors	10	0.545	0.772
	20	0.538	0.766
	30	0.530	0.761
Context-aware coupled matrix factorization with common item factors	10	0.479	0.698
	20	0.472	0.691
	30	0.461	0.683
Correlation-based CAMF - ICS	10	0.601	0.899
	20	0.591	0.890
	30	0.582	0.882
Correlation-based CAMF - LCS	10	0.644	0.927
	20	0.638	0.922
	30	0.621	0.911
CAMF-CI	10	0.752	1.152
	20	0.742	1.142
	30	0.701	1.101
CAMF-C	10	0.883	1.283
	20	0.852	1.252
	30	0.843	1.243

We observe that with a small number of dimensions used, our proposed methods can accurately capture the low latent factors needed to generate good predictions and as the number of dimensions increased to a certain extent (30 in our experiment), our proposed methods become more effective. From these experiments, the significance of using a different number of dimensions for the low factor matrices is to find the range of the dimensions that can effectively capture the latent factors that best describes the behaviors of users.

• VII.    Conclusion

In this age of big data and information explosion, providing recommendations help users to get relevant data in an online system. We aimed to develop a context-aware approach to making recommendations that are context centric; i.e., an approach that provides recommendations based on contextual rating, the rating given in a particular context. Therefore, our focus was to develop methods that provide recommendations for different contexts and not general recommendations.

After evaluating our methods on the last.fm dataset, our experimental results showed that both the proposed context-aware coupled matrix factorization methods showed a good performance on predicting new artists for users, but the method with the common item factor showed better prediction results. Therefore, the taste of users changes across different contexts, but the characteristics of items don’t change that much when compared to user’s behaviors, based on our experiments. This would make sense for certain items like music or artist; whether a user likes a song in the morning or evening is relative to the user for the most part. This means for two users to share similar artist taste in a context, they must have similar ratings or taste for the artist in the context being considered. Our results also show that other factors like parameters of the methods and number of iterations the method runs during the training affects the accuracy of prediction.

We compared our methods with some state-of-the-art context-aware recommendation methods, and our proposed methods showed a fairly significant improvement over all the methods considered. We have to mention that our method is more suited towards making predictions for specific contexts, and might be less effective in applying contextual information to make general predictions. Also splitting ratings into contextual groups before performing predictions make our method more effective towards performing context centric recommendations.

One limitation of our proposed methods are, they only incorporate one context. This would be a challenge in a domain or dataset with multiple contexts. Some scenarios would require the recommender systems to incorporate multiple contexts in its recommendation process. An example is an event recommender system with multiple contextual factors like time of the event, the location of the user and event, weather conditions, etc.

• VIII.    Future Work

Another interesting future work to consider would be, exploring techniques that adequately extract and share relevant user and item features across different contexts and contextual condition during prediction. We believe that although user behavior or item characteristics changes across different context, separating what changes from what remains the same across different context is very important to generate useful recommendations.

Another interesting further research would be how to make contextual predictions without manually identifying the contextual factors that affect users’ interaction and grouping the rating data by contextual conditions. One possible approach is to develop methods that could automate the process of identification and extraction of contextual factors. A possible way to do that is to examine the metadata and additional data that comes alongside the user-item rating for patterns and changes that correlate with the user-item rating data.