Control of an uncertain robot manipulator using an observation-based modified fuzzy sliding mode controller

Published Online March 2018 in MECS

The primary objective of this study was to design a robust nonlinear observer technique to improve the robustness of the fuzzy sliding mode controller for serial link robot manipulators. The mechanical architecture of the robot manipulators have complexities in that these systems behave nonlinearly with uncertainties in the parameters and couples. In addition, the dynamic parameters vary with time. Based on the robot manipulator’s structural properties, the design of a robust, stable, and reliable controller is significant for sensitive applications [1]. The control of robot arms can be divided into two broad categories, conventional control techniques and intelligent-based control methods. There are two main types of conventional control methods. The first type employs a linear-based control algorithm. This technique is used in several industries, but it cannot guarantee stability, robustness, and sensitivity.

The second type of conventional control methods utilizes a nonlinear model-based control algorithm. The most common nonlinear model-based controllers are the Computed Torque Controller (CTC), Sliding Mode Controller (SMC), back-stepping controller, and Lyapunov-based controller. Selecting a suitable control technique is a major challenge for many researchers [2-4].

The joint coupling effect is one of the significant factors to select the control technique for the robot manipulator. If linear controllers are candidates, there are two challenges to overcome with regard to the coupling effect: limitations of the velocity and acceleration of systems, and an increase of the gear ratio for linearization. As a result of these restrictions of linear controllers, we used nonlinear controllers in this paper. However, the Computed Torque Controller (CTC) can solve the problems of linear controllers, but it has three significant challenges: 1) extreme dynamic dependency on the system, 2) it requires an acceleration sensor, and 3) robustness. A sliding mode controller is the next candidate to solve the challenge of the coupling effect concerning system performance. Apart from several advantages, this method contains the problem of high-frequency system oscillation (chattering) and limited robustness [3-7]. Adaptive techniques have been used to solve the challenge of robustness [8-12].

A fuzzy sliding mode controller is proposed to solve the robustness challenge in a sliding mode controller. Apart from several advantages in particular conditions, this method contains the problem of chattering in uncertainty. A proposed observer is used to modify the fuzzy sliding mode controller by applying a sliding mode observer to reduce the chattering and improve the robustness. This methodology improves the performance of the conventional sliding mode and fuzzy sliding mode theory in the presence of uncertainty concerning the model reference and stable observation technique. The rest of this paper is organized as follows. The second part outlines the related works. The third part focuses on the problem statements. In the fourth part, the proposed observation-based fuzzy sliding mode controller are presented. In the fifth part, we analyzed the proposed method. In the final section, we provide conclusions.

• II.    Related Works

Robot manipulators have been extensively used in industrial to replace humans or for many other complex specialized applications. These complex specialized applications require robots with nonlinear mechanical architectures, which create multiple challenges for modeling and control in various systems. To solve this challenge sliding mode control algorithm have been introduce by researchers [2-3]. Apart from several advantages, conventional sliding mode controller contains the following problems: chattering phenomenon and limited robustness [3-5].

To solve the challenge of chattering, two methods introduced by researchers: functional-based method and intelligent-based method [6-7]. A functional-based linear boundary layer algorithm, has been developed by Slotine [6]. Apart from numerus positive points to reduce the chattering, this method increases the error and reduce the robustness. To reduce the chattering and error as well, Palm has been developed intelligent-based boundary layer method [7]. However, this method has been solved the challenge of error and chattering as well, but the problem of robustness and tuning the fuzzy coefficients were still remaining. To solve these challenges adaptive technique is introduced [8-12].

A nonlinear adaptive observation method based on the adaptive multiplicative algorithm, which is a sensitive decision procedure for the uncertain linear time-varying system, has been developed by Nikolay Karabutov [8]. The challenges of identification, estimation, and observation of the parametric uncertain (PU) linear system were presented by Nikolay Karabutov [9]. The model referencing an adaptive sliding mode controller for an uncertain system dynamic fault tolerant was given by Xiao et al . [10]. In this paper, the observer section compensates the control part in the presence of system uncertainties and actuator faults. The chattering free super-twisting sliding mode controller for the robot manipulator in the presence of uncertainties and external disturbances has been presented by Goel and Swarup [11]. To remove the chattering, they proposed a homogeneous sliding manifold and super-twisting sliding mode controller (STC). Xu [12] presented a chattering free adaptive sliding mode controller for the motion control of a piezoelectric nano positioning stage in the presence of uncertainty and disturbance estimation. To eliminate the chattering, he proposed a discontinuous stable control term.

• III.    Problem Statements

A robot manipulator is a multi-DOF link. This system is highly nonlinear and possesses a multi-input multioutput (MIMO), coupling effect, and uncertainty of the dynamic parameters. This system is used in many applications and is forced to work in unknown and unstructured conditions. The dynamic formulations of the robot manipulator are considered in the equation shown below.

^{т - T} d = I ⁽ q )[ ^{q ]}+ V ⁽ q , q ) + G ⁽ q )          ⁽¹)

In (1), if V ( q , q ) = B [ qq ] + C [2, to model this system, the dynamic equation can be arranged as follows.

• [ q ] = I ^{- 1}( q ).{ t - [ V ( q , q ) + G ( q ) + T d ]           (2)

A ( q , (q ) = I ^{- 1}( q )[ t - t ] represents the uncertainty for modeling in a robot manipulator.

According to (2) and the role of uncertainty, the following relationship can be obtained.

[ i| ] =A( q , q ) - 1 ^{- 1}( q ).[ V ( q , q ) + G ( q )]          (3)

Based on (3), in the first step to address the challenge of the coupling effect in the robot manipulator, a sliding mode controller is presented in this paper. In the second phase, a defined and limited uncertainty condition fuzzy logic controller is applied to the sliding mode controller to address the chattering. In the third part, a model reference sliding mode observer is introduced to improve the stability, robustness, and accuracy in the fuzzy-based sliding mode controller. The bounds of the uncertainty are modeled as follows.

1 1 "*( q )[ t — T_d ] = A( q , q )

Table 1 shows the list of the robot manipulator’s dynamic equation abbreviations.

• IV.    Proposed Methodology

Solve the coupling effect:

Reducing the coupling effect is the first objective in this paper, and the sliding mode controller is the best candidate. This control algorithm has two main sections: 1) a function-based part and 2) a model-reference section. The first part is used to improve the stability and robustness in the sliding mode technique. Different functions have been proposed by researchers, but the best function to improve the stability and robustness is a highspeed switching mode function. The function-based SMC is defined as follows:

[ U F ] = K F × f ( s )                  (5)

where UF,KF, f(s) , and s are the functional model-free controller, function coefficient, linear or nonlinear function to improve the rate of stability and robustness, and sliding surface, respectively. The sliding surface is divided into two main categories, linear and nonlinear. The nonlinear sliding surface algorithm is used to improve the performance of the sliding mode controller.

Table 1. Dynamic information of the robot manipulator

I	Time varying inertial matrix	n × n
5 [ qqA	Time varying Coriolis matrix	n × ( n - 1) n × 2
C [ q ] 2	Time varying centripetal matrix	n × n
G	Time varying gravity vector	n × 1
τ	Torque vector	n × 1
q , q , q	Position, velocity, and acceleration vector	n × 1
τ d	Disturbance of load vector	n × 1
V ( q , ci)	Nonlinear robot manipulator term
A ( q , i?)	Modeling the disturbance
∆	Bound of uncertainty

[ 5 ( x , t )] = Я х ^ ( e , e , £ e )           (6)

According to the Lyapunov stability theorem, the stability of this controller is proved as follows:

V = XT.M.X(9)

where V is the candidate Lyapunov stability function, X is the variable state, and M is a state of the stability term. To have a stable system, the following must be true.

V>0→M>0

The derivation of the Lyapunov stability function is proposed as follows.

V = XT. Ml. X + XTMX(11)

According to (7) and (11), MX based on the sliding surface is obtained as shown below.

MX ''('У I (q) = -1 "*( q )V (q, q) I( q)

- 1 ^{- 1} ( q ) G ( q ) I ( q ) -Ф ( q , q r)

Based on (11) and (12), derivation of the Lyapunov stability function can be calculated as follows.

In (6), X , v , e , e , ^ e

are the sliding surface slope,

linear/nonlinear method used to define the optimal surface, error, change of error, and integral of error, respectively. The reach time and chattering phenomenon are two important factors in the design of the sliding surface. These two factors are contradictory in that a fast response output experiences the chattering phenomenon. One of the objectives of this paper is to outline a quick response controller. Uncertainty is a significant challenge to design the equivalent section of a sliding mode controller. The functional-based section is used to

.          T •         A 1       A           *

V ? = X T ( MX - 1 ^{- 1} ( q ) V ( q , q ) I ( q )

- 1 ^{- 1} ( q ) G ( q ) I ( q ) -Ф ( q , ))

Considering (8) and (13), the algorithm of the Lyapunov derivation is calculated as follows.

V ? = X T ( MX -1-\q ) V ( q , q ) I ( q )

- 1 ^{- 1}( q ) G ( q ) I ( q ) + Ф( q , q ))

estimate the equivalent part in a sliding mode controller. The equivalent part of the SMC is obtained as follows:

[U m ] = I"4 q )V ( q , q ) I ( q ) + Г*( q ) G ( q ) I( q )

+ ^fs ) I ( q ) + Ф( q , q ) + T

∂ t

where ф ( q , q ), i_r are the effect of the system’s uncertainty and the time to reach the trajectory, respectively. Considering (5) and (7), the Lagrange formulation of SMC can be formulated as follows.

[ U SMC ] = [ U F ] + [ U M ] = K F × f ( s ) + Г\ q ) V ( q , q ) I ( q ) + Г^г( q ) G ( q ) I ( q ) + ^{f ( S )}- I ( q ) + Ф ( q , q ) + T.

∂ t

Based on the Lemma equation, the limitation of stability is obtained as shown below.

K u = [| MIX I + - V ( q , q ) - G ( q )| ±Ф ( q , ) + n ]        ⁽¹⁵⁾

Therefore, the stability is shown below.

v ? <-jh n X. ф              (16)

i = 1

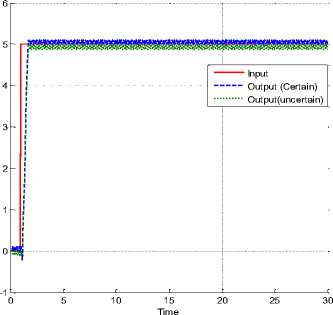
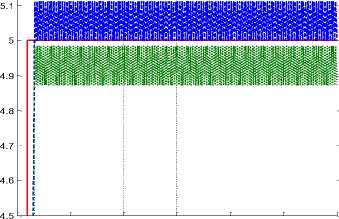
Fig.1 shows the output trajectory following in the conventional sliding mode.

5.3

5.2

Input

Output (Certain)

Output(uncertain)

[ S ( x , t )] M = [ 2 x ^ ( e , e , £ e )] + [Ax ф ( e , e ? )]       ⁽1⁷⁾

Input

Output(Certain)

Output(Uncertain)

0         5         10        15        20        25        30

Time

Fig.1. Joint tracking accuracy of the SMC in certain and uncertain states

0         5        10        15        20        25        30

Time

4.9

4.8

Input

Output(Certain)

Output(Uncertain)

Based on Fig. 1, the output position has chattering and the rise-time is about 1.1 second. Considering the results shown in Fig. 1 and the sliding mode controller equations, the traditional sliding mode controller for the robot manipulator has chattering. This problem causes heating, losses of energy, and instability in the robot manipulator. Based on the results, the level of chattering in the certain and uncertain situations is about 20%.

4.7

4.6

0         5         10        15        20        25        30

Time

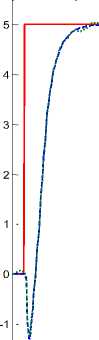
Fig.2. Joint tracking accuracy of the BL-SMC in certain and uncertain states

Solve the chattering problem: The main idea to reduce chattering is to evaluate the sliding mode function, which has been improved by researchers over the years. The first technique was a linear boundary layer function. The linear boundary layer was introduced to solve the challenge of chattering. However, while this theory is used to reduce chattering, proving the stability is impossible. Figure 2 shows the output tracking performance in a linear functional-based SMC. Based on Fig. 2, the linear boundary layer function reduces the chattering in certain situations, but it remains a great challenge in the presence of uncertainty and disturbances. Based on the results, the rate of error and the rise-time increase in the presence of uncertainty and disturbance. The rise-time increases from 1.1 seconds to 2.6 seconds. From a control point of view, the challenge of proving stability is fundamental. In the proposed method, to solve this issue, a linear-based theory is presented in parallel with a high-speed switching function. The proposed method to eliminate the chattering is obtained as follows:

where [ S ( x , t )]_м, ф ( e , e) are a modified sliding surface function and a PD-based function, respectively. This method reduces the rate of chattering and preserves the stability in the SMC.

U f ] m = K f x f ( S m )             (18)

According to (8) and (18), the chattering free sliding mode controller is obtained as follows.

^[U SMC ^] M = ^{[ U} F ^] M ^{+[ U} M ^] = ^K F ^{x f ( S} M ^{) +}

ГЧ q ) V > ( q , q .) I ( q ) + Г\ q ) ( 5 ( q ) I ( q )

+ df(SM) |( q) + Ф( q, q) + Tr dt

However, according to (19), ф ( _e , e) causes a reduction of chattering but it has a challenge of robustness. Fig. 3 shows the joint tracking in the modified SMC.

Time

5.2

Input

Output(Certain)

Output(Uncertain)

5.15

5.1

5.05

4.95

4.9

4.85

4.8

4.75

4.7

0          5         10         15         20         25         30

Time

Input

Output(Certain)

Output(Uncertain)

∑ µ ( x ). x ω ( x ) = ⁱ

∑ µ ( x )

i

Here, µ ( x ) is the degree of membership in the fuzzy-based theory.

U u^ ] PD = ^«1 e , e) + У r4 e , У e )    (22)

According to (7) and (22), the following relationships can be derived.

У( q )V ( q , q ) I ( q ) + Г\ q ) G ( q ) I ( q )

+fs) I ( q )+Ф( q , q ) =                <23>

У /4 e,e) + У /4 e, У e )

U ,m ] M = I "*( q )V ( q , q ) К q )+ 1 "*( q ) G ( q ) I ( q )

f I ( q )+Ф( q , q ) +                   (24)

У fd^ e , e¹) + У 7 T ® ⁽ e , У e )

The robustness is modified based on (24). To prove the stability, the following equations can be utilized.

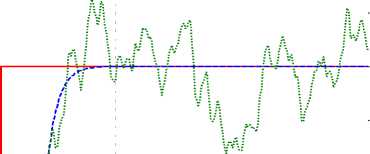
Fig.3. Joint tracking accuracy of the modified SMC function in certain and uncertain states

Based on the comparison of Fig. 2 and Fig. 3, the performance of the proposed method in certain and uncertain situations is significantly better. As shown in Fig. 3, the proposed function eliminated the chattering and reduced the rise-time from 2.6 seconds in the linear boundary layer SMC to 1 second. Nevertheless, this method solves the challenge of chattering in a certain state, but cannot guarantee steady state error convergence in uncertain conditions. There are two major factors which must be considered to address this challenge. The first one is dependence on the system dynamic and the second is robustness.

Solve the challenge of dynamic dependency: To solve the first issue, a modified fuzzy sliding mode is presented. In this case, the fuzzy algorithm is recommended to estimate the system behavior in the presence of disturbance and uncertainty. The main idea of this method is defined as follows:

[ U Fuzzy ] = ∑ ₁ ^K γ ^T ω ( x )                (20)

where γ ^T and ω ( x ) are the tuner coefficient factor and the primary function of the fuzzy-based system, respectively, which is defined by the following equation.

MX = ejXs^tjX I ( q ) = - 1 -i₍ q V ( q , q ) j ( q ) ∂ t

^- I ^{- 1 (} q ) ^{G (} q ) I ⁽ q )^-ф( q , q ) - У / T ® ⁽ e , e ? , У e )

If :^ф( q , <7) + У ^Y X^e,^e, У e ) = ^ ⁽ и )

MX = ^{d f} ( s ( ^t )) I ( q ) = - 1 -1₍ q )V ( q , q ) I ( q ) ∂ t

- I ^{- 1}( q ) G ( q ) I ( q ) - ζ ( u )

The derivative can be obtained as shown below.

r-J

V ? = X T ( MX -1 ^{- 1}( q ) V ( q , ) I ( q )

- I ^{~ - 1}( q ) G ^~( q ) I ^~( q ) + ζ ( u ))

The Lyapunov stability function is defined by (28).

n v? <-Уn1xz i=1

Figure 4 illustrates joint tracking for the proposed fuzzy sliding mode controller. A comparison of Fig. 3 and Fig. 4 reveals that the performance of the modifying fuzzy sliding mode technique is better than that of the proposed sliding mode controller. This method also improves the rise-time from 1 second in the proposed

SMC to 0.8 seconds in the modifying proposed SMC. To solve the issue of robustness, the observer-based fuzzy proposed SMC is presented. In the state space, if x_i = q and X 2 = q , the Lagrange formulation of the robot manipulator is defined as follows [13-15].

X = x_: - ,X _!,( i = i,2,3,....)

w ( X i , X 2 ,~ 2 ) = f ( X i , x 2 ) - f ( X i, . X 2 )

The system and control uncertainties are defined as shown below.

X j = x₂ = q

^X 2 = q = ^{f (} x i , x 2 ) ^{+A (} q , ^{q )}                     (29)

y = xi where, f (X, x 2) = I -i( q )[^ (q, q) + G (q)]

Pe = A ( x_x , x₂ ) + Z ( u )          (32)

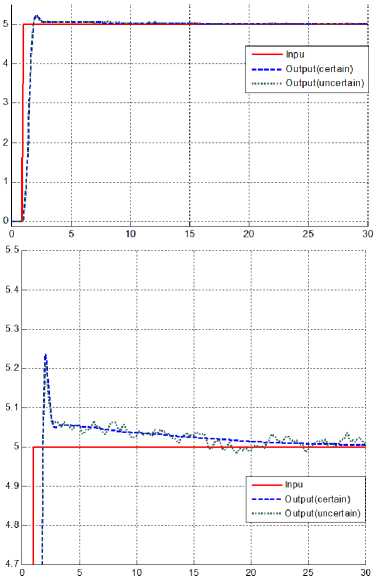
Fig.4. Joint tracking accuracy of the PD+PID fuzzy-based SMC in certain and uncertain states

F = w ( x , x₂ ) + ^{d f ( S} ) jT( q ) + Pe + ^{i 2Z}      d t

У f rn⁽ e , e ? ) + У У rn⁽ e , У e ) = ^f h

Fig. 5 shows the joint tracking accuracy in certain and uncertain states for the sliding mode observer fuzzy sliding mode controller.

4.5

3.5

2.5

1.5

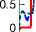
5.02

5.01

Based on (23), the state space function is obtained as follows.

Inpu output (Certain) Output (Uncertain)

10          15          20          25          30

4.99

4.98

4.97

4.96

0           5          10          15

Inpu output (Certain) Output (Uncertain)

20         25         30

X 1 = XL 2 + K_$ x f ( s )

О                df ( s )    _x , x           (30)

^X 2 = ^{f (} X i , X 2 )⁺ ^² I ⁽ q )⁺ S ⁽ S m ) +       ⁽ )

У / ^ i e , ^{e )} + У / ^ i e , У e )

According to (29) and (30), the state estimation error is calculated as follows.

J X i = X~ 2 + K f x f ( s m )

X 2 = w ⁽ x i , x 2 )^{+d f} ( S ) ^I( q )⁺ s ^{( s} m )^+A( q , q ')^{+     (3i)}

^ /^( e , e ? ) + £ /^( e , y e e )

where

Fig.5. Joint tracking accuracy of the model-reference observer modified fuzzy-based SMC (certain and uncertain)

As demonstrated in Fig. 5, the model reference observer sliding mode technique removed the fluctuations, overshoot, and chattering under certain and uncertain conditions. Therefore, this method solved the challenge of robustness in the proposed fuzzy SMC. Based on this method, the error convergence is close to zero. From comparing the results shown in Fig. 5 with the previous figures, it is seen that the proposed method solves the two main challenges of chattering and robustness.

• V.    Results and Discussion

To examine the power of robustness and eliminate the chattering, the sliding mode observer fuzzy sliding mode controller and proposed fuzzy sliding mode controller were analyzed and applied to an industrial (PUMA) robot manipulator. In the first step, the trajectory following accuracy for these two approaches was compared. Fig. 6 shows the comparison between these two methods. Based on Fig. 6, the modified fuzzy SMC has about 5% overshoot and error.

Desired Output

Proposed Method

Modified Fuzzy SMC

Desired Output

Proposed Method

Modified Fuzzy SMC

5         10         15         20         25         30

Time

-1

10         15         20

Time

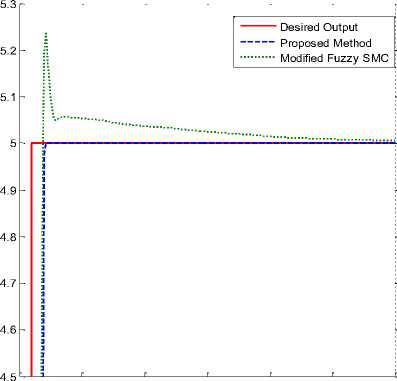
Fig.6. Position tracking accuracy of the model-reference observer modified fuzzy-based SMC and modified fuzzy SMC in the certain state

10         15         20

Time

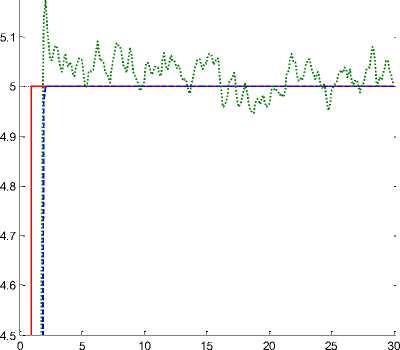
Based on the results shown in Fig. 6, from a robustness point of view, the proposed model reference observer fuzzy SMC is much more robust than the proposed fuzzy SMC. These two methods have the same rise-time. The rate of error convergence in the proposed model reference observer method is near zero. The power of robustness for the proposed model reference observer fuzzy SMC method and proposed fuzzy SMC is compared in Fig. 7. As seen in Fig. 7, the observation-based theory improved the robustness in the presence of uncertainty and disturbances. These two methods have the same rise-time in certain and uncertain conditions. The RMS error in the proposed method is lower than 2 x lO ^{- 4}, whereas it is 0.015 in the modified fuzzy-based SMC.

5.3

5.2

Desired Output

Proposed Method

Modified Fuzzy SMC

Time

Fig.7. Position tracking accuracy of the model-reference observer modified fuzzy-based SMC and modified fuzzy SMC in the uncertain state

0.09

0.08

0.07

0.06

0.05

0.04

0.03

0.02

0.01

Proposed Method

Modified Fuzzy SMC

0          5         10         15         20         25         30

Time

-0.01

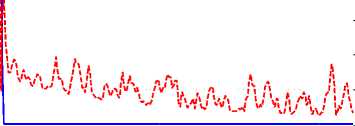
Fig.8. RMS error in the model-reference observer modified fuzzy-based SMC and modified fuzzy SMC in the uncertain state

Lastly, the RMS errors of these two approaches are compared in Fig. 8. Based on the results, the observerbased method removed fluctuations and the error convergence is near zero. The modified fuzzy SMC has variation in the uncertainty condition. These results prove the power of disturbance rejection and the robustness of the proposed observer method as well.

• VI.    Conclusion

This study proposes a technique to solve two significant challenges. The first challenge is the coupling effect in a robot manipulator. To address this challenge, the robust sliding mode was recommended. Although this method has positive attributes, chattering and robustness remain challenges. A fuzzy sliding mode controller is presented. This approach eliminates the chattering and improves the rise-time in the certain state, but it cannot guarantee stability in the uncertainty state. To solve this problem, the model reference sliding mode observer was recommended. The robustness is the principal positive point of this method. In this method, the rate of RMS error in certain and uncertain conditions is near zero, the rate of chattering phenomenon is near zero in the certain and uncertain conditions, and remarkably, the rate of fluctuation in this observation control theory is zero.

Acknowledgment