Coriolis Force and centrifugal force in electrodynamics and mechanics

Modern ideas about the Coriolis force [1] are as follows:

• •    Coriolis force is in no way associated with any interaction of the body in question with other bodies,

• •    Coriolis force is determined by the choice of a specific non-inertial reference system.

• •    Coriolis force is not physical strength and does not do work.

Roughly speaking, the Coriolis force acting on a body appears because another body rotates at a certain speed next to this body. Our body does not interact with this body and therefore "does not know" the magnitude of this speed, but the Coriolis force depends on this speed. The mass of this other body and the distance to it does not matter. Coriolis force doesn't do the job but

• •    a freely falling body deviates,

• •    rails of one-way railways wear out unevenly,

• •    long-range artillery shells deviate from the calculated trajectory, etc.

So,

• •    there is an inertial reference system rotating with the angular velocity vector <5,

• •    there is a non-inertial reference system that does not interact with the non-inertial reference system,

• •    in a non-inertial system, a body of mass m moves at a speed V ,

• •    in this case, the Coriolis force acting on the body perpendicular to

the velocity V is observed, which is determined by the formula

FK = — 2m(< x V).                               (0)

This force is observed as fictitious from a non-inertial reference frame, as, for example, in the experiment with the Foucault pendulum. But the same force is also observed from the inertial reference system, such as, for example, the real destructive force of a riverbank. Observation can be carried out even from the third system , in which the non-inertial reference system rotates, in which the inertial reference system is located, as in the experiment [5]. In this case, we observe how in a non-inertial system a fictitious force physically draws a spiral ... Therefore, the Coriolis force cannot be considered fictitious and explained by the features of observer perceptions.

Fig. 1.

It is necessary to try to find the physical connection of a real rotating system with a body moving in or near this system.

2.    Interaction of moving electric charges

Let's consider fig. 2, where at points A and B two charges q 1 and q₂ are shown, moving with speeds V 1 and v₂ , respectively. It is known that the magnetic induction of the field created by the charge q₂ at the point where the charge q 1 is currently located is

В = q2(v2 x r)/r3.

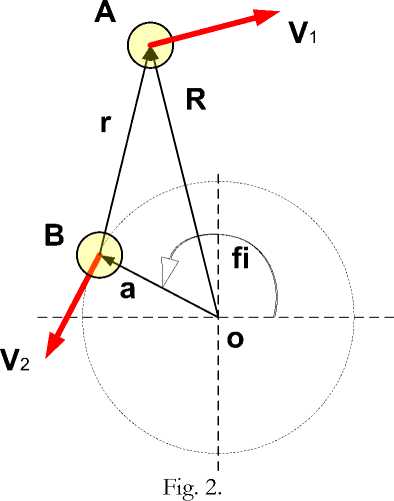
In this case, the vector r is directed from the point where the moving charge q 1 is located. Lorentz force acting on the charge q 1 ,

^12 = qiOh x В).

or

^12 = qiq2(v1 x (v2_x r))^3).

In fig. 2 also shows the vectors a and R, and the vector a makes the angle ( with the horizontal axis ox and r = R -a.(4)

First, we consider the case when all these vectors lie in the horizontal plane oy, and we denote the projections of all vectors by the subscript coordinate. Then the vector

W = (V 2 x r) = z(v 2 Xry - V 2 yrx),	(5)
where z is the unit vector of the vertical axis. Denote W z = (V 2x r y - V 2y r x ).	(6)
Then w = zwz.	(7)
If the charge q2 rotates around point O with an angular velocity CO , then
the vector r 2 = coaexp (i ; )	(8)
is tangent to a circle with radius a . Wherein W z = ca (cos (p + ^ )r y - sin (p + ^ ) r x )	(9)
or wz = —ca(sin(p)ry + cos(p)rx).	(10)
From (3, 5) we get: F 12 = q i q 2 (r 1 x W)/(r3)	(11)
or, taking into account (7, 10), F 12 = q i q 2c o(v 1 x z^)/(r3) .	(12)

Suppose now that q₂ is the density of charges located uniformly on the entire horizontal plane, and this plane rotates with an angular velocity CO around point O. Moreover, the linear velocity v₂ of each point is determined by (8).

We find the force acting from such a charged and rotating plane on the charge q i

—

F =

J F₁₂ dpda =

J (q^c (r i x z

^/(r3)) dpda

p,a                 p,a или

F = q i Q 2 (r 1 x coW), where

co = zco ,

W = J ^^dpda.

J p,a r3

From (15, 10) we find:

w = -J” a (J0271(sin(p)ry + cos(p)rx)r-3 dp) da, where r is determined by (4):

rx = Rx - acos(p), ry = Ry — asin(p), ax = acos(p), ay = asin(p).

Integration according to these formulas gives a remarkable result: the value of W does not depend on R and, as the upper limit tends to от , approaches to

W ~ —45.

Therefore, formula (13) can be written as

F = qiq2W(v1 x O),

You can notice an analogy between the formulas for the force (20) and for the Coriolis force.

3.    The interaction of a rotating electric charge with a motionless field of electric charges

We now consider the electric charge q_; , which rotates above the field of electric charges. Coulomb forces from the side of a rotating charge should rotate the field of electric charges. In this case, the problem reduces to the previous one: indeed, the charge q_; moves above the rotating field of electric charges. For the identity of these problems, we must also assume that the field of charges does not have its own rotation or the speed of this rotation is significantly less than the speed of rotation of the charge q_; . Thus, in this case too, we can use the formula (20). The linear velocity V 1 of the charge q_; and its angular velocity CO are related by the formula

• V1 = Ro,                                   (20a)

3.    Maxwell's equations for gravitomagnetism and Coriolis force

where R is the radius of rotation of the charge q_; . Combining (20, 20a) we find:

F = q_;q₂WRo² .                          (20b)

One can notice an analogy between the formulas for force (20b) and for centrifugal force.

In [2], the author proposes a new solution of Maxwell's equations for gravitomagnetism, which is used to construct mathematical models of various natural phenomena (sand vortex, sea currents, whirlpool, funnel, water soliton, water and sand tsunami, turbulent flows, additional (nonNewtonian) interaction forces celestial bodies). All of these models use the concept of mass currents as flows of particles of mass. The velocity of mass particles can be very small and often their flux can be invisible as well as the flux of electrons. But the existence of these phenomena and the possibility of constructing the indicated mathematical models similar to mathematical models of direct current in electrodynamics [4] confirm the assumption of the existence of mass currents and the interaction of mass particles, which is completely analogous to the interaction of electric charges.

Based on this, it can be assumed that the rotation of the body is accompanied by a mass current, similar to how the rotation of a charged body is accompanied by convection electric current. Eichenwald [3] showed that such a current creates magnetic induction. Based on the complete analogy between the Maxwell equations for electrodynamics and gravitomagnetism [2], it can be argued that when the body rotates, gravitomagnetic induction is created. A mass m moving in a gravimagnetic field with speed V is affected by the gravitomagnetic Lorentz force (an analog of the Lorentz magnetic force).

Based on the foregoing, we rewrite formula (20) obtained above for the interaction of electric charges, as applied to the interaction of mass charges:

F = Wpm(V x o) ,                            (21)

where m, V are mass and speed of a moving body,

W « -45, p is the surface density of masses as elements of mass current,

О is the angular velocity of rotation of the plane on which these elements are evenly distributed.

Comparing formulas (0, 21), we find that

-2 = Wp,(22)

whence it follows that mass density p = --« 0.044= 4.4 • lO-5-^.

r W         m2              sm2' '

“Let me,” - the attentive reader will be surprised. “Do you reject the Coriolis theory and at the same time use its formula?” I can only join in his surprise and be even more surprised that such different methods of reasoning led to the same formulaic result! Nevertheless, the conclusion of the mass density (23) can be accepted only if there is a reliable experimental verification of the coefficient “2” in the formula (0) of the Coriolis force.

The used method of deriving the Coriolis force proves the reality, not the fictitiousness of this force, and discovers the source of power for this force - the Earth's gravitational field.

5.    Centrifugal force

As shown in section 3, the rotation of a charged plane under a moving charge can be replaced by the rotation of a charge above a charged plane-Then in formula (20) ) is the vector of the angular velocity of a rotating charge, the linear velocity of this charge

V1 = Rb).(24)

When applying formula (20b) to the interaction of mass charges, we obtain

F = Wpm

This formula is different from the centrifugal force formula

Fc = m)2R, only by a coefficient. By analogy with the previous one, we find the mass density p = - A « 0.022   = 2.2 • 10-5 -m^.

r W         m2              sm2k

Thus, the nature of the centrifugal force is the same as the nature of the Coriolis force, and the source of power for this force is the Earth's gravitational field