Correction of the arc array excitation using genetic algorithm

The circular arc phased arrays as part of cylindrical arrays widely used for navigation radio beacons. This is due to the possibility of wide-angle scanning (360°) of the summary and difference patterns, which has practically permanent shapes on azimuth plane. The arc array differs from linear and plane array the lesser level of mutual coupling between array radiators. In this case the axes of the radiators located above cylindrical surface mutually unfolded from each other.

The general scanning mode for arc array is switching moving (step-scanning) of the fixed arc array (fixed number of the radiators and fixed amplitude and phase distribution) on the cylinder perimeter for given discrete scan angle Aa 1 , which equal the angle interval between radiators. More accurate subscanning mode for angle discrete Aa 2 = Аа 1 Пп , where n is an integer, is made for fixed arc array due to using digitally controlled discrete phase shifters. An amplitude distribution also is fixed.

Such subscanning mode necessary to implement with minimal distortions for given angle sector Aa 1 . In fact, minimal phase discrete АФ limits the accuracy of the bearing direction of difference pattern and direction of the maximum for summarize pattern. The arc array far-field pattern can be approximated by [1]:

N

F ( ф ) = E I n ,0 frad ( ф ^- ф n ) exp { [ ^kRc ^cos ( ф^- ф n ) ^- V n ,0 ] } ^{,                                    (1)}

n = 1

where N is an integer number of the radiators; I _{n 0} , v _n 0 is amplitude and phase of the n -th radiator; k = 2n]X is wave number of the medium; X is wavelength of the electromagnetic field; R_c is radius of the circular array. The pattern of radiator in Eq. (1) often define as ideal pattern of the single radiator, located above the infinity perfectly conducting plane screen, that is: f rad ( ф - ф _n ) = cos ( ф - ф _n ) .

To improve the accuracy of alignment phase distribution for subscanning mode we use exact electromagnetic equations. These equations are used to determine both the mutual coupling of the array radiators and influence of the current distribution on cylindrical surface.

For the array radiators as the vertical dipoles are located above an extensive cylindrical surface we use an asymptotic correspondence of 3D vector and 2D scalar electromagnetic problems [2]. Thus, we

Краткие сообщения

have the filaments of electrical currents as 2D radiators are located at the dipoles coordinates and parallel them. The amplitude and phase distribution these dipoles are equal to I n ,0 , у _n ,0 , n = 1: N , the limit radius of the filaments is a << X . Assuming a perfectly conducting cylindrical surface, the boundary conditions for the tangential components of the total electric field leads to system of the summarize-integral equations:

2              N2

J jSH0 (krpq ) dlq + E In,1H0 (krpq ) = - EIn,0H0 (krpq ); P 6 Lc; n=1

Lc(2)

N

J j_S ^H 0² ) ( kr pq ) dl q + I m ,1 H 0² ) ( ka ) + E I n ,1 ^H 0^{2 }} ( kr pq ) = ⁰ P ^€ P m ; m = ^1: N , n ^ m

Lc where In,1 is the current induced on n -th array’s radiator; In,0 is an excitation current; js is the current on the contour Lc as the section of cylindrical surface, formed by perpendicular plane to the axis z .

Thus, the total pattern of the arc array as solution of exact Eq. (2) defined by: ^N

E z ( ф ) = E ( I n ,0 + I n ,1 ) H 0^{2 )} ( kr pq ) + J j_sH 0² ) ( kr pq ) dl q ,                                          (3)

n=1                                  Lc we assume that axis z is parallel to the filaments.

The serious problem for numerical solution of the Eq. (2) is large size of the discrete form as system of the linear algebraic equations, especially for large dimensions of cylinder contour. We use the numerical approach for decreasing such size as two stage procedure. First: we solve the Eq. (2) for given L_c that has large, but limited R_c , acceptable for using computer recourses. Second: we introduce new limited arc L_a to substitute for contour L_c . Then we obtain numerical solution of the Eq. (2) for given arc L_a . Comparing of two patterns from Eq. (3) for these cases shows that limited arc L_a for angle 130° is perfectly enough for practically using accuracy. Fig. 1 depicts comparing exact pattern for contour L_c , exact pattern for arc L a and approximate pattern from Eq. (1). In this case X = 0.32 m, R_c = 2.2 m, and optimal amplitude and phase distribution I _{n ,0} . We use projective method of the collocations for numerical solution of the Eq. (2), using high-accuracy Gauss quadrature formulas.

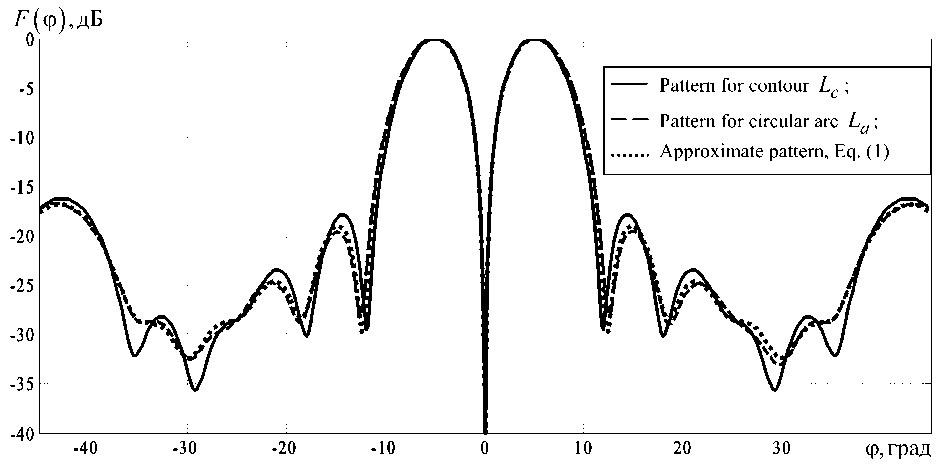
Fig. 1. Difference patterns of the circular arc array in azimuth plane

Thus, using limited arc L_a as part of the contour L_c can reduce time computation of the Eq. (2) almost three times with sufficient accuracy of results. High-speed computations and reducing of the computer recourses is necessary to use effective optimization techniques for synthesis of an arc array patterns.

We consider some examples of synthesis the correct phase distributions for given subscanning mode is including angle sector ±2.5° and step-scan 0.5° for fixed arc array. For comparison we use wide-known quasi-Newton technique [4] and actively developing genetic algorithm [5].

Genetic algorithm includes the following steps.

• 1.    Creating the set of genotypes of the initial population – it means creating the set of random vectors of phase distribution v П0 , P = 1, q, these vectors are divisible to minimal phase discrete АФ =11.25°, q is dimension of the set.

• 2.    Evaluation of the genotypes set using adaptation function, it means defining of the aim functions ^ p ( v П ,о ) , p = 1, q •

• 3.    Selection of the most adapted population, which correspond to the minimal value of the aim function.

• 4.    Check of the convergence criterions (the number of iterations, no decrease the values of the best aim function for some step by step iterations). Then, if at least one of the criterions is done, it necessary to remember the best vector, else go to 5.

• 5.    Mutation, it means adding some random numbers vector d to all components of vector v _n 0 • This vector correspond to minimal value of the aim function. Besides, random numbers are divisible to minimal phase discrete АФ . The purpose of such mutation is creating new vector set, rather adaptive for optimization criterions.

• 6.    Go to 2.

Fig. 2 depicts the result of the synthesis the correct phase distributions for two patterns of the arc array, these patterns are correspond subscane mode angles Ф 1 = - 2.5 ° and ф ₂ = 2.5 °.

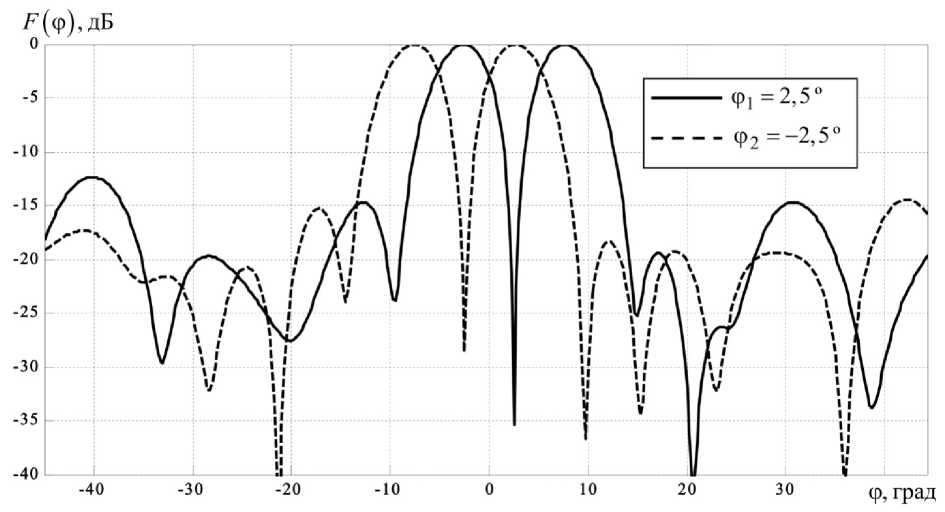
Fig. 2. Difference patterns of the circular arc array in subscane mode

Evaluation of the bearing direction accuracy shows that azimuth errors does not exceed the value 0.23 % for all the set of subscane mode given directions. In terms of the bearing direction accuracy the genetic algorithm and the quasi-Newton method give out almost identical results. However, the ge-

Краткие сообщения

netic algorithm is based on variation of the random vectors, therefore the computation time is variable and it can be obtained as average time for computation the set of given iterations. Then, comparison of these synthesis approaches shows, that using the quasi-Newton method requires more then 1.53 computation time to obtain similar results.

Thus, the genetic algorithm has some numerical advantages over other practically used optimization techniques, especially for large-scale problems. The defects of the genetic algorithm are fuzzy criterions for optimization procedure return, considerable dependence of the solution stability and convergence on size the random vectors.