Correlations between elements and sequences in a numerical prism

We obtained the numerical set { U ( n ; k , j ) } structured as a «numerical prism» in the paper [1]. The construction of the numerical prism is based on relations between the cumulants χ_n and the initial moments a_n , where n e N , of the hyperbolic-cosine-type probability distribution defined [2, 3] by the characteristic function:

- m f (t) = | ch—t - i—sh—1| , where ц,р,ш e R; m > 0, в * 0, i = V—1.              (1)

V — в m )

The obtained three-parameter distribution is described in [4] and is a generalization of the Meixner two-parameter distribution [5].

Theorem 1 ([1]). For a hyperbolic-cosine-type distribution with the characteristic function (1), the formula for calculating the cumulants x_n , n = 1,2,..., is the following:

n              nn

Xn = mв  Pn ^ I = mШ £V(n;j) ^ I ,(2)

V m )   < в ) V m ) j=0

where P_n ( b ) are polynomials of the form:

n

Pn(b) = ZV(n;j)bj, n = 1,2,...,(3)

j = 0

and the coefficients V ( n ; j ) of the polynomials are calculated by the recurrence relation:

V (1;1) = 1, V (1; j ) = 0 for all j * 1,

V ( n + 1; j) = ( j - 1) V ( n ; j - 1) + ( j + 1) V ( n ; j + 1) for n e N .               (4)

The polynomials P_n ( b ) follow differentiation of the tangent function, and are known [6, 7] as Derivative polynomials .

Theorem 2 ([1]). For a hyperbolic-cosine-type distribution with the characteristic function (1), the formula for calculating the n -th order moments is the following:

n

M ( X ) = a n = И! P n V m J

( m ’1

V ^e

( |

V m J

T V _; ( n ; k.j ) m k k = 1 j = 0

j

^ | , n = 0,1’2, V p J

where the moment-forming polynomials of two arguments P_n ( m , b ), n = 0,1,2,..., can be represented in the form:

nn

^P n ⁽ m ’ b ) = ZZ ^{U ( n} ; ^k ’ j ) m k b j ’                               ⁽⁶⁾

k = 1 j = 0

b = ^в , { U ( n ; k , j ) } is a system of the integer coefficients of the polynomials related by the equations: U (0; 0,0) = 1, U (0; k , j ) = 0 for any k , j * 0,

U ( n + 1; k , j ) = U ( n ; k - 1, j - 1) + ( j - 1) U ( n ; k , j - 1) + ( j + 1) U ( n ; k , j + 1),        (7)

for n = 0,1,2,....

The identity U ( n ; 1, j ) = V ( n ; j ) follows directly from equations (4) and (7). Therefore, the numbers V ( n ; j ) are only special cases of numbers U ( n ; k , j ) for k = 1.

For each fixed k , where k e N , the corresponding subset of { U ( n ; k , j ) } forms a numerical triangle. In terms of geometry, the set { U ( n ; k , j ) } is a set of numerical triangles ordered by k , and can be considered as a «numerical prism», where for each given k the triangle is a section of the prism [1, 8]. Similarly, we can obtain sections of the prism by fixing the argument j , j = 0,1,2,.... These sets are usually novel.

Let us either fix two of the parameters n , k , j , or express two of them through the remaining parameter. The numerical sequences obtained in the numerical prism include many well-known sequences (tangent numbers, secant numbers, Stirling numbers of the first kind, coefficients in expansions of various functions, for example, in the Bessel polynomials, etc.) [9]. However, the overwhelming majority of the obtained sequences is not mentioned in the literature. The issue of novelty is solved with the help of a sufficiently complete on-line encyclopedia of integer sequences ( OEIS ) [10].

We notice the lasting interest in numerical sequences and triangles. For example, the paper [11] presents a numerical pyramid which sections are known numerical sets: those of Deleham, Euler, MacMahon, Stirling. Also, the paper [11] gives a series of numerical sequences, among which only the sequences A 000182, A 000184, A 00147, and A 085734 in OEIS are common with the numerical prism. Other sequences and triangles are also present as subsets in the considered numerical prism. The paper [12] identifies the first elements of the numerical triangle { U ( n ;1, j ) } as the numbers T_n k calculated by the recurrence relation T_nk = 5 1 _k , T_{n + 1 k} = ( k - 1) T n _k - 1 + ( k + 1) T n _{k + 1}. This is a special case of relation (7). Along with interest in finding new numerical sequences, there is an increasing interest in classical sets of numbers considered from different points of view. In particular, the paper [13] presents simple and asymptotically fast algorithms for calculating tangent and secant numbers. In the considered numerical prism, we can not only easily calculate these sequences, but also establish structural relations between the sequences.

Cumulants and moments in the numerical prism structure

Therefore, the considered numerical prism is an ordered set { U ( n ; k , j ) } of the coefficients of the polynomials P_n ( b ) and P_n ( m , b ) that form, respectively, the cumulants and moments of the hyperbolic-cosine-type probability distribution [1]. Moreover, according to (2) and in view of the equality

Математика

U ( n ; 1, j ) = V ( n ; j ), the distribution cumulants are completely determined by the distribution parameters p.,P,m and the set of coefficients { U ( n ;1, j ) } :

( R An   ( и A ( в A n "         ( и A j ( в A n "             .-

Xn = m I —I Pn -I = m I —I £ V (n; j) 4| = m I — I £ U (n ;1, j) bJ , where b = -.(8)

V m J l в) V m) j=0      l в) V m) j=0

For n = 1,12, j = 0,10, the corresponding section { U ( n ;1, j ) } is partially presented in table 1. According to (7), subsequent values are calculated simply, without using differential relations. Note that the section { U ( n ;1, j ) } is the known [10: А 008293] triangle of coefficients in the expansion of tg ^{( n} ) x in powers of tg x .

Table 1

Section { U ( n ;1, j ) } of the numerical prism

n	0	1	2	3	4	5	6	7	8	9	10
1		1
2	1		1
3		2		2
4	2		8		6
5		16		40		24
6	16		136		240		120
7		272		1232		1680		720
8	272		3968		12096		13440		5040
9		7936		56320		129024		120960		40320
10	7936		176896		814080		1491840		1209600		362880
11		353792		3610112		12207360		18627840		13305600
12	353792		11184128		71867136		191431680		250145280		159667200

In order to calculate the initial moments α_n of the hyperbolic-cosine-type distribution (see (5)), we use the parameters u>P>^m along with all sections of the numerical prism { U ( n ; k , j ) } determined by k , where k = 1, n .

Let us consider the relation between the moments and cumulants with reference to the set { U ( n ; k , j ) } .

As is well known, the moments { a n } and cumulants { x s } of probability distributions are connected by the following polynomial relations:

^a 1 = X i ;

a 2 = X 2 + x 2 ;

a g = X з + 3 X 1 X 2 + X 1³ ;

a 4 = x 4 + (3 X 2 + 4 Х 1 X 3 ) + 6 X 12 X 2 + X 4 ;                             (9)

« 5 = X 5 + (5 X 1 X 4 + 10 X 2 X 3 ) + (10 X 12 X 3 + 15 X 1 X 2² ) + 10 X 3 X 2 + X 15 ;

^a 6 = X 6 + ⁽⁶ X 1 X 5 + ¹⁵ % 2 % 4 + ¹⁰ X 3²⁾ + ⁽¹⁵ X 1² X 4 + ⁶⁰ X 1 X 2 X 3 + ¹⁵ x 2 )

+ ⁽²⁰ X 3 X 3 ^{+ 45} X 1² X 2^{2) + 1} 5 X 4 X 2 ⁺ X 6 ;

……………………………………………………………………………. .

In the above expressions, the terms are grouped according to the number of cumulants-factors in the product. For any n , n e N , the relation takes the form:

n                                        s1 ,s2 ,...,sk s1 s2       sk k=1 S1+ s 2+...+Sk=n,

S i ^ 0

where k is the number of the multiplied cumulants, as1,s2,...,sk are the corresponding coefficients at the products χs1 χs2 ...χsk , and si is the order of the cumulant χsi .

Theorem 3. For the hyperbolic-cosine-type distribution, consider the decomposition of the initial moments a n into sum (10) of the cumulant products with given coefficients. Then the number of cumu-lants-factors in the corresponding terms is determined by the parameter k in the formula:

nn n an = F| E mk E U (n; k, j) bj . V m ) k=1 j=0

Proof. As it follows from (5), (10), nn n                        n an = FI EEU(n;k,j)mkbj= E E     «м2, v m ) k=1 j=0                         k=1 S1+s2 +...+Sk = n,

...

., s_k ^χ s ₁ ^χ s ₂ ... ^χ s_k .

s , * 0

According to (8), the cumulants considered in (12) can be represented as:

( в A

X s, = m FI E U ⁽ s i ;1, j ) b .

i I m ⁾ j = 0

Note that, regardless of the order s_i of the cumulant, there is a factor m in equation (13). quently, there is a factor m ^k in each product of k cumulants, despite of different orders s ₁, s ₂,

Conse-

...

, s_k of

the cumulants χ χ ...χ . s1 s2

Substitute the cumulants in the form of (13) into the right side of (12):

( R An n n              , n                            k ( nVisi an = (в) EEU(n;k-j)mkbj = E    E    a,,2 s,П (в) mEU(si;1,j)b

V m ) k=1 j=0                        k=1 S1+s 2 +...+Sk = n,             i=1 _v m )

s i * 0

i.e.

« n

n _{n n}                          n _n

( - ) E m ^k E U ( n ; k , j ) b j = F) E m k E a s , s₂

V ^m )   k = 1     j = 0                     V ^m )   k = 1      s _{1 +} s ₂ + ... + s_k = n ,    ¹ 2

s , * 0

, s_k П E ^U ( s , ;^1,j ) b i = 1 l j = 0

, (14)

where each term of the polynomials of variables m and b on the right side of (14) is such that the pa-rameter k of m ^k indicates the number of cumulants-factors in the corresponding product. Since the polynomials on both sides of (14) are equal, coefficients at the same powers of m are also equal. Then, the following equality holds for any m :

nn m FI EU(n;k,j)bj v m ) j=0

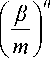
mk E

s 1 + s 2 + ... + s_k = n , s i * 0

s ₁, s ₂

., s _k П E ^U ( s i ; ^1, j ) ^b j i = 1 L j = 0

Therefore,

v^) j=0                    s1+ s 2 +...+sk = n, si *0

At the same time, the power k and number of cumulants in the product are equal for each term on the right side of the equation.

This completes the proof of Theorem 3.

Theorem 4. There are the following relations for coefficients of the polynomials P _n ( m , b ) :

J i,

E U ⁽ n ; k , ^j ) ^b j = E      ^a s 1 , s 2 ,..., s_k П E ^{U ( s} i ;1, ^j ) b

, where k = 1, n .

j = 0                        s j + s 2 + ... + s_k = n ,                i = 1 _l j = 0

s i * 0

Proof. Divide both sides of (15) by ( в/m ) n and compare expressions of the same powers of m in the polynomials.

Математика

Corollary 4.1. For any b , the following condition holds for the section { U ( n ;2, j ) } of the numerical

prism:

n                                                s                                I

УU(n;2, j)b = У as,l  У U(s;1, js)bj ■ У U(l;1, jt)bj j=0                   s+1=n,       Ljs=0                 J Ljl =0

s , I * 0

In particular, compare coefficients of the same powers of b in the polynomials and obtain:

U(n;2,j) = У asl   У s+1=n,       Ljs+ji=j s, I *0

U ( s ;1, j s ) ■ U ( l ;1, j l ) , where j = 0, n .

Corollary 4.2. For any b , the following condition holds for the section { U ( n ;3, j ) } of the numerical

prism:

Уu (n ;3, j) bj j=0

= У  ars, l i+s+1=n, i, s, l *0

i                                s

У U ( i ;1, j i ) b j   У U ( s ;1, j_s ) b j^s

. j = 0              JL j s = 0

У u ( l ;1, jl ) b j j l = 0

In particular, compare coefficients of the same powers of b in the polynomials and obtain:

U(n;3,j) = У  ai,sj     У i+s+1=n,         L j- + js + jl = j i, s, l *0

U ( i ; 1, j i ) ■ U ( s ; 1, j s ) ■ U ( l ; 1, j_t ) , where j = 0, n .

Corollary 4.3. If b = 1, then relation (16) implies the following relation for coefficients of the polynomials P_n ( m , b ) :

У u ( n ; k j j = 0

У    %- 2

s i + s 2 + ... + s k = n , s , * 0

k     s i

, s k П У U ( s ;1, j, ) i = 1 L j- = 0

, where k = 1, n .

Corollary 4.4. If b = 0, then relation (16) implyies the following relation for coefficients of the polynomials Pn(m, b) :

k

^{U ( n} ; ^k ,0) =      У       ^a s 1 , s ₂,..., s_k П ^{U ( s} i ; ^1,0) , ^{where k} = 1, ⁿ .

s1+s 2 +...+sk = n, s, *0

In particular,

U ( n ;1,0) = У a s 1 U ( s 1 ;1,0) = U ( n ;1,0) ; s i = n ,

U(n;2,0) = У as,l U(s;1,0)U(l;1,0);(23)

s + 1 = n , s , l * 0

U(n;3,0) = У   ai,s,l U(i;1,0)■ U(s;1,0)■ U(l;1,0).(24)

i + s + 1 = n , i , s , l * 0

Corollary 4.5. If b = 0, then the following relation is obtained from (22) by summation over k : nnk

У U (n; k ,0) = У У     as1, s 2,..., sk П U ( s,;1,0).(25)

k=1                   k=1 si+ s 2 +...+sk=n, si *0

Theorem 5. In a section of the numerical prism { U ( n ; k , j ) } , the numerical triangle { U (2 n ; k ,0) } is a decomposition of the secant numbers { E_n } into the sum of products grouped by the number of factors of the tangent numbers { T n } . Namely,

n

^E 0 = 1, E n = Z Z             a 2 s 1 ,2s 2 ,...,2 s_k T s₁ "  T s ₂ "  ... " T s k ,                      ⁽²⁶⁾

k = 1 2 s i + 2 s 2 + ... + 2 s k = 2 n ,

S i * 0

where n e N , a _{2 s} 1 _{2 s} 2 ₂ s k are the positive integer coefficients in the representation, see (9), of the initial probability moments a _{2 n} = E n as the sum of products of the cumulants X 1 , X ₂,—, X _2n (2 s ₁, 2 s ₂,..., 2 s_k are even orders of the multiplied cumulants).

Proof . According to [8], if the parameters of the hyperbolic-cosine-type distribution are ц = 0, в = 1, m = 1, then the cumulants { x _{2 n} } are tangent numbers x 2 _n = T n , n e N , and the initial moments { a _{2 n} } are secant numbers: E ₀ = 1, a _{2 n} = E n , for n e N. In addition, for ц = 0, в = 1, m = 1, relation (13) implies that:

X2n = U(2n; 1, 0), x2n-1 = U(2n -U,0) = 0;(27)

and relation (11) implies that:

2 n2 a2n = Z U(2n; k, 0), a2n-1 = Z U(2n -1; k,0) = 0, k=1

since U (2 n - 1; k , 0) = 0 for n , k e N .

We use relation (25) only for even n and s_i (since U ( n ; k , 0) and U ( s_i ; 1, 0) are equal to zero, if n and s_i are odd). Redesignate the indices and obtain:

2n                  2nk

Z U (2 n ; k ,0) = Z Z       a 2 s 1 ,2 s 2 ,...,2 s k П U (2 ^,0).

k=1                     k=1 2 s1+2 s 2 +...+2 sk =2 n, si *0

For nonzero summation indices, if 2s1 + 2s2 +... + 2sk = 2n, i.e. s1 + s2 +... + sk = n , then k < n . Consequently, in the equality above, the summation over k is conducted from 1 ton . Therefore, nnk

Z U (2 n; k ,0) = Z Z       a 2 s1,2 s 2,...,2sk П u (2 s;1,0), k=1                     k=1 2 s1+2 s 2 +...+2 sk =2 n, si *0

i. e.

a2n = Z       Z       a2s,.2s22skПx2si ■(28)

k=1 2 s1+2 s 2+...+2 sk=2 n, si *0

Replace the moments and cumulants by the corresponding secant and tangent numbers a _{2 n} = E_n , x _{2 s} i = T s i in (28). We arrive at relation (26):

n

E n = Z Z              a 2 s 1 ,2 s 2 ,...,2 s k T s 1 "  T s 2 " ... " T s k .

k=1 2 s1 +2 s 2 +...+2 sk =2 n, si *0

This completes the proof of Theorem 5.

Theorem 6. For fixed k , k = 1,2,...,2 n , each of sequences { U (2 n ; k ,0) } is a sequence of such terms in the decomposition of secant numbers { E_n } that contain k factors consisting of tangent numbers. Namely,

U (2 n ; k ,0) =         Z             a 2 s 1 ,2 s 2 ,...,2 s k T s 1 "  T s 2 " ... " T s k ,                      (29)

2 s 1 + 2 s 2 + ... + 2 s k = 2 n , s i * 0

n

E n = Z U (2 n ; k ,0),                                 (30)

k = 1

where { T_i } are tangent numbers, a _{2 s 1 ,2 s 2 ,...,2 s k} are positive integer coefficients in the representation, see (9), of the initial moments a _{2 n} = E_n as the sum of products of the cumulants X 1 , X ₂,..., X _2n .

Математика

Proof . In order to obtain equation (29), replace n by 2 n in (22) and use relation (27), where x 2 _s = T s i • Relation (30) follows from (26) and (29).

Corollary 6.1. The sequence { U (2 n ; 1,0) } is a sequence of the tangent numbers { T n } .

The statement directly follows from (29), since 2 s 1 + 2 s ₂ + ... + 2 s ^ = 2 n , a _{2 s} 1 _{2 s} 2 ₂ s k = a _{2 n} for k = 1, and all coefficients a _{2 n} of the highest cumulants % _2n in formulas (9) are equal to 1.

Corollary 6.2. The sequence { U (2 n ;2,0) } satisfies the following relation:

U (2 n ;2,0) = £    a 2 s ,2 l U (2 s ;1,0) U (2 l ;1,0) =    £    a 2 s ,2 l T s ■ T l .

2 s + 2 1 = 2 n ,                                         2 s + 2 1 = 2 n ,

• s ,    I * 0                                                        s , I * 0

The statement is a special case of (29) and (23), since T_s = x _{2 s} = U (2 s ; 1, 0) for any s , s e N .

Corollary 6.3. The sequence { U (2 n ;3,0) } satisfies the following relation:

U (2 n ;3,0) =     £      a 2_t,2 s ,2 _z U (2 i ;1,0) ■ U (2 s ;1,0) ■ U (2 l ;1,0) =     £      a 2,,2 s ,2 _z T_t- T s ■ T l .

2 i + 2 s + 2 l = 2 n ,                                                             2 i + 2 s + 2 l = 2 n ,

• i ,    s , l * 0                                                                                          i , s , l * 0

The statement is a special case of (29) and (24), since T_s = x _{2 s} = U (2 s ; 1, 0) for any s , s e N .

Using the formulas for representation of cumulants in terms of moments, we can also obtain inverse relations expressing the tangent numbers { T } in terms of the secant numbers { E_n } indicated in the section { U ( n ; k ,0) } .

By analogy with Theorems 5 and 6, we can also represent relations between other sequences. Let us give two examples. Let ц = 1, в = 1, m = 1. Then cumulants and moments of distribution connected by mutually inverse relations are the sequence (1, 2, 4, 16, 80, 512, 3904, 34816, …) [10: А 000831] and the sequence (1, 1, 3, 11, 57, 361, 2763, 24611, …) [10: А 001586], respectively. The latter sequence is given by generalized Euler numbers. For ц = 1, в = 1, m = 2 , a sequence of cumulants, i.e. a sequence of alternating secant and tangent numbers, and a sequence of moments are equal up to a shift on two positions: x_k = a_{k - 2}, k = 2,3,... [8]. Therefore, this sequence can be restored by the previous elements (autoexpression). If we know the structure (representation of cumulants through moments and, conversely, moments through cumulants), then we can use the numerical prism to find specific terms in the expression of each sequence through its pair sequence.

Remark 1. For 2 n <  12, if all moments and cumulants of odd order are equal to zero, then the coefficients a _{2 s 1 ,2 s 2 ,...,2 s k} used in the formulas to connect moments and cumulants of even order are as follows:

^a 2 = X 2 ;

^a 4 = X 4 ^{+ (3} X 2 );

« 6 = X 6 + (15 X 2 X 4 ) + (15 x 2 );                                (31)

« 8 = X 8 + (28 X 2 X 6 + 35 X 42 ) + (210 X 2 X 4 ) + (105 X 4 );

« 10 = X 10 + (45 X 2 X 8 + 210 X 4 X 6 ) + (630 X 2 X 6 + 1575 X 2 X 4² ) + (3150 X 3 X 4 ) + (945 X 5 );

« 12 = X 12 ^{+ (66} X 2 X 10 ^{+ 462} X 2 ⁺ 495 X 4 X 8 ) ^{+ (1485} X 2 X 8 ^{+ 13860} X 2 X 4 X 6 ^{+ 5775} X 3^{) +} + (13860 XX 6 + 51975 X 22 X ) + (51975 X 4 X 4 ) + (10395 X 2⁶ );

Remark 2. In order to illustrate the theory, the fragment of section { U ( n ; k ,0) } of the numerical prism is given in table 2 (initial values for n = 1,16, k = 1, 8 ). The rows present terms in the expansion of secant numbers by tangent numbers.

Conclusion

In the present work, the structured values of the numerical prism result in different relations and regularities in the field of numbers. At the same time, the numerical set {U(n; k, j)} has other applica- tions. For example, for given coefficients {U(n;k, j)} and formulas for the density of the hyperbolic-cosine-type distribution [14], we can use the relation between the initial moments and derivatives of the characteristic function in order to obtain analytically values of improper integrals for a certain class of functions. For the parameters µ, β, m , the papers [15–17] present the general form of exact formulas for the integrals of expressions containing a beta function with complex-conjugate variable arguments. In particular, according to [16], values of the integrals of a combination of a power function, an exponential function, a hyperbolic secant or cosecant, and some polynomials with different parameters are obtained for m e N .

Table 2

Section { U ( n ; k ,0) } of the numerical prism

k n	1	2	3	4	5	6	7	8
1
2	1
3
4	2	3
5
6	16	30	15
7
8	272	588	420	105
9
10	7936	18960	16380	6300	945
11
12	353792	911328	893640	429660	103950	10395
13
14	22368256	61152000	65825760	36636600	11351340	1891890	135135
15
16	1903757312	5464904448	6327135360	3918554640	1427025600	310269960	37837800	2027025

Therefore, the integer set { U ( n ; k , j ) } introduced from probabilistic considerations is also of independent interest for mathematical analysis, number theory, coding theory, etc. A number of relations of the numerical prism and more detailed initial fragments of sections are presented in the author's monograph [17].