Cuckoo Search Algorithm for Stellar Population Analysis of Galaxies

Published Online October 2015 in MECS

Modern technology offers new good solutions for some problems, but still some automation problems that conventional computer systems simply cannot address. The limitations of using computers in solving such problems may rise from different aspects. Optimization is a process of searching for the optimal solutions to a particular problem of interest, and this search process can be carried out using multiple agents which basically form a system of progressing agents.

This system can progress by iterations according to a set of rules or mathematical equations. Subsequently, such a system will show some emergent characteristics, leading to self-organizing states which correspond to some optima in the search space. Once the self-organized states are reached, we say the system converges. Therefore, design of an efficient optimization algorithm is equivalent to mimicking the evolution of a selforganizing system [9].

Optimization concerns many disciplines with a wide range of applications. As time, money and resources are always limited, optimization is ever-increasingly more important. For example, energy-saving designs and green solutions to many industrial problems require a paradigm shift in thinking and design practice. On the other hand, people want smart and intelligent products, and computational intelligence has arose as a promising area with possibly wide ranging impact [9].

These days machine learning often uses optimization algorithms to enhance its learning performance, while optimization also borrows ideas from machine learning such as statistical learning theory and neural networks [9]. In this article, we will introduce cuckoo search as a powerful, nature-inspired metaheuristic algorithm for Stellar Population Analysis of Galaxies. In practically all applications in engineering and industry, we are always trying to optimize something whether to minimize the cost and energy consumption, or to maximize the profit, output, performance and efficiency [9].

The optimal use of available resources of any sort requires a paradigm shift in scientific thinking; this is because most real-world applications have far more complicated factors and parameters to affect the behavior of the system.

For any optimization problem, the integrated components of the optimization process are the optimization algorithm, an efficient numerical simulator and a realistic representation of the physical processes we wish to model and optimize [9, 14].

This is often a time-consuming process, and in many cases, the computational costs are usually very high. Once we have a good model, the overall computation costs are determined by the optimization algorithms used for search and the numerical solver used for simulation [9].

Optimization algorithms are the tools and techniques for solving optimization problems with an intention to find its optimality, though such optimality is not always reachable. This search for optimality is complicated further by the fact that uncertainty is almost always present in the real-world systems. Therefore, we seek not only the optimal design but also robust design in engineering and industry. Optimal solutions, which are not robust enough, are not practical in reality [9].

An algorithm can act like a tool to tune a complex system. If an algorithm does not use any state information of the problem, then the algorithm is more likely to be versatile to deal with many types of problem. However, such black-box approaches can also imply that the algorithm may not be efficient as it could be for a given type of problem. For example, if the optimization problem is convex, algorithms that use such convexity information will be more efficient than the ones that do not use such information. In order to be efficient to select states/solutions efficiently, the information from the search process should be used to enhance the search process [9].

Optimization algorithms focus on finding the optimal and practical solutions to complex problems under dynamic, complex loading pattern with complex nonlinear constraints. Different disciplines of science often benefits from the sharing of information one example of these are Genetic Algorithms[2], evolutionary algorithm [3-4] and differential evolution[5], animal behavior, such as particle swarm optimization[6], Tabu search [7], as well as physical annealing processes, such as simulated annealing [8]and Cuckoo Search [9].

The use of computer techniques for the analysis of astronomical data has been relatively frequent since the early nineties. Study stellar population of galaxies is very important because gives astrophysicists much information about their composition, ages and their evolution and frequently make use of large catalogues of information to test existing theories against, or to form new conjectures to explain the physical processes governing galaxies, star formation, and the nature of the universe.

The stellar populations of external galaxies have mixture of different ages, metal cities and chemical compositions, grouped into two types, Population I and population II and characterize different parts of galaxies. Population I stars are located in the disk singly and in galactic, or open star clusters. Population II stars were formed early in the history of the galaxy from pure hydrogen with an admixture of primordial helium. The most luminous population II stars are red giants, the number distribution of stellar populations present in a galaxy is a function of age [10].

Stellar populations of galaxies have been studied by analyzing the color magnitude diagrams and the integrated color of the galaxies [11-12, 1]. A first example of modeling stellar population is given by [13] to describing the evolution of the ( B-V ) color of the old open cluster M67. While a first example of modeling stellar population based on a Genetic algorithm is given by [1]. Also [14] predicted the spectral evolution of galaxies, in which stars a span wide range of ages and chemical compositions.

Many efforts have been made in recent years by many authors [15-22]. [20] assumed that the integrated light of the galaxies is coming from two kinds of stellar populations, population I and population II. They present an analytical method for deducing the relative contribution of the stellar populations in galaxies. In this paper we solve an optimization problem by evolving the best solution from an initial set of completely random guesses using cuckoo Search, the stellar population for four or three broad band color indices U-B, B-V, B-R and B-I of NGC 3384 and compare our results (ICS) with genetic algorithm [1].

The analysis based on the assumption that the integrated color of the galaxy results from a combination of two stellar populations with different metallic ties and different ages [1,20]. Our aim is to identify the relative contribution of these two populations and also their age in the galaxy.

This paper is organized as follows: the original cuckoo search algorithms briefly introduced in section 2. In section 3, the proposed algorithm is described, while the results are discussed in section 4. Finally, conclusions and future work are presented in last section.

• II.    The Original Cuckoo Search Algorithm

The Cuckoo search algorithm is a Meta heuristic search algorithm which has been proposed recently by Yang and Deb [9], it was based on the following idealized rules:

• •    Each cuckoo lays one egg at a time, and dumps it in a randomly chosen nest.

• •    The best nests with high quality of eggs (solutions) will carry over to the next generations.

• •    The number of available host nests is fixed, and a host can discover an alien egg with a probability p a e [ 0,1 ] .

Cuckoo search algorithm

Define Objective function f ( x ) , x = ( x ₁, x ₂, ..., x_d )

Initial a population of n host nests X i ( i = 1,2,..., d ) while (t < MaxGeneration) or (stop criterion);

Get a cuckoo (say i) randomly and generate a new solution by Lévy flights;

Evaluate its quality/fitness; Fi

Choose a nest among n (say j ) randomly;

if (F i > F j ),

Replace j by the new solution;

end

Abandon a fraction (P a ) of worse nests

[and build new ones at new locations via Lévy flights]; Keep the best solutions (or nests with quality solutions);

Rank the solutions and find the current best;

end while

Post process results and visualization;

End

• Fig.1. Pseudo code of cuckoo search algorithm

In this case, the host bird can either throw the egg away or abandon the nest so as to build a completely new nest in a new location [9]. Figure 1 illustrated the basic steps of CS algorithm

When generating new solutions x i (t + 1) for the i t cuckoo, the following Lévyflight is performed

x (t+1) = x (t) + a ® Levy(X)

Where a >  0 is the step size, which should be related to the scale of the problem of interest. The product Ф means entry-wise multiplications. We consider a Lévy flight in which the step-lengths are distributed according to the following probability distribution

Levyu = t -^ ,1 < X < 3 (2)

This has an infinite variance. Here the consecutive jumps/steps of a cuckoo essentially form a random walk process which obeys a power-law step length distribution with a heavy tail[23–27].

CS has been considered by many authors as a very successful algorithm, competing with other metaheuristics, such as PSO, Tabu Search (TS) and GA. In recent years, several investigations have been developed around CS, and been applied to various optimization problems in computer science, operations research, and engineering, among which are included: daily applications, computer science, electrical engineering, civil engineering, mechanical engineering, biomedical, economics, transport, ecology [9].

• III.    The Proposed Algorithm (Ics) for Stellar Population Analysis of Galaxies

Suppose that Optimization problem formulation for stellar population analysis of galaxies as published by[1,11,19,20] based on [14] model can be formulated as:

Where:

X ₀ = dex ( - 0.4 A ( U - B )₁ ) , X 1 = dex ( - 0.4 A ( B - V )_; ) ,

X 2 = dex ( - 0.4 A ( B - R ), ) , X ₃ = dex ( - 0.4 A ( B - 1 )J .

A = dex ( - 0.4 A ( U - B )_m ) , B = dex ( - 0.4 A ( B - V )_m ) ,

C = dex ( - 0.4 A ( B - R )_m ) , D = dex ( - 0.4 A ( B - 1 )_m ) .

The general form the observed color index is given by:

( B - X ) _m = ( B - Я ) II + 2.5log f l - P b + P b - 10 c ' E ' b - v * - 10 ^{( 0.4 A(} B ^{- X ) 1} )

For more detailed about problem formulation for stellar population analysis of galaxies see [1,11,14,19,20]. Figure 2 illustrated the steps of the proposed algorithm.

Cuckoo search algorithm for Stellar Population Analysis of Galaxies

Step 1: Define parameters CS, and input color index, U-B, B-V, B-R, B-I for observed color index m, reference values of populations I and reference values of Populations II;

Step2: For each color index U-B, B-V, B-R, B-I. Do;

Step3: Get cuckoo (say i) randomly for each observed color index m, populations I and populations II; e.g. (U-B) m , (U-B) I , (U-B) II ;

Step 4: Calculate β via equation (6);

Step 5: If β satisfy the constraint (3) go to step 6 else go to step 3;

Step 6: Evaluate its quality/fitness;

Step 7: Choose a nest among each type (say j) randomly;

Step 8: if (f^ ), >(fzk +1 1), where k is the size of

Minimize f ( P ) =-----

1 + ^P

	1-Л
subject to g 1 :	P --= 0; 1 - X 0
	„  1 - B
g 2 :	p  ,  „   = 0;
	1 - X 1            (3)
	i-c
g 3 :	P --= 0; 1 - X 2
g 4 :	P - 1 = 0;
	1 - X 3

each population, z type color;

Step 9: Replace j by the new solution;

Step 10: Keep the best solutions for each population (or stellar with quality solutions);

Step 11: Rank the solutions and find the current best for each population;

Step 12: Repeat Steps 3–11 until definite termination conditions are met;

Step 13: Repeat steps 2- 12 for each color index until definite termination conditions are met;

Step 14: Keep the best solutions;

Step 15: Post process results and visualization.

Fig.2. Pseudo code of cuckoo search algorithm for Stellar Population Analysis of Galaxies

• IV.    Numerical Results and Discussion

  The analyses observational data for NGC 3384 case II [1] using as an age reference line the models, of [14] are employed in this paper. Where n is the iteration number.

All experiments were performed on a Windows 7 Ultimate 64-bit operating system; processor Intel Core i5 760 running at 2.81 GHz; 4 GB of RAM and code was implemented in MATLAB.

At the same time, the global optimization capability and the computational efficiency of Cuckoo Search algorithm result in genetic algorithm results are compared to expose Cuckoo Search algorithm work well as the genetic algorithm in the field of space science.

Our rustles of NGC 3384 to test the result of Cuckoo Search with genetic algorithm,[1]with the same condition and the same of initial values of Population I and Population II is very good agreement; to tell that a dominated population in NGC 3384 is the old stellar population with age > 5Gyr have been found, see Fig. 3.

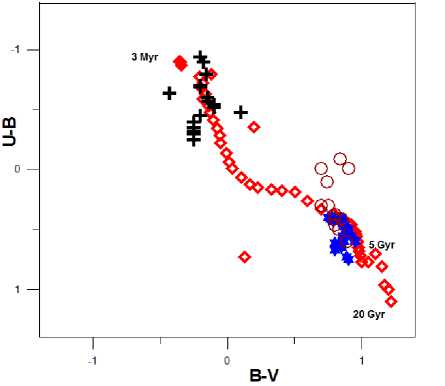
Fig.3. Color of young (crosses), old (open circles) population and the total observed color of the test points (stars) in comparison with that from the Bressan model[14] (dots).

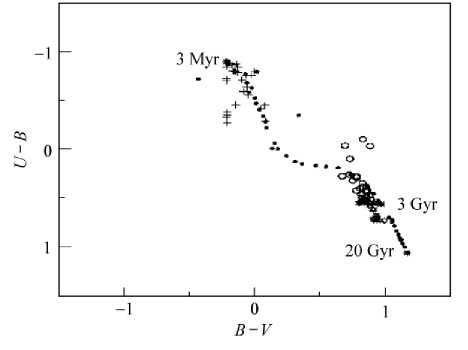
Fig.4. Color of young (crosses), old (open circles) population and the total observed color of the test points (stars) in comparison with that from the Bressan model (dots)[14]. this figure taken from [1].

In Fig. 3 presents the distribution of the color indices of the test points as well as that of the calculated color indices for both young and old population in color-color diagram, in comparison with that from the population synthesis model [14].

The figure shows that the color of Population II has the same location as the observed color. The contribution of the young population (βb with age less than 105 yr) to the total intensity is small: from 0.12 to 0.31 with the variation in the standard deviation (σβ_) as a function of accurse of βb range from 0.007 to 0.03. While in Attia et al (2005) the contribution of the young population (age less than 105 yr) to the total intensity is 0.1≤ βb ≤0.4 and dominated population in NGC 3384 is the old stellar population with age > 5Gyr, see above Fig. 4, presents the distribution of the color indices of the test points as well as that of the calculated colorindices for both young and old population in color-color diagram, in comparison with that from the population syntheses model[14]. The figure shows that the color of Population II (old) has the same location as the observed color.

Fig. 4 shows the effectiveness of approach for optimizing the model parameters and variation in the standard deviation (σβ_) as a function of the iteration number.

• V.    Conclusions and Future Work

This paper introduced an improved cuckoo search Algorithm for stellar population analysis of galaxies. Several simulation examples show that the algorithm can converge to be the best solution, and it has a high convergence rate and high accuracy.

The proposed algorithm has been provided the better and clear way to determine the age and relative contribution of different stellar populations.

The results proved the superiority of the proposed methodology. The good result of a cuckoo search algorithm confirms that the convergence rate of the different discipline interesting (i.e. for determining the age and relative contribution of different stellar populations in galaxies as a comparison with paper [1] of genetic algorithm for the same examples).

Cuckoo search algorithm proposed successfully be applied to a wide range of optimization because it found better solutions in comparison with the solutions obtained by numerical studies and solve performed well in several complicated problems. Future work includes another direction can be the study of different mechanisms for adapting the β parameter for population I, population II and population III. Finally, the idea to select cuckoo search algorithm for analysis stellar population of galaxies can be extended to the other stellar system.

Acknowledgements

The authors would like to acknowledge the invaluable contribution of Dr. Norman Gray, School of Physics and Astronomy , University of Glasgow, Glasgow, UK for his helpful comments.